
Boyarshinov_ChM_T3
.pdf
Нормированное пространство X вложено в нормированное пространство Xˆ , если всюду на X задана линейная функция J(x), причем существует
постоянная > 0 такая, что 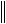 J x
J x 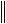
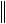 x
x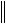 x X .
x X .
Прямой суммой двух линейных пространств Z = X + Y и называется совокупность пар z = (x, y), для которых операции сложения пар и умножения пары на число определяются следующим образом: если z1 = (x1, y1), а z2 = (x2, y2)
и 1, 2 – скаляры, то 1z1 2z2 1x1 2x2, 1y1 2 y2 .
Линейное многообразие L, лежащее в нормированном пространстве E
L E , называется плотным в E, если x E, |
0 |
найдется элемент u L |
такой, что x u . |
|
|
Нормированное пространство называется полным, если в нем всякая фундаментальная последовательность сходится. Полное нормированное пространство называется банаховым.
Пусть X – банахово пространство, а R – вещественная ось, L X,R – банахово пространство линейных ограниченных функционалов, заданных на X.
Это пространство называется сопряженным к X и обозначается |
X* L X,R . |
|||||||||||||
Значение линейного функционала |
f X* |
на x X обозначается |
x, f . |
|||||||||||
Пусть xn X . |
Последовательность |
xn называется слабо сходящейся к |
||||||||||||
элементу x |
|
X , если xn, f |
|
x, f |
|
X |
* |
. Если |
x |
n |
x |
слабо, то x |
||
|
|
|
f |
|
|
|
||||||||
называется слабым пределом xn . В отличие от слабо сходящихся, последовательности, сходящиеся по норме пространства X называются сильно сходящимися.
Множество M банахова пространства X называется слабо компактным, если из любой (бесконечной) последовательности его элементов можно выбрать слабо фундаментальную (в смысле слабой сходимости) последовательность.
Нормированное пространство X называется сепарабельным, если в нем существует счетное, плотное в X множество.
Пространство H со скалярным произведением называется гильбертовым, если оно полно в смысле сходимости по норме, порожденной скалярным произведением.
Пусть в гильбертовом пространстве H задано подпространство M. Согласно теореме Рисса1 каждому x H можно поставить в соответствие
1 Рисс Фридьеш [22.1.1880 – 28.2.1956] – венгерский математик. Учился в Цюрихе
(1897-1899), Будапеште (1899-1901), Геттингене и Париже (1903-1904). В 1916 году стал членом Венгерской академии наук. Профессор университетов в Клуже (1912-1919), Сегеде (1920-1945), Будапеште (с 1946). Основные труды опубликовал по функциональному анализу. Изучал векторные пространства, исследовал системы линейных уравнений с бесконечным числом неизвестных, один из основателей теории топологических
21

единственный элемент y M – ортогональную проекцию x на M. Тем самым в H определен оператор ортогонального проектирования (для краткости –
проектор) y Px.
Пространство ~1 , состоит из всевозможных функций ( ), непрерывно
H a b u x
дифференцируемых на [a, b], со скалярным произведением
b b
u,v u x v x dx u x v x dx
aa
инормой, соответствующей этому скалярному произведению,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
b |
|
|
1 2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
u u2 x dx u 2 x dx . |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
H1 a,b |
является пополнением H~1 a,b в этой норме. Элементами H1 a,b |
||||||||||||||||||||||||||
являются классы, состоящие из последовательностей |
|
|
|
~1 |
a,b , |
|||||||||||||||||||||||
um x H |
||||||||||||||||||||||||||||
фундаментальных в H~1 a,b в среднем, то есть таких, что |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
b |
|
|
x u |
|
x 2 dx |
b |
|
|
x u |
x 2 dx 0 |
|
|
|
|
|||||||||
|
|
|
|
|
|
u |
m |
n |
|
u |
. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
n |
|
|
m,n |
|
|
|
|
||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из условия фундаментальности в среднем um x в H~1 a,b следует, что |
|||||||||||||||||||||||||||
по отдельности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
b |
|
|
x u |
|
x 2 dx 0 |
|
b |
u x u |
x 2 dx 0 |
|
|
|||||||||||||||
|
|
|
u |
m |
n |
, |
|
. |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
m,n |
|
|
|
m |
|
n |
|
m,n |
|
|
||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
Согласно определению |
[] пространства |
L2 a,b существуют |
функции |
||||||||||||||||||||||||
u x L2 a,b и w x L2 a,b такие, что |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
u |
m |
x |
u x , |
u |
x w x |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
m |
|
|
m |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
~1 |
a,b , тогда в |
L |
2 |
a,b |
определены элемент u(x) с |
||||||||||||
в среднем. Пусть um x |
|
H |
|
|
||||||||||||||||||||||||
представителем um x и элемент w(x) |
с представителем um x . Элемент w(x) |
|||||||||||||||||||||||||||
называется обобщенной производной (в смысле Соболева) от u(x). |
|
|
|
|||||||||||||||||||||||||
|
Пространство |
|
|
|
|
° |
a,b |
является |
|
пополнением |
|
в |
метрике |
|||||||||||||||
|
|
|
|
|
H1 |
|
|
|||||||||||||||||||||
u 2° |
|
|
bu 2 x dx |
|
линейного пространства непрерывно дифференцируемых |
|||||||||||||||||||||||
H |
1 a,b |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пространств.
Теорема Ф. Рисса [18]: пусть H – гильбертово пространство. Для любого линейного ограниченного функционала f, заданного повсюду на H, существует единственный элемент
y H такой, что x H |
x, f x, y , при этом |
f y . |
22

функций, принимающих на границе значения, равные нулю. |
° |
1 a,b является |
|||
H |
|||||
гильбертовым |
пространством |
со |
скалярным |
|
произведением |
b |
|
|
|
|
|
u,v a u x v x dx. |
|
|
|
|
|
Обобщенное решение дифференциального уравнения |
|
|
|||
Рассматривается уравнение |
|
|
|
|
|
|
Ax y, |
|
|
|
(1.19) |
где A – линейный оператор, действующий из плотной в вещественном гильбертовом пространстве X области определения D(A) в то же самое пространство X. Скалярное произведение в X обозначается через (x, y), а соответствующая ему норма – через  x
x . H – еще одно гильбертово пространство со скалярным произведением [x, y] и нормой ||| x|||, соответствующей этому скалярному произведению. Пусть выполнены следующие условия.
. H – еще одно гильбертово пространство со скалярным произведением [x, y] и нормой ||| x|||, соответствующей этому скалярному произведению. Пусть выполнены следующие условия.
I.H вложено в X, H D A , причем в H + H определен билинейный ограниченный функционал a(x, y), то есть вещественнозначная функция, линейная по u при фиксированном v, линейная по v при фиксированном u, такая, что
a u,v c|||u ||| |||v|||, |
(1.20) |
при этом x D A и v H |
|
a x,v Ax,v . |
(1.21) |
II. Найдется постоянная 0 такая, что u H выполняется неравенство
a u,v |||u |||2 . |
(1.22) |
Оператор, удовлетворяющий условиям I и II, называется H-эллиптическим. x H – обобщенное решение уравнения (1.19) с H-эллиптическим оператором A, если имеет место тождество
a x,v y,v . |
(1.23) |
Для доказательства существования и единственности обобщенного решения уравнения (1.19) используется метод Галеркина. В H выбирается координатная система i , i 1, . Пусть Pm – проектор H на линейное подпространство Hm, натянутое на первые m векторов этой системы. Элемент xm Hm называется галеркинским приближением обобщенного решения уравнения (1.19), если vm Hm имеет место тождество
a xm,vm y,vm . |
(1.24) |
Лемма 1.1. Решение задачи (1.24) имеет вид
23
m |
|
xm bi i , |
(1.25) |
i 1 |
|
где коэффициенты bi, i 1,m определяются решением системы m линейных уравнений с m неизвестными,
m |
bi |
y, j , |
|
|
a i , j |
j 1,m. |
(1.26) |
i 1
Доказательство. Элемент xm принадлежит Hm и, значит, имеет вид (1.25). При подстановке в (1.24) представления (1.25) и выражения
m |
|
vm cj j , |
(1.27) |
j 1
всилу билинейности a(u, v) и линейности скалярного произведения получается
m |
bicj |
m |
cj . |
|
a i, j |
y, j |
(1.28) |
||
i, j 1 |
|
j 1 |
|
|
Но vm Hm произвольно, |
то есть |
cj , j 1,m |
в (1.27) и (1.28) – |
|
произвольные постоянные. Следовательно, (1.24) и (1.28) эквивалентны, что и доказывает лемму.
Лемма 1.2. Пусть оператор A является H-эллиптичным. Тогда для всякого m существует единственное галеркинское приближение xm обобщенного решения уравнения (1.19).
Доказательство. Воспользуемся условием II. Если a xm,vm 0 vm Hm , то это верно и при vm xm . Но тогда, в соответствии с (1.22),
0 a xm,xm ||| xm |||2,
откуда следует, что xm = 0. Поскольку однородная задача, получающаяся из (1.24) при y = 0, имеет лишь тривиальное решение, то задача (1.26), а вместе с ней и (1.24) будут однозначно разрешимы.
|
|
Лемма 1.3. Если |
u |
m |
u |
0 |
слабо в H, а |
v |
m |
v |
0 |
сильно в H, то |
|||||||||||
a u |
|
|
|
m |
|
m |
|||||||||||||||||
m |
,v |
m |
a u |
0 |
,v |
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Вследствие билинейности |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
a um,vm a u0,v0 a um,vm v0 a um u0,v0 . |
|
(1.29) |
|||||||||||||||||
|
|
Так как последовательность um сходится слабо, то, согласно [], она |
|||||||||||||||||||||
ограничена. Поэтому из неравенства (1.20) следует |
|
|
|
|
|||||||||||||||||||
|
|
|
|
a u |
m |
,v |
m |
v |
0 |
c|||u |
m |
||| |||v |
m |
v |
0 |
||| |
0. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
||||||
24

Поскольку v0 фиксировано, u H выражение a u,v0 определяет в H линейный ограниченный функционал. Но тогда, по теореме Рисса, найдется w0 H такой, что a u,v0 u,w0 u H . Согласно определению слабой сходимости um
|
|
|
|
a u |
m |
u |
0 |
,v |
0 |
u |
m |
u |
0 |
,w 0. |
||||
|
|
|
|
|
|
|
|
|
|
0 |
m |
|||||||
В (1.29) оба слагаемых в правой части равенства стремятся к нулю, что и |
||||||||||||||||||
доказывает утверждение леммы. |
|
|
|
|
|
|
|
|||||||||||
Теорема 1.1. Пусть пространство H сепарабельно и оператор A является |
||||||||||||||||||
H-эллиптичным, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1) |
для всякого m галеркинское приближение xm обобщенного решения |
|||||||||||||||||
|
уравнения (1.19) существует и единственно; |
|||||||||||||||||
2) |
обобщенное решение уравнения (1.19) существует и единственно; |
|||||||||||||||||
3) |
x |
m |
x |
0 слабо; при этом справедлива оценка |
||||||||||||||
|
m |
|||||||||||||||||
|
|
|
|
||| x |
m |
x |
0 |
||| c 1 |
||| P x x|||. |
(1.30) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||
Доказательство. Утверждение 1) теоремы верно в силу леммы 1.2. Для доказательства утверждения 2) используется сепарабельность пространства H.
Пусть, |
как |
и ранее, |
i , i 1, |
– ортонормированный базис в H. |
v H |
P v v, |
то есть ряд |
Фурье, составленный для элемента v, |
|
|
m |
m |
|
|
сходится к v. Рассматривается последовательность галеркинских приближений
xm . Полагая |
в (1.24) |
vm xm |
и пользуясь |
неравенством (1.22), можно |
|
получить |
|
|
|
|
|
|
|
||| |
xm |||2 a xm,xm y,xm |
y xm . |
|
|
Но H вложено в X, и поскольку xm H , то найдется постоянная k > 0 такая, |
||||
что |
xm k ||| xm ||| при m = 1, 2, … |
|
|
||
|
Следовательно, |
|
|
|
|
|
|
|
||| xm |||2 k ||| xm ||| y , |
||
откуда |
|
|
|
|
|
|
|
|
||| xm ||| k 1 y . |
|
|
|
Значит, последовательность галеркинских приближений xm ограничена в |
||||
H, |
и тогда она |
слабо компактна. |
Пусть xm |
– ее подпоследовательность, |
|
сходящаяся в H слабо к некоторому элементу x0 H . Фиксируя произвольный
элемент v H , в соответствии с (1.24), |
получаем, что a xm ,Pm v y,Pm v . При |
||||||||
этом |
P |
v v |
сильно, а |
x |
m |
x |
0 |
слабо. По лемме 1.3 и свойству |
|
m |
|
|
|
|
|||||
|
|
m |
|
|
|
m |
|
|
|
25
непрерывности скалярного произведения имеет место a x0,v y,v . Из произвольности v H следует, что x0 – обобщенное решение уравнения (1.19).
Пусть x0, x0 |
– два обобщенных решения. Для произвольного v H |
|
|
a x0,v y,v , |
a x0,v y,v . |
Вычитание второго тождества из первого дает выражение a x0 x0,v 0. Полагая v x0 x0 и используя (1.22), находим
|
0 a x0 x0,x0 x0 ||| x0 x0 |||2 , |
и, следовательно, x0 |
x0. |
Полагая в (1.23) |
v vm и вычитая его из (1.24), получаем |
|
a xm x,vm 0 vm Hm . |
В частности, a xm x,xm a xm x,Pmx 0. Но тогда по условию II |
|
||| |
xm x|||2 a xm x,xm x a xm x,x |
a xm x,Pmx x c||| xm x||| ||| Pmx x|||. |
|
Отсюда следует оценка (1.30). |
|
Сходимость метода конечных элементов |
|
Рассматривается дифференциальное уравнение |
|
|
(1.31) |
g t x c t x y t , |
|
с граничными условиями |
|
x 0 x 1 0. |
(1.32) |
Коэффициент a(t) считается непрерывно дифференцируемым на [0, 1], а коэффициенты c(t) и y(t) – непрерывными на [0, 1]. Пусть на отрезке [0, 1]
|
g t 0, |
c t 0. |
|
(1.33) |
|
Обобщенным решением задачи (1.31) |
– (1.32) называется |
функция |
|||
° |
1 0,1 , удовлетворяющая тождеству (1.23) для всех |
° |
1 0,1 , где в |
||
x t H |
v t H |
||||
данном случае |
|
|
|
|
|
|
1 |
|
1 |
|
|
|
a x,v g t x t v t dt |
c t x t v t dt , |
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
1
y,v y t v t dt .
0
26
Иными словами, тождество (1.23) получается в результате скалярного умножения в L2 0,1 уравнения (1.31) на произвольную функцию v t H° 1 0,1 и
интегрирования по частям. Это позволяет понизить требования гладкости к функции x(t), одновременно повысив требования дифференцируемости
°
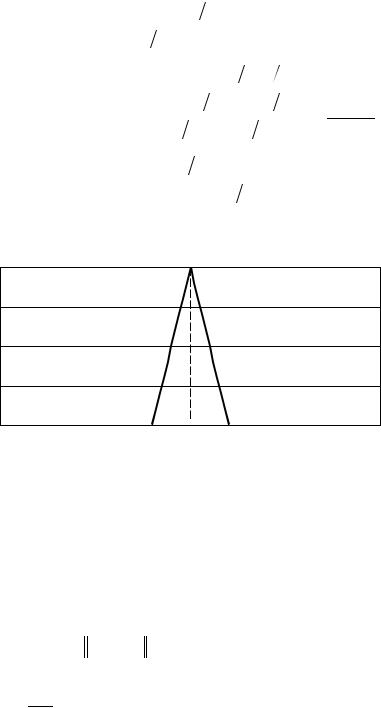
функции v(t). В качестве координатной системы в Hm H1 0,1 выбирается система функций (рис. 1.7)
|
1 mt, t 0,1 m , |
|
||
0 t |
t 1 m,1 ; |
|
||
|
0, |
|
||
|
|
|
|
|
|
1 i mt, |
t i 1 m,i m , |
||
t |
1 i mt, |
t i m, i 1 m , |
||
i |
|
t i 1 m, i 1 m , |
|
|
|
0, |
i 1,m 1; |
||
|
|
|
|
|
|
0, |
t 0,1 1 m , |
|
|
m t |
|
t 1 1 m,1 . |
|
|
|
n 1 mt, |
|
||
1
0,75
0,5
0,25
0 







































 (i-1)/n i/n (i+1)/n
(i-1)/n i/n (i+1)/n
Рис. 1.7. Вид функции i координатной системы
Для задачи (1.31) – (1.32) показано [], что ее обобщенное решение в действительности принадлежит C2 0,1 . Там же получена оценка,
показывающая, что для всякой функции x t H2 0,1 при m
1 x Pmx H1 0,1 O m ,
где Pm – проектор в H1(0, 1) на подпространство кусочно-линейных функций, натянутое на i , i 1,m. Таким образом, из оценки теоремы 1.1 следует сходимость галеркинских аппроксимаций xm к точному решению задачи.
27
Контрольные вопросы и задания
Сформулируйте идею метода взвешенных невязок
Сформулируйте требования к пробным функциям, используемым в методе взвешенных невязок, и обоснуйте их необходимость
Сформулируйте требования к взвешивающим функциям, используемым в методе взвешенных невязок, и обоснуйте их необходимость
Какой смысл вкладывается в название слабая формулировка задачи?
Что представляет собой слабое решение задачи?
Какой смысл вкладывается в название обратная формулировка задачи?
При каком условии метод взвешивающих невязок приводит к поиску решения дифференциальной задачи только на границе?
Приведите классификацию методы взвешенных невязок.
При каких условиях метод моментов оказывается частным случаем метода взвешенных невязок?
При каких условиях метод Галеркина оказывается частным случаем метода взвешенных невязок?
При каких условиях метод наименьших квадратов оказывается частным случаем метода взвешенных невязок?
При каких условиях метод коллокаций оказывается частным случаем метода взвешенных невязок?
При каких условиях метод подобластей оказывается частным случаем метода взвешенных невязок?
При каких условиях метод конечных разностей оказывается частным случаем метода взвешенных невязок?
28

2 . А П П Р О К С И М А Ц И Я Ф У Н К Ц И Й
В классе методов, объединенных названием методы взвешенных невязок, применяются специальные процедуры аппроксимации функций, основанные на разложении в ряды по системам кусочно-гладких функций.
Функции одной переменной
Первоначально рассматриваются способы и алгоритмы аппроксимации функций с помощью кусочно-постоянных, кусочно-линейных и кусочноквадратичных функций.
Кусочно-постоянные функции
Для определенности рассмотрим аппроксимацию функции f x x2 на
отрезке G = [0, 1]. Представим этот отрезок объединением G G1 G2 |
G3 G4 , |
|||||||||||||||||||||
где G1 0,1 |
4 , G2 |
1 4,1 2 , |
G3 1 2,3 4 , G4 |
3 4,1 . На каждом из этих |
||||||||||||||||||
интервалов (рис. 2.0) определим кусочно-постоянные пробные функции |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1, |
x Gi , |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
i x |
x Gi. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
1(x) |
|
|
|
|
1 |
|
|
|
|
|
|
2(x) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
||||
0 |
0,25 |
0,5 |
0,75 |
0 |
0,25 |
0,5 |
0,75 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
3(x) |
|
|
|
|
1 |
|
|
|
|
|
|
4(x) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
||||
0 |
0,25 |
0,5 |
0,75 |
0 |
0,25 |
0,5 |
0,75 |
|||||||||||||||
|
|
|
Рис. 2.0. Пробные кусочно-постоянные функции |
|
|
|
|
|||||||||||||||
Представим заданную функцию f(x) в виде разложения |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x fm x ai i x , |
|
|
|
|
|
|
(2.0) |
|||||||||
i 1
29

причем в рассматриваемом случае, очевидно, m = 4. Взвесим погрешность
m
f x ai i x
i 1
представления функции в области G, используя в качестве взвешивающих те же самые функции k,
1 |
|
m |
|
1 |
1 |
m |
k 1,m. |
|
|
|
|
|
|||
f ai |
i kdx f kdx k ai idx, |
||||||
0 |
|
i 1 |
|
0 |
0 |
i 1 |
|
Потребуем равенства нулю всех взвешенных на рассматриваемом отрезке погрешностей,
1 |
m |
1 |
|
|
f kdx ai i kdx 0, |
k 1,m. |
(2.1) |
||
0 |
i 1 |
0 |
|
|
Эти равенства представляют собой систему четырех линейных алгебраических уравнений относительно четырех искомых коэффициентов ai , i 1,4 разложения (2.0). В соответствии с выражением (2.1) подсчитаем значения интегралов
1 1 4 1 1 1
4 1 1 1
1 1dx = 1dx =1 4, |
2 1dx 3 1dx 4 1dx 0, |
||||
0 |
0 |
0 |
|
0 |
0 |
|
1 |
1 4 |
|
3 1 4 |
|
|
f 1dx x2dx x |
|
1192. |
||
|
0 |
0 |
3 0 |
|
|
Аналогично вычисляются остальные интегралы. Подстановка их значений в выражение (2.1) приводит к системе четырех линейных алгебраических уравнений
a1 |
|
4 0a2 0a3 |
0a4 |
1192, |
||||||
|
|
|
|
4 0a |
|
0a |
|
7 192, |
||
0a a |
2 |
3 |
4 |
|||||||
|
1 |
|
|
|
|
|
(2.2) |
|||
|
|
0a2 |
a3 |
4 0a4 |
||||||
0a1 |
19 192, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0a2 |
0a3 |
|
a4 |
4 37 192. |
||||
0a1 |
|
|||||||||
Искомые коэффициенты разложения равны |
||||||||||
a1 1 48, |
a2 7 |
48, |
a3 19 |
48, a4 37 48. |
||||||
Аппроксимация функции f x x2 |
на отрезке [0, 1] с помощью |
|||||||||
представления (2.0) показана на рис. 2.1.
30
