
Boyarshinov_ChM_T3
.pdf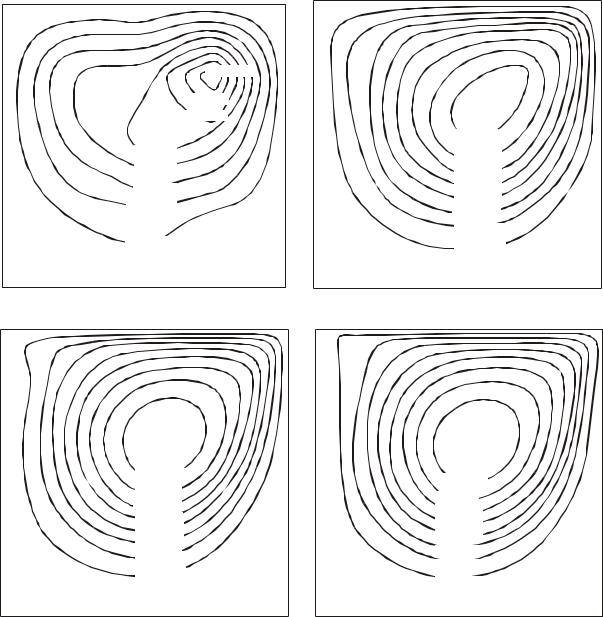
Рис. 5.2. Сетка конечных элементов, аппроксимирующая замкнутую полость.
На рис. 5.2 показана сетка конечных элементов с нанесенными номерами узлов и треугольных элементов, аппроксимирующая замкнутую полость, занятую жидкостью.
На рис. 5.3 представлены результаты вычисления функции тока на сетках с увеличивающимся числом конечных элементов (структура сетки показана на рис. 5.2), число Рейнольдса Re = 400, шаг интегрирования по времени t = 0,01. Результаты вычислительного эксперимента показывают, что уже при числе элементов, равном 512 и 2048, различие решений незначительно.
-0,075 |
-0,065 |
-0,055 |
-0,045 |
-0,035 |
-0,025 |
-0,015 |
-0,005 |
а |
-0,085 |
-0,075 |
-0,065 |
-0,055 |
-0,045 |
-0,035 |
-0,025 |
-0,015 |
в |
-0,055 |
-0,065 |
-0,055 |
-0,045 |
-0,035 |
-0,025 |
-0,015 |
-0,005 |
б |
-0,085 |
-0,075 |
-0,065 |
-0,055 |
-0,045 |
-0,035 |
-0,025 |
-0,015 |
г |
111 |
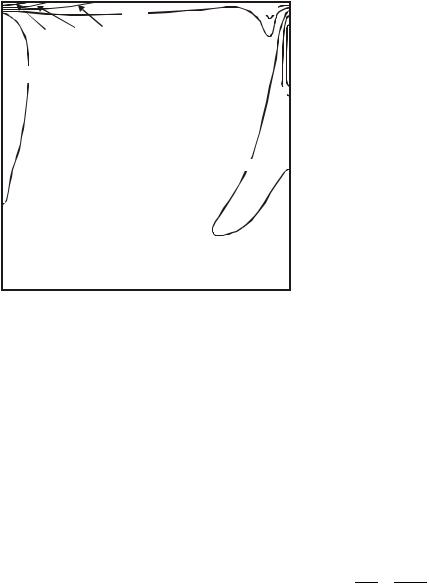
Рис. 5.3. Функции тока, полученные при расчетах на сетках с числом конечных элементов, равным 32 (а), 128 (б), 512 (в) и 2048 (г)
На рис. 5.4 представлено поле функции завихренности , полученное при расчетах с использованием сетки из 2048 конечных элементов.
-10 |
-20 |
|
|
-40 -30-20 |
|
|
|
0 |
|
Рис. 5.4. Функции завихренности, |
|
10 |
полученные при расчетах на сетке с |
||
|
2048 конечными элементами
0
Контрольные вопросы и задания |
|
Поясните физический смысл слагаемого |
v qd , получающегося при |
|
p |
выводе разрешающих соотношений для определения функции тока. Как повлияет его присутствие на выполнение процедуры ансамблирования конечных элементов?
Установите вид матрицы Vp в выражении (5.11). Как выполнять вычисления этого слагаемого?
1 |
|
Поясните физический смысл слагаемого Re |
nm qd , получающегося при |
p |
|
выводе разрешающих соотношений для определения функции завихренности. Как повлияет его присутствие на выполнение процедуры ансамблирования конечных элементов?
Установите вид матрицы Wp в выражении (5.12). Как выполнять вычисления этого слагаемого?
При каких способах аппроксимации решений m, m в пределах конечных элементов возможно нахождение поля давления P при использовании соотношений (5.13)?
112
113
6 . М Е Т О Д Г Р А Н И Ч Н Ы Х Э Л Е М Е Н Т О В
Вернемся к уравнению Пуассона (1.0) с граничными условиями (1.1) и (1.2). Его решение um, как и ранее, разыскивается в виде (1.3). Обратная формулировка этой задачи (1.9)
k |
um |
d Q kd U |
k |
d um |
k |
d um |
kd f kd 0 |
|
n |
n |
n |
||||||
U |
|
Q |
U |
|
Q |
|
|
|
получена взвешиванием невязок уравнения (1.0) и граничных условий (1.1), (1.2) по всей области и границам Q и U, соответственно. Если все взвешивающие функции k удовлетворяют уравнению Лапласа
k 0, |
k 1,m, |
(6.0) |
из предыдущего выражения следует соотношение (1.10) для значений искомой функции um и ее производной um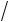 n на границах Q и U,
n на границах Q и U,
k |
um d um |
k d U k d Q kd f kd , |
k 1,m. |
|||||
U |
n |
Q |
n |
U |
n |
Q |
|
|
|
|
|
|
|||||
Пример 6.1 (из книги []). Рассматривается дифференциальное уравнение |
||||||||
|
|
|
|
u u x 0 |
|
|
||
с граничными условиями u 0 0, |
|
|
|
|
||||
u 1 0. |
|
|
|
|||||
С помощью функции w взвешиваются невязки дифференциального уравнения, получаемые на приближенном решении u~, удовлетворяющем заданным граничным условиям:
1
u~ u~ x wdx 0.
0
Первое слагаемое под знаком интеграла преобразуется по частям,
1 |
|
1 |
|
|
1 |
|
|
~ |
|
|
1 |
|
|
~ |
|
~ |
|
~ |
|
|
|
1 |
~ |
|
|
||
u wdx u w |
dx u w dx u w0 |
u w dx |
|||||||||||
0 |
|
0 |
|
|
0 |
|
|
|
|
|
0 |
|
|
~ |
|
1 |
1 |
~ |
|
1 |
~ |
|
~ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
u w0 |
uw |
dx uw dx |
u w0 |
|||||||||
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
1
u~w 10 u~w dx
10 u~w dx
0
1
u~ 1 w 1 u~ 0 w 0 u~ 1 w 1 u~ 0 w 0 u~w dx
0
|
|
|
|
|
1 |
|
|
|
u~ 0 w 0 u~ 1 w 1 u~w dx. |
||||
|
|
|
|
|
0 |
|
Здесь учтено, что в силу заданных граничных условий |
||||||
|
|
u~ 0 w 0 0, |
u~ 1 w1 0. |
|||
Подстановка полученного соотношения в интегральное уравнение |
||||||
приводит к выражению |
|
|
|
|
|
|
1 |
|
~ |
|
|
1 |
1 |
~ |
|
~ |
|
~ |
||
uw dx |
u 0 w 0 u 1 w 1 |
uwdx xwdx |
||||
0 |
|
|
|
|
0 |
0 |
1 |
|
~ |
|
|
|
1 |
~ |
|
|
~ |
|
1 xwdx 0. |
|
u |
w |
w dx u |
0 w 0 u |
1 w |
||
0 |
|
|
|
|
|
0 |
Пусть пробная взвешивающая функция w удовлетворяет уравнению |
||||||
|
|
|
|
|
|
|
|
|
|
w w 0, |
|
||
тогда интегральное выражение преобразуется к более простому виду |
||||||
|
|
1 |
|
|
|
|
|
|
xwdx u~ 0 w 0 u~ 1 w 1 . |
||||
|
|
0 |
|
|
|
|
Это соотношение является линейным алгебраическим уравнением относительно значений u~ 0 и u~ 1 (на левом конце задано значение функции u, на правом конце – значение производной u ).
Решением дифференциального уравнения w w 0 является функция
w Asin x Bcos x ,
где А и В – константы интегрирования. Подстановка этой функции приводит к выражению
1
x Asin x Bcos x dx u~ 0 Asin 0 Bcos 0 u~ 1 Acos 1 Bsin 1 .
0
В силу независимости коэффициентов А и В приходим к системе двух алгебраических уравнений относительно искомых значений u~ 0 и u~ 1 ,
1 xsin x dx u~ 1 cos 1 ,
01
xcos x dx u~ 0 u~ 1 sin 1 .
0
Поскольку
115

1 |
1 |
xsin x dx sin 1 cos 1 , |
xcos x dx cos 1 sin 1 1, |
0 |
0 |
решением задачи являются значения
u~ 1 tg 1 , u~ 0 1 cos 1 . cos 1
В результате получены значения искомой функции u~ 1 и ее производной u~ 0 на концах рассматриваемого отрезка без непосредственного решения исходного дифференциального уравнения.
Фундаментальное решение
Обратимся к уравнению (6.0). Потребуем, чтобы взвешивающие функции удовлетворяли уравнению1
k x xk , |
(6.1) |
где (x – xk) – дельта-функция Дирака, xk – точка, где -функция обращается в бесконечность. Выражение (1.10) преобразуется к виду
um xk U |
k |
d k |
um |
d um |
k |
d Q kd f kd . (6.2) |
|
n |
n |
n |
|||||
U |
|
U |
|
Q |
|
Q |
|
Это соотношение позволяет определить значение um искомой функции в точке xk внутри области , поскольку все величины, входящие в подынтегральные выражения, стоящие в правой части, либо заданы граничными условиями, либо уже найдены из решения уравнения (1.10).
Пример 6.2. Для рассмотренной выше задачи из примера 6.1 необходимо построить фундаментальное решение и определить значение искомой функции для точки xk, лежащей внутри рассматриваемого отрезка [0, 1]. Фундаментальным решением для этой задачи является функция, удовлетворяющая уравнению
w w x xk .
Убедимся, что функция |
|
|
|
|
|
|||
w |
1 |
sin r , |
r |
|
x xi |
|
. |
|
|
|
|||||||
|
||||||||
2 |
|
|
|
|
|
|
||
является искомым фундаментальным решением.
1 Решение уравнения (6.1) называется фундаментальным.
116

Пусть x > xk. В этом случае r = x – xk. Дифференцирование дает
|
|
1 |
cos r r |
|
|
1 |
cos r |
, |
|
|
|
1 |
sin r r |
|
|
1 |
sin r . |
||
w |
2 |
|
2 |
w |
2 |
|
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставка этих значений в уравнение приводит к выражению |
|||||||||||||||||||
|
|
|
|
w |
1 |
sin r |
1 |
sin r 0. |
|
|
|||||||||
|
|
|
w |
|
2 |
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пусть x < xk. В этом случае r = xk – x. Аналогично предыдущему случаю |
|||||||||||||||||||
определяются производные, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
cos r r |
|
|
1 |
cos r , |
|
|
|
1 |
sin r r |
|
|
1 |
sin r . |
|||
w |
2 |
|
2 |
w |
|
2 |
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подстановка этих значений в проверяемое уравнение дает |
|||||||||||||||||||
|
|
|
|
w |
1 |
sin r |
1 |
sin r 0. |
|
|
|||||||||
|
|
|
w |
|
2 |
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пусть x = xk. Теперь r = |
0, w и, |
следовательно, дифференциальное |
|||||||||||||||||
уравнение терпит разрыв в рассматриваемой точке. Для проверки выполнения условий, накладываемых на –функцию, выполняется интегрирование дифференциального уравнения,
1 |
|
|
|
|
|
1 |
|
|
|
1 |
wdx |
1 |
|
1 |
1 |
sin x xk dx |
|
w w dx |
|
w dx |
|
w |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
0 |
|
|
||||||
0 |
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 xk |
|
|
|
|
1 1 |
|
|
|
|
|
|
|
|
2 0 sin xi x dx |
2 x sin x xk dx |
||||||||||
|
w 1 w 0 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
1 cos 1 xk |
1 cos xk |
1 1 cos xk |
1 1 cos 1 xk 1. |
|||||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
Таким образом показано, что функция w sin r 2 действительно является |
||||||||||||||||
фундаментальным решением. Выражение |
|
|
|
|
|
|||||||||||
|
|
1 |
|
|
|
|
|
~ |
|
|
|
|
|
|
1 |
|
|
|
~ |
|
w dx |
|
|
~ |
|
|
|
|
|||||
|
|
u |
w |
|
u |
0 w 0 u 1 w 1 xwdx 0, |
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
полученное в примере 6.1, с учетом уравнения w w x xk принимает форму
1
u~ xk u~ 0 w 0 u~ 1 w 1 xwdx,
0
позволяющую определить значение функции u~ в точке xk. Подстановка фундаментального решения в это уравнение приводит к решению
117
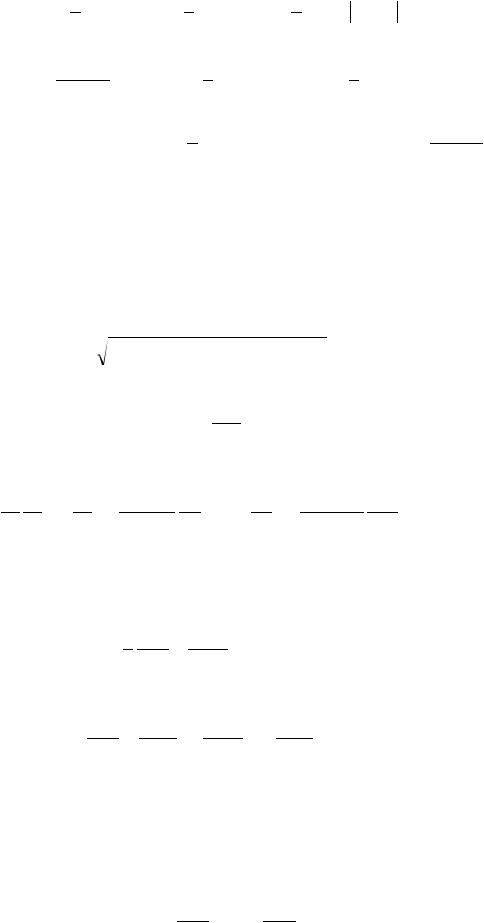
|
~ |
~ |
|
|
1 |
~ |
1 |
|
|
1 |
1 |
|
|
|
|
|
|
|
2sin xk u 1 |
2cos 1 xk |
2 |
xsin x xk |
dx |
|
|||||
|
u xk u 0 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
1 cos1 |
|
|
tg 1 1 |
|
|
1 xk |
|
|
|
1 1 |
|
|
|
|
2cos1 |
sin xk |
|
2 |
cos1 xk |
2 0 |
xsin xk x dx |
2 x xsin x xk dx |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
1 |
xk |
sin 1 xk cos 1 xk |
sin xk |
xk . |
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
cos 1 |
|
Точное решение рассмотренной задачи имеет вид
u x sin x x. cos 1
Пример 6.3. Рассмотрим уравнение (6.1), записанное для трехмерной бесконечной области с изотропными свойствами. Поле k, порождаемое точечным источником, имеющим координаты (xi, yi, zi), в этом случае зависит
лишь от расстояния |
|
r |
x x |
2 y y |
2 |
z z |
2 |
между источником и |
||||
|
|
|
|
i |
i |
|
|
i |
|
|
|
|
произвольной точкой (x, y, z). Решением является функция |
|
|
||||||||||
|
|
|
|
|
k 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
4 r |
|
|
|
|
|
|
|
Для сферической системы координат оператор Лапласа имеет вид |
||||||||||||
1 |
2 |
|
|
1 |
|
|
|
|
|
1 |
2 |
. |
r |
|
|
|
sin |
|
|
|
2 |
||||
r2 r |
|
r |
|
r2 sin |
|
|
r2 sin2 |
|
||||
Поскольку решение задачи не зависит от направления, определяемого углами , , уравнение (6.1) принимает вид (источник находится в начале
системы координат, r = 0) |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
k |
2 |
k |
(r). |
|
|||
|
r |
r |
r2 |
|
||||||
|
|
|
|
|
|
|
|
|||
Дифференцирование решения дает выражения |
|
|||||||||
|
k |
1 |
, |
2 |
k |
|
1 |
, |
||
r |
4 r2 |
|
|
2 r3 |
||||||
|
|
r2 |
|
|
||||||
при подстановке которых дифференциальное уравнение для r 0
удовлетворяется тождественно, поскольку r  r 0 0. Для исследования случая r = 0 рассматривается шар радиуса с центром в начале координат (здесь находится точечный источник). Интегрирование уравнения (6.1) по этому шару с использованием теоремы Гаусса [] приводит к выражению,
r 0 0. Для исследования случая r = 0 рассматривается шар радиуса с центром в начале координат (здесь находится точечный источник). Интегрирование уравнения (6.1) по этому шару с использованием теоремы Гаусса [] приводит к выражению,
kd |
k d |
k d . |
||
|
|
n |
|
r |
118

Подстановка сюда требуемой производной дает
kd |
1 |
2 d |
1 |
2 d 1. |
|
|
|
4 r |
|
4 |
|
При интегрировании учтено, что на поверхности сферы r = = const. Но это как раз и означает выполнение уравнения (6.1) независимо от величины
радиуса сферы, поскольку r d 1. В табл. 1 Приложения представлен ряд
фундаментальных решений из монографии [] для некоторых дифференциальных уравнений.
При получении уравнения (6.2) предполагалось, что точечный источник располагается внутри области . Рассмотрим случай, когда особая точка попадает на границу области, например, xk Q . Рассматривается часть области ГQ с точкой xk (рис. 6.0), причем эта особая точка окружена внешней полусферой с радиусом, равным .
Рис. 6.0. Попадание точечного источника на границу ГQ области
Рассматривается выражение
um |
k |
d um |
k |
d , |
(6.3) |
n |
n |
||||
Q |
|
|
|
|
|
где Q – – поверхность Q без круга, вырезанного полусферой . Производная в подынтегральном выражении равна
k |
k |
|
1 |
n |
r |
|
4 r2 |
и на поверхности сферы постоянна, причем r = . Второе слагаемое в левой части выражения (6.3) равно
um |
|
k |
|
1 |
2 umd |
1 |
|
1 |
|
umd |
|
|
u |
m |
|
|
d |
|
|
|
|
2 |
|
|
|
, |
|||||
n |
4 |
2 |
|
2 |
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||
где um – среднее по поверхности полусферы значение um.
119
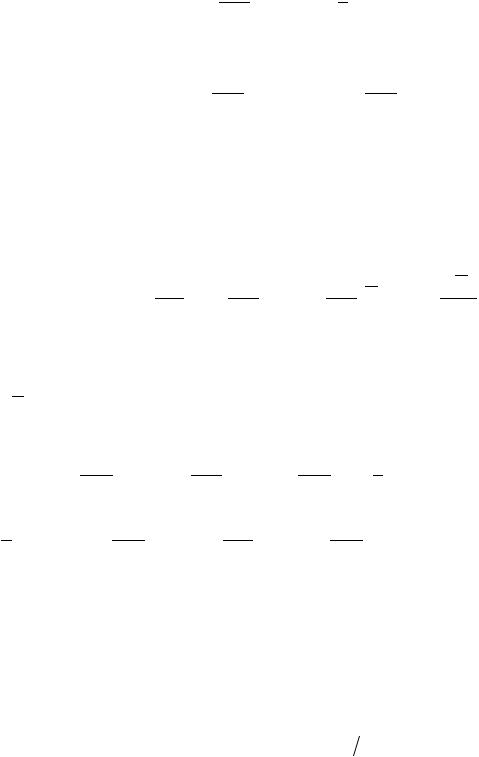
Отсюда следует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
m |
k d 1u |
m |
x |
k |
|
. |
|
|||||||
|
|
|
n |
0 |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Первое слагаемое соотношения (6.3) преобразуется к виду |
|||||||||||||||||
|
u |
m |
k |
d |
|
u |
m |
k |
d |
. |
|||||||
|
|
|
n |
0 |
|
|
|
n |
|
|
|||||||
Q |
|
|
|
|
|
|
Q |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Здесь Q соответствует границе ГQ |
с выколотой точкой xk. Для другого |
||||||||||||||||
интеграла, входящего в соотношение (6.2), выполняются аналогичные преобразования:
Q kd Q kd ,
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
d |
|
Q |
1 |
d |
1 |
|
Qd |
1 |
Q2 2 Q 0 |
, |
|
|||||||||
|
k |
|
|
|
4 r |
|
|
4 |
|
4 |
|
|
|
2 |
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
Q |
d |
|
Q |
d |
, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
k |
|
|
0 |
|
k |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Q |
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
где Q – |
среднее по поверхности полусферы |
значение Q. |
В итоге, |
после |
||||||||||||||||||
преобразований получается выражение |
|
|
|
|
|
|
|
|
|
|||||||||||||
um xk |
U |
k |
|
|
|
k |
um |
|
|
|
k |
|
|
|
1 |
|
Q kd f kd , |
|||||
n |
d |
n |
d um n |
d |
2um xk |
|||||||||||||||||
|
|
U |
|
|
|
|
U |
|
|
|
|
Q |
|
|
|
|
|
Q |
|
|
|
|
1 |
|
|
|
k |
|
|
|
um |
|
|
k |
d Q kd f kd . |
|
|||||||||
2um xk U |
n |
d k |
n d um |
n |
(6.4) |
|||||||||||||||||
|
|
|
U |
|
|
|
U |
|
|
|
|
Q |
|
|
|
|
Q |
|
|
|
|
|
В случае попадания особой точки на границу ГU результат преобразований получается аналогичным. Выражение (6.4) позволяет определять искомое решение на всей границе Г области не прибегая к построению решений уравнения (6.0), используя лишь фундаментальное решение, что значительно сокращает необходимые вычислительные ресурсы.
Для удобства последующих преобразований вводятся обозначения:
~ |
U, |
|
x U , |
~ |
um n, |
x U , |
|
u |
, |
x Q; |
q |
x Q. |
|||
|
um |
|
Q, |
||||
Пусть граница Г области аппроксимируется набором граничных элементов в виде отрезков прямых Гj. Пусть NU элементов принадлежат границе ГU и NQ элементов – границе ГQ, то есть всего N = NU + NQ элементов. В этом случае на границе ГU неизвестны NU величин um n, на границе ГQ подлежат определению NQ значений um. Всего N = NU + NQ неизвестных.
n, на границе ГQ подлежат определению NQ значений um. Всего N = NU + NQ неизвестных.
120
