Boyarshinov_ChM_T3

С помощью различных численных методов построим приближенные решения этого уравнения в виде

um x x 1 x 0 1x 2x2 ,

удовлетворяющем граничным условиям (1.12). Для упрощения будем удерживать только два слагаемых в разложении решения по степеням аргумента x:

Погрешность получаемого приближенного решения будем оценивать с помощью точного решения (1.13).

В соответствии с идеей метода потребуем равенства нулю от взвешенной по всей области интегрирования невязки 1:

1

где k, k = 0, 1, 2, … – полная система взвешивающих функций.

Метод моментов

Выберем последовательность 1, x, x2, … в качестве взвешивающих функций k. В соответствии с (1.16) получим выражения:

Интегрирование приводит к системе двух алгебраических уравнений относительно неизвестных коэффициентов 0 и 1:

методом моментов, по сравнению с точным решением (1.13).

11

Метод коллокаций

В качестве взвешивающих функций k выбираются –функции Дирака. В частности,

где x1 и x2 – произвольные точки отрезка [0, 1]. Подсчитаем выражения (1.16) для этого случая:

Иными словами, в этом методе требуется удовлетворение невязки не в среднем по всей области интегрирования, а в конечном числе точек отрезка,

алгебраических уравнений:

12

Метод подобластей

Пусть рассматриваемая область разделена на m подобластей i, которые могут перекрывать друг друга. Взвешивающие функции, которые в этом случае можно назвать индикаторными, определяются следующим образом:

Для задачи (1.11) – (1.12) в качестве подобластей рассмотрим 0 0,12 и 1 0,1 . Теперь соотношения (1.16) имеют вид:

Интегрирование приводит к системе уравнений

13

Метод наименьших квадратов

Построим функционал

1

1 u1 12dx,

0

минимум которого, равный нулю, достигается при 1 0. Поскольку1 0, 1 , условия экстремума функционала, согласно теореме Лагранжа, можно представить в виде

Последнее выражение можно трактовать как вариант метода взвешенных невязок с весовыми функциями

14

Метод конечных разностей

15

В соответствии с идеей метода конечных разностей строится локальная аппроксимация решения (для трех соседних узлов разностной сетки с номерами i, j и k, соответственно) в виде:

квадратичные функции, принимающие значения 1 в своем (одноименном) узле и 0 в соседних узлах. Невязка дифференциального уравнения (1.11) на таком приближении решения для всего отрезка [xi, xj] длиной h имеет вид:

где x h2 – расстояние между двумя соседними узлами, то есть шаг сетки. Последнее выражение является конечно-разностной аппроксимацией уравнения (1.11), применяемой в сеточных методах.

-функция Дирака

В различных вопросах математического анализа термин функция приходится понимать с различной степенью общности. Иногда рассматриваются непрерывные функции, в других случаях приходится иметь дело с многократно дифференцируемыми функциями. В ряде случае классическое определение функции как правила, ставящего каждому значению x из области определения этой функции соответствующего значения f(x), оказывается недостаточным.

Например, распределение масс вдоль прямой удобно задавать плотностью этого распределения. Однако, если на прямой имеются отдельные точки, несущие сосредоточенную положительную массу, то плотность такого распределения не может быть описана никакой обычной функцией. Применение классического аппарата математического анализа для решения целого ряда задач приводит к невозможности выполнения некоторых операций, когда функцию, не имеющую производную, невозможно продифференцировать, если эту производную понимать в обычном смысле. Оказывается, что подобные

16

затруднения можно преодолеть введением понятия обобщенной функции. В физике интуитивное понятие обобщенной -функции введено и используется достаточно давно, значительно раньше, чем была построена строгая математическая теория обобщенных функций.

Расширение понятия функции

Пусть f – фиксированная функция одной переменной, интегрируемая на каждом конечном интервале; – непрерывная функция, обращающаяся в нуль вне некоторого конечного интервала1. Каждой такой функции с помощью фиксированной функции f можно сопоставить число

Иначе говоря, f можно рассматривать как линейный функционал на некотором пространстве финитных функций. Однако функционалами вида (1.17) не исчерпываются все функционалы, которые можно ввести на таком пространстве. Сопоставляя каждой функции ее значение в точке x = 0, можно получить функционал, не представимый в виде (1.17). Таким образом, функции f естественным образом включаются в некоторое более широкое множество – совокупность всех линейных функционалов на финитных функциях.

Пространство основных функций

Пусть K – совокупность всех финитных функций , имеющих непрерывные производные всех порядков. Вводится понятие сходимости: последовательностьn элементов из K называется сходящейся к K, если существует

интервал, вне которого все n 0, и последовательность производных nk

порядка k (k = 0, 1, 2, …) сходится2 на этом интервале равномерно к k .

Линейное пространство с такой сходимостью называется основным, а его элементы – основными функциями.

Обобщенные функции

Обобщенной функцией, заданной на прямой x , называется всякий непрерывный функционал T( ) на основном пространстве K. При этом непрерывность функционала понимается в том смысле, что T n T , если последовательность n сходится к в основном пространстве K.

Всякая интегрируемая на любом конечном интервале функция f порождает некоторую обобщенную функцию. Выражение

1Такие функции называются финитными.

2Равномерность сходимости по различным k не предполагается.

17

есть непрерывный линейный функционал на K. Такие обобщенные функции называются регулярными, а все прочие, не представимые в виде (1.18), – сингулярными. В качестве примера служит -функция, определяемая в виде

T0 ,

иставящая в соответствие функции ее значение в точке x = 0. Это непрерывный линейный функционал на K, то есть обобщенная функция. Этот функционал обычно записывается в виде

T x x dx,

причем под (x) понимается функция, равная нулю при всех x 0 и обращающаяся в точке x = 0 в бесконечность, так что

x dx 1.

Очевидно, если 1, то

, x 1dx ,1 1 0 1.

Важно подчеркнуть, что -функция Дирака1 есть обобщенная функция, определенная на K.

Еще один пример – смещенная -функция. Пусть

T a .

Как и в предыдущем случае, этот функционал можно представить в виде

T x a x dx.

Дифференцирование обобщенных функций

Пусть T – функционал на K, определяемый непрерывной функцией f,

1 Дирак Поль Адриен Морис [8.8.1902 – 20.9.1984] – английский физик-теоретик, один из основателей квантовой механики. В 1932 году избран членом Лондонского королевского общества, в 1931 – иностранным членом АН СССР и ряда других зарубежных академий и научных обществ. В 1932 году стал профессором Кембриджского университета. В 1933 году ему присуждена Нобелевской премии. Основные труды в математике по функциональному анализу и математической физике (уравнение Дирака, функция Дирака, статистика ФермиДирака).

18

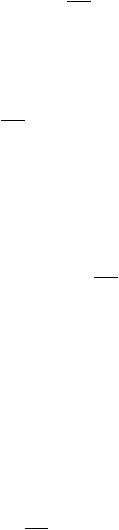
T f x x dx.

Его производной dT/dx называется функционал, определяемый выражением

dT f x x dx.

dx

Интегрирование по частям с учетом того, что каждая основная функция обращается в нуль вне некоторого конечного интервала, дает выражение

Таким образом, получено выражение для производной функционала dT/dx, в котором производная функции f не используется. Отсюда следует, что производной dT/dx обобщенной функции T является функционал, определяемый выражением

dT T . dx

Поскольку имеет непрерывные производные любых порядков, то функционал, определяемый этим соотношением, линеен и непрерывен. То есть является обобщенной функцией. Аналогично определяются вторая, третья и прочие производные. Из определения следует, что всякая обобщенная функция имеет производные всех порядков.

Пример 1.1. Пусть f – регулярная (обычная) функция, производная которой существует и непрерывна. Тогда производная от нее как от обобщенной функции совпадает с ее производной в обычном смысле. Действительно,

dT T f , f , . dx

Пример 1.2. Пусть

Эта функция Хевисайда определяет линейный функционал

h, x dx.

0

В соответствии с введенным определением производной обобщенной функции

19

h , h, x dx x 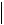0 0 0 ,

0

поскольку обращается в нуль на бесконечности. Таким образом, производная функции Хевисайда1 есть -функция.

Пример 1.3. Из примеров 1.1 и 1.2 ясно, что если f – функция, имеющая в точках x1, x2, … скачки, равные h1, h2, …, и дифференцируема в обычном смысле в остальных точках, то производная от нее как от обобщенной функции представляет собой сумму обычной производной f (в тех точках, где она

существует) и выражения вида hi x xi .

i

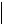Пример 1.4. Определим производную x как обобщенную функцию.

x 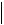0 x dx x 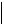0 x dx x dx x dx

h x h x x dx h x h x , .

Таким образом, производная x как обобщенной функции равна h x h x , где h(x) – функция Хевисайда.

Сходимость метода взвешенных невязок

Основные понятия и определения

Основные понятия и определения вводятся в соответствии с [18].

неравенство xn p xn .

1 Хевисайд Оливер [18.5.1850 – 3.2.1925] – английский физик и инженер. В 1891 году избран членом Лондонского королевского общества. Разработал метод символического (операционного) исчисления для решения сложных математических задач механики, электротехники, автоматики. Одновременно с Дж. Гиббсом объединил векторные представления У. Гамильтона и Г. Грассмана в векторное исчисление в его современном виде. Ввел термин орт и название набла для оператора Гамильтона , предложил обозначать векторы жирными символами.

20