
Boyarshinov_ChM_T3
.pdf
f(x) |
|
|
|
|
0,75 |
|
|
|
|
0,5 |
|
|
|
|
0,25 |
|
|
|
|
0 |
|
|
|
|
0 |
0,25 |
0,5 |
0,75 |
x |
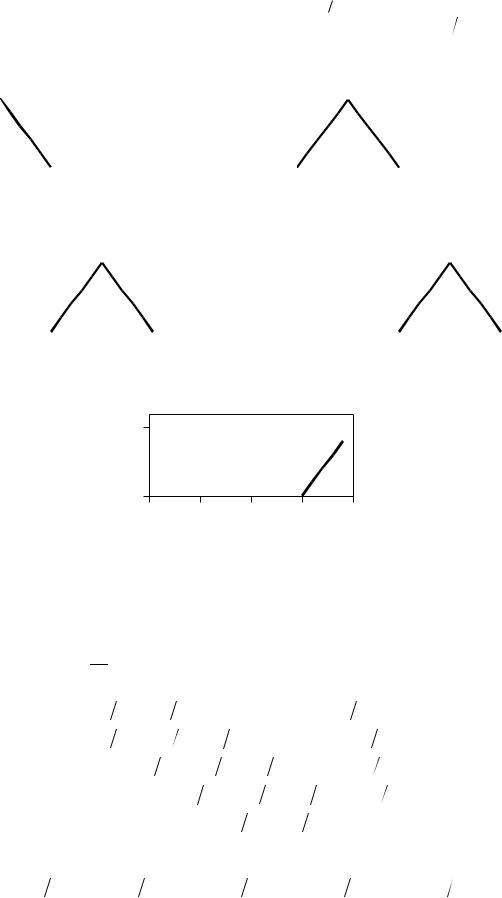
Рис. 2.1. Аппроксимация зависимости f x x2 кусочно-постоянными |
||||
|
пробными функциями |
|
|
|
Кусочно-линейные функции
Набор кусочно-линейных функций представлен на рис. 2.2. Если все узлы отрезка [0, 1] перенумеровать, каждая функция i , i 1,5 будет ассоциироваться с i-м узлом, соответствующим ее номеру. В своем узле значение i равно 1, а в соседних эта функция обращается в 0, изменяясь линейно вдоль прилежащих к этому узлу интервалов. Во всей остальной области пробная функция i тождественно равна 0.
Как и в предыдущем случае, представим заданную функцию в виде разложения (2.0) при m = 5, где
|
1 4x, |
x 0,1 4 , |
|
|
|
|
4x 2, |
x 1 2,3 4 , |
||
x |
|
|
4 |
x |
4 4x, |
x 3 4,1 , |
||||
1 |
|
x 1 4,1 ; |
|
|
|
|
x 0,1 2 ; |
|||
|
0, |
|
|
|
|
0, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
4x, |
x 0,1 4 , |
|
|
|
|
4x 3, |
x 3 4,1 , |
||
|
|
|
x 1 4,1 |
2 , |
5 x |
|||||
2 x 2 4x, |
|
x 0, 3 4 . |
||||||||
|
0, |
x 1 2,1 ; |
|
|
|
|
0, |
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
4x 1, |
x 1 4,1 2 , |
|
|
|
|
|
|
||
x |
3 4x, |
x 1 2, 3 4 , |
|
|
|
|
|
|
||
3 |
|
x 0,1 4 3 |
4,1 ; |
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
В соответствии с выражением (2.1) определяются значения интегралов,
1 |
1 4 |
1 |
1 4 |
1 1dx 1 4x 2 dx 112, |
2 1dx 4x 1 4x dx 1 24, |
||
0 |
0 |
0 |
0 |
31
1 |
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
1 4 |
|
|
|
|
|
|
|
|
3 1dx |
4 1dx 5 1dx 0, |
f 1dx x2 1 4x dx 1 768. |
|
|
|||||||||||||||||||
0 |
|
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1(x) |
|
|
|
|
|
|
1 |
|
|
|
|
|
2(x) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||
0 |
0,25 |
0,5 |
0,75 |
0 |
0,25 |
0,5 |
0,75 |
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
3(x) |
|
|
|
|
1 |
|
|
|
|
|
|
4(x) |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
||||
0 |
0,25 |
0,5 |
0,75 |
0 |
0,25 |
0,5 |
0,75 |
||||||||||||||||
1 5(x)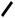
0
0 |
0,25 0,5 0,75 |
x |
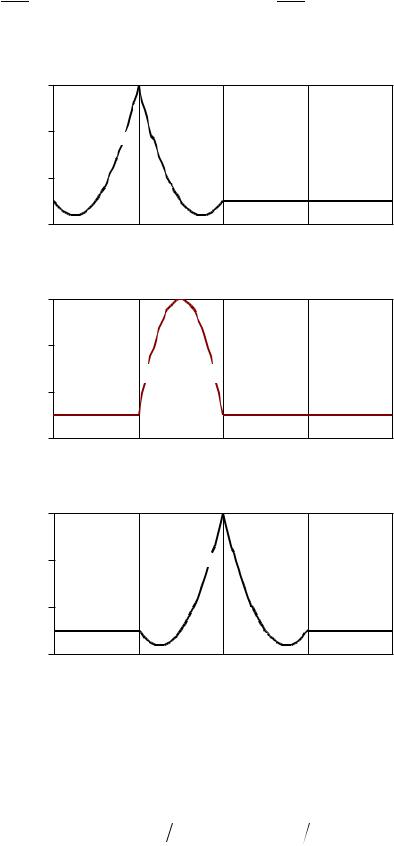
Рис. 2.2. Пробные кусочно-линейные функции
Вычисление остальных интегралов и подстановка полученных значений в выражение (2.1) приводит к системе пяти линейных алгебраических уравнений
относительно ai , i 1,5, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
12 a2 |
24 0a3 0a4 |
0a5 |
1 768, |
|
||||||||||||
a |
|
24 a |
2 |
6 a |
3 |
24 0a |
4 |
0a |
5 |
14 768, |
|
||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
a2 |
|
24 a3 |
|
6 a4 |
24 0a5 50 768, |
(2.4) |
|||||||||
0a1 |
|
|
|||||||||||||||
0a |
0a |
2 |
|
a |
24 a |
4 |
6 a |
24 110 768, |
|||||||||
|
1 |
|
|
|
3 |
|
|
|
|
|
5 |
|
|
|
|
||
|
|
0a2 0a3 |
a4 24 a5 |
12 27 768. |
|
||||||||||||
0a1 |
|
||||||||||||||||
Решением этой системы уравнений являются коэффициенты разложения |
|||||||||||||||||
a1 1 96, a2 |
5 96, |
a3 23 96, |
a4 53 96, a5 |
95 96. |
|||||||||||||
32
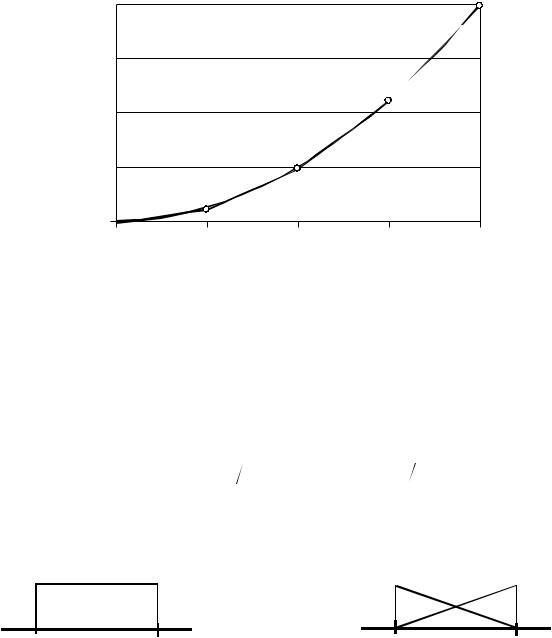
Нетрудно проверить, что найденные коэффициенты можно рассматривать |
||||
в качестве приближенных значений аппроксимируемой функции в узлах |
||||
сеточной области (рис. 2.3). |
|
|
|
|
f(x) |
|
|
|
|
0,75 |
|
|
|
|
0,5 |
|
|
|
|
0,25 |
|
|
|
|
0 |
|
|
|
|
0 |
0,25 |
0,5 |
0,75 |
x |
Рис. 2.3. Аппроксимация зависимости |
f x x2 (сплошная линия) |
|||
кусочно-линейными пробными функциями (–о–) |
|
|||
Из приведенных примеров следует, что при кусочно-постоянных функциях с каждым конечным интервалом [xi, xj] связана одна базисная функция i(x) (рис. 2.4, а), при кусочно-линейной аппроксимации с тем же интервалом ассоциируются две функции (рис. 2.4, б),
i x xj x h |
и j x x xi h, |
где h = xj – xi – длина соответствующего интервала.
(x) |
i(x) |
j(x) |
xi |
xj |
xi |
xj |
|
а |
|
б |
Рис. 2.4. Кусочно-постоянные (а) и кусочно-линейные (б) базисные функции, ассоциируемые с конечным отрезком [xi, xj]
Для второго примера ясен геометрический смысл коэффициентов разложения (2.0) в ряд по базисным функциям
f xi fm xi ai i xi aj j xi ai ,
33
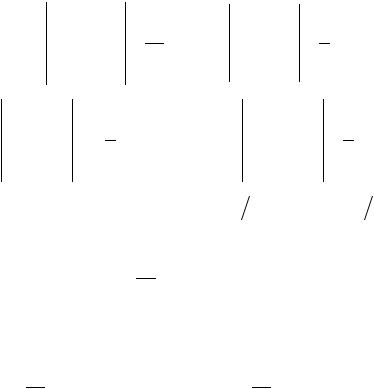
то есть коэффициент ai аппроксимирует значение заданной функции в узле xi разностной сетки. Этот факт широко используется в различных реализациях метода конечных элементов. Рассмотренный способ аппроксимации функций может быть продолжен для получения базисных функций более высоких порядков.
Функции высших степеней
Для построения квадратичной аппроксимации на отрезке [xi, xj] вводится дополнительный узел xk (рис. 2.6), который, как правило, располагается в его центре. Первая функция конструируется в виде
i x x2 x .
Потребуем, чтобы она удовлетворяла на выбранном отрезке следующим условиям:
i xi 1, i xj 0, i xk 0,
то есть в своем узле обращалась в 1, а в соседних была бы равна 0. Это требование приводит к системе трех линейных алгебраических уравнений
|
|
|
|
2 |
xi |
1, |
|
|
|
|
||
|
|
|
|
xi |
|
|
|
|
||||
|
|
|
x2j |
xj |
0, |
|
|
|
||||
|
|
|
|
2 |
xk |
0 |
|
|
|
|
||
|
|
|
|
xk |
|
|
|
|
||||
относительно коэффициентов , и . Определители этой системы |
||||||||||||
|
x |
2 |
x |
1 |
|
|
|
1 |
|
x |
1 |
|
|
|
i |
i |
1 h3 , |
|
|
|
|
i |
1 h , |
||
x2j |
xj |
0 xj |
||||||||||
|
xk2 |
xk |
1 |
3 |
|
|
0 |
|
xk |
1 |
2 |
|
|
|
|
|
|
|
|||||||
x2 |
1 |
1 |
|
|
|
|
|
|
x2 |
x |
1 |
|
i |
|
1 h |
xk xj , |
|
|
|
i |
|
i |
0 h xk xj |
||
x2j |
0 |
|
x2j |
xj |
||||||||
xk2 0 1 |
2 |
|
|
|
|
|
xk2 |
xk |
2 |
|||
|
|
|
|
|
|
0 |
||||||
позволяют вычислить 2 |
h2 , |
2 xk |
xj |
h2 , |
2xk xj h2 и построить |
|||||||
первую пробную функцию |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x 2 x x |
k |
x x |
|
|
|
||||
|
|
|
i |
h2 |
|
|
|
j . |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
Эта функция удовлетворяет всем предъявляемым требованиям. Аналогичным конструируются пробные функции
|
j |
x |
2 x x |
k |
x x |
|
, |
|
k |
x |
4 x x x x |
j |
|
. |
|
|
|
h2 |
i |
|
|
|
h2 |
i |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
34

Вид этих квадратичных функций, ассоциированных с отрезком [xi, xj], представлен на рис. 2.6. На рис. 2.6 показаны те же функции, ассоциированные с узлами отрезка.
1 |
i(x) |
k (x) |
j(x) |
0,6 |
|
|
|
|
|
|
|
0,2 |
|
|
|
-0,2 |
xi |
xk |
xj |
|
|||
Рис. 2.5. Квадратичные пробные функции на отрезке [xi, xj] |
|||
В общем случае для построения на отрезке [xi, xj] системы базисных функций степени p
r x r xp r xp 1 r , |
r 1, p 1 |
следует ввести дополнительно (p – 1) узлов. Коэффициенты , , ..., могут быть определены из решения соответствующих систем линейных алгебраических уравнений
1xip 1xip 1 1,
1xjp 1xjp 1 0.
Вместе с тем целесообразно использовать для определения базисных функций способ, используемый при построении полинома Лагранжа,
|
|
k x x |
x xi x xk 1 x xk 1 x xj |
|
. |
|
|
|
|
|
||||||||||||||||||||
|
|
k |
x x |
k |
x |
k 1 |
x |
k |
x |
k 1 |
x |
k |
x |
j |
|
|
|
|
|
|||||||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Очевидно, что в этом случае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
k q, |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
k xq |
|
|
|
|
k q. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
xi, |
Кубические пробные функции, для построения которых внутри отрезка |
|||||||||||||||||||||||||||||
xj вводятся два дополнительных узла с координатами xk |
2xi xj 3 и |
|||||||||||||||||||||||||||||
xq xi 2xj 3, имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
9 x x |
k |
x x |
q |
x x |
j |
|
, |
|
|
k |
x |
27 x x x x |
q |
x x |
j |
|
, |
|||||||||||
|
i |
2h3 |
|
|
|
|
|
|
|
|
|
|
|
|
2h3 |
|
i |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
35
|
q |
x 27 |
x x |
x x |
k |
x x |
j |
|
, |
|
j |
x |
9 x x x x |
k |
x x |
q |
|
|
|
2h3 |
i |
|
|
|
|
|
2h3 |
i |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и показаны на рис. |
2.7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1
0,6
0,2
-0,2
1
0,6
0,2
-0,2
1
0,6
0,2
-0,2
i(x) 
xi |
xk |
xj |
 k (x)
k (x) 
xi |
xk |
xj |
j(x) 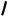
xi |
xk xj |
Рис. 2.6. Квадратичные пробные функции, ассоциируемые с узлами отрезка
Пусть на отрезке [xi, xj] задана естественная координата с началом в
центре отрезка, |
xc xi xj 2. |
2 x xc h, |
Очевидно, что в пределах этого отрезка естественная координата принимает значения 1,1 . В этой системе координат пробные функции представляются следующим образом:
36

– линейные |
|
|
|
|
|
|
|
|
|
|
|
i |
= 1- 2, |
j |
|
= 1 2; |
|
||
– квадратичные |
|
j = 1 2, |
|
|
|||||
i = 1 2, |
|
k = 1 1 2; |
|||||||
– кубические |
|
|
|
|
|
|
|
|
|
= - |
9 ( +1 3)( -1 |
3)( -1) |
|
|
= |
9 ( +1 |
3)( -1 3)( +1) |
||
i |
16 |
|
|
|
, |
j |
|
16 |
, |
k = |
27 ( -1 3)( -1)( +1) |
q |
= - 27 ( +1 |
3)( -1)( +1) |
|||||
|
16 |
|
|
, |
|
|
|
16 |
. |
|
1,2 |
i(x) |
|
k (x) |
|
|
|
|
|
|
0,8 |
|
|
|
|
|
|
j(x) |
|
|
0,4 |
|
|
|
|
|
|
||
|
|
|
q(x) |
|
|
||||
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
-0,4 |
xi |
|
xk |
|
|
|
xq |
xj |
|
|
|
|
|
|
||||
Рис. 2.7. Кубические пробные функции на отрезке [xi, xj] |
|||||||||
Иерархические многочлены
Введенные выше пробные функции обладают существенным недостатком. При необходимости аппроксимации заданной функции с использованием пробных функций более высокого порядка приходится полностью перестраивать систему линейных алгебраических уравнений, получаемую из соотношений (2.1). Это видно из сравнения систем уравнений, получаемых при аппроксимации функции x2 кусочно-постоянными (2.2) и кусочно-линейными (2.4) пробными функциями. Целесообразно так сконструировать систему пробных функций, чтобы при повышении порядка аппроксимации (за счет добавления функций более высокой степени) новая система алгебраических уравнений вида (2.1) формировалась на основе уже имеющейся системы лишь за счет добавления к ней новых столбцов и строк. Построение такой иерархической системы многочленов для произвольного отрезка [xi, xj] начинается с уже известных линейных функций,
0 = 1- 2, |
1 = 1 2. |
Следующая пробная функция строится на основе полинома второй степени,
37

2 = + + 2 .
Потребуем, чтобы в своем узле = 0 (xc) эта функция была равна 1, а в соседних узлах = -1 (xi) и = 1 (xj) – нулю, то есть
2(-1) = - 0,
2(0) = 1,
2(1) = 0.
Решение этой системы уравнений определяет функцию
2 =1- 2 .
Коэффициенты разложения, стоящие при первых трех функциях, будут сохранять свой геометрический смысл, аппроксимируя значения исходной функции в точках xi, xj и xc, соответственно. Для четвертой функции используется кубический полином,
3 = + + 2 + 3,
коэффициенты которого определяются решением системы уравнений
3(-1) = - 0,
3(0) = 0,
3(1) = 0,3(0) = 1.
Отсюда следует, что четвертая функция имеет вид
3 = - 3 .
Аналогично строится пробная функция
4 = 1 2(1- 2), 2
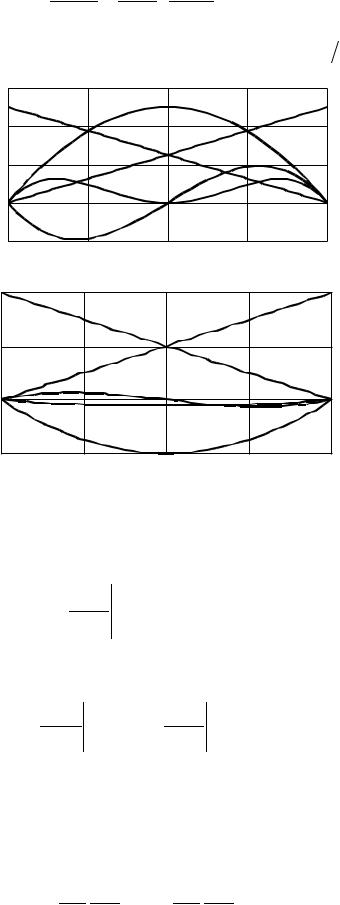
и так далее. Вид пробных функций этой системы показан на рис. 2.8, а. На рис. 2.8, б показан вид пробных функций еще одной иерархической системы,
|
|
=1- ; |
=1+ ; |
для всех k > 2 k |
k 1 k!, |
k четное; |
|
|
|
k нечетное. |
|||||
|
0 |
2 |
1 |
2 |
|
k k!, |
|
Дифференцируя функции этой системы, получаем для четных номеров
d |
k-1 |
|
d |
k-1 |
|
|
k |
|
|
k k 1 2 |
|
||
|
k |
|
|
k 1 |
|
|
|
1 |
|
, |
|||
d |
k 1 |
|
d |
|
|
k! |
|
k k 1 2 |
|||||
|
|
|
|
|
|
|
|||||||
для нечетных
38
|
d |
k-1 |
|
d |
k-1 |
|
|
k |
|
|
|
|
||
|
|
k |
|
|
k 1 |
|
|
|
|
|
. |
|
||
|
d |
k 1 |
|
d |
|
|
|
k! |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
Далее, как для четных, так и для нечетных номеров, dk k |
d k 1. |
|||||||||||||
1,2 |
0(x) |
|
|
|
|
|
|
|
2(x) |
1(x) |
|
|||
|
|
|
|
|
|
|
|
|
||||||
0,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,4 |
|
|
|
|
4(x) |
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
|
|
||||
3(x) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
-0,4 xi |
|
|
|
|
|
|
|
|
|
|
|
xj |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
0(x) |
|
|
|
|
|
|
|
|
|
|
1(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
3(x) |
|
|
|
|
|
|
|||
|
|
4(x) |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2(x) |
|
|||
-0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
xj |
|
|
Рис. 2.8. Примеры иерархических систем пробных функций на отрезке [xi, xj] |
||||||||||||||
Это означает, что |
|
|
|
dk q |
|
1, |
q k, |
d k |
|
0, |
q k, |
|
0 |
|
|
|
|
|
то есть все производные, кроме одной, обращаются в нуль при = 0. Далее, для разложения (2.0) получаем
dq fm |
|
m |
dq k |
aq . |
||
d |
q |
|
ak |
d |
q |
|
|
0 |
k 1 |
|
0 |
||
Следовательно, при q > 2 коэффициент aq аппроксимирует значение производной q-го порядка от исходной функции в точке = 0.
В прикладных задачах математической физики при использовании методов взвешенных невязок часто встречаются интегралы вида
xj |
d i d j |
1 d i d j |
|
x |
dx dx |
dx 1 d d |
d . |
i |
|
|
|
39

В этом случае удобно пользоваться полиномами Лежандра1
0 = 1- 2, |
1 = 1 2, 2 = 2 -1, |
3 = 3 - , |
|||||
|
4 |
=15 4 |
-18 2 |
+3, |
= 7 5 -10 3 |
+3 , …, |
|
|
|
|
|
5 |
|
|
|
для которых |
|
|
|
|
|
|
|
|
|
|
1 d |
d j |
d 0, |
i j. |
|
|
|
|
i |
|
|||
|
|
|
d |
d |
|
||
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
Использование этих полиномов позволяет упростить формирование и решение системы алгебраических уравнений. Вид полиномов Лежандра приведен на рис. 2.9.
1 |
0(x) |
4(x) |
|
|
1(x) |
||
0,5 |
|
||
|
|
|
|
0 |
|
5(x) |
3(x) |
-0,5 |
|
||
|
|
2(x) |
|
-1 |
|
|
|
xi |
|
xj |
|
Рис. 2.9. Система полиномов Лежандра на отрезке [xi, xj] |
|||
Функции двух переменных
Треугольные конечные элементы. Линейная аппроксимация
Пусть вершины простейшего треугольного конечного элемента с вершинами i, j и k на плоскости имеют координаты {xi, yi}, {xj, yj}, {xk, yk} (рис. 2.10). Для такого конечного элемента можно построить три пробные функцииi(x, y), j(x, y) и k(x, y). Рассмотрим процедуру построения кусочно-линейной пробной функции, определенной на этом элементе, в виде
i x, y i i x i y.
Удобно для практических приложений сконструировать эту функцию таким образом, чтобы в своем узле эта функция была равна 1, а в двух других обращалась в 0. Это будет означать, что коэффициенты разложения какой-либо
1 Лежандр Адриен Мари [18.9.1752 – 10.1.1883] – французский математик. Обосновал и развил теория геодезических измерений, первым открыл и применил в вычислениях метод наименьших квадратов. Доказал приводимость эллиптических интегралов к каноническим формам, нашел их разложения в ряды, составил таблицы их значений. В 1783 году стал членом Парижской академии наук.
40
