
Boyarshinov_ChM_T3
.pdf
Уравнения движения в переменных «функция тока – вихрь скорости»
Рассматривается система уравнений Навье-Стокса в безразмерной форме
[], описывающих движение вязкой несжимаемой жидкости, |
|
|
|
|||||||||||||||||||||
vx |
|
vx |
|
vx |
|
P |
|
1 |
|
|
2 |
vx |
|
|
2 |
|
|
|
|
|
||||
vx |
vy |
|
|
|
|
|
|
vx |
, |
(5.3) |
||||||||||||||
t |
x |
y |
x |
|
|
|
x |
2 |
y |
2 |
|
|||||||||||||
|
|
|
|
|
Re |
|
|
|
|
|
|
|||||||||||||
vy |
|
vy |
|
vy |
|
|
P |
|
|
1 |
|
2vy |
|
2vy |
|
|
|
|||||||
|
vx |
|
vy |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
, |
(5.4) |
|
t |
x |
y |
|
y |
|
Re |
|
x |
y |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
v |
|
vy |
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.5) |
|||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь обозначено: x, y – координаты произвольной точки рассматриваемой области, t – время, P – давление, Re LV – число Рейнольдса, L, V – характерные размер области и скорость течения, – вязкость жидкости. Для функции тока уравнение несжимаемости
– число Рейнольдса, L, V – характерные размер области и скорость течения, – вязкость жидкости. Для функции тока уравнение несжимаемости
vx vy 2 2 0x y x y y x
выполняется тождественно. Дифференцирование уравнения (5.3) по переменной y, уравнения (5.4) – по переменной x приводит к выражениям
|
v |
x |
v |
x |
|
v |
x v |
|
2v |
x |
|
|
|
vy |
v |
x v |
|
2v |
x |
|
|
2 P |
|
|
1 |
3v |
x |
|
|
3v |
x |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
, |
|
|
||||||||||||||||||||||
|
t y |
|
|
|
y |
|
x |
|
|
y x |
|
|
y |
y |
|
|
|
|
y |
2 |
y x |
|
|
|
|
|
|
y x |
|
y |
3 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
vy |
|
v |
x |
vy |
v |
|
2vy |
|
|
vy |
vy |
v |
|
2vy |
|
|
2 P |
|
|
|
1 |
3vy |
|
3vy |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
. |
|
|
|||||||||||||
|
t x |
|
|
|
x |
|
x |
|
|
x |
|
|
|
|
x |
y |
|
|
|
x y |
x y |
|
|
|
|
|
|
x |
|
|
|
x y |
2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
Вычитание первого выражения из второго приводит к соотношению |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
vy |
|
|
v |
|
|
|
|
|
vy |
|
v |
x |
|
|
|
|
vy |
|
v |
x |
|
vy |
|
vy |
|
|
v |
|
|
v |
x |
|
vy |
|
v |
x |
|
|
||||||||||||||||||||||
|
|
|
|
|
x v |
x |
|
|
|
|
|
|
|
|
|
v |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
x |
|
|
|
y |
|
|
|
|
|
|
x |
|
|
y |
|
|
|
y |
|
x |
|
|
|
y |
|
|
y |
|
|
x |
|
|
|
|
|
|
|
x |
|
|
x |
|
|
y |
|
|
||||||||||||||
t |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 vy |
|
|
v |
x |
|
|
2 |
vy |
|
v |
x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
x |
|
|
y |
|
|
|
y |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
С использованием уравнения несжимаемости (5.5) и определения (5.2) функции завихренности предыдущее соотношение принимает вид дифференциального уравнения
|
vx |
|
vy |
|
|
1 2 |
|
2 |
(5.6) |
|||
t |
x |
y |
|
x |
2 |
y |
2 . |
|||||
|
|
|
Re |
|
|
|
|
|||||
101
Подстановка формул (5.1) в выражение (5.2) позволяет получить дифференциальное уравнение относительно функции тока ,
vxy vyx x x y y ,
2 |
|
2 |
. |
(5.7) |
|
x2 |
y2 |
||||
|
|
|
Выполненные преобразования позволили тождественно удовлетворить уравнение несжимаемости (5.5) и исключить из уравнений Навье-Стокса давление P. Решение системы уравнений (5.6) и (5.7) позволяет найти распределения функций и , а использование соотношений (5.1) – определить компоненты vx и vy вектора скорости.
С другой стороны, дифференцирование уравнения (5.3) по переменной x, а уравнения (5.4) – по переменной y,
v |
x |
v |
|
v |
x v |
|
2v |
|
|
vy |
v |
|
v |
|
2v |
|
2 P |
|
1 |
3v |
|
|
3v |
|
|
|
||||||||
|
|
x |
|
x |
|
|
x |
|
|
x |
y |
|
x |
|
2 |
|
|
|
|
x |
|
x |
2 |
, |
||||||||||
t x |
|
x |
x |
|
x |
2 |
|
x y |
|
x y |
x |
|
|
|
x |
3 |
|
|
x y |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Re |
|
|
|
|
|
|
|||||||||||||||||
vy |
|
vx |
vy |
|
|
2vy |
|
vy |
vy |
|
|
2vy |
2 P |
|
1 |
3vy |
|
3vy |
|
|||||||||||||||
|
|
|
|
|
|
|
vx |
|
|
|
|
|
|
|
vy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t y |
y x |
y x |
y y |
y |
2 |
|
2 |
|
|
y x |
2 |
|
3 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
Re |
|
y |
|
|
||||||||||||||||||||
и сложение полученных выражений с учетом уравнения несжимаемости (5.5) приводит к соотношению
vy v |
|
v |
2 |
|
vy 2 |
|
2P |
|
2P |
, |
(5.8) |
|||
2 |
x |
x |
|
|
|
|
2 |
|
2 |
|
||||
x y |
x |
|
|
|
x |
|
y |
|
|
|
||||
|
y |
|
|
|
|
|
|
|
||||||
которое можно рассматривать как дифференциальное уравнение относительно давления P в случае, если распределения компонент vx и vy вектора скорости найдены из решения предыдущих уравнений.
Преобразование уравнения несжимаемости (5.5)
|
|
v |
x |
|
vy 2 |
|
v |
x |
2 |
|
|
vy 2 |
|
v |
x |
vy |
, |
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
x |
y |
|
x |
|
y |
|
x y |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
vxx 2 vyy 2 2 vxx vyy
позволяет преобразовать уравнение (5.8) |
к виду |
|
|
|
||||||
2P |
|
2P |
v |
x |
vy |
2 |
vy |
v |
x , |
|
x2 |
y2 |
2 |
|
|
|
|||||
|
x |
y |
|
x y |
||||||
а с учетом формул (5.1) записать это уравнение в форме
102
|
2 |
P |
|
|
2 |
P |
|
2 |
|
|
2 |
|
|
|
2 |
|
|
2 |
||
|
|
|
|
|
2 |
|
|
|
|
|
|
. |
||||||||
x |
2 |
y |
2 |
x |
2 |
y |
2 |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
x y |
|
||||||||||||
Граничные условия
Поскольку в прикладных задачах краевые условия обычно ставятся в естественных переменных vx, vy и P, рассмотрим особенности постановки граничных условий для функций тока и завихренности.
Граничные условия для функции тока |
|
|
|
||
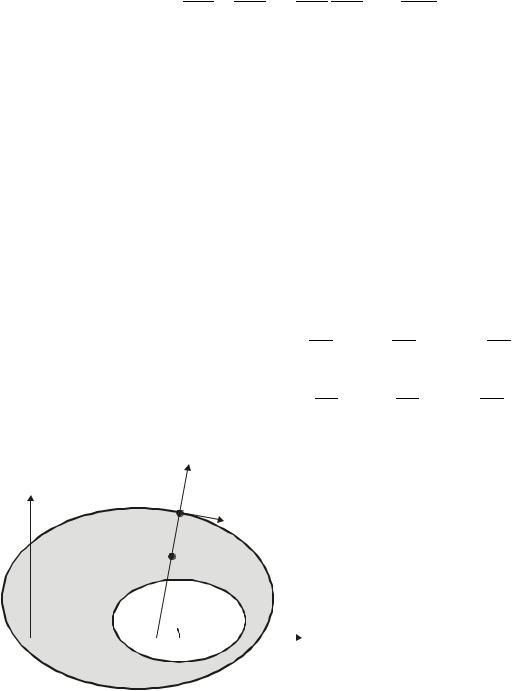
Пусть n cos , sin |
– вектор единичной внешней нормали к границе |
||||
рассматриваемой области |
, |
sin , cos |
– |
единичный |
касательный |
вектор (рис. 5.0). Проекции |
вектора скорости |
на |
n и |
определяются |
|
выражениями |
|
|
|
|
|
|
vn |
vx cos vy |
sin cos |
sin , |
|
|
|
|
y |
x |
|
|
v |
vx sin vy |
cos sin |
cos |
. |
|
|
|
y |
x |
n |
|
|
n |
|
|
|
y |
|
A |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
B |
Рис. 5.0. Схема расчетной области |
||
|
|
|
|
|
|

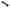


x
Из первого выражения следует, что
vnd .
Поскольку функция определяется с точностью до константы, граничные значения функции тока определяются выражением
s |
|
s vnds, |
(5.9) |
0 |
|
103

где s – дуговая координата, отсчитываемая вдоль границы Г от точки A, для которой принято 0 0.
Граничные условия для функции завихренности
Для записи граничных условий для функции завихренности на твердой границе выбирается произвольная точка A. На расстоянии l от нее по нормали в глубь области выбирается точка B (рис. 5.0). Вблизи точки B функция тока разлагается в ряд Тейлора
l |
|
l2 2 |
O l2 . |
|
B A |
n |
A |
2 n2 |
A |
|
|
|
||
Поскольку, как показано ранее, 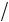 n v ,
n v , 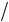 vn , и, согласно (5.7),
vn , и, согласно (5.7),
A |
2 |
|
2 |
2 |
|
2 |
v |
|
2 |
, |
|||||||||||
|
x |
2 |
|
y |
2 |
|
|
|
2 |
|
n |
2 |
|
|
|
n |
n |
2 |
|
||
|
|
|
|
|
A |
|
|
|
|
A |
|
|
|
A |
|||||||
получается
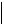 B
B 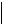 A lv
A lv  A l22 vn A O l2 .
A l22 vn A O l2 .
Отсюда следует формула Тома [] для функции завихренности,
|
2 |
|
|
2v |
|
vn |
. |
(5.10) |
A |
l2 |
A |
B |
l |
A |
|
A |
|
В частности, vn 0 вдоль твердой границы, и формула (5.10) упрощается,
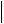 A l22
A l22 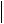 A
A 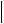 B 2l v
B 2l v 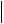 A .
A .
Соотношения метода взвешенных невязок
Решения дифференциальных уравнений (5.6) и (5.7) в пределах отдельного треугольного конечного элемента представляются в форме
m x, y r r x, y ,
r i, j,k
m t,x,y r t r x,y ,
r i, j,k
где, как и ранее, пробные кусочно-линейные функции для p-го конечного элемента имеют вид
r x, y r r x r y, |
r i, j,k, |
r , r t – узловые значения функций m и m, подлежащие определению.
104

Разрешающие соотношения для функции тока
Пусть приближенное решение m уравнения (5.6) для некоторого момента времени t известно. Невязка уравнения (5.7) на приближенном решении m взвешивается по области p конечного элемента с использованием тех же пробных функций q x,y , q i, j,k, Остроградский
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
d 0, |
|
|
|
q i, j,k . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
m |
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
y |
2 |
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Преобразования этого уравнения с использованием теоремы1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Остроградского2-Гаусса приводят к выражению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
m |
q |
|
|
m |
|
q |
|
|
|
|
d |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
q |
|
|
|||||||||||||||||||||||||||
|
|
|
x |
|
x |
|
|
|
|
y |
|
|
y |
|
|
|
q |
|
|
x |
|
|
x |
|
|
|
|
y |
|
|
y |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
m |
|
|
|
|
|
|
|
m |
|
|
d |
|
|
|
m |
q |
|
|
|
m |
|
q |
|
|
|
|
|
|
|
d |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
m |
||||||||||||||||||||||||||||||
|
x |
|
|
x |
|
|
|
|
|
y |
|
|
y |
|
|
|
q |
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
q |
|
|||||||||||||||||||||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
y |
|
|
|
p |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
m d |
|
|
|
m |
q |
|
|
m |
q |
|
|
|
|
|
|
|
|
|
|
d 0, |
|
q i, j,k |
|
|||||||||||||||||||||||||||||||||||
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
m |
|
|
. |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
y |
|
y |
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Учитывая способ представления решений m, |
|
m и соотношение n v |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, полученное выражение можно переписать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
r |
|
|
r |
q |
|
|
r |
q |
|
|
|
|
|
m |
q |
d |
|
|
|
|
q |
d , |
|
q i, j,k |
. |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
v |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
r i, j,k |
|
|
|
|
x |
|
x |
|
|
|
|
y |
y |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С использованием обозначений
1 Теорема Остроградского-Гаусса [2]: поток вектора через замкнутую поверхность Г равен интегралу от дивергенции по объему , ограниченному этой поверхностью,
d d .
2 Остроградский Михаил Васильевич [24.9.1801 – 1.1.1862] – русский математик. С 1816 по 1820 год учился в Харьковском университете, с 1822 по 1828 год слушал лекции О. Коши, П. Лапласа, Ж. Фурье в Париже. В 1828 стал профессором офицерских классов Морского кадетского корпуса, с 1830 – профессором Института корпуса инженеров путей сообщения. В 1830 году избран в Петербургскую академию наук. Занимает должности профессора в Главном педагогическом институте (с 1832 года), Главном инженерном училище (с 1840 года), в Главном артиллерийском училище (с 1841 года). Один из основателей Петербургской математической школы. Основные труды относятся к математическому анализу, теоретической механике, теории чисел, алгебре, теории вероятностей.
105

i |
i i |
i |
||||
|
x |
x |
y |
y |
|
|
|
|
|||||
|
i |
|
j i |
|
|
|
Ap |
x |
y |
j |
|||
p |
x |
|
y |
|
||
|
i |
k |
i |
k |
||
|
||||||
|
x |
x |
|
y |
y |
|
j |
i |
j |
|
i |
|
k |
|
i |
|
k |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
i |
|
|||||||
x |
x |
|
y |
y |
x |
x |
|
y |
y |
||||||||||
|
|
|
|||||||||||||||||
j |
j |
|
j |
j |
|
|
|
j |
|
|
|
j |
|
||||||
x |
x |
|
y |
y |
|
k |
x |
|
|
k |
y |
d , |
|||||||
|
|
x |
|
|
|
y |
|
||||||||||||
j |
|
k |
j |
|
k |
|
k |
|
k |
|
k |
|
k |
|
|||||
x |
|
y |
|
|
|
|
|
|
|||||||||||
x |
|
|
y |
x |
|
x |
|
|
y |
y |
|
||||||||
|
|
|
|
|
|
|
|
|
t |
||
|
|
|
|
|
i |
|
|
t |
|
i |
|
p |
|
, |
|
|
t , |
||||||
|
|
|
j |
p |
|
j |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
t |
|||
|
|
|
|
|
|
|
k |
|
|||
i iCp i j
p i k
j i
j j
j k
k ik j d
k k
полученный результат удобно представить в матричной форме в виде системы линейных алгебраических уравнений относительно узловых значений
i, j , k ,
Ap p Cp p t Vp . |
(5.11) |
Разрешающие соотношения для функции завихренности
Пусть задача (5.11) решена, то есть решение m уравнения (5.7) найдено, в соответствии с формулами (5.1) вычислены компоненты vx и vy вектора скорости. Невязка уравнения (5.6) на приближенном решении m взвешивается по области p конечного элемента с применением пробных функций q x,y ,
|
|
|
|
|
|
|
|
m |
|
|
m |
|
|
m |
|
1 |
|
|
|
2 |
m |
|
|
|
2 |
m |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
t |
|
vx |
x |
vy |
y |
Re |
|
|
x |
2 |
|
y |
2 |
qd 0, |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
m |
d |
|
|
|
|
|
m v |
|
|
|
|
|
d |
1 |
|
|
|
|
2 |
m |
|
2 |
m |
|
|
|
d 0, |
q i, j,k |
|
|||||||||||||||||||
|
v |
x |
|
y |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||||||||
t |
q |
|
|
|
|
x |
|
|
y |
|
q |
|
|
Re |
|
|
|
|
x |
2 |
|
|
|
|
y |
2 |
q |
|
|
|
|
|
||||||||||||||||||
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Слагаемые, входящие в это выражение, преобразуются с учетом |
||||||||||||||||||||||||||||||||||||||||||||||||
представления приближенного решения m, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m qd |
d r t r qd , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
t |
|
|
|
|
|
r i, j,k |
|
|
dt |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
m |
v |
|
m |
|
|
d |
|
|
|
t |
|
|
|
|
|
|
r v |
|
|
|
|
|
d |
|
|
||||||||||||||||
|
|
|
|
|
v |
x |
|
|
y |
|
|
|
v |
x |
|
|
y |
|
|
r |
, |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
y |
|
q |
|
|
|
|
r |
|
|
|
|
|
|
x |
|
|
|
y |
q |
|
|
|||||||||||||||||||
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
r i, j,k |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
106

p 2x2m 2y2m qd p x xm q y ym q xm xq ym yq dp x xm q y ym q d p xm xq ym yq d
|
|
|
|
|
|
m |
qd r |
t |
|
|
r |
|
|
q |
|
|
|
|
r |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
||||||||||||||||||
|
|
|
n |
|
|
x |
|
x |
|
|
y |
|
y |
d . |
|
|||||||||||||||||||||||
|
|
|
p |
|
|
|
|
r i, j,k |
|
p |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Подстановка всех полученных слагаемых приводит к выражению |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
d |
t |
|
|
|
d |
|
|
t |
|
|
|
|
r |
|
|
|
v |
|
|
r |
|
|
|||||||||||||
|
|
r |
|
|
v |
x |
|
|
q |
y |
|
|
|
d |
|
|||||||||||||||||||||||
|
|
dt |
|
|
r |
q |
|
|
r |
|
|
|
|
|
x |
|
|
|
|
|
y |
q |
|
|||||||||||||||
|
r i, j,k |
|
p |
|
|
|
|
r i, j,k |
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
t |
|
|
|
r |
|
q |
r |
|
|
|
|
|
|
|
|
|
|
|
m |
|
d , |
q i, j,k |
|
|||||||||||
|
|
|
|
|
|
q d 1 |
|
|
q |
. |
||||||||||||||||||||||||||||
|
|
r |
|
|
|
x |
x |
y |
y |
|
|
|
Re |
|
n |
|
|
|
|
|
|
|||||||||||||||||
|
Re r i, j,k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
||
Вводя дополнительные обозначения
vx
Qp vxp
vx
i vyx
i vyx
i vyx
yi iyi j
i ky
|
|
j |
v |
|
j |
|
|
|
|
k v |
|
|
|
|
|
|
||
v |
x |
|
y |
|
|
i |
v |
x |
|
y |
|
|
k |
i |
|
|||
|
x |
|
y |
|
|
x |
y |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
j |
v |
|
j |
|
|
|
|
k v |
|
|
|
|
|
|
d , |
|
v |
x |
|
y |
|
|
j |
v |
x |
|
y |
|
k |
j |
|||||
|
x |
|
y |
|
|
x |
y |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
j |
v |
|
j |
|
|
|
|
k v |
|
|
|
|
|
|
|
|
v |
x |
|
y |
|
|
k |
v |
x |
|
y |
|
k |
k |
|
||||
|
x |
|
y |
|
|
x |
y |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
полученное соотношение можно записать в матричном виде
Cp |
|
d |
p |
|
Qp |
|
1 |
Ap |
|
t Wp . |
dt |
t |
Re |
p |
|||||||
|
|
|
|
|
|
|
|
|
Использование разностной схемы Крэнка-Николсона
Cp |
ˆ p p Qp |
1 Ap |
ˆ p p Wp , |
||
|
|
|
Re |
|
2 |
приводит к системе алгебраических уравнений относительно узловых значений
ˆi , ˆ j , ˆ k ,
|
2 C |
|
|
|
|
|
|
|
A |
|
|
ˆ |
|
|
|
|
2 C |
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
2 |
|
|
|
|
|
Q |
|
|
Re |
|
|
|
|
|
|
Q |
|
|
Re |
|
|
|
|
W |
|
||||||||||||||
|
|
p |
|
|
p |
|
|
|
p |
|
|
p |
|
|
|
|
p |
|
|
p |
|
|
|
p |
|
|
p |
|
|
|
|
p |
. (5.12) |
||
Разрешающие соотношения для поля давления
Пусть задачи (5.11) и (5.12) решены и функции m и m определены, компоненты vx и vy вектора скорости найдены в соответствии с выражениями
107
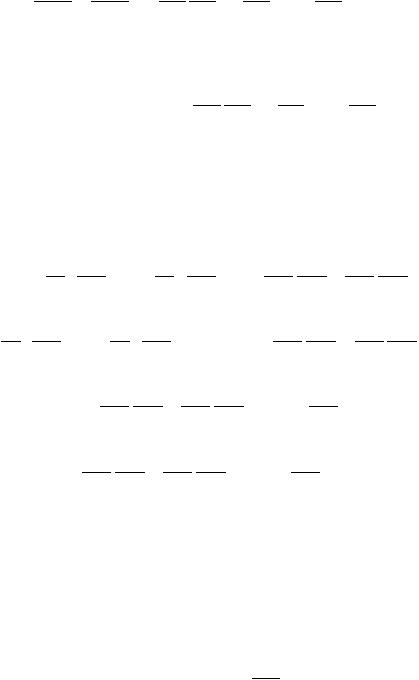
(5.1). Невязка уравнения (5.8) взвешивается по области p конечного элемента с применением пробных функций q x, y ,
|
2 P |
2 P |
vy v |
|
v |
2 |
|
vy 2 |
d 0, |
q i, j,k. |
|||
p |
|
m |
m 2 |
|
x |
x |
|
y |
|
|
|||
|
x2 |
y2 |
x y |
x |
|
|
q |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Использование обозначений
f2 vxy vyx vxx 2 vyy 2,
ипредставления приближенного решения Pm в виде
Pm x,y Pr r x,y ,
позволяет получить систему уравнений для нахождения давления Pm в виде
|
|
P |
|
|
|
|
|
|
P |
|
|
|
P |
q |
|
|
P |
q |
f |
|
|
d 0, |
|
||||||||||||||||
|
|
|
|
m |
|
q |
|
|
|
m |
|
m |
|
|
|
m |
|
|
|
q |
|
||||||||||||||||||
|
x |
|
x |
|
|
|
|
|
|
|
|
y |
|
q |
|
x |
x |
|
|
y |
y |
|
|
|
|
|
|
|
|||||||||||
|
p |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
P |
|
|
|
|
|
|
P |
|
|
d |
|
P |
|
q |
|
P |
q |
|
|
|
|
f |
d 0, |
|||||||||||||||
|
|
|
m |
q |
|
|
|
|
|
|
m |
|
m |
|
|
|
m |
|
|
d |
|
||||||||||||||||||
x |
x |
|
|
|
|
|
|
|
|
y |
|
q |
|
|
|
|
x |
|
x |
|
|
|
y |
|
|
y |
|
|
|
|
q |
|
|
||||||
p |
|
|
|
|
y |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
P |
|
q |
P |
q |
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
m |
|
|
|
|
|
|
m |
|
qd f qd , |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
x |
x |
|
y |
y |
d |
n |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
p |
|
|
|
|
|
|
p |
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
P |
|
|
r |
q |
|
|
|
q |
|
|
P |
|
|
d |
|
|
f |
d , |
|
|
q i, j,k |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
r |
d |
|
|
m |
q |
|
|
|
. |
|||||||||||||||||||||
|
|
r |
|
x |
x |
|
|
y |
|
|
|
|
n |
|
|
|
|
q |
|
|
|
|
|
|
|
||||||||||||||
|
r i, j,k |
|
|
|
|
y |
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В матричной записи эта система линейных алгебраических уравнений записывается в форме
где
PiPp Pj ,
Pk
Ap Pp f , |
|
|
||
|
P |
i |
|
|
fp |
|
|
|
|
m |
j d |
|||
p |
n |
|
|
p |
|
|
k |
|
|
(5.13)
i
f j d .
k
Алгоритм решения задачи
Вычисления начинаются в предположении, что в начальный момент времени функция завихренности = 0 во всей области . Решением системы уравнений (5.11) определяется распределение функции тока в той же области. По найденному полю с помощью формул (5.1) вычисляются компоненты
108
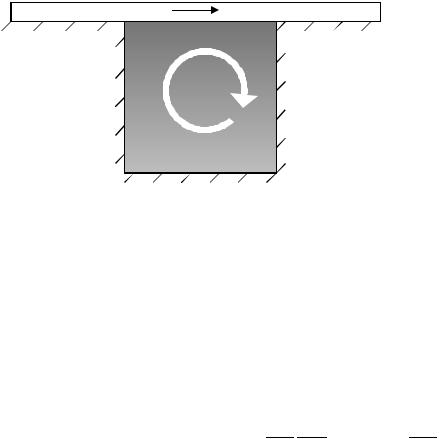
vx и vy вектора скорости. Это позволяет решить систему уравнений (5.12) и определить функцию завихренности ˆ для следующего момента времени. После этого описанная процедура повторяется вновь. Вычисления продолжаются циклически до достижения требуемого момента времени. При необходимости нахождения стационарного решения задачи вычисления продолжаются, пока для двух последовательных моментов времени tn и tn+1 выполняется условие
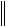 n 1 n
n 1 n  ,
,
где – малое положительное число; используется чебышевская норма, определенная на сеточной области. При найденных полях компонент vx и vy вектора скорости может быть найдено поле давления P с использованием разрешающих соотношений (5.13).
Пример 5.1. Рассматривается течение вязкой жидкости в замкнутой полости (рис. 5.1). Левая, нижняя и правая стенки полости неподвижны, верхняя крышка движется со скоростью V вправо. Требуется исследовать движение жидкости в полости.
V
Рис. 5.1. Схема течения жидкости
в замкнутой полости
Приближенные решения задачи разыскиваются в виде
m x,y i i x, y j j x, y k k x, y ,
m t,x, y i t i x, y j t j x, y k t k x, y ,
где |
r x, y r r x r y, |
r i, j,k |
– линейные в пределах конечного |
|||||
элемента |
пробные функции. |
При |
вычислении элементов матриц |
|||||
Ap , |
Cp , |
Qp встречаются интегралы вида |
|
|
||||
|
|
i jd , |
|
i |
j |
d , |
ux |
i jd . |
|
|
p |
p |
x |
x |
|
p |
x |
109
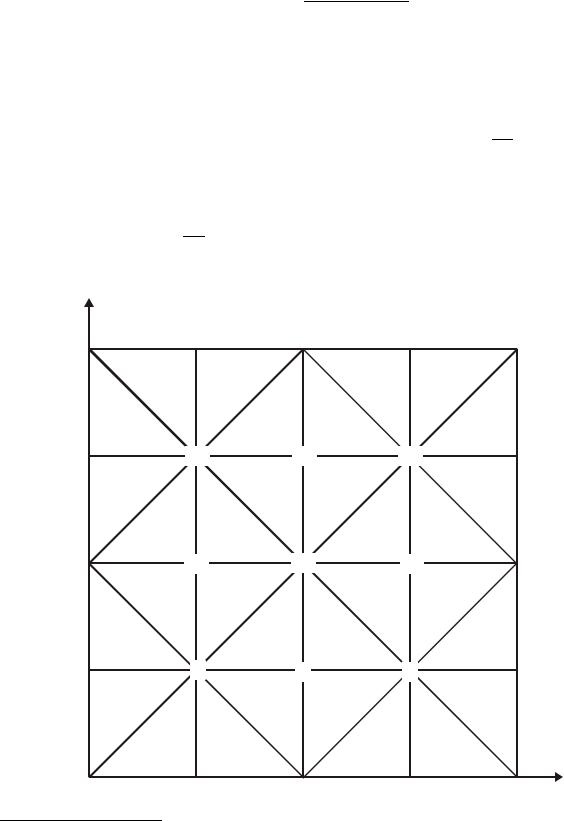
Для их вычисления таких интегралов с линейными пробными функциямиi удобно воспользоваться формулами []
q |
r |
s |
q!r!s! |
2Fp , |
i |
j |
kd |
q r s 2 ! |
|
p |
|
|
|
|
где Fp – площадь p-го конечного элемента. С учетом1 этого выражения получены матрицы
i i |
i i |
j i |
j i |
|||||||||||
|
j |
i j |
j j |
j j |
||||||||||
Ap Fp i |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
i |
k |
j |
k |
j |
k |
|||||||
i |
|
|
|
|
|
|
|
|||||||
k i k i
k j k j ,k k k k
|
2 |
1 |
1 |
|
Cp |
Fp 1 |
2 |
1 |
, |
|
12 |
1 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
Qp
y
|
v |
|
|
|
v |
|
|
|
v |
|
|
|
v |
|
|
|
Fp |
x |
|
i |
|
y |
|
i |
|
x |
|
j |
|
y |
|
j |
|
3 |
vx i |
vy i |
vx j |
vy j |
||||||||||||
|
|
|
i |
vy i |
vx j |
vy j |
||||||||||
|
vx |
|||||||||||||||
vx k vy k
vx k vy k .
vx k vy k
21 |
22 |
23 |
24 |
25 |
26 |
28 |
|
30 |
32 |
25 |
27 |
29 |
|
31 |
16 |
17 |
18 |
19 |
20 |
18 |
20 |
22 |
|
24 |
17 |
19 |
|
21 |
23 |
11 |
12 |
13 |
14 |
15 |
10 |
12 |
|
14 |
16 |
9 |
11 |
13 |
|
15 |
6 |
7 |
8 |
9 |
10 |
2 |
4 |
6 |
|
8 |
1 |
3 |
|
5 |
7 |
|
|
|
|
x |
1 |
2 |
3 |
4 |
5 |
1 Из выражений (5.1) следует, что при аппроксимации функции тока линейными пробными функциями компоненты vx и vy вектора скорости оказываются постоянными в пределах конечного элемента.
110
