Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Глава 3,4

.pdf

Скачиваний:

Добавлен:

11.03.2016

Размер:

546.03 Кб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

Глава 3. ПРЕДЕЛ ФУНКЦИИ

3.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Функция f (x) : X ® ¡ возрастает (убывает) в точке x = x0 X ,

если существует некоторая окрестность этой точки, в которой

ì f

(

)

> f

(

при x > x

;

ì f

(

)

< f

(

при x > x ;ö

(3.1)

0 )

(

)

< f

(

0 )

(

)

> f

(

0 )

í f

при x < x ,

í f

при x< x .÷

Если обозначить

x = x − x0 ,

Df = f (x)

- f (x0 ) , то определение

можно переформулировать следующим

образом:

функция f (x)

возрастает

(убывает)

в точке

x = x0 ,

если

при

Dx ¹ 0

> 0

( Dfx < 0). Точка, в которой функция возрастает (убывает), называет-

ся точкой возрастания (убывания) функции f (x).

	Функция f (x): X → ¡ называется:
– неубывающей на множестве A , если
"x1	, x2 Î A I X x1 ¹ x2	Þ	f (x1 ) - f		(x2 )	³ 0;
			x1	- x2

– невозрастающей на множестве A , если
"x1	, x2 Î A I X x1 ¹ x2	Þ	f (x1 ) - f		(x2 )	£ 0;
			x	- x

– возрастающей на множестве A, если 1					2
"x1	, x2 Î A I X x1 ¹ x2	Þ	f (x1 ) - f		(x2 )	> 0;
			x1	- x2

– убывающей на множестве A, если
"x1	, x2 Î A I X x1 ¹ x2	Þ	f (x1 ) - f		(x2 )		< 0.
			x1	- x2

Неубывающие, невозрастающие, убывающие и возрастающие функции объединяются общим наименованием монотонные функции;

убывающие и возрастающие функции называются также строго мо-

нотонными.

Определение предела функции по Коши

Символическая запись

Определение предела для функции

f (x) , определенной на множестве X

x→x0

(

)

x ® x0

0 < x - x0 < d

lim f

= p

d = d(e) > 0

lim

f (x) = p

x ® x0 +

0 < x - x0

< d

x→x0 +

lim

f (x) = p

f (x) ® p

при

x ® x0 -

ε > 0

(

x Î X

-d < x - x0

< 0

) Þ

f (x) - p

< e

x→x0 −

lim f

(

)

= p

x → ∞

> D

x→∞

lim f

(

)

= p

x → +∞

D = D

(

)

x > D

x→+∞

lim f (x) = p

x → −∞

x < -D

x→−∞

x ® x0

d = d(e) > 0

0 <

x - x0

< d

x ® x0 +

0 < x - x0 < d

f (x) ® p + 0 при

x ® x0 -

ε > 0

(

-d < x - x0

< 0

) Þ 0

< f (x) - p < e

x → ∞

> D

D = D(e) > 0

x → +∞

x >

x → −∞

x < −

x ® x0

d = d(e) > 0

0 <

x - x0

< d

x ® x0 +

0 < x - x0 < d

f (x) ® p - 0 при

x ® x0 -

ε > 0

(

-d < x - x0

< 0

) Þ - e < f (x) - p

< 0

x → ∞

> D

D = D(e) > 0

x → +∞

x > D

x → −∞

x < -D

Символическая запись

Определение предела для функции

f (x) , определенной на множестве X

lim f (x) = ¥

x ® x0

0 <

x - x0

< d

x→x0

d = d(E ) > 0

lim

f (x) = ¥

x ® x0 +

0 < x - x0

< d

x→ x0 +

lim

f (x) = ¥

f (x) ® ¥ при

x ® x0 -

Ε > 0

x ( x X

-d < x - x0

< 0

) Þ

f (x)

x→ x0 −

> E

lim f

(x)

= ¥

x → ∞

> D

x→∞

D = D(E ) > 0

lim f

(

)

= ¥

x → +∞

x > D

x→+∞

lim f (x) = ¥

x → −∞

x < −

x→ −∞

lim f

(

)

= +¥

x ® x0

0 <

x - x0

< d

x→x0

d = d(E ) > 0

lim

f (x) = +¥

x ® x0 +

0 < x - x0

< d

x→x0 +

lim

f (x) = +¥

f (x) ® +¥ при

x ® x0 -

Ε > 0

"x ( x Î X

-d < x - x0

< 0

) Þ f (x) > E

x→x0 −

lim f

(x)

= +¥

x → ∞

> D

x→∞

D = D(E ) > 0

lim f

(

)

= +¥

x → +∞

x > D

x→+∞

lim f (x) = +¥

x → −∞

x < −

x→ −∞

lim f (x) = -¥

x ® x0

0 <

x - x0

< d

x→x0

d = d(E ) > 0

lim f (x) = -¥

x ® x0 +

0 < x - x0

< d

x→x0 +

lim f (x) = -¥

f (x) ® -¥

при

x ® x0 -

Ε > 0

(

-d < x - x0

< 0

) Þ f (x) < -E

x→x0 −

lim f

(x) = -¥

x → ∞

> D

x→∞

D = D(E ) > 0

lim f

(

)

= -¥

x → +∞

x >

x→+∞

lim f (x) = -¥

x → −∞

x < −

x→ −∞

П р и м е р 3.1. Докажем по определению, что lim x2 = 4.

x→2

4Так как понятие предела функции в точке локальное, то, не нарушая общности, можно рассматривать всюду определенную функцию f (x) лишь на интервале X = (1,3). Тогда

ε > 0 δ = ε /5 > 0 "x Î X 0 <

x - 2

< d

x2 - 4

x - 2

x + 2

< 5

x - 2

£ 5

= e .3

Лемма 3.1 (О связи предела функции с односторонними пре-

делами):

Обозначим AÎ¡ U{+¥,-¥},

B Î{+¥,-¥} , C = {+¥,-¥,¥}.

lim

(x) = lim f (x) = A

Û lim f (x) = A .

x→x0

x→x0 −

(x) = A

x→x0

(x) = A.

lim

(x) = lim f

Û lim f

x→+∞

x→−∞

f (x) = B

x→∞

lim

(x) = - lim

Þ lim f (x) = ¥ .

x→x0

x→x0 −

x→x0

lim

(x) = - lim

f (x) = B

Þ lim f (x) = ¥.

x→+∞

x→−∞

f (x)ÎC

x→∞

(x)ÎC .

lim f (x) = ¥

Þ lim

lim

x→x0

(

)

x→x0 +

(

)

ÎC

x→x0 −

(

)

ÎC .

6. lim f

= ¥

lim

lim f

x→∞

x→+∞

x→−∞

Определение предела функции по Гейне

Символическая запись

Определение предела для функции f (x) ,

определенной на множестве X

lim f (x) = S

f (x) ® S

"n xn Î X ,

при x®x

xn¹x0 ,

x→x0

lim xn = x0 и

lim

(

)

= S

f (x) ® S

xn Î X ,

при x®x0

n→∞

xn>x0 ,

x→ x0 +

lim

(

)

= S

f (x) ® S

n xn Î X ,

при x®x0-

<x0 ,

x→ x0 −

"{xn }

(

) Þ lim f (xn ) = S

f (x) ® S

lim f

(

)

= S

xn Î X

n→∞

x→∞

при x→∞

lim

(x) = S

f (x) ® S

lim xn =∞ и

"n xn Î X ,

при x→+∞

xn>0

x→+∞

n→∞

lim

(

)

= S

f (x) ® S

n xn Î X ,

при x→−∞

xn<0

x→−∞

П р и м е ч а н и е : S Î¡ U{¥,+¥,-¥} .

З а м е ч а н и е 1. Чтобы доказать, используя определение предела

функции по Гейне, что предел lim f (x) не существует, достаточно
x→S	при n → ∞ последовательно-
найти две различные, сходящиеся к S

сти аргументов функции {xn′} и {xn′′} такие, что при n → ∞ соответ-

ствующие последовательности значений функции сходятся к раз- ным значениям:

lim f (xn′	) = A, lim f (xn′′) = B , A ¹ B , A, B, S Î¡ U{+¥,-¥,¥} .
n→∞		n→∞
З а м е ч а н и е		2. Чтобы доказать, используя определение предела

функции по Гейне, что предел lim f (x) существует, достаточно по-

x→S

казать, что для двух произвольных, сходящихся к S при n → ∞ , по- следовательностей аргументов функции {xn′} и {xn′′} соответствую-

щие последовательности значений функций сходятся к одному зна-

чению, то есть lim f (xn′	) = lim f (xn′′), где S Î ¡U{+¥,-¥,¥} .
n→∞	n→∞

З а м е ч а н и е 3. Чтобы найти предел lim f (x), используя опреде-

x→S

ление предела функции по Гейне, необходимо сначала доказать,

что он существует, а потом, взяв некоторую последовательность

аргументов {xn } , сходящуюся к S , вычислить предел lim f (xn ) , ко-
x→S	(	x	)	n→∞
торый, при наличии предела lim f		x		, существует и равен ему по

значению.

З а м е ч а н и е 4. Определение предела по Гейне используется в основном в доказательствах теорем и для доказательства несущест- вования предела, в то время как определение предела по Коши

обычно используется для доказательства того, что lim f (x) = A, где

AÎ ¡ U{+¥,-¥,¥} .

x→S

П р и м е р 3.2. Докажем, что предел limsin

не существует.

-1

x→1

{xn¢¢} , для которых

4Выберем две последовательности:

{xn¢}

lim xn′ = lim xn′′ = 1,

но

lim f (xn′ ) ¹ lim f (xn′′).

Например, если

n→∞

xn¢ =1+

и xn¢¢ = 1+

, то

(4n - 3)p

lim f (xn¢ ) = 0, lim f (xn¢¢) = 1.

lim xn′ = 1, lim xn′′ = 1,

n→∞

Значит, limsin

не существует. 3

x -1

x→1

Свойства [конечных] пределов

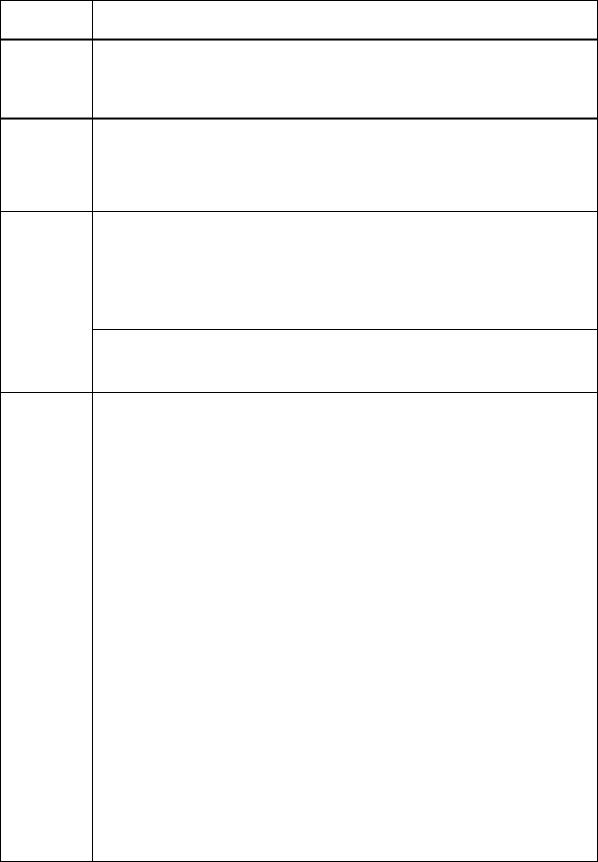
1. Един- ствен-

ность

2. Огра- ничен-

ность

Арифметические	свойства
3.
	4. Свойства пределов, связанные с неравенствами

S = x0	S = x0 +	S = x0 −

Если lim f (x) = p1	и lim f (x) = p2 , то p1 = p2
x→S	x→S

Если f (x) ® p при x ® S , то существует d > 0, такое что f (x) ограничена на множестве

(x0 − δ, x0 + δ)				(x0 , x0 + δ)					(x0 − δ, x0 )
x→S	(	x	)	x→S	(	x	)	= q , то
Если lim f		x		= p и lim g		x		= q , то

lim( f (x) + g (x)) = p + q , lim( f (x) - g (x)) = p - q ,

x→S x→S

lim( f (x) g (x)) = pq

x→S

Если lim f

(

)

= p и lim g

(

)

= q и q ¹ 0, то lim

f (x)

x→S

g (x)

Если f (x) ® p при x → S , и существует δ > 0,

такое что

"x Î(x0 - d, x0 + d) \ {x0}

"x Î(x0 , x0 + d)

"x Î(x0 - d, x0 )

f (x) > q (или f (x) ³ q ), то p ³ q

Если f (x) ® p при x → S , и существует δ > 0,

такое что

"x Î(x0 - d, x0 + d) \ {x0}

"x Î(x0 , x0 + d)

"x Î(x0 - d, x0 )

f (x) < q (или f (x) £ q ), то p ≤ q

Если f (x) ® p и g (x) ® q при x → S и существует

δ > 0, такое что

"x Î(x0 - d, x0 + d) \ {x0 }

"x Î(x0 , x0 + d)

"x Î(x0 - d, x0 )

g (x) ³ f (x), то q ³ p

Пусть f (x) ® p и g (x) ® p при x → S

и существует

δ > 0, такое что

"x Î(x0 - d, x0 + d) \ {x0}

"x Î(x0 , x0 + d)

"x Î(x0 - d, x0 )

g (x) ³ h(x) ³ f (x), то h(x) ® p при x → S

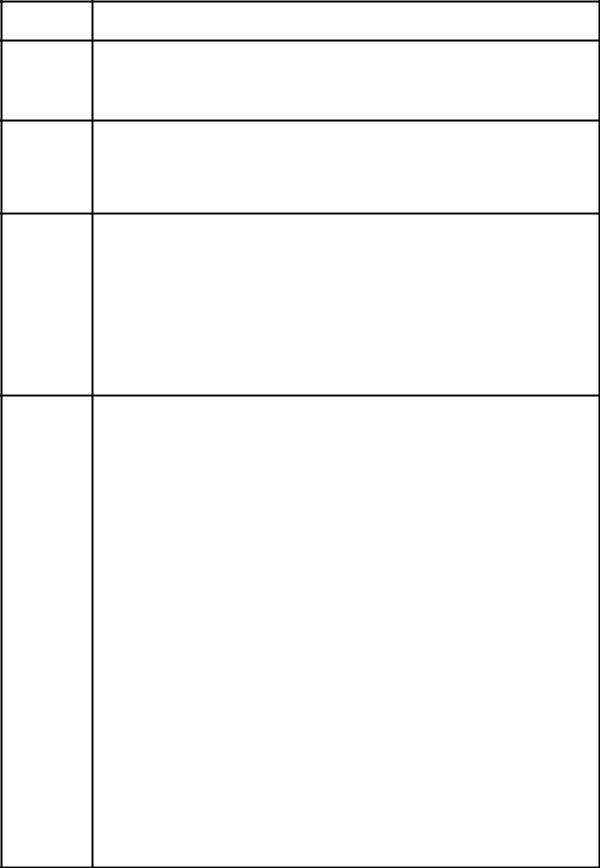
1. Един- ствен-

ность

2. Огра- ничен-

ность

Арифметические	свойства
3.
	4. Свойства пределов, связанные с неравенствами

S = ∞	S = +∞	S = −∞

Если lim f (x) = p1	и lim f (x) = p2 , то p1 = p2
x→S	x→S

Если f (x) ® p при x → S , то существует δ > 0, такое что f (x) ограничена на множестве

(−∞, −δ) U(δ, +∞)

(δ, +∞)

(−∞, −δ)

x→S

(

x→S

(

)

= q

, то

x→S (

(

Если lim f

= p и lim g

)

+ g

(

))

= p

x→S (

(

)

- g

(

))

= p - q

lim

+ q , lim

x→S (

(

)

(

))

= pq

lim

Если lim f

(x) = p и lim g (x) = q и q ¹ 0, то lim

f (x)

g (x)

x→S

→S

Если f (x) ® p при x → S , и существует δ > 0,

такое что

x (−∞,−δ)U(δ, +∞)

x (δ,+∞)

x (−∞,−δ)

f (x) > q

(или f (x) ³ q ), то p ³ q

Если f (x) ® p при x → S , и существует δ > 0,

такое что

x (−∞,−δ)U(δ, +∞)

x (δ,+∞)

x (−∞,−δ)

f (x) < q (или

f (x) £ q ), то p £ q

Если f (x) ® p и g (x) ® q при x → S и существует

δ > 0, такое что

x (−∞,−δ)U(δ, +∞)

x (δ,+∞)

x (−∞,−δ)

g (x) ³ f (x), то q ³ p

Пусть

f (x) ® p и g (x) ® p при x → S и существует

δ > 0, такое что

x (−∞,−δ)U(δ, +∞)

x (δ,+∞)

x (−∞,−δ)

g (x) ³ h(x) ³ f (x), то h(x) ® p при x → S

Функция f (x) : X ® ¡ называется:

– ограниченной сверху на мно-						– неограниченной сверху на мно-
жестве A, если						жестве A, если
$c "x Î A I X f (x) £ c ;						"c $x Î A I X f (x) > c ;
– ограниченной cнизу на мно-						– неограниченной снизу на мно-
жестве A, если						жестве A, если
$c "x Î A I X f (x) ³ c ;						"c $x Î A I X f (x) < c ;
– ограниченной на множестве A,						– неограниченной намножестве A,
$	" Î	A I X	f (x)	£	c ;	если "c $x Î A I X	f (x)	> c .
если c	x

Точные грани функции

Если f (x): X ® ¡ ограниченная функция, то

s = sup f

(

)

1) x A I X f (x) ≤ s ;

′

ε>0 x A I X

f (x )> s −ε

x A

′

< s

′

или s

x A I X

f (x

) > s

i = inf

(

)

1) x A I X i ≤ f (x);

′

ε>0 x A I X

f (x )<i +ε

x A

′

)

′

или i

x A I X

f (x

Если для функции

f (x)

на отрезке [a,b]

точная верхняя грань и

точная нижняя грань достижимы, то

A = sup

(

)

называют мак-

(

)

x [a,b]

)

симальным

значением

, а B

x [a,b]

(

–

минимальным

inf

значением f

(

)

, и пишут A = max f

(

)

B = min f

(

)

x [a,b]

Если f (x) : X → ¡ неограничена сверху (снизу) на множестве A , то

x A

(

)

x A

(

)

= −∞ ).

sup f

= +∞ (inf

Функция

f (x) : X → ¡ является

бесконечно малой (БМ)

бесконечно большой (ББ)

в окрестности предельного значения S , если

x→S

(

)

= 0.

x→S

(

)

= ∞ .

lim f

Свойства бесконечно малых и бесконечно больших функций

БМ функции	ББ функции
1. БМ функция ограничена	1. ББ функция не ограничена.
2. Сумма, разность и произве-	2. Произведение ББ функций есть ББ функ-
дение БМ функций есть БМ	ция. Сумма и разность ББ функций не
функция	обязательно являются ББ функциями

3.Пусть f (x) – БМ функция, а g (x) – ББ функция, тогда:

–функции g (x) + f (x) и g (x) - f (x) являются ББ функциями;

–функция g (x) f (x) может быть любой (то есть и БМ, и ББ, и не яв-

ляться ни ББ, ни БМ)

4. f

(

)

– БМ функция тогда и

x→S

(

)

= ¥ , необходимо

4. Для того чтобы lim f

только

тогда,

когда

функция

и достаточно, чтобы lim

(

)

= +¥ .

f (x)

является БМ

x→S

5. Если

f (x) – БМ функция, и

в некоторой

окрестности пре-

дельного значения

f (x) ¹ 0 ,

5. Если

f (x)

– ББ, то

– БМ функция

f (x)

то функция

является ББ

f (x)

6. Если

f (x)

– ББ функция и в некоторой

окрестности предельного значения S

функция

g (x) удовлетворяет условию

g (x)

> c , то

6. Если

f (x)

– БМ функция, и

произведение g (x) f (x)

– ББ функция

7а. Если lim f

(

)

= +¥

7б. Если lim f

(

)

= -¥

в некоторой окрестности пре-

x→S

дельного

значения

функция

и в некоторой окрестности предельного значе-

g (x)

удовлетворяет

условию

ния S функция g (x) :

g (x)

< c ,

то

произведение

1) удовлетворяет условию

g (x) > c > 0, то

g (x) f (x) – БМ функция

(

)

(

)

(

)

(

)

x→S

= +¥ ;

x→S

= -¥ ;

lim f

2) удовлетворяет условию

(

)

(

)

g (x) < c < 0 , то

(

)

(

)

x→S

= -¥

x→S

= +¥

lim f

Пр и м е ч а н и я :

1.Все свойства остаются справедливыми и для последовательностей, так как

последовательность – это функция натурального аргумента.

2. Все свойства справедливы лишь в некоторой окрестности предельной точки

S , где S Î{x0 , x0 + 0, x0 - 0,¥,+¥,-¥} .

3.2. СУЩЕСТВОВАНИЕ ПРЕДЕЛА ФУНКЦИИ В ТОЧКЕ

Теорема 3.1. Пусть функция		f : X → ¡ возрастает (убывает) на
множестве X	таком, что α = inf X ,		β = sup X .	Причем α X ,
β X . Тогда
ì lim	f (x) = inf f (x),	æ ì lim	f (x) = sup f (x),ö
ïx→α+	x X	ç ïx→α+	x X	÷
í		ç í		÷
ïlim f (x) = sup f (x),		ç ï lim	f (x) = inf f (x). ÷
îx→β−	x X	è îx→β−	x X	ø

4Рассмотрим случай возрастающей функции (случай убываю- щей функции доказывается аналогично).

1. Допустим сначала, что f (x) возрастает и ограничена сверху.

Тогда для множества значений функции существует конечная точ- ная верхняя грань A. Докажем, что это число A и будет искомым пределом при x → β −.

Пусть задано произвольное ε > 0 . Тогда, по определению точной верхней грани, найдется такое значение x′ < β, что f (x′) > A - e .

Ввиду монотонности функции для x > x′ получим f (x) > f (x′) > A - e .

Так как A – верхняя грань множества значений функции f (x) , то можно утверждать, что "x Î X f ( x) £ A < A + e . Таким образом,

для упомянутых значений						x	выполняется неравенство
	f (x) - A	< e. Это и доказывает, что
	f (x) - A	< e. Это и доказывает, что
		lim f	(	x	)	= sup f	(	x	)	.
		x→β−	(		)	x X	(		)

Действительно, в определении предела по Коши при конечном β


достаточно положить δ = β − x′ , а при β = +∞ взять						= x′.
2. Если функция f (x) сверху не ограничена, то,						каково бы ни
было число E ,	найдется такое x′ ,		что f (x′) > E . Тогда для x > x′
получим f (x)	> f (x¢) > E . После		этого	в	определении предела
lim f (x) = +¥	по Коши при	конечном		β	достаточно положить
x→β−		= x′.
δ = β − x′ , а при β = +∞ взять		= x′.
Аналогично доказывается, что lim f (x) = inf f (x). 3
		x→α+			x X

1 / 51 2 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
27.03.2015148.54 Кб6глава 2.docx
#
11.03.2016478.69 Кб20Глава 1.pdf
#
27.03.2015184.32 Кб10Глава 10.doc
#
11.03.2016780.58 Кб9Глава 2.pdf
#
11.03.2016416.27 Кб9Глава 2.pdf
#
11.03.2016546.03 Кб8Глава 3,4.pdf
#
11.03.2016719.99 Кб7Глава 3.2.pdf
#
11.03.2016746.33 Кб8Глава 3.pdf
#
11.03.2016911.85 Кб7Глава 5.pdf
#
11.03.2016660.06 Кб5Глава 6.pdf
#
11.03.2016540.54 Кб7Глава 8.pdf