Глава 3,4
.pdf4Рассмотрим только один случай, когда функция f (x) не убы- вает на [a,b] . Остальные случаи доказываются аналогично.
Так как f (x) монотонна и определена на [a,b] , то она достигает
своих точной верхней и точной нижней граней. |
||
Пусть l2 |
= inf |
f (x), тогда |
|
x [a,b] |
|
|
x>x0 |
|
1) "x > x0 f (x) ³ l2 ; |
||
2) ε > 0 x1 |
> x0 такое, что f (x1 ) < l2 + e . |
|
Так как |
f (x) неубывающая функция, то |
|
|
x x0 < x ≤ x1 Þ l2 £ f (x) < l2 + e , |
|
следовательно, l2 = lim f (x). |
|
x→x0 + |
|
Кроме того, монотонность функции позволяет утверждать, что f (x0 ) |
|
есть нижняя грань для f (x) при x > x0 , следовательно, f (x0 ) £ l2 . |
|
Аналогично доказывается, что l1 = sup |
f (x) = lim f (x) и f (x0 ) ³ l1. |
x [a,b] |
x→x0 − |
x<x0
Следовательно, l1 £ f ( x0 ) £ l2 .3
Следствие. Множество точек разрыва монотонной функции не более чем счетно.
4С каждой точкой разрыва монотонной функции свяжем интер- вал, определяемый значением функции в точке разрыва и одним из
пределов функции при приближении аргумента справа и слева к точке разрыва. Эти интервалы не пересекаются (в силу монотонно- сти функции). Но на прямой может быть не более чем счетное мно- жество непересекающихся интервалов (см. следствие 6 теоремы
Архимеда).3
4.3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ НА МНОЖЕСТВЕ
Функция называется непрерывной на множестве A , если она непрерывна во всех точках этого множества.
З а м е ч а н и е . Если не все точки множества A входят в него с некоторой окрестностью, то это определение меняется. Например,
функция называется непрерывной на отрезке [a,b] , если она непре- рывна во всех точках интервала (a,b) (или, что то же самое, во всех внутренних точках отрезка [a,b] ), а также непрерывна справа в точ- ке a и непрерывна слева в точке b .
107
Функция f (x) называется кусочно-непрерывной на множестве
A, если она непрерывна на множестве A, за исключением, быть может, конечного числа точек, в которых она имеет устранимый разрыв или разрыв 1-го рода.
Теорема 4.5 (теорема Больцано-Коши об обращении функции в нуль). Пусть функция f (x) непрерывна на [a,b] и на концах этого
отрезка принимает значения разных знаков, то есть f (a) f (b) < 0.
Тогда существует точка x0 (a,b) |
такая, что f (x0 ) = 0. |
||||
4Разделим отрезок |
J0 = [a,b] |
пополам точкой x1 = |
a + b |
. Если |
|
|
|||||
f (x1 ) = |
|
|
2 |
|
|
0 , то все доказано. Если нет, то f (x1 ) имеет знак, отличный |
|||||
либо от |
f (a), либо от |
f (b). Обозначим через J1 тот из двух отрез- |
|||
ков [a, x1 ] или [x1,b], на концах которого f (x) принимает значения разных знаков. Поступая так и далее, получим последовательность
стягивающихся (так как длина Jn = b2−n a → 0 при n → ∞ ) отрезков
J0 É J1 É J2 É L. Обозначим через x0 общую точку этих отрезков (она существует в силу леммы о стягивающихся отрезках). Тогда, если Jn = [an ,bn ], то
an ® x0 и bn ® x0 при n → ∞ ,
и, в силу непрерывности f ,
f (an ) → f (x0 ) и
Так как f (an ) f (bn ) < 0, довательно, f (x0 ) = 0.3
f (bn ) → f (x0 ) при n → ∞ .
то lim f (an ) f (bn ) = f 2 (x0 ) ≤ 0 и, сле-
n→∞
З а м е ч а н и е . С помощью этой теоремы устанавливается суще-
ствование корней уравнений. Например, для уравнения 2x = 4x один корень x = 4 очевиден, а существование еще одного корня сле-
дует из того, что f (x) = 2x − 4x при x = 0 принимает значение 1, а
при x = 1/ 2 – значение 
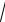2 − 2 < 0.
Кроме того, доказательство теоремы дает простейший алгоритм (алгоритм дихотомии) отыскания корня уравнения f (x) = 0 на от-
резке, на концах которого непрерывная функция имеет значения разного знака.
108
Теорема 4.6 (теорема Больцано-Коши о промежуточном значении непрерывной функции). Пусть функция f (x) непрерывна
на [a,b] , f (a) = a , f (b) = b, и пусть c – любое число, удовлетво- |
||
ряющее условию |
|
|
α ≤ c ≤ β , если α ≤ β ; |
|
β ≤ c ≤ α , если β ≤ α . |
Тогда существует точка x0 Î[a,b] |
|
такая, что f (x0 ) = c . |
|
||
4Рассмотрим функцию g (x) = f ( x) - c . |
||
Если g (a) = 0 или g (b) = 0, то x0 = a или x0 = b .
Если g (a) g (b) ¹ 0, то g (a) и g (b) имеют значения разных зна- ков. По предыдущей теореме существует точка x0 Î[a,b] такая, что g (x0 ) = 0, откуда f (x0 ) = c .3
Теорема 4.7 (критерий непрерывности монотонной функ-
ции). Пусть f (x) определена и монотонна на [a,b] . Тогда для не- прерывности ее на [a,b] необходимо и достаточно, чтобы
– для неубывающей функции
ë |
( |
a |
) |
, f |
( |
|
)û |
0 |
|
[ |
a,b |
] |
f |
( 0 ) |
= l , |
"l Îé f |
|
|
|
b ù |
$x |
Î |
|
|
x |
||||||
– для невозрастающей функции |
|
[ |
|
] |
|
( 0 ) |
|
||||||||
ë |
( |
b |
) |
, f |
( |
a |
)û |
0 |
|
a,b |
f |
= l . |
|||
"l Îé f |
|
|
|
ù |
$x |
Î |
|
|
x |
||||||
4Рассмотрим только случай неубывающей функции. Необходимость. Выполняется в силу теоремы 4.6.
Достаточность. Докажем от противного. Пусть f (x) имеет
разрыв |
в точке |
x0 и не |
убывает |
на |
|
[a,b] . |
Тогда |
для значений |
||||||
l1 = lim |
f (x) и l2 |
= lim f |
(x) выполняются неравенства: |
|
||||||||||
x→x0 + |
|
x→x0 − |
|
|
|
|
|
|
|
|
|
|
|
|
1) l2 |
< l1 (l2 £ l1 в силу монотонности, и l2 |
¹ l1 , так как равенство |
||||||||||||
бы означало равенство пределов |
lim |
f |
( |
x |
) |
и |
lim f |
( |
x |
) |
, а значит, |
|||
|
|
|
x→x0 + |
|
|
|
x→x0 − |
|
|
|||||
непрерывность функции f (x) в точке x0 ); |
|
|
|
|
|
|
|
|||||||
2) l2 £ f (x0 ) £ l1 . |
|
|
|
|
|
|
|
|
|
|
|
|
||
Возьмем l Î(l2 ,l1 ) так, |
чтобы l ¹ f (x0 ) . Тогда |
|
|
|
|
|||||||||
|
|
|
l > f (x) |
при x < x0 ; |
|
|
|
|
|
|||||
|
|
|
l < f (x) |
при x > x0 ; |
|
|
|
|
|
|||||
|
|
|
l ¹ f (x) |
при x = x0 , |
|
|
|
|
|
|||||
|
|
|
109 |
|
|
|
|
|
|
|
|
|
|
|
то есть функция f (x) на сегменте [a,b] не принимает значение l .
Но по условию функция должна пробегать все значения интервала (l2 ,l1 ), так как (l2 ,l1 ) Ì [ f (a), f (b)]. Таким образом, мы пришли к противоречию.3
Лемма 4.1. (о существовании обратной функции). Функция f (x) : X ® Y имеет обратную функцию g ( y) : Y ® X тогда и толь-
ко тогда, когда она строго монотонна. При этом характер монотон- ности функций f (x) и g ( y) совпадает.
Теорема 4.8 (о непрерывности обратной функции). Пусть функция f (x) : X ® Y непрерывна на области определения X и имеет
обратную функцию g ( y) :Y ® X . Тогда g ( y) непрерывна на Y .
Теорема 4.9 (теорема Вейерштрасса об ограниченности не-
прерывной функции). Функция, непрерывная на отрезке [a,b] ,
ограничена на нем. |
|
|
4Докажем от противного. Пусть f (x) не ограничена. Тогда |
||
разделим отрезок J0 |
= [a,b] пополам. В качестве J1 выберем ту по- |
|
ловину, на которой |
f ( x) не ограничена. Снова делим пополам J1 и |
|
выбираем в качестве J2 |
ту половину, на которой f (x) не ограниче- |
|
на. Имеем J0 É J1 É J2 |
É L. Получим последовательность стяги- |
|
вающихся отрезков. Пусть x0 |
– их общая точка. В ней f (x) непре- |
|||||||
рывна, то есть |
|
|
|
|
|
f (x) - f (x0 ) |
|
|
ε > 0 $d = d(e) > 0 "x |
|
x - x0 |
|
< d Þ |
|
|
< e. (4.4) |
|
|
|
|
|
|||||
|
|
|||||||
|
( ) |
|
|
|||||
Пусть e = 1; тогда, согласно (4.4), найдется d 1 -окрестность точ- |
||||||||
ки x0 , в которой f (x) - f (x0 ) <1, и, следовательно, "x Î B(x0 ,1) f (x) = ( f (x)- f (x0 ))+ f (x0 ) £ f (x)- f (x0 ) + f (x0 ) <1+ f (x0 ) .
Значит, f (x) ограничена в d(1)-окрестности точки x0 . Поскольку d(1) > 0, то в ней целиком содержится всякий отрезок Jn , если толь- ко его длина Jn = dn = δ2(1)n < d(1). Но тогда f (x) будет ограничена
и на Jn , что противоречит построению последовательности {Jn}.3
110
Теорема 4.10 (теорема Вейерштрасса о достижении непрерывной функцией точных верхней и нижней граней). Функция,
непрерывная на отрезке, достигает своей точной верхней грани и точной нижней грани, то есть
|
$x1 Î[a,b] |
такое, |
что |
sup |
|
f |
(x) = f (x1 ) , |
|
|
|
||||||||||||||
|
$x2 Î[a,b] |
такое, |
что |
x [a,b] |
|
f |
(x) = f (x2 ). |
|
|
|
||||||||||||||
|
inf |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x [a,b] |
|
|
|
|
|
|
|
|
|||
4Докажем теорему только для |
sup f (x), так как для случая |
|||||||||||||||||||||||
inf f (x) можно рассмотреть функцию f1 (x) = - f ( x). |
|
|
|
|||||||||||||||||||||
Доказательство от противного. |
] |
|
|
|
|
|
( |
|
) |
|
|
|
|
|||||||||||
|
x [a,b] |
( |
x |
) |
и |
"x Î |
[ |
a,b |
A ¹ f |
x |
. Тогда |
|
|
|
||||||||||
Пусть A = sup f |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
"x Î[a,b] A > f (x). |
|
|
|
|
|
||||||||||||||
В силу непрерывности f ( x) , |
функция |
A - f (x) непрерывна и, |
||||||||||||||||||||||
кроме того, "x Î[a,b] |
A - f (x) > 0, следовательно, функция |
|||||||||||||||||||||||
|
|
|
|
|
|
|
g (x) = |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
A - f (x) |
|
|
|
|
|
|
|
|
|||||||||
тоже непрерывна. Тогда по теореме Вейерштрасса g (x) |
ограничена |
|||||||||||||||||||||||
на [a,b] , то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
$B > 0 |
|
|
1 |
|
|
|
< B . |
|
|
|
|
|
|||||||
|
|
|
|
|
A - f (x) |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|||
Отсюда |
A - f (x) > |
|
, |
f (x) < A - |
|
, |
то есть число |
A - |
|
есть |
||||||||||||||
B |
B |
B |
||||||||||||||||||||||
верхняя грань, которая меньше, чем |
A, но это противоречит тому, |
|||||||||||||||||||||||
что A – наименьшая верхняя грань.3
111