Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Глава 5

.pdf

Скачиваний:

Добавлен:

11.03.2016

Размер:

911.85 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

																Глава 5
								Евклидовы и унитарные пространства
								§ 5.1. Определение евклидова пространства
		Говорят, что в действительном																	линейном пространстве L определено
скалярное произведение, если каждой паре векторов																												x, y L поставлено в со-
ответствие действительное число, обозначаемое																									x, y , причем это соответ-
ствие удовлетворяет следующим аксиомам:
0								x, y L;
1	. x, y y, x							x, y L;
2	0	. x, y x, y x, y L, R;
2		. x, y x, y x, y L, R;
0		. x	y, z			x, z y, z						x, y, z L;
3		. x	y, z			x, z y, z						x, y, z L;
4	0	. x, x 0			при x и							x, x 0 при x .
4		. x, x 0			при x и							x, x 0 при x .
		Действительное линейное пространство, в котором определено скалярное
произведение векторов, называется евклидовым пространством.
		Для любых двух векторов														x и y евклидова пространства справедливо не-
равенство КошиБуняковского:
x, y			2	x, x y, y .																												5.1.1
x, y				x, x y, y .																												5.1.1
		Знак равенства в							5.1.1					имеет место тогда и только тогда, когда векторы x
и	y коллинеарны.
		Пример. Докажите, что скалярное произведение в арифметическом про-
странстве R					3	можно ввести по формуле: если																	x 1			, 2 , 3				, y 1, 2 , 3 , то
странстве R						можно ввести по формуле: если																	x 1			, 2 , 3				, y 1, 2 , 3 , то
x, y 10 1 1 3 1 2 3 2 1 2 2 2 2 3 3 2 3 3 .
		Доказательство. Покажем, что аксиомы скалярного произведения выпол-
няются:
1. x, y 10								3		2	3			2		2	2		2		2		3		3		2		3		3
					1		1	1		2				2	1		2		2		2		3		3		2		3		3
				10			1	3	2		3		2		1	2		2				3				2				3
					1		1	1	2				2		1	2		2		2		3		3		2		3		3

2. x,

Пусть

3. x

y, x		x, y R					3	;
y, x		x, y R						;
y 10						3						2	3			2	2				2		2		2	3			3		2
		1			1				1			2				2					2		2		2	3			3		2
	3		3		10						3			2	3			2		2		2	2	2	3			2		3		3
	3		3					1		1			1	2				2	1			2	2	2	3		3	2		3		3
x, y				x, y R					3	, R;
x, y				x, y R						, R;
z 1 , 2 , 3 . Тогда

y, z 10 1 1 1 3 1 1 2 3 2 2 1 2 2 2 22 2 3 3 3 2 3 3 310 1 1 1 2 3 2 1 2 2 2 2 3 3 2 3 3

10 1 1 3 1 2 3 2 1 2 2 2 2 3 3 2 3 3

				x,z y,z																									x, y,z R										3	;
				x,z y,z																									x, y,z R											;
4. x, x				10			2			3												3											2				2																		2
4. x, x				10			1			3							2					3					2					1	2				2					2		3							2			3
							1						1				2										2					1					2					2		3					3		2			3
				10			2		6													2					2				2											2								2		2			3					2	2		2
				10					6													2									2												10									2		10					2		2
						1							1				2										2								2			3				3								1				10		1		2		2	2	3	3
						1							1				2										2								2			3				3								1						1		2		2	2	3	3
												3								2													9
												3										10											9				2		2				2		2										2
				10					1								2					10															2		2				2		2							3			3
									1		10						2																100				2						2						2			3			3
											10																						100
												3								2									11
												3																	11					2		2												2
				10							10																	10								2
									1		10						2											10						2						2		3						3
									1								2																	2						2		3						3
												3								2					11															10
												3													11									2			2			10												2
				10							10														10												2			11
									1		10						2								10									2						11			2			3						3
									1								2																	2									2			3						3
												3								2					11												10						2			11				100
												3													11												10									11				100			2				2
				10					1								2																	2							3												3				3
									1		10						2								10									2			11				3					10				121			3				3
											10														10												11									10				121
											3							2							11												10						2				1		2
		10																																																		0,			причем равенство нулю
		10																																																		0,			причем равенство нулю
								1			10					2									10									2			11				3					11				3
возможно, если												3		0,									2			0, 1 0													, т.е.				x .
		5.1.1. Докажите, что из аксиом скалярного произведения вытекают следу-
ющие свойства:
а) x, y1			y2						x, y1 x, y2																								для любых векторов евклидова пространства;
б ) x, y x, y													для любых векторов x, y																																	евклидова пространства и любого
		действительного числа																												;
		1		2							1												2
в)		x x			, y					x		, y									x			, y ;
г)		, x	0;
г)		, x	0;
	k				e														k				e
д) i xi , j y j															i j xi , y j .
	i 1				j 1													i 1 j 1

5.1.2.Докажите, что в любом действительном линейном пространстве можно определить скалярное произведение.

5.1.3.Введите скалярное произведение в n - мерном арифметическом про-

странстве	R	n	.

5.1.4. Введите скалярное произведение в пространстве нов с действительными коэффициентами степени n .

Mn R многочле-

5.1.5. Пусть

A		ij
A		,

	ij

- квадратные матрицы порядка n над полем

. Покажите, что формула

A, B ij ij

i1 j 1

определяет скалярное произве-

дение в линейном пространстве матриц Rn,n .
5.1.6. Пусть x 1	, 2 и y 1, 2 - произвольные векторы арифмети-
ческого пространства R	2	. Какая из следующих формул определяет скалярное

произведение:

а) x, y 1 1 2 2 ;

б) x, y a 1 1 b 2 2 , a 0, b 0; в) x, y 1 1 2 2 2 2 1;

г)		x, y			2					2					2		2	?
						1		1	1			2	1
			5.1.7. Докажите, что скалярное произведение в																R	2	можно задать формулой

	x, y			a			b			b	2		1	c		2		2
						1 1		1	2
в том и только том случае, если одновременно a 0																			и ac b			2	.

			5.1.8. Пусть a -							фиксированный вектор евклидова пространства L ,														-
фиксированное действительное число. Будет ли множество всех векторов																								x ,
для которых							x, a , линейным подпространством пространства L ?
			5.1.9. Линейное пространство															L разлагается в прямую сумму подпро-
странств						L1, , Lp			. На каждом из подпространств											Li	определено скалярное

произведение. пространстве

Докажите, что можно L , положив: если x и y

ввести скалярное произведение во всем - произвольные векторы из L с разложе-

ниями

по

подпространствам

, , Lp

соответственно

x x1

x p

y y1 y p

, то

x, y x

, y

где скалярное произведение

, y

вычисляется по правилу, заданному в

L .

5.1.10. В арифметическом пространстве

для векторов

и y

вида

,0,0 , y

,0,0

определено скалярное произведение

~ ~

1 1

x , y

а для векторов

вида

x и

0,0, 3 , 4 ,

0,0, 3 , 4

- скалярное произведение

~ ~

3 3 3 4 4 3 2 4 4 .

x , y

Введите (по способу,							описанному в задаче 5.1.9.) скалярное произведение во
всем пространстве R						4	. Вычислите по полученному правилу скалярное произ-

ведение векторов x						1,2,3,4 и y 3,1 3,2 .
			§ 5.2. Длины и углы. Ортогональность. Процесс ортогонализации
					ГрамаШмидта. Ортонормированный базис
		Вещественное или комплексное линейное пространство							L называется
нормированным пространством,								если каждому вектору x L	поставлено в
соответствии вещественное число								x , называемое нормой (или длиной) век-
тора			x , причем выполнены следующие аксиомы:
0			0, если		x ,		0;
1	. x
2	0	. x x			x L, R или C;

30. x y x y x, y L.
		Третья аксиома называется неравенством треугольника ( или неравен-
ством Минковского).
		Всякое евклидово пространство является нормированным, если в нем
норму любого вектора							x определить равенством
									5.2.1
x				x, x
		Углом			между ненулевыми векторами x, y евклидова пространства

называется угол, косинус которого определяется соотношением
cos	x, y		x, y		,	0
	x	y	x, x	y, y


5.2.2

Если среди векторов x, y есть хоть бы один нулевой, то угол между такими векторами считается неопределенным.

Два ненулевых вектора x и y называются ортогональными, если угол между ними равен 2 , т.е. если x, y 0 .

Система векторов называется ортогональной, если в ней все векторы попарно ортогональны.

Во всяком евклидовом пространстве справедлива теорема Пифагора: ес-

ли векторы x и y ортогональны, то	x y	2	x	2		y	2	.

Вектор x называется нормированным, если					x	1.

Система векторов называется нормированной, если нормированы все ее

векторы.
Любой ненулевой вектор			x	можно нормировать, если умножить его на
число	1	.
число		.
	x

Нормированная ортогональная система векторов называется ортонорми-

рованной.

Во всяком n - мерном евклидовом пространстве существует ортонормированный базис.

Любую ортонормированную систему векторов можно дополнить до орто-

нормированного базиса.
От любой линейно независимой системы векторов	x1 , x2 , , xm евклидова
пространства можно перейти к ортогональной системе	y1 , y2 , , ym , состоящей

из ненулевых векторов. Такой переход совершается с помощью процесса ор-

тогонализации ГрамаШмидта по следующим формулам:

y	x	;
1	1

																															x		2	, y
y				x														y		,													2				1		;
y				x														y		,											y			, y					;
		2						2						21					1					21							y			, y
		2						2						21					1					21
																																	1				1
																																								x			, y									x				, y
				x																																						3		1										3			2
y																	y									y			,													3		1			,							3			2		;	5.2.3
y		3															y									y			,											y			, y				,					y				, y			;	5.2.3
								3					31						1				32				2						31							y			, y						32			y				, y
								3					31						1				32				2						31																32
																																										1		1										2			2
. . . . . . . . . . . . . . . . . . . . . . . . . . .
																																																			x		m		, y
y				x															y									y															y				,						m			i		, i 1,2, ,m 1.
y				x															y									y										m,m 1					y	m 1			,				y			, y				, i 1,2, ,m 1.
		m							m						m1					1					m2					2																		mi			y			, y
		m							m						m1					1					m2					2																		mi
																																																					i			i
					Если процесс ортогонализации применять к линейно зависимой системе
векторов, то на некотором шаге обязательно получится нулевой вектор.
					Пусть e1, e2 , , en - ортонормированный базис																																																		n - мерного евклидова про-
странства													L					и для векторов																		x, y L								имеют место разложения
x e																2		e									n		e		,		y e												2	e				n	e .
						1				1						2			2								n			n										1	1				2		2			n		n
В этом случае справедливы равенства:
	x, y													1								2	2									n			n		;
											1			1								2	2									n			n
											2								2									2	;
x, x 1												2									n								;
			i								i									i							i					i 1,2, , n.
							x, e					,											y, e							,		i 1,2, , n.

Пример 1. Применяя процесс ортогонализации ГрамаШмидта и нормирование векторов, постройте ортонормированный базис подпространства, натянутого на заданную систему векторов

x1 11,,0,0 , x2 1,0,1,0 , x3 1,0,0,1 .

Считайте,	что в			R	4	скалярное произведение векторов					x 1 , 2 , 3 , 4 и

y 1, 2 , 3 , 4				задано формулой
x, y	1		2	2				4	4	.	5.2.4
1						3 3
Решение.			Прежде				всего			найдем размерность	линейной оболочки
L x1 , x2 , x3		, которая будет совпадать с рангом системы векторов x1, x2 , x3 :

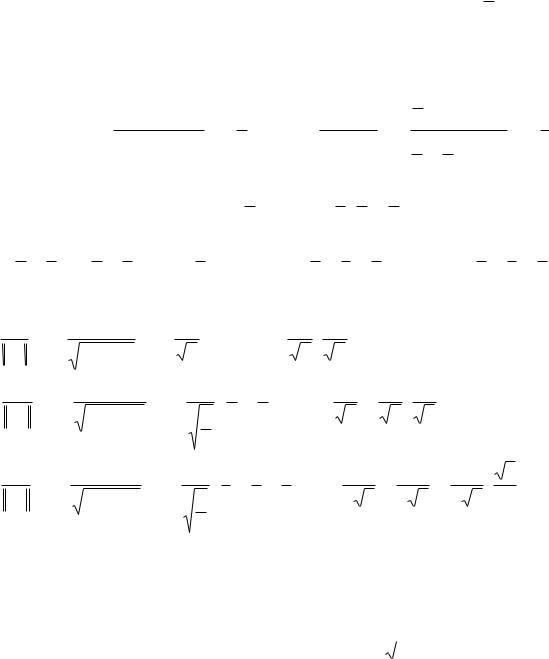
x						1		1			0	0			1		1	0		0		1					1			0			0
			1
																	1									1
	x2						1	0			1	0		~		0	1	1		0 ~				0		1				1			0	,

																	1												1
	x						1	0			0					0		0						0			0
	x		3				1	0			0	1				0		0		1				0			0						1
			3
т.е.				dim L x1					, x2 , x3 3.
По формулам											5.2.3 получим ортогональную систему векторов
	1				1
y			x			1,1,0,0						;
				x2 , y1									1 0 0 0							1	y				x						y		1,0,1,0
		21		x2 , y1																	y		2		x		2			21	y		1,0,1,0
		21				y1, y1							1 1 0 0							2			2				2			21	1
						y1, y1							1 1 0 0							2
					1				1								1		1									1			1
		1					,0			,1 0,0 0								,		,1,0 y2									,			,1,0 ;
		1			2		,0		2	,1 0,0 0								,	2	,1,0 y2								2	,		2	,1,0 ;
					2				2								2		2									2			2

y1 , y2 , y3

21 11,,0,0

							x																																					x																1	0 0 0
								3		, y								1 0									0 0							1													3		, y				2							2	0 0 0													1
										, y								1 0									0 0							1															, y																									1
													1																							,
			31				y			, y															2									2		,			32					y						, y										1			1											3
			31																																				32
																																															2						2												1 0
								1					1																																		2						2							4			4		1 0
																																																												4			4
		3		x		3					31			1					32				2												1											1						1		,			1
y		3				3					31			1					32		y		2
y													y								y						1,0,0,1											1,1,0,0																				,1,0
																																			2												3					2					2
				1		1			1			,0				1				1		,0					0		1		,1 0											1			,			1			,			1					y								1		,		1	,		1
				1								,0										,0					0				,1 0					0									,						,					,1			y				3						,			,			,1 .
						2			6							2				6									3																			3						3									3								3			3
						2			6							2				6									3													3						3						3													3				3			3
Нормируя векторы																				y1			, y2				, y3		, придем к ортонормированной системе векторов:
1					1		1									1							1					1													1				1
1							1																1																				,														;
z						1	y									1				1			y								1,1,0,0												,							,0,0							;
						1										1				1								2														2				2
					y											y	, y											2														2				2
	2					1			2								1									2			1		1			,			1											1				,					1			2
z	2						y		2															y		2																																,								;
z							y									y2 , y2								y															,1,0																			,				,0				;
					y2											y2 , y2														3		2					2													6							6				6
																														2
z					1		y									1							y						1		1		,			1		,		1												1			,				1		,					1		,		3			.
z	3						y	3															y		3								,					,			,1														,						,							,					.
	3							3							y3 , y3										3
					y3										y3 , y3														4 3							3				3						2							3				2			3				2			3			2
																														3

Система векторов

подпространства

z1 ,

x	,
1

z2 , z3

x	2	, x	3

является искомым ортонормированным базисом

Пример 2. Дополните ортонормированную в смысле скалярного произве-

дения 5.2.4 систему векторов x			1		1111,,, , x			1	1,3, 1, 1 до ортонор-
						2

1		6					2	3
		6					2	3
мированного базиса пространства	R	4		.
	R			.

Решение. Поскольку dim R4 4 ,					систему векторов x , x					2	необходимо до-
									1	2
полнить до ортонормированного базиса еще двумя векторами											x3 , x4 . Решение

задачи		проведем
1			2	1,
y	1,1,1,1 , y

3, 1,

два этапа. Сначала систему дополним до ортогонального базиса

y	,
1

векторов y2 , y3 , y4 ,

а затем векторы y3 и y4 пронормируем.
Пусть	y		3	,	3	,	3	,	3	. В силу того, что
		3	1		2		3		4

сываем в матричном виде однородную систему которую получаем:

y1 , y3 0

y2 , y3 0

, запи-

линейных уравнений, решая

	1			1		1					1		1			1	1		1
				3		1						~				4	0		;
1				3		1			1				0			4	0		0
	3			3
3			, 4		- свободные переменные;
4		3		0				3			0;
4		2		0				2			0;
		2						2
	3					3				3			3				3				3		.
	1					2				3			4				3				4		.
	1					2				3			4				3				4
							3	1,				3		0
Выбрав					3			1,				4		0		, фиксируем
Аналогично найдем														y				4	,	4		,
Аналогично найдем														y	4			1	,	2		,
															4			1		2

y		:	y
3			3
4	,		4
3	,		4
3			4

.

1,0,1,0 .

Единственное отличие состоит в

том, что теперь уравнений: y1 , y

решать

4 0 ,

придется

y	2	, y	4	0
	2		4

однородную

и y3 , y4 0

систему не из двух, а из трех

1	1	1	1		1		1	1	1		1		1	1	1		1		1	1
1	3	1		~		0	4	0		~		0	1	2		~		0	1	2
			1						0						1

1
	0	1	0			0	1	2				0	1	0				0	0	2
									1						0

1 1 1

4

4

- свободная переменная;

34 1 44 ;

24 2 34 44 44 44 0;

	4			4				4			4			1	4				4	1	4	.
	1			2				3			4			2	4			4		2	4	.
	1			2				3			4				4			4			4
						4
						4	2							y4	1,0, 1,2 .
Положим					4		2			. Тогда				y4	1,0, 1,2 .
x3		1		y3				1				y3			1	1,0,1,0 ,


			y3						y3 , y3						2
x	4	1		y	4					1		y	4		1		1,0, 1,2 .
	4		y4		4				y4 , y4				4		6
			y4						y4 , y4						6

Построен ортонормированный базис x1 , x2 , x3 , x4 пространства R4 .

Подчеркнем, что данная задача имела не единственное решение. Выбирая зна-

				3	3	4		0), мы по-
чения свободных переменных другими (кроме 3					0, 4	0, 4
лучили бы другие векторы x3 и x4 .
5.2.1. Как изменится угол между ненулевыми векторами x и							y , если
а) умножить вектор			x на положительное число;
б ) умножить вектор			x на отрицательное число;
в) умножить оба вектора на отрицательные числа?
В последующих задачах по аналогии с трехмерным евклидовым простран-
ством упорядоченная тройка векторов x, y и x y произвольного евклидова
пространства рассматривается как треугольник,					о котором говорят, что он
“натянут на векторы			x	и y ”. Точно так же считается, что параллелограмм,
натянутый на векторы x				и y , имеет диагоналями векторы x y и			x y .
5.2.2. В треугольнике, натянутом на векторы					x 2, 1,3, 2		и y 3,1,5,1
пространства R	4	, найдите длины сторон. Определите углы между сторонами

треугольникавекторами				x, y и x y . Какие из этих углов естественно считать

внутренними углами треугольника, какиевнешними? Скалярное произведение

определено формулой 5.2.4			.

	5.2.3. Сформулируйте и докажите теорему косинусов для треугольника,
натянутого на векторы x и		y произвольного евклидова пространства.
	5.2.4. Докажите, что в произвольном треугольнике евклидова простран-
ства:
а)	длина каждой стороны не превосходит суммы длин двух других сторон;
б )	длина каждой стороны не меньше, чем абсолютная величина разности длин
	двух других сторон.
	5.2.5. Докажите, что в параллелограмме, натянутом на векторы x и			y ,
сумма квадратов длин диагоналей равна сумме квадратов длин сторон.
	5.2.6. Докажите, что в евклидовом пространстве L :
а)	нулевой векторединственный, который обладает тем свойством, что он ор-
	тогонален ко всем векторам пространства;
б )	если равенство a, x	b, x справедливо для любого вектора x L ,		то
	a b .
	5.2.7. Докажите, что если x, y, , z - ортогональная система векторов,			то
для любых чисел , , ,		система векторов x, y, , z также будет ортого-
нальна.
	5.2.8. Докажите, что если вектор x ортогонален к каждому из векторов
y1 , y2 , , ym , то он ортогонален и к любой линейной комбинации этих векто-
ров.

5.2.9. Докажите, что ортогональная система ненулевых векторов линейно независима.

5.2.10. Применив процесс ортогонализации, найдите ортонормированный базис в пространстве M2 R многочленов степени не более двух, взяв за ис-

ходный базис многочлен дано формулой:

1, t, t	2

, если скалярное произведение многочленов за-

а) б )



	1

f , g		f	t	g t	dt;
	1

f, g 0 0 1 1 2

5.2.11.В пространстве

, если

Mn R

				0	1	2		2
f	t				t		t		, g t

многочленов степени не

	0
	0

более

1t n

2t	2	.

задайте

скалярное произведение так, чтобы базис

ным.

	t	2		t	n
1,t,			, ,
	2!			n!

стал ортонормирован-

		5.2.12. Пусть			R	4	-	арифметическое

произведение определено формулой
	x, y						2		2	2	2	2	3
			1 1	1 2				1

пространство, в котором скалярное

	2	2	3		4			3	2		4
3	2	3	3	3	4	4		3	4		4

где x 1, 2 , 3 , 4 , y 1, 2 , 3 ,

Применив процесс ортогонализации,

4 - произвольные векторы из	R	4	.

найдите ортонормированный базис про-

странства R		4	, взяв за исходный базис:
странства R			, взяв за исходный базис:
а) e	1,0,0,0 ,			e	0,1,0,0 , e			0,0,1,0 ,	e
1				2		3			4
б) e	1, 1,0,0 , e					0,1, 1,0 ,	e	0,0,1, 1 ,
1				2			3

0,0,0,1 ;
e	1,0,0,1
4

R	n

В дальнейшем предполагается, что

скалярное произведение векторов

в арифметическом

1 , 2 , , n и

пространстве

	1		2		n
		,		, ,

задано формулой
		1	1	2
	x, y

	n
n


5.2.5

5.2.13. Убедитесь, что векторы x1, x2 ортогональны, и дополните систему

x1, x2	до ортогонального базиса, если
а) x	1, 2,2, 3 ,													x		2, 3,2,4 ;
1															2
б) x1 111,,,2 ,											x2			1,2,3, 3 ;
в) x	1, 2,1,3 ,											x				2,1, 31, ;
1	1, 11,, 3 ,												2		4,15,,0 .
г) x	1, 11,, 3 ,												x		4,15,,0 .
1													2
5.2.14. Дополните систему																								x1		, x2				до ортонормированного базиса, если
а) x				11			,			2		,	2			x						2			,		14			,		1
а) x							,					,			,	x									,					,			;
1				15						15			3				2					15					15
				15						15			3									15					15					3
		2			1			2								1			2		2
б) x1				,		,				,		x2						,		,			;
б) x1				,		,				,		x2						,		,			;
			3 3 3													3 3						3
		1				1				1				1								1			1			1			1
в) x1				,					,		,				,	x2								,		,			,				;
в) x1				,					,		,				,	x2								,		,			,		2		;
		2 2 2												2								2 2 2									2

5.2.15. Применяя процесс ортогонализации, постройте ортогональный ба-

зис линейной оболочки						x1 , x2 , , xk , если:
а) x	2,3, 4, 6 ,		x			18,, 2, 16 ,		x 12,5, 14,5 , x 311,,4, 7 ;
1	1,1, 1, 2 ,		2		5,8, 2, 3 ,				3			4
б) x	1,1, 1, 2 ,	x			5,8, 2, 3 ,		x		3,9,3,8 ;
1	2,1,3, 1 , x		2				3
в) x	2,1,3, 1 , x		7,4,3, 3 , x					11,, 6,0 , x			6,7,7,8 ;
1	2					3				4
г) x	11,, 1, 2 ,	x		2,1511,, ,			x		0,3,3,7 ,	x		3, 3, 3, 9 .
1			2				3			4

§ 5.3. Ортогональное дополнение. Ортогональные суммы подпространств

Два подпространства называются ортогональными, если каждый вектор одного подпространства ортогонален каждому вектору другого подпространства . Ортогональность подпространств L1 и L2 обозначается L1 L2 .

Для того чтобы вектор

был ортогонален к подпространству

L	,
1

необхо-

димо и достаточно, чтобы он был ортогонален ко всем векторам какого-либо

базиса подпространства

L1 .

Для того чтобы два подпространства были ортогональными, необходимо и достаточно , чтобы каждый вектор какого-либо базиса одного подпространства был ортогонален ко всем векторам какого-либо базиса дру-

гого подпространства.
Сумма S подпространств	L1, L2 , , Lm называется ортогональной и обо-
значается S L1 L2 Lm ,	если подпространства попарно ортогональны.
Ортогональная сумма ненулевых подпространств всегда является прямой
суммой.
Совокупность всех векторов, ортогональных к линейному подпростран-
ству L1 евклидова пространства L,		называется ортогональным дополнением
подпространства L и обозначается		L .
1		1

Евклидово пространство

есть ортогональная сумма любого своего ли-

нейного подпространства L1
нейного подпространства L1			и его ортогонального дополнения L1 , т.е.
	L L L .			5. 3.1
	1	1
	Любой вектор x из евклидова пространства L всегда можно представить,
причём единственным образом, в виде
	x g h,
	x g h,			5. 3.	2
где	g принадлежит некоторому подпространству L1 , h ортогонален к L1 .				Век-
тор g называется ортогональной проекцией вектора				x на подпространство
L1,	а h - перпендикуляром,		опущенным из x на L1 .

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.03.2016780.58 Кб10Глава 2.pdf
#
11.03.2016416.27 Кб9Глава 2.pdf
#
11.03.2016546.03 Кб8Глава 3,4.pdf
#
11.03.2016719.99 Кб7Глава 3.2.pdf
#
11.03.2016746.33 Кб8Глава 3.pdf
#
11.03.2016911.85 Кб7Глава 5.pdf
#
11.03.2016660.06 Кб5Глава 6.pdf
#
11.03.2016540.54 Кб7Глава 8.pdf
#
23.09.2019497.15 Кб8Главная Шпора ТФКП теория.doc
#
27.03.20151.92 Mб123Голуб курсач.doc
#
27.03.20151.69 Mб20Горин С.А. - НЛП. Техники россыпью [2004].doc