Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Глава 3,4

.pdf

Скачиваний:

Добавлен:

11.03.2016

Размер:

546.03 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

4Пусть P(x) = x + tg x − sin 2x ,

Q(x) = ln (1+ x) - sin x , S (x) = 1+ x4 - cos x + sin (x2 / 2).

1.P(x) = x + tg x - sin 2x = 53 x3 + o(x3 ).

2.Q(x) = (x + o(x))- (x + o(x2 ))= o(x) ;

öö

Q (x) = ç x -

+ o

÷÷

- ç x -

+ o(x4 )÷

è 2

øø

= -

+ o(x

) +

+ o(x

) = -

+ o(x

ö1+1 öö

S (x) = ç1

+ o(x4 )

- (1- o(x0

+1 ))- ç

+ oç

÷÷

è 2

÷÷

øø

+ o(x

)+ o(x) -

+ o(x

) = o(x);

S (x) = çæ1+

+ o(x4 )÷ö - çæ1-

+ o(x2+1 )÷ö - çæ

+ o(x4 )÷ö =

ø è

=x4 + o(x4 )- o(x3 )+ o(x4 )= o(x2 ); 2

S (x)

= çæ1+

+ o(x4 )÷ö

- çæ1-

- o(x4+1 )÷ö -

çæ

+ o(x4 )÷ö

11x

+ o(x

)

+ o(x

)- o

) =

+ o(x

Следовательно,

o(x

)

+ o(x2 )

- 1 +

- 1

)

+ 0

ln 1+ x

- sin x

lim

(

= lim

= ¥ ;

x + tg x - sin2x

5 1

x→0

x→0 5

x→0

3 x + o(x )

3 x + o(x)

æ x2 ö

11x4

+o(x

)

11x

+ o(x)

1+ x

-cos x +sin ç

lim

=lim

;

5 x3

+o(x3 )

o(x3 )

x→0

+ tg x -sin 2x

x→0

x→ 0

ç 5

3 +

è 3

lim

= lim

= -2 ;

ln (1+ x) - sin x

+ o(x2 )

o(x2 )

x→0

x→0 -

x→0

- 2

+ o(x

)

o(x2 )

ln (1+ x) - sin x

= lim

2 +

lim

= lim

= ¥ .3

x→0

Если необходимо разложить функцию, аргументом которой так- же является функция, требующая разложения, то сначала определя- ется количество слагаемых для аргумента, а потом для самой функ- ции выписываются слагаемые, содержащие требуемую степень.

П р и м е р 3.23. Вычислим предел lim sinsin tg(2x2 ) .
x→0	ln cos(3x)

4Запишем асимптотическое разложение числителя, пользуясь

асимптотическими формулами для синуса и тангенса и свойствами символа «o малое»:

sinsin tg(2x2 ) = sinsin(2x2 + o(2x2 ))=

=sinsin (2x2 + o(x2 )) = sin(2x2 + o(x2 )+ o(2x2 + o(x2 )))=

=sin(2x2 + o(x2 )) = 2x2 + o(x2 )+ o(2x2 + o(x2 ))= 2x2 + o(x2 ).

Выведем теперь асимптотическое разложение знаменателя, ис- пользуя асимптотические формулы для косинуса и логарифма:

öö

lncos(3x) = ln ç1-

( ) + o((3x)2 )÷ = ln ç1 + ç -

+ o(x2 )÷÷ =

è 2

øø

= ç

+ o(x2 )÷

+ oç -

+ o(x2 )÷ =

=- 92x2 + o(x2 )+ oæç - 92x2 ö÷ = - 92x2 + o(x2 ).

èø

Таким образом, данный предел равен

sinsin tg(2x2 )

2x2

+ o(x2 )

2 +

o(x2 )

lim

= lim

= -

lncos(3x)

9x2

+ o(x2 )

o(x2 )

x→0

x→0 -

x→ 0

П р и м е р 3.24. Вычислим предел lim							2 -			4 + x6						.
П р и м е р 3.24. Вычислим предел lim							2		(				)			.
				x→0 esin x					(			- x2	)	-1
				x→0 esin x				+ ln 1				- x2		-1
				æ				æ				öö
	x	6			1 x	6			x		6				x	6	+ o(x6 ).
42 - 4 + x6 = 2 - 2 1+		6				6					6					6
			= 2 - 2	ç1+				+ oç				÷÷ = -

					2 4				4
4				è	2 4			è	4			øø		4

Так как числитель является бесконечно малой функцией шестого порядка, то и знаменатель необходимо разложить до шестого порядка:

exp{sin x2} = exp íx2

+ o(x6 )ý =

=1+ ç x2 -

+ o

(x6 )÷

ç x2 -

+ o

(x6 )÷ +

ææ

ç x2 -

+ o(x6 )÷

+ o

ç x2

+ o

(x6 )÷

÷ =

3!è

(x4 + o(x6 ))

(x6

+ o(x6 ))+ o(x6 ) =

=1+ ç x2 -

+ o

(x6 )÷

+ o(x

) =1+ x

+ o(x

);

=1+ x

÷ x

Q(x) = esin x

+ ln(1- x2 )

-1 = ç1+ x2

+ o(x6 )÷ +

(-x

)

(-x

)

-x

+ o((

-x

)

)÷

-1= -

+ o(x

+ o

(x6 )

Следовательно,

lim

2 - 4 + x6

= lim

sin x2

(

)

-1

+ o(x

)

x→0

+ ln 1- x

x→0

З а м е ч а н и е .

Если

в вышеописанном

примере,

раскладывая

esin x2 , взять

sin x2 = x2 + o(x2 ),

то, сколько бы мы ни взяли потом слагаемых для экспоненты, мы потеряем величину шестого порядка малости. Если же взять

x6 x10

sin x2 = x2 - 3! + 5! + o(x10 ),

то даже при одном слагаемом в экспоненте видно, что величина x10

не может дать вклад в бесконечно малую шестого порядка. Итак, в

качестве аргумента необходимо взять на функцию

sin x2 = x2 - x3!6 + o(x6 ).

Теперь для экспоненты необходимо взять три слагаемых, так как x2 - x3!6 + o(x6 ) = o(x2 )+ x2 ;

ö2

ç x2

+ o(x6 )÷

= x4 + ç

÷ + (o(x6 ))

è 3!

+ 2çæ x2o(x6 )- x2

o(x6 )÷ö = o(x4 )+ x4 .

Аналогично,

æç x2 - x3!6 + o(x6 )ö÷ = o(x6 )+ x6 ; è ø

æç x2 - x3!6 + o(x6 )ö÷ = o(x8 )+ x8 . è ø

Заменять функцию на эквивалентную ей можно только в том случае, если она является множителем для всего выражения, стоя- щего под знаком предела.

x ö

sin3 x

П р и м е р 3.25. Вычислим предел limçln (e + x) -

x→0

e ø

öü

lnçln (e + x) -

÷ï

øï

(e + x) -

4Пределы lim

sin x

либо

çln

expílim

sin

x→0

ïx→0

оба существуют и равны, либо оба не существуют:

x ö

lnç ln(e + x) -

ç1

+ ln ç1+

÷ -

éзамена числителяù

e ø

lim

= lim

= ê

ú =

sin

x→0

ëна экв. функцию û

æ x

ö2

(

)

ln ç1+

÷ + o(x2 )-

2e2

= lim

è e

= lim

= ¥ .

sin3 x

x→0

100

Так как

o(x2 )

2e2

lim

= -¥ ,

lim

= +¥ ,

то

x→0+

x→0−

x ö

(e−∞ )= 0,

= (e+∞ )= +¥ ,

sin3 x

lim ç ln(e + x) -

lim

çln(e + x) -

x→0+ è

e ø

x→0−

а значит, искомый предел не существует.3

x→+0 (

(

)

sin x .

П р и м е р 3.26. Вычислим предел lim

e + x

-1

4Пределы

lim (sin x ×ln (ln(e + x) -1))

lim

(ln(e + x) -1)sin x

и exp

x→+0

{x→+0

}

либо оба существуют и равны, либо оба не существуют:

lim

(

sin x × ln

(

e + x

)

- 1

= lim

æ sin x × ln

æln e + ln æ1 +

x ö

-1ö

ö =

x→+0

))

x→+0

e ø

x öö

ç lnln

ç1+

e ø

× x ÷

lim

ç x × lnln

ç1+

÷÷

= lim

× lnç1

= 0.

x ö

x→+0

øø

x→+0

ç1

x→0

(

)

(

e ø

)

Следовательно,

lim

e + x

-1 sin x

=1.3

3.7. АСИМПТОТЫ

(

)

Пусть S Î

{

}

и функция

определена в окрестности S .

+¥, - ¥

Прямая y = ax + b называется асимптотой графика функции f (x)

при x ® S , если существуют такие числа a и b , что

lim é f (x) - (ax + b)ù = 0.		(3.11)
x→S ë	û

При a ¹ 0 асимптоту y = ax + b называют наклонной, а при a = 0 асимптоту y = b называют горизонтальной.

З а м е ч а н и е . Иногда вместо выражения «асимптота графика функции» говорят «асимптота функции».

101

Геометрический смысл асимптоты

Асимптота может быть определена как прямая, расстояние до которой от графика функции стремится к нулю, когда точка «стре- мится, оставаясь на графике, в бесконечность» при x → S ,

S Î{+¥,-¥} .

Теорема 3.6. Для того чтобы прямая y = ax + b была наклонной

асимптотой графика функции			f (x) при x → S , необходимо и дос-
таточно, чтобы
	f (x)			ë	(		)	û
lim	x	= a ¹	0 и lim é f			x		- axù = b .	(3.12)
x→S	x		x→S

Теорема 3.7. Для того чтобы прямая y = b была горизонтальной

асимптотой графика функции	f (x)				при x → S , необходимо и дос-
таточно, чтобы		(		)
x→S			x		= b .	(3.13)
lim f

Пусть функция f (x) определена в некоторой окрестности точки x0 (быть может, односторонней) и пусть выполнено хотя бы одно из

условий: lim f (x) = ¥ или	lim f (x) = ¥. Тогда прямая x = x0
x→x0 +0	x→x0 −0
называется вертикальной асимптотой графика функции f (x).
Теорема 3.8. Пусть x = x0	– предельная точка области определе-

ния функций p(x) и q(x). Тогда, если q(x0 ) = 0 , p(x0 ) ¹ 0 , то гра-

фик функции f (x) = qp((xx)) имеет вертикальную асимптоту x = x0 .

102

Глава 4. НЕПРЕРЫВНЫЕ ФУНКЦИИ

4.1. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ

Функция

(x) : X ® ¡ называется непрерывной во внутренней

точке x0 X ,

если выполнено одно из следующих эквивалентных

условий:

$d = d(e) > 0 "x Î X

x - x0

< d Þ

f (x)- f (x0 )

< e ;

1) ε > 0

x→x0

(

)

= f

(x→x0

)

(

0 )

;

lim f

lim x

f (x) = f (x0 )+ a(x),

где

a(x) – бесконечно малая функция

при x → x0 , a(x0 ) = 0;

любая ε-окрестность точки f (x0 ) содержит образ (при ото-

бражении f

) некоторой окрестности точки x0 .

Функция f (x): X ® ¡ называется

– непрерывной справа в точке x0 X , если

f (x0 +) = lim f (x) = f (x0 );

x→x0 +

– непрерывной слева в точке x0 X , если

f (x0 -) = lim f (x) = f (x0 ).

x→x0 −

З а м е ч а н и е 1 . Понятия «непрерывна справа» («непрерывна слева») определены только для функции, определенной в некоторой правой (левой) окрестности точки x0 и в самой точке x0 .

З а м е ч а н и е 2 . Определения «непрерывна справа» и «непре- рывна слева» даны на базе второго определения непрерывности.

Аналогично эти понятия можно дать на базе любого из трех других определений.

Теорема 4.1. Для того чтобы функция f (x) была непрерывна в

точке x0 , необходимо и достаточно, чтобы она была непрерывна справа и слева.

4Справедливость теоремы следует из определения непрерывно- сти и леммы 3.13

103

Пусть функция y = f (x) определена на некотором интервале (a,b). Фиксируем любое значение x0 Î(a,b) и дадим аргументу x0 произвольное приращение x такое, что x0 + Dx Î(a,b). Приращением функции y = f (x) в точке x0 , соответствующим приращению аргумента Dx , называют число

Dy = f (x0 + Dx) - f (x0 ) .

З а м е ч а н и е . Вместо интервала (a,b) можно рассматривать сег- мент [a,b] , луч и всю числовую прямую.

Теорема 4.2 (разностная форма условия непрерывности). Для того чтобы функция y = f (x) была непрерывной в точке x0 , необ-

ходимо и достаточно, чтобы приращение y этой функции в точке x0 , соответствующее приращению аргумента Dx , было бесконечно малым при Dx ® 0 , то есть

		ë	( 0		)	- f	( 0 )û
lim Dy = lim é f			x + Dx			- f	x	ù = 0 .
x→0	x→0
4По определению, функция f (x)				непрерывна в точке x0 , если
	lim f (x0 + Dx) = f (x0 ).							(4.1)
	x→0

Существование предельного значения (4.1) эквивалентно тому,

ë	( 0	+ Dx	)	- f	( 0 )û		является бесконеч-
что функция é f	x				x	ù аргумента Dx

но малой при Dx ® 0 .3

За м е ч а н и е 1 . Аналогично определяется разностная форма не- прерывности справа (слева).

За м е ч а н и е 2 . Хотя для непрерывных функций при бесконечно малом приращении аргумента, приращение функции также бесконеч- но малая величина, но в общем случае судить о величине приращения функции по величине приращения аргумента нельзя (возможны все

три случая: Dy = o(Dx), Dx = o(Dy), y : x при Dx ® 0 ).

Свойства непрерывных функций

Пусть f и g – непрерывные в точке x0 функции, тогда для них

выполняются следующие свойства.

1. α, β ¡ αf + βg – непрерывна в точке x0 .

2.f × g – непрерывна в точке x0 .

3.f / g – непрерывна в точке x0 , если g (x0 ) ¹ 0.

104

4.Если f (x0 ) ¹ 0, то функция f (x) сохраняет знак в некоторой окрестности точки x0 .

5.f (x) ограничена в некоторой окрестности точки x0 .

4Все свойства являются следствиями соответствующих свойств пределов3

Теорема 4.3 (о непрерывности композиции). Пусть функция y(x) непрерывна в точке x = x0 , а функция x(t) – в точке t = t0 , то-

гда сложная функция y(x(t)) является непрерывной в точке t = t0 ,

или, что то же самое, если lim x(t) = x0 Î ¡ и lim y(x) = y0 , то

t→t0

x→x0

lim y (x(t)) = y0

= lim y (x) ,

t→t0

x→x0

где x(t0 ) = x0 , y(x0 ) = y0 .

4Так как x(t) непрерывна в точке t = t0 , то

"ex > 0 $dt (ex ) > 0 "t

t - t0

< dt Þ

x(t )- x (t0 )

< ex .

(4.2)

Аналогично, из непрерывности y(x) в точке x = x0 следует, что

"ey > 0 $dx (ey ) > 0 "x

x - x0

< dx Þ

y(x) - y(x0 )

< ey .

(4.3)

Взяв в формуле (4.2) ex = dx (ey ), получим, что

"ey > 0 $dt (ex ) > 0 "t t - t0 < dt Þ y (x(t)) - y(x(t0 )) < ey ,

что и требовалось доказать.3

4.2. ТОЧКИ РАЗРЫВА

Пусть x0 – предельная точка области определения функции f .

Тогда если функция f не является непрерывной в точке x0 , говорят,

что функция f разрывна в точке x0 , а саму точку	x0		называют
точкой разрыва функции f .
З а м е ч а н и е . Согласно определению, функция y =			не явля-
З а м е ч а н и е . Согласно определению, функция y =		x	не явля-
ется ни непрерывной, ни разрывной точке x0 = −2.

Устранимый разрыв. Точка x0 называется точкой устранимого разрыва функции f (x), если предельное значение функции в этой точке существует, но функция f (x) или не определена в точке x0 ,

или f (x0 ) ¹ xlimx f (x) (рис. 4а,б).

→ 0

105

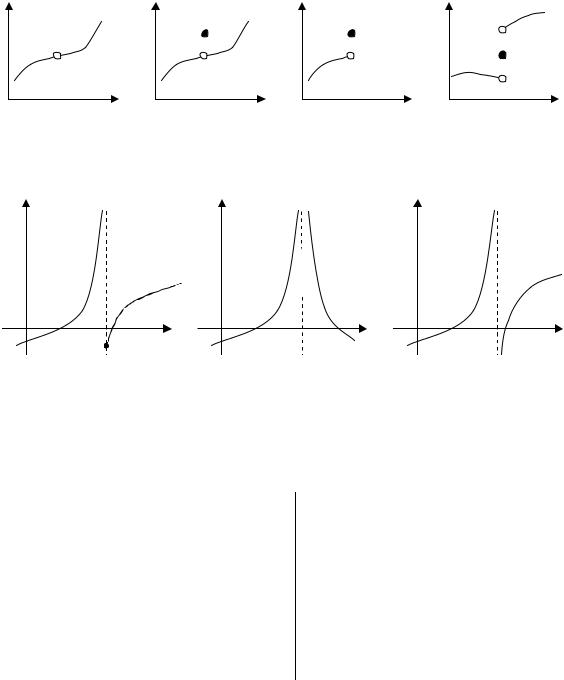
Разрыв 1-го рода. Точка x0	называется точкой разрыва 1-го ро-
да, если в этой точке функция	f (x) имеет конечные, но не равные
друг другу правое и левое предельные значения (рис. 4в,г).
Разрыв 2-го рода. Точка x0	называется точкой разрыва 2-го рода,
если в этой точке функция f (x)	не имеет, по крайней мере, одного из

односторонних предельных значений или если хотя бы одно из одно- сторонних предельных значений равно бесконечности (рис. 5а-в).

Y Y Y Y

x0	X	x0	X	x0	X	x0	X
а		б	Рис. 4	в		г
			Рис. 4
Y		Y			Y

x0	X	x0	X	x0	X
	а		б		в

Рис. 5

Теорема 4.4 (о точках разрыва монотонной функции). Пусть f (x) монотонна на отрезке [a,b] . Тогда она может иметь на этом

отрезке разрывы только первого рода. Более того,

если	f (x) не убывает, то
lim	f (x) = inf	f (x) = l2 ,
x→x0 +	x [a,b]
	x>x0
lim	f (x) = sup	f (x) = l1,
x→x0 −	x [a,b]

x<x0

l1 ≤ f (x0 ) ≤ l2.

если f (x) не возрастает, то

lim	f (x) = sup	f (x) = l1	,
x→x0 +	x [a,b]
	x>x0
lim	f (x) = inf	f (x) = l2	,
x→x0 −	x [a,b]
	x<x0

l1 ≤ f (x0 ) ≤ l2.

106

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
27.03.2015148.54 Кб7глава 2.docx
#
11.03.2016478.69 Кб20Глава 1.pdf
#
27.03.2015184.32 Кб10Глава 10.doc
#
11.03.2016780.58 Кб10Глава 2.pdf
#
11.03.2016416.27 Кб9Глава 2.pdf
#
11.03.2016546.03 Кб8Глава 3,4.pdf
#
11.03.2016719.99 Кб7Глава 3.2.pdf
#
11.03.2016746.33 Кб8Глава 3.pdf
#
11.03.2016911.85 Кб7Глава 5.pdf
#
11.03.2016660.06 Кб5Глава 6.pdf
#
11.03.2016540.54 Кб7Глава 8.pdf