Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Глава 3,4

.pdf

Скачиваний:

Добавлен:

11.03.2016

Размер:

546.03 Кб

Скачать

☆

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

П р и м е р 3.3. Докажем, что lim (xln x) = -0.

x→+0

f ′(x) = ln x +1 < 0

4Рассмотрим функцию

f (x) = xln x . Так как

при x Î(0, e−1 ),

то на интервале x Î(0, e−1 ) функция убывает, а зна-

чит,

lim

(

)

sup

(

)

. Так как

"x Î

(

0,e−1

)

(

)

= xln x < 0,

x→0+

x (0,e−1 )

то

sup

(x) £ 0 . Таким образом, мы доказали существование ко-

x (0,e−1 )

f (x) , а значит, и конечного предела

lim f (x) .

нечного

sup

x (

0,e−1 )

x→+0

Рассмотрим

последовательность

аргументов

функции xn =

n > 1. При

n → ∞ xn → + 0, а соответствующая ей последователь-

ность значений функции

f(xn ) = 1n ln 1n = - lnnn ® -0 .

Всилу определения предела функции по Гейне, получаем, что

lim (xln x) = -0.3	(3.2)
x→+0

Теорема 3.2 (о пределе композиции функций). Пусть для

функций y(x)	и x(t)	существуют пределы lim x(t) = Sx и
		t→St

lim y(x) = Sy , причем если Sx Î¡,	то в некоторой окрестности пре-
x→Sx
дельного значения St "t ¹ St x(t) ¹ Sx . Тогда
lim y (x(t )) = Sy	= lim y (x).	(3.3)
t→St	x→Sx

4Заметим, что если Sx ¡, то существование предела lim y (x)

x→Sx

(даже конечного) не означает, что функция y (x) определена в точке x = Sx , поэтому необходимо потребовать, чтобы в некоторой окре- стности предельного значения St функция x(t) не принимала зна- чения Sx (это требование необходимо только для конечного Sx ).

Пусть {tn} – произвольная последовательность значений аргу- мента сложной функции, сходящаяся к St при n → ∞ . Так как

lim x(t) = Sx Î ¡, то, согласно определению предела по Гейне, соот-
t→St	= x(tn )
ветствующая последовательность значений этой функции xn

сходится к Sx .	Последовательность {xn } для функции	y( x) –	схо-
дящейся к	Sx последовательность аргументов,	а так	как
lim y(x) = Sy ,	очевидно, что последовательность yn	= y ( xn )	схо-
x→Sx
дится к Sy .

Итак для произвольной сходящейся к St последовательности аргу- ментов {tn } соответствующая последовательность значений

yn = y (x(tn )) сложной функции сходится к Sy . Поэтому, согласно оп-

ределению предела по Гейне, lim y(x(t)) = Sy .3

t→St

П р и м е р 3.4. Вычислим предел lim

ln x .

x→+∞

4Перейдя от функции y(x) = ln x к функции y (t) =

ln (1/ t)

, где

1/ t

t = 1/ x, в силу теоремы 3.2, получим

ln x

(-t lnt) = +0. 3

lim

= lim

çt ln

= lim

(3.4)

x→+∞

t→+0

Теорема 3.3 (теорема Коши о существовании предела функ-

ции в точке). Пусть x0 ¡ – предельная точка множества X и f : X → ¡. Конечный предел функции f в точке x0 существует то- гда и только тогда, когда

f (x2 ) - f (x1 )

"e > 0 $d > 0 "x1, x2 Î B(x0 ,d)I A

< e .

4Необходимость. Пусть

lim

f (x) = p Î ¡. Тогда, по определе-

x→x0

нию предела, ε > 0

δ > 0 такое, что "x Î B(x0 ,d)I A выполняет-

ся неравенство

f (x) - p

< e

. Следовательно,

,d)I A

f (x1 ) - p

< e

"e > 0

$d > 0

ï"x1 Î B(x0

,d)I A

f (x2 ) - p

ï"x2 Î B(x0

< e

(x1 ) - p

Û "e > 0

2 Þ

$d > 0 "x1, x2 Î B(x0 ,d)I A í

ïï

(x2 ) - p

< e

Þ "e > 0

$d > 0 "x1, x2 Î B(x0 ,d)I A

f (x2 ) - f (x1 )

f (x2 ) - p

p - f (x1 )

< e

+ e

= e.

Достаточность. Воспользуемся определением предела по Гей- не, то есть докажем, что какую бы мы ни взяли последовательность аргументов, последовательность соответствующих значений функ- ции будет сходиться к некоторому фиксированному числу.

Достаточно доказать, что для двух произвольных последова- тельностей аргументов {yn } и {zn} таких, что

1) lim yn = x0

и "n Î ¥ yn

¹ x0 , yn Î A;

n→∞

и n ¥ zn

¹ x0 , zn Î A ,

2) lim zn = x0

n→∞

пределы соответствующих последовательностей значений функций

равны, то есть lim f ( yn ) = lim f

(zn ).

n→∞

} и {zn} образуем новую:

Из последовательностей {yn

{

1 1

, z

,..., y

, z

}

(3.5)

y , z , y

,... .

Очевидно, что для этой последовательности

lim x

= x

и "n Î ¥ x

¹ x , x Î A .

n→∞

Докажем,

что последовательность { f (xn )}

сходится. Пусть e > 0

задано, а d > 0

выбрано согласно условию теоремы, то есть так, чтобы

f (x2 )- f (x1 )

"x1, x2 Î B(x0 ,d)I A

< e .

(3.6)

Так как lim x

= x , то по определению предела для d > 0

(выбран-

n→∞

ного ранее) $M "n ³ M

xn - x0

< d. Тогда

"m ³ M "n ³ M xm Î B(x0 ,d)I A и xn Î B(x0 ,d)I A,

и, учитывая (3.6),

f (xm ) - f (xn )

< e .

Таким

образом, последова-

тельность { f (xn )} фундаментальна, а значит,

она сходится к неко-

торому числу p ¡, то есть lim f

(xn ) = p .

n→∞

Из (3.5) следует, что { f ( yn )}

и { f (zn )}

– подпоследовательно-

сти последовательности значений функции { f (xn )}, а значит

lim f ( yn )

= lim f

(zn ) = lim f (xn ) = p .3

n→∞

3.3. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ

Первый замечательный предел: lim sin x = 1.

x→0

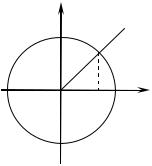
Докажем,

что при

выполняется

0 < x < 2

неравенство sin x < x < tgx .

ON = cos x,

MN = sin x ,

AB = tg x .

sin x,

, S

tg x .

OMA

сект. OMA

OAB

Так как S OMA < Sсект. OMA < S OAB (рис. 3), то

Рис. 3

sin x < x < tgx .

p ö

sin x

> 0, получим

Учитывая, что "x Îç

1 <

или cos x <

sin x

<1,

(3.7)

sin x

cos x

а значит,

lim cos x £ lim

sin x

£ lim1; следовательно, lim

sin x

=1.

x→+0

Пусть

положив y = −x ,

на основании дока-

x Îç

÷. Тогда,

занного выше неравенства (3.7):

cos y <

sin y

< 1.

(3.8)

Так как cos y и

sin y

– четные функции, то из (3.8) следует, что

sin x

cos x <

< 1.

Переходя к пределу при x → 0 − , получаем

lim cos x £ lim

sin x

£ lim1,

lim sin x

x→−0

а значит,

=1.

x→−0

Итак, lim

sin x

= lim

sin x

= 1, поэтому lim

sin x

= 1.3

x→+0

x→−0

x→0

Следствия первого замечательного предела

lim

arcsinx

4lim

arcsinx

é y = arcsinx,ù

= lim

= 13

= sin y

x→0

y→0 sin y

lim

tgx

= 1

tgx

æ sin x

4lim

= limç

÷ = 13

cos x

x→0

lim arctgx = 1

4lim

arctgx

é y = arctgx,ù

= lim

= 13

x = tg y

tg y

x→0

y→0

lim(x ×ctgx) = 1

4lim(x ×ctgx) = lim

= 13

tgx

x→0

lim

1− cos x

4lim

1- cos x

= lim

2sin

(x / 2)

x→0

= lim

2sin2 (x / 2)

x→0

4(x /2)2

Второй замечательный предел:

öx

= e .

lim

ç1+

x→∞

41°. Рассмотрим сначала случай x → +∞ . В силу монотонности

показательной функции справедливы неравенства

ö[ x]

öx

1 öx

ö[x]+1

ç1+

< ç1+

< ç1

÷ .

[x] +1

[x] +1ø

x ø

[x]ø

1 ön

= e получаем, что

Учитывая, что lim

ç1

n→∞

n ø

æ		1	ön	æ		1	ön+1
lim ç1	+		÷	= lim ç1	+		÷	= e,
		n +1				n
n→∞ è			ø	n→∞ è			ø

то есть справедливы утверждения

ï$N1 = N (e)

"e > 0 í

ïï $N2 = N (e)

	æ		1	ön
"n > N1	ç1	+		÷	- e	< e;
			n +1
	è			ø

n+1

"n > N2 æç1+ 1n ö÷ - e < e. è ø

Тогда при n > max{ N1, N2}

имеем

ön

ön+1

e - e <

ç1+

< e + e

и e - e <

ç1

< e + e.

n +1

Если x > 1+ max{N1, N2} = N , то [x] > N -1. Следовательно,

1 ö[ x]

öx

1 ö[ x]+1

x > N e - e < ç1+

< ç1

ç1

< e + e .

[x] +1ø

[x]ø

Таким образом, получили "e > 0

"x > N

öx

- e

< e, а

ç1+

значит,

lim

öx

= e.

ç1+

→+∞

2°. Рассмотрим случай x → −∞ . Положим y = −x , тогда

öx

ö− y

y -1ö− y

lim

ç1+

lim ç1

= lim

x→−∞ è

y→+∞ è

y→+∞

öy

= lim

öy

éæ

öy−1 æ

= e.

lim ç

ç1

lim

êç1

ç1

÷ú

y -1

y -

y→+∞ è y -1

y→+∞ è

y→+∞ êè

1øú

öx

Соединяя вместе 1° и 2°, получаем: lim

= e .3

ç1

x→∞

Следствия второго замечательного предела

1/ x

4lim(1+ x)

ê y =

1. lim 1+ x

= e.

1/ x

x→0

(

)

öy

= e.3

= lim

ç1+

y→∞

x→0

(

)

loga (1+ x)

4log

lim 1+ x

1/ x

2. lim

1/ x

loga

(1+ x)

→

ln a

= lim

élog

1+ x

)

= lim

x→0

a (

x→0

3. lim

ln(1+ x)

= 1.

C другой стороны

x→0

1/ x

log

lim 1+ x

)

= log

e =

ln a

x→0

(

3.4. СРАВНЕНИЕ ФУНКЦИЙ. СИМВОЛЫ ЛАНДАУ

Пусть для функций f (x) и g (x) , определенных на множестве

X , в некоторой окрестности предельного значения S множества X справедливо представление f (x) = j(x) g (x). Тогда:

Обозначение

Определение

«Функция f (x) ограничена по сравнению с

f (x) = O(g ( x))

функцией g (x) в окрестности S », если c та-

в указанной

кое, что для всех x из указанной окрестности

окрестности

выполняется неравенство

j(x)

£ c

f (x) = O* (g (x))

«Функция f (x) одного порядка с функцией

g (x) при x → S », если

при x → S

x→S

(

)

= c ¹ 0

limj

«Функции f (x) и

g (x)

эквивалентны при

f (x) : g (x)

x → S » или «функции

f (x) и g (x) асимпто-

при x → S

тически равны при x → S », если

x→S

(

)

= 1

limj

f (x) = o(g (x))

«Функция f (x) при x → S является бесконеч-

но малой по сравнению с функцией g (x)», если

при x → S

limj(x) = 0

x→S

З а м е ч а н и е 1 .

Запись x → S указывает на то, что рассматри-

ваемое свойство имеет место лишь в некоторой окрестности пре- дельного значения S (ни о каком пределе здесь речи нет).

З а м е ч а н и е 2 . Если функция g бесконечно малая и f = o(gn )

при x → S , то говорят, что функция f является бесконечно малой порядка n относительно бесконечно малой g .

З а м е ч а н и е 3 . Свойства функций «быть функциями одного по- рядка» и «быть эквивалентными функциями» являются симметрич- ным свойствами, а свойство одной функции быть «О большим» от-

носительно другой уже не симметрично. Например, x2 = O(x) при x → 0, но x ¹ O(x2 ) при x → 0.

В частном случае множество X может быть множеством нату- ральных чисел ¥, тогда при S = +∞ мы получим понятия:

– последовательности {xn } , ограниченной по сравнению с по-

следовательностью { yn } : xn = O( yn ) , n → ∞ ;

– последовательности {xn } одного порядка с последовательно-

стью { yn } : xn = O* ( yn ), n → ∞ ;

– последовательности {xn } , асимптотически равной последова-

тельности { yn } : xn : yn , n → ∞ ;

– последовательности {xn } , бесконечно малой по сравнению с последовательностью { yn } : xn = o( yn ) , n → ∞ .

При использовании равенств с символами O и o следует иметь в виду, что они не являются равенствами в обычном смысле этого слова. Так, если

a1 = o(b) при x → S , a2 = o(b) при x → S ,

то было бы ошибкой сделать отсюда заключение, что α1 = α2 , как


это было бы в случае обычных равенств. Например, при			x → 0
x2 = o(x) и x3 = o(x), но x2	¹ x3 . Аналогично, если
f + O(	f ) = g + O( f ) при x → S ,
то было бы ошибкой сделать заключение, что f		= g .
Дело в том, что один и тот же символ O(		f ) или o( f )	может

обозначать разные конкретные функции. Это обстоятельство связа- но с тем, что при определении символов O( f ) или o( f ) мы, по

существу, ввели целые классы функций, обладающих определен- ными свойствами (класс функций, ограниченных в некоторой окре-

стности точки S по сравнению с функцией f (x) , и класс функций, бесконечно малых по сравнению с f (x) при x → S ), и было бы правильнее писать не a = O( f ) или a = o( f ) , а соответственно a ÎO( f ) или a Îo( f ). Однако это привело бы к существенному усложнению вычислений по формулам, в которых встречаются сим- волы O и o . Поэтому мы сохраним прежнюю запись a = O( f ) и a = o( f ) , но будем всегда читать эти равенства только в одну сто- рону: слева направо. Например, запись a = o( f ) при x → S , озна-

чает, что функция α является бесконечно малой по сравнению с функцией f при x → S , но не означает, что всякая бесконечно ма-

лая по сравнению с f функция равна α .

Отметим, что сказанное об использовании символов O и o не исключает того, что отдельные формулы с этими символами могут оказаться справедливыми не только при чтении слева направо, но и справа налево.

Свойства символов Ландау♦

Если f = o(g ) , то f = O (g ) .

12. Если ck Î¡ , c ¹ 0 , то

Если f = O* (g ) , то g = O* ( f ) .

Отношение

является рефлек-

c ×O (g ) = O (g ),

c × o(g) = o(g ).

сивным, симметричным и транзитив-

ным.

13. O(O(g )) = O (g ),

Если f : g , то o( f ) = o(g),

o(o(g )) = o(g ),

f = O (g ) ,

f = O* (g ) ,

f - g = o( f ) , f = g + o(g ) .

O(o(g)) = o(O(g)) = o(g).

Если f = g + o(g) , то f : g .

14. h ×O (g ) = O (h × g ),

Если lim f = c ¹ 0, c Î ¡ , то f : c .

h × o(g) = o(h × g) .

x→S

Если f = O* (g ) , то

15. O(g )×O (g ) = O(g2 ),

$c Î ¡ ,

c ¹ 0 , f

: cg .

Если f : f1 и g : g1 , то

o(g )×o (g ) = o(g2 ),

f × g : f1 × g1.

O(g )× o(g ) = o(g2 ).

Если f : f1 ,

g : g1 и функции g ,

16. O (g ) + O (g ) = O (g ),

g1 не обращаются в нуль в некоторой

окрестности предельного значения S , то

o(g ) + o(g) = o(g ),

O(g ) + o(g) = O(g).

17. O(g ) - O (g ) = O(g),

10. Если b = b(x) – БМФ при x ® S , то

o(bn+ k ) = o(bn )

o(g ) - o(g ) = o (g ),

и oçæåck bk ÷ö = o(bn ),

O(g ) - o(g ) = O(g ).

где ck Î ¡ , cn ¹ 0 .

è k =n

11. Если b = b(x) – ББФ при x → S , то

o(bn ) = o(bn+k )

и oçæåckbk ÷ö = o(bm ),

где ck Î ¡, cm ¹ 0.

è k =n

f = f (x), g = g (x) , h = h(x) , s = s (x).

♦ Во всех свойствах x → S и

Основные асимптотические разложения

∞ xn

ån=0

= 1+ x +

... +

+ o(x

)

sin x = å(−1)n

= x − x

+ x

+ ... + (−1)

2n+1

+ o(x2n+2 )

∞

(2n +1)!

n=0

(2n +1)!

3! 5!

cos x = å(−1)n

= 1− x

+ x

+ ... + (−1)

+ o(x2n+1 )

∞

(2n)!

n=0

(2n)!

2! 4!

1+ x

)

= ∞

−1

n+1

= x −

− ... +

(

−1

n+1

+ o

(

)

(

å(

)

n=1

(1+ x)α =

∞

α(α −1)L(α − (n −1))

1+ å

xn =

n=1

(

α(α −1)L(α − (n −1))

α −1

=1+ αx +

)

+ ... +

xn + o(xn )

Если

функция

f (x)

заменяется

функцией

g (x),

то разность

f (x) - g (x)

называется абсолютной погрешностью,

а отношение

f (x) - g (x)

– относительной погрешностью сделанной замены.

f (x)

Если

lim é f (x)- g (x)

ù = 0, то говорят,

что

g (x) приближает

x→S

или аппроксимирует функцию f (x) при x → S .

З а м е ч а н и е .

Для функций, эквивалентных заданной, не только аб-

солютная погрешность

f (x) - g (x), но и относительная погрешность

f (x) - g (x)

стремится к нулю при x → x . В этом смысле функции,

f (x)

эквивалентные заданной, приближают ее лучше, чем другие.

П р и м е р 3.5. Функции ax являются бесконечно малыми при x → 0, так же как и sin x , а поэтому абсолютные погрешности при замене sin x каждой из них стремятся к нулю при x → 0, то есть

lim(sin x - ax) = 0. Но лишь для одной из всех перечисленных функ-
x→0
ций, а именно для g (x) = x , относительная погрешность при замене
sin x этой функцией будет стремиться к нулю при x → 0, так как
	sin x - ax	æ	ax ö
lim		= lim ç1-		÷ =1- a .
	sin x
x→0		x→0 è	sin x ø

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
27.03.2015148.54 Кб7глава 2.docx
#
11.03.2016478.69 Кб20Глава 1.pdf
#
27.03.2015184.32 Кб10Глава 10.doc
#
11.03.2016780.58 Кб10Глава 2.pdf
#
11.03.2016416.27 Кб9Глава 2.pdf
#
11.03.2016546.03 Кб8Глава 3,4.pdf
#
11.03.2016719.99 Кб7Глава 3.2.pdf
#
11.03.2016746.33 Кб8Глава 3.pdf
#
11.03.2016911.85 Кб7Глава 5.pdf
#
11.03.2016660.06 Кб5Глава 6.pdf
#
11.03.2016540.54 Кб7Глава 8.pdf