
Глава 8
.pdf8.5.4*. Частные случаи интегрирования тригонометрических
дифференциалов
Помимо стандартных методов интегрирования функций вида R(cos x,sin x), описанных выше, существуют и специальные, позво- ляющие значительно сократить вычисления.
1. ò |
a sin x + b cos x |
dx , |
a1 |
b1 |
¹ 0 . |
||
1 |
1 |
|
|
||||
asin x + bcos x |
a |
b |
|||||
|
|
|
|||||
Представим числитель в виде линейной комбинации знаменателя и его производной
a1 sin x + b1 cos x = A(asin x + bcos x) + B(asin x + bcos x)¢ = = ( Aa - Bb)sin x + ( Ab + Ba)cos x.
Коэффициенты A, B этого разложения могут быть найдены из
системы уравнений
ìa1 = Aa - Bb,
íîb1 = Ab + Ba.
Тогда ò |
a1 sin x + b1 cos x |
dx = |
|
|
|
|
|
|
|
|
|
|||||
asin x + bcos x |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
asin x + bcos x |
|
|
(asin x + bcos x)¢ dx |
|
|||||||||
|
|
= Aò asin x + bcos x dx + Bò |
asin x + bcos x |
= |
||||||||||||
|
|
|
|
= Ax + B ln |
|
asin x + bcos x |
|
+ C. |
|
|||||||
|
|
|
|
|
|
|
||||||||||
2. ò |
a sin x + b cos x + d |
dx , rang |
|
a1 |
b1 |
d1 |
|
= 2. |
|
|||||||
|
|
|
||||||||||||||
1 |
1 |
1 |
|
|
|
|
|
|
|
|
||||||
asin x + bcos x + d |
|
a |
b |
d |
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||
Представим числитель в виде линейной комбинации знаменате- ля, его производной и константы a1 sin x + b1 cos x + d1 =
=A(asin x + bcos x + d ) + B(asin x + bcos x + d )′ + D =
=( Aa - Bb)sin x + ( Ab + Ba)cos x + Ad + D.
Коэффициенты A, B, D этого разложения могут быть найдены из
системы уравнений
ìa1 = Aa - Bb,
ïíb1 = Ab + Ba,
ïî d1 = Ad + D.
224

Тогда ò a1 sin x + b1 cos x + d1 dx = asin x + bcos x + d
|
= |
Aò |
asin x + bcos x + d |
dx + Bò |
(asin x + bcos x + d )¢ dx |
+ |
|||||||||||||||||
|
asin x + bcos x + d |
asin x + bcos x + d |
|
|
|||||||||||||||||||
|
|
|
|
|
+Dò |
|
|
dx |
|
|
|
= |
|
|
|
|
|
|
|
||||
|
|
|
|
|
asin x + bcos x + d |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
= Ax + Bln |
|
asin x + bcos x + d |
|
+ Dò |
|
|
|
|
|
dx |
|
|
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
asin x + bcos x + d |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3. ò |
a sin2 x + b sincos x + d cos2 |
x |
dx , rang |
|
a1 |
b1 |
d1 |
|
= 2. |
||||||||||||||
|
|
||||||||||||||||||||||
1 |
1 |
|
|
|
1 |
|
|
a |
2 |
2ab |
b |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
asin x + bcos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Представим числитель в виде:
a1 sin2 x + b1 sincos x + d1 cos2 x =
=( Asin x + Bcos x)(asin x + bcos x) + D(sin2 x + cos2 x) =
=( Aa + D)sin2 x + ( Ab + Ba)sin xcos x + (Bb + D)cos2 x.
Коэффициенты A, B, D этого разложения могут быть найдены из
системы уравнений
|
|
ì a = Aa + D, |
|
|
|
|||||
|
|
ï |
1 |
|
|
|
|
|
|
|
|
|
íb1 = Ab + Ba, |
|
|
|
|||||
|
|
ï d = Bb + D. |
|
|
|
|||||
|
|
î |
1 |
|
|
|
|
|
|
|
Тогда ò |
a sin2 |
x + b sincos x + d cos2 |
x |
dx = |
|
|
|
|||
1 |
1 |
1 |
|
|
|
|
|
|||
|
asin x + bcos x |
|
|
|
|
|
||||
= ò( Asin x + Bcos x)(asin x + bcos x) dx + Dò |
|
dx |
= |
|||||||
asin x + bcos x |
||||||||||
|
|
asin x + bcos x |
|
|
dx |
|
||||
|
= Bsin x - Acos x + Dò |
|
|
|
. |
|
||||
|
asin x + bcos x |
|
||||||||
|
|
|
|
|
|
|||||
Пр и ме р 8.36. Вычислим ò 6sin2 x + 2sin xcos x + 4cos2 xdx . sin x + cos x
4Представим числитель 6sin2 x + 2sin xcos x + 4cos2 x в виде
6sin2 x + 2sin x cos x + 4cos2 x =
= ( Asin x + Bcos x)(sin x + cos x) + C (sin2 x + cos2 x).
225

Для нахождения неизвестных коэффициентов A, B,C имеем систему
ìA + C = 6, |
|
|
|
|
|
|
||||||||
ï |
|
|
= 2, |
|
|
|
|
|
|
|
|
|||
íA + B |
|
|
|
|
|
|
|
|
||||||
ï |
|
|
= 4. |
|
|
|
|
|
|
|
||||
îB + C |
|
|
|
|
|
|
|
|||||||
Решая эту систему, находим A = 5, B = −3, C = 1, поэтому |
|
|||||||||||||
ò 6sin2 x + 2sin xcos x + 4cos2 xdx = −5cos x − 3sin x + ò |
dx |
= |
||||||||||||
sin x + cos x |
||||||||||||||
sin x + cos x |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
2 |
+ t -1 |
% |
|
|
|||
= -5cos x - 3sin x + |
|
|
|
|
ln |
|
|
|
|
|
+ C , |
|
|
|
|
|
|
|
|
|
-t +1 |
|
|
||||||
2 |
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||
(см. пример 8.30).3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.6. ИНТЕГРАЛЫ ВИДА òR(sh x,ch x) |
dx |
|
|
|
||||||||||
Интегралы данного вида можно привести к интегралам, содержа- щим экспоненту, используя определение гиперболических функций:
sh x = |
ex - e− x |
, ch x = |
ex + e− x |
. |
(8.23) |
|
2 |
2 |
|||||
|
|
|
|
Предварительно исходное выражение можно попытаться упро- стить, применяя следующие гиперболические тождества.
ch |
2 |
x - sh |
2 |
x =1 |
|
|
|
sh xsh y = éch |
(x + y) |
- ch (x - y)ù / 2 |
||||||||||||||||
|
|
|
ë |
( |
|
|
|
) |
|
|
|
( |
|
|
|
û |
||||||||||
sh 2x = 2sh xch x |
|
|
|
ch xch y = éch |
x + y |
+ ch |
x - y |
ù / 2 |
||||||||||||||||||
|
ë |
|
|
|
|
|
|
|
|
|
)û |
|||||||||||||||
ch 2x = sh2 x + ch2 x |
|
|
|
sh xch y = ésh |
(x + y) |
+ sh(x - y)ù / 2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
û |
|||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
ch |
x |
|
|
|
|
|
|
|
|
|
|
|
|
sh |
= sgn x × |
ch x -1 |
|
|
|
|
= |
|
ch x +1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
Также для данных интегралов применимы подстановки, анало-
гичные |
подстановкам, |
используемым для |
интегралов |
вида |
|||||||
òR(sin x,cos x) dx . Так, например, подстановка |
t = th(x / 2), учиты- |
||||||||||
вая равенства |
|
|
|
|
|
|
|
|
|
||
|
2th (x / 2) |
1 |
+ th2 |
(x / 2) |
|
2dt |
|
|
|||
sh x = |
|
, ch x = |
|
|
|
, x = 2Arth t , dx = |
|
|
, |
||
1- th2 (x / 2) |
1 |
- th2 |
(x / 2) |
1- t2 |
|
||||||
226

сводит интеграл òR(sh x,ch x)dx к интегралу от рациональной дроби:
ò |
R(sh x,ch x)dx = 2 |
ò |
æ |
|
|
2t |
,1+ t |
2 |
ö |
|
dt |
|
|
Rç |
|
|
|
÷ |
|
. |
|||||||
1 |
2 |
2 |
|
2 |
|||||||||
|
|
è |
- t |
1- t |
|
ø1 |
- t |
||||||
Заметим, что обратные функции |
|
|
x = x(t ) |
для гиперболических |
|||||||||
подстановок t = sh x , |
t = ch x , t = th x |
могут быть получены из вы- |
|||||||||||
ражений (8.23). |
|
|
|
|
|
|
|
|
|
|
|
|
|
8.7.ИНТЕГРАЛЫ ОТ ТРАНСЦЕНДЕНТНЫХ ФУНКЦИЙ, ВЫЧИСЛЯЮЩИЕСЯ С ПОМОЩЬЮ ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ
Ктаким интегралам относятся, например, интегралы
òeαx sin (bx)dx, òeαx cos(bx)dx, |
ò xn sin(ax)dx, òxn cos(ax)dx, |
òxneαxdx, òxn ln xdx, òxn arcsin(bx)dx, òxn arccos(bx)dx, |
|
òxn arctg(bx)dx, |
òxn arcctg(bx)dx. |
Все эти интегралы вычисляются с помощью последовательного ин- тегрирования по частям. Кроме того, через интегралы
òeαx cos(bx)dx , òeαx sin(bx)dx
легко выражаются интегралы:
òsh (ax)sin (bx)dx, òch (ax)sin (bx)dx,
òsh (ax)cos(bx)dx, òch(ax)cos(bx)dx.
8.8.ИНТЕГРАЛЫ ВИДА òR(x,
 a2 ± x2 )dx , òR(x,
a2 ± x2 )dx , òR(x,
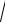 x2 − a2 )dx
x2 − a2 )dx
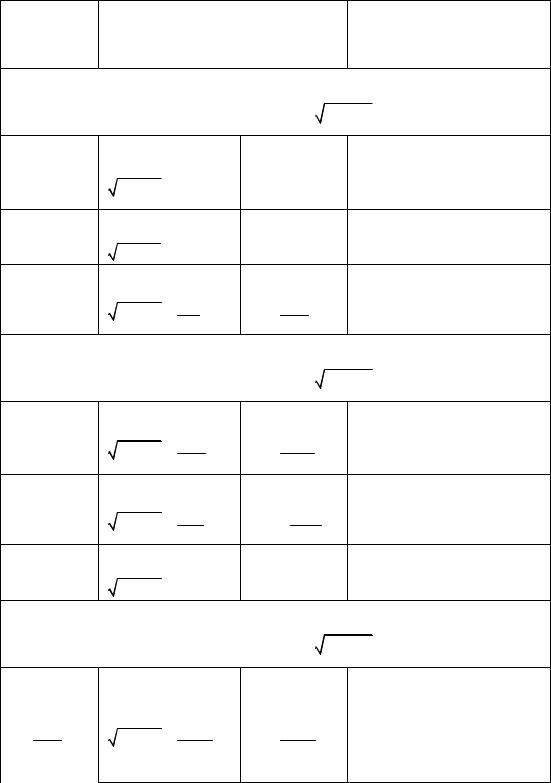
Интегралы такого вида легко приводятся к интегралам вида òR(sint,cost)dt или òR(sht,ch t)dt с помощью тригонометриче-
ских или, соответственно, гиперболических подстановок, приведен- ных в таблице. При этом особое внимание следует уделить области допустимых значений переменных (см. пример 8.38).
227
Подста- |
|
|
Элементы интеграла |
|
|
|
|
Область допустимых |
||||||||||||||
|
новка |
|
|
|
|
|
|
значений переменных |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Интегралы вида ò R(x, |
|
a2 − x2 )dx |
|
|
|
|
|
|
|
|||||||||
x = asin t |
a2 - x2 |
= acost |
dx = a cost dt |
é |
p |
, |
pù |
|
||||||||||||||
x Î[-a,a], t Î ê- |
2 |
2 |
ú |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
û |
|
|||
x = −acost |
a2 - x2 |
= asint |
dx = asint dt |
x Î[-a,a], t Î[0,p] |
|
|
|
|
||||||||||||||
x = a tht |
a2 - x2 |
= |
a |
dx = |
|
a2 |
t |
dt |
|
x Î[-a,a], t Î(-¥,¥) |
|
|||||||||||
|
|
|
|
|
|
|
cht |
|
ch |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Интегралы вида ò R(x, |
|
a2 + x2 )dx |
|
|
|
|
|
|
|
|||||||||
x = a tgt |
a |
2 |
+ x |
2 |
= |
a |
dx = |
adt |
|
|
|
æ |
|
|
p |
, |
p |
ö |
||||
|
|
cost |
cos |
2 |
t |
|
|
x Î(-¥,¥), t Îç - |
|
2 |
2 |
÷ |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
ø |
|||||||
x = a ctgt |
a2 + x2 |
= |
a |
dx = - |
adt |
|
|
x Î(-¥,¥), t Î(0,p) |
|
|
||||||||||||
|
|
|
|
|
|
|
sint |
|
|
sin2 t |
|
|
|
|
|
|
|
|
|
|||
x = asht |
a2 + x2 |
= a cht |
dx = ach t dt |
|
x Î(-¥,¥), t Î(-¥,¥) |
|
||||||||||||||||
|
|
|
|
Интегралы вида òR(x, |
|
x2 − a2 )dx |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
|
p |
ö |
|
или |
||
|
a |
|
|
|
|
|
asint |
|
asint |
|
|
x Î[a,+¥), t Î ê0, |
2 |
÷ |
|
|||||||
x = |
x |
2 |
- a |
2 |
= |
dx = |
dt |
ë |
|
ø |
|
|
||||||||||
cost |
|
|
cost |
cos2 t |
æ p |
|
|
ù |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x Î(-¥,-a], t Îç |
2 |
,pú |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
û |
|
|||
|
|
|
|
|
|
|
|
|
228 |
|
|
|
|
|
|
|
|
|
|
|||
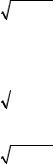
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
p |
ö |
или |
|
a |
|
|
|
|
|
|
|
acost |
|
|
acost dt |
|
x Î[a,+¥), t Î ê- |
2 |
,0÷ |
|
|
|
|
|
|
|
|
|
|
|
ë |
ø |
|
|||||
x = - |
x |
2 |
- a |
2 |
= |
|
dx = |
|
|||||||||
sin t |
|
|
|
sint |
|
sin2 t |
|
æ |
0, |
pù |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x Î(-¥,-a], t Îç |
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
2 û |
|
x = a ch t |
|
|
|
|
|
= ash t |
|
dx = asht dt |
|
x Î[a,+¥), t Î[0,+¥) |
|
||||||
x2 - a2 |
|
||||||||||||||||
x = −a ch t |
|
|
|
|
|
= -asht |
|
dx = −asht dt |
|
x Î(-¥,-a], t Î(-¥,0] |
|
||||||
x2 - a2 |
|
||||||||||||||||
Зам е ч ан и е 1 . a > 0.
Зам е ч ан и е 2 . Выбор конкретной подстановки зависит от вы-
числяемого интеграла.
229
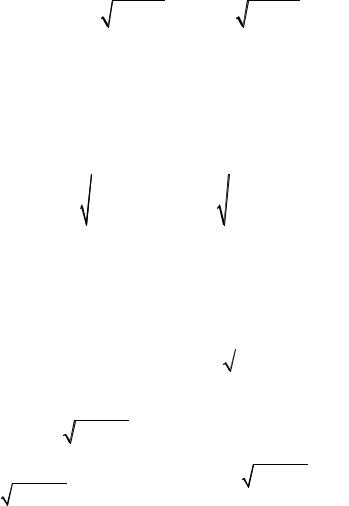
Пр и ме р 8.37. Вычислим интеграл ò |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
, a > 0. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
(a2 + x2 )2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4Подстановка x = a tgt : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
|
+ x |
2 |
= |
|
|
|
a2 |
, |
|
|
|
dx = |
|
|
adt |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 t |
|
|
|
cos2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
I = ò |
|
|
|
|
|
|
dx |
|
|
|
|
|
= ò |
|
cos4 t |
|
|
|
|
adt |
|
|
|
= |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
(a2 |
+ x2 ) |
2 |
|
|
|
a |
4 |
|
|
|
cos |
2 |
t |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
= |
|
1 |
ò |
1+ cos2t dt = |
|
|
|
t |
|
+ sin 23 t |
|
+ C . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
4a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Учитывая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
tgt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
sint = |
|
|
|
|
|
|
|
|
, cost = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
1+ tg2t |
|
|
|
1+ tg2t |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I = |
1 |
|
(t + sint cost) + C = |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2a3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
æ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
|
|
|
|
|
|
|
|
|
|
x ù |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|||||
|
1 |
|
ç |
|
x |
|
|
|
|
|
|
|
|
|
tg |
êarctg |
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
÷ |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
= |
|
çarctg |
|
+ |
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
a û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
+ C = |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2a |
3 |
ç |
|
a |
|
|
|
|
|
|
|
1+ tg2 |
éarctg |
x |
ù |
|
|
|
|
|
|
+ tg2 |
éarctg |
x |
ù |
÷ |
|
||||||||||||||||||||||||||||||||||||||||
|
|
ç |
|
|
|
|
|
|
|
|
|
|
|
1 |
÷ |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
ú ÷ |
|
||||||||||
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
a û |
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
a û |
ø |
|
|||||||||||||
|
|
|
|
|
= |
|
1 |
|
|
arctg |
x |
|
+ |
|
|
1 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
+ C .3 |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2a3 |
|
|
|
2a2 a2 + x2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Пр и ме р 8.38. Вычислим интеграл ò |
|
|
|
|
|
dx |
|
|
|
|
, x > a > 0 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x |
2 |
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4Так как x > a , то для вычисления данного интеграла использу- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ем подстановку x = ach t : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 - a2 |
= ash t, |
|
|
dx = ashtdt , |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
ò |
|
|
dx |
|
|
|
|
|
|
òdt = t + C = ln (x + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)+ C .3 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
x |
2 |
|
- a |
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x2 - a2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
230
Пр и ме р 8.39. Вычислим интеграл ò |
|
x2 |
- a2 dx |
, a |
> 0. |
|||||||||||||||||||||||||
|
|
|
|
x |
4 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||
4Используем подстановку x = |
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
cost |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
= asint |
|
|
dx = asin t dt , |
|
|
|||||||||||||||||
|
|
|
|
x2 - a2 |
, |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
cost |
|
|
|
|
|
|
|
|
|
cos2 t |
|
|
|
|
|
||||||
ò |
|
|
x2 |
- a2 dx |
|
= ò |
asin t |
× |
cos4 t |
× |
|
asin t |
dt = |
|
||||||||||||||||
|
|
|
x |
4 |
|
|
cost |
|
a |
4 |
|
|
cos |
2 |
t |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
|
sin3 t + C = |
1 |
|
|
|
æ |
|
- a |
2 ö3/ 2 |
|
|
|
|
|
|||||||||||||
= |
|
|
|
ç1 |
|
÷ |
|
|
+ C .3 |
|
||||||||||||||||||||
3a |
2 |
3a |
2 |
|
2 |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
x |
|
ø |
|
|
|
|
|
|
|
|
|||
8.9.ОБЩИЕ ЗАМЕЧАНИЯ ОБ ИНТЕГРИРОВАНИИ. НЕБЕРУЩИЕСЯ ИНТЕГРАЛЫ
Вдифференциальном исчислении было показано, что дифферен- цирование элементарных функций есть всегда выполнимое (в элемен- тарных же функциях) действие. Для интегрирования подобное утвер-
ждение неверно. В частности, доказано, что интегралы от некоторых элементарных функций уже не являются элементарными функциями. Приведем для примера некоторые из них:
|
|
|
x |
|
|
dx |
|
|
|
|
|
|
|
|
òe− x2 dx , ò |
e |
dx , ò |
, |
òcos x2dx, òsin x2dx , |
||||||||||
n |
ln x |
|||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
||
ò |
cos x |
dx , |
ò |
sin x |
dx , |
ò |
sh x |
dx, |
ò |
ch x |
dx. |
|||
n |
n |
n |
n |
|||||||||||
|
x |
|
x |
|
|
|
|
x |
|
x |
||||
Каждый из указанных интегралов представляет собой функцию, не являющуюся элементарной. Данные интегралы не только реаль- но существуют, но и играют большую роль в различных вопросах физики.
231
