Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Глава 8

.pdf

Скачиваний:

Добавлен:

11.03.2016

Размер:

540.54 Кб

Скачать

☆

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Пр и ме р 8.10. Разложим дробь

x2 + 5x +1

на сумму

(

x2 +1

x2 + 4

)(

2 + 9

)

простейших дробей.

)(

4Разложение данной дроби имеет вид

x2 + 5x +1

Ax + B

Cx + D

Ex + F

x2 +1 +

x2 + 4

x2 + 9

(x2 +1)(x2 + 4)(x2 + 9)

следовательно,

(

x2 + 5x +1 = ( Ax + B)(x2 + 4)(x2 + 9)+

)

Cx + D

)(

+ 9

)

(

Ex + F

)(

(8.8)

x2 +1 x2

x2 +1 x2 + 4

Найдем коэффициенты методом частных значений. Положив в равенстве (8.8) поочередно x = i, x = 2i, x = 3i и приравняв действи-

тельные и мнимые части, получим:

1)5i = 24Ai + 24B , то есть A = 5/ 24, B = 0 ;

2)10i - 3 = -15C × 2i -15D , то есть C = −1/3, D = 1/5;

3)15i -8 = 40E ×3i + 40F , то есть E = 1/8, F = −1/5.3

Пр и ме р 8.11. Разложим дробь		2x3 + 4x2 + x + 2						на сумму про-
	(	)	2	(	x2		)

		x −1				+ x +1

стейших правильных дробей.

4Убедившись в том, что квадратный трехчлен x2 + x +1 имеет комплексные корни, ищем разложение дроби в виде

		2x3 + 4x2 + x + 2								=			A		+		B			+	Cx + D			.		(8.9)
(		)		(					)	=					+	(		)		+				.		(8.9)
(		)	2	(					)			x −1				(		)	2		x	2	+ x +1
		x −1			x	2	+ x	+1				x −1					x −1				x		+ x +1
						2

Способ 1. Используем метод сравнения.
Приводя равенство (8.9) к общему знаменателю, получим
								2x3 + 4x2 + x + 2										=
							(			)	(						)	=
							(			)	(						)
								x −1 2					x2 + x +1
=	A(x −1)(x2 + x +1)+ B(x2 + x +1)+ (Cx + D)(x −1)2																								.
=																									.
								(			)		(	x2				)
									x −1 2					x2	+ x +1

Приравнивая коэффициенты при одинаковых степенях, прихо-

дим к системе уравнений

194

2 = A +C;

4 = B + D − 2C;

1 = B + C − 2D;

2 =−A+ B + D.

Решая эту систему, находим

A = 2 ,

B = 3,

C = 0 ,

D = 1. Таким

образом, окончательно получаем

2x3 + 4x2 + x + 2

(

) (

)

(

)

x −1

+ x +1

x −1

+ x +1

x −1

Способ 2. Решим этот же пример, используя метод частных значений. Перепишем выражение (8.9) в виде

2x3 + 4x2 + x + 2 =

=A(x −1)(x2 + x +1)+ B(x2 + x +1)+ (Cx + D)(x −1)2 . (8.10)

1)Полагая в (8.10) x = 1, получаем B = 3.

2)Чтобы найти коэффициент A, продифференцируем обе части выражения (8.10) и затем положим в нем x = 1. При дифференциро- вании правой части будем выписывать только те слагаемые, кото-

рые не обращаются в нуль при x = 1:

6x2 + 8x +1 = A(x2 + x +1)+ B(2x2 +1)+ ....

Отсюда при x = 1 имеем 15 = 3A + 3B , то есть A = (15 − 3B)/3 = 2.

3)	Полагая в (8.10) x = 0, получим
	2 = −A + B + D Þ D = 2 + A − B = 1.
4)	Сравнивая коэффициенты при x3 , получим
	2 = A + C Þ C = 0.3

8.3.2. Интегрирование рациональной дроби

Теорема 8.5. Всякая рациональная дробь интегрируется в эле- ментарных функциях.

4Как уже отмечалось, интегрирование рациональной дроби сводится к интегрированию многочлена и правильной рациональ- ной дроби. Поэтому достаточно показать, что правильная рацио- нальная дробь интегрируется в элементарных функциях.

В силу теоремы 8.5, интегрирование правильной рациональной

дроби сводится к интегрированию простейших дробей следующих четырех типов:

195

1.	A	.	2.			A		, (k ³ 2). 3.	Mx + N	.
	x - b			(x - b)k					x2 + px + q

4.	Mx + N					, (m	³ 2).
	(x2 + px + q)m
Здесь A, M , N, b,					p, q – некоторые вещественные числа, причем
трехчлен	x2 + px + q					не имеет действительных корней, то есть

q - p2 > 0 . Докажем, что каждая из четырех указанных дробей ин- 4

тегрируется в элементарных функциях. 1. ò xAdx- b = Aln x - b + C .

2. ò	Adx	= [t = x - b] = Aò dtk		= -	A		+ C =
2. ò	k	= [t = x - b] = Aò dtk		= -	(k -1)t	k −1	+ C =
	(x - b)		t		(k -1)t
		= -	A	+ C.
		= -	(k -1)(x - b)k −1	+ C.

3. Для вычисления интеграла типа 3 представим квадратный

трехчлен в виде

(	2 )	2	è	4	ø
x2 + px + q = x + p			+ ç q - p		÷

и, учитывая, a = 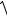q − p2 4

что q - p2		> 0, введем в рассмотрение постоянную
4
. Тогда, сделав подстановку t = x + p					, получим
			Mt + (N - Mp / 2)	2
ò	Mx + N	dx = ò		dt	=
	x2 + px + q		t2 + a2

=M ò d (t2 + a2 ) + (N 2 t2 + a2

=M ln (t2 + a2 )+ æç 2N

2 è

-Mp

/ 2)ò			dt			=
/ 2)ò	t	2	+ a		2	=
	t		+ a
ö			t	+ C =
÷arctg
÷arctg			a
ø			a

x + p

2N - Mp

ln(x2

+ px + q)+ ç

÷arctgç

q - p

÷ + C.

196

4. Используя введенные выше обозначения, получим

Mx + N

Mt +

ç N

= ò

dt =

(x2 + px + q)m

(t2 + a2 )m

M d (t2 + a2 )

Mp ö

ç N -

ò (t2 + a2 )

(t2 + a2 )

øò

Mp ö

+ ç N -

÷ Im .

(

)(

)

m−1

2 1- m

+ px + q

Рассмотрим интеграл

Im = ò

Если представить

Im в

(t2 + a2 )m

виде линейной комбинации интегралов Im−1 и ò

t2dt

и вычис-

(t2 + a2 )m

лить последний интегрированием по частям, получим

Im = ò

(t2 + a2 )- t

òt

tdt

(t2 + a2 )m

dt =

Im−1 -

(t2 + a2 )m

Im−1 -

òtd ç

2(1- m)(t

+ a

)

m−1

Im−1 +

2a2 (m -1)(t2 + a2 )m−1

2(m -1)a2

(t2 + a2 )m−1

2m - 3

Im−1.

2a2 (m -1)(t2 + a2 )m−1

2a2 (m -1)

Таким образом, мы получили рекуррентную формулу для вы- числения интеграла Im при m > 1. Если m = 1, то

			dt		1		t	%
Im = I1	=			=		arctg		+ C .
Im = I1	=	òt2	+ a2	=	a	arctg	a	+ C .
		òt2	+ a2		a		a

Таким образом, нами вычислены интегралы от всех четырех ти- пов простейших дробей и доказано, что каждый из этих интегралов

представляет собой элементарную функцию.3

197

Пр и ме р 8.12. Вычислим интеграл от дроби из примера 8.11.

4ò

2x3

+ 4x2 + x + 2

dx = ò

dx + ò

(

)

(

)

(

)

x -1

+ x +1

x -

1 x + x +1

x -1

d ç x +

= 2ln

x -1

+ ò

x -1

1 ö2

ç x +

2 ø

= 2ln

x -1

arctg

+ C.3

x -1

З ам е ч ан и е . Указанный в теореме метод вычисления неопреде- ленного интеграла от рациональной дроби позволяет вычислить ин- теграл от любой рациональной дроби, если можно получить кон- кретное разложение знаменателя на множители вида (8.6). Но в от-

дельных частных случаях бывает целесообразнее для значительного сокращения вычислений действовать иными путями.

Пр и ме р 8.13. Вычислим интеграл ò																																									x5			+ 3x3 + 2x															dx .
Пр и ме р 8.13. Вычислим интеграл ò																																											(	x2 +1 10															dx .
																																											(										)
4Разделив числитель на x2 +1 с остатком, получим
					x + 3x + 2x																									(											)						(									)
						5						3																	x			x		2		+1 + x														x		2	+1				2
			ò																		dx = ò													2																		2
																																																											dx =

							(		x2		+1				10																						(		x2 +1									10
							(							)																							(										)
											= ò											x					dx + ò															x							dx =
											= ò				(				2						9		dx + ò								(					2						8			dx =
															(			x						)											(			x						)
																		x				+1																x					+1
1			dx2								1								dx2														1										1										1					1
= 2 ò										+			ò													= -																								-											+ C.3
= 2 ò		(	x2 +1					9		+	2		ò		(		x2 +1								8	= -					16					(		x2					+1				8			-			14			(	x2 +1			7	+ C.3
		(				)									(								)													(										)										(		)
Пр и ме р 8.14. Вычислим интеграл ò																																													dx									.
Пр и ме р 8.14. Вычислим интеграл ò																																									x(x5 + 2)													.
4ò			dx						=		1	ò								dx5								=
4ò	x(x5 + 2)								=		5	ò		x5 (x5 + 2)														=
								1			æ 1											1					ö				5							1										x5
								1			æ 1											1					ö				5							1										x5
				=							ç					-											÷dx							=									ln												+ C.3
				=		10 ò					ç			5		-				x		5	+ 2				÷dx							=		10							ln			x		5			+		2		+ C.3
						10 ò					è x									x			+ 2				ø									10										x					+		2

198

ù¢

8.3.3. Метод Остроградского

P(x)

Если знаменатель правильной рациональной дроби Q(x) имеет

кратные корни, особенно комплексные, то интегрирование такой дроби обычно связано с громоздкими выкладками. В этом случае целесообразно использовать метод Остроградского, суть которого состоит в выделении рациональной части первообразной.

Пусть Q(x) имеет кратные корни (включая и комплексные). Со- ставим многочлен Q2 (x) так, чтобы все его корни были простые и

каждый корень Q(x) был корнем Q2 (x). Тогда Q(x) = Q1 (x)Q2 (x), где корни Q1 (x) есть корни многочлена Q с кратностями каждый на единицу меньше, то есть

Q(x) = (x − b1 )k1 L(x − bm )km (x2 + p1x + q1 )l1 L(x2 + pn x + qn )ln ; Q1(x) = (x − b1 )k1−1L(x − bm )km −1 (x2 + p1x + q1 )l1 −1L(x2 + pn x + qn )ln −1 ;

Q2 (x) = (x - b1 )L(x - bm )(x2 + p1x + q1 )L(x2 + pn x + qn ).
Тогда справедливо соотношение
ò	P(x)	dx =	R(x)	+ ò	S (x)	dx,	(8.11)
			Q1 (x)		Q2 (x)
	Q(x)

где R(x) и S (x) – многочлены с неопределенными коэффициентами, степени которых соответственно на единицу меньше степеней много- членов Q1 (x) и Q2 (x). Для отыскания коэффициентов многочленов R(x) и S (x) необходимо продифференцировать равенство (8.11),

привести результат дифференцирования к общему знаменателю и со- поставить коэффициенты при одинаковых степенях x в числителе.

З ам е ч ан и е . В формуле	P(x)	é	R	(x) ù¢			S (x)	, полученной
		= ê			ú	+
	Q(x)						Q2 (x)
		ëQ1		(x)û

é R(x)

дифференцированием формулы (8.11), дробь êëQ1 (x) после надле-

жащих сокращений приводится к знаменателю Q(x).

199

Пр и ме р 8.15. Вычислим методом Остроградского интеграл

I = ò

x6 − x5 + x4 + 3x2 − 2x + 2

dx .

(

x −1

(

)

4Используя введенные выше обозначения, получим

)

(

)

(

)

(

)

(

2 ;

= x6 − x5 + x4

+ 3x2 − 2x

+ 2, Q

−1 3

Q1 (x) = (x −1)2 (x2 +1), Q2 (x) = (x −1)(x2 +1).

Тогда

P(x)

dx = Ax3 + Bx2 + Cx + D + òTx2 + Sx +U dx =

Q(x)

Q1 (x)

Q2 (x)

Ax3

+ Bx2

+ Cx + D

dx +

Fx + H

dx.

Q1 (x)

−1

Продифференцировав это равенство и приведя его правую часть к общему знаменателю, приравняем коэффициенты при одинаковых

степенях x у многочленов, стоящих в числителях:

= E + F;

−1 = − 3F − A + H − 2E;

1 = − A + 4F − 2B + 3E − 3H;

0 = A − 4E + 4H − 3C − 4F;

3 = − 3A − 4D + C + 3E + 3F − 4H;

−2 = − F − 2B − C − 2E + 2D + 3H;

2 = − H − C − 2D + E.

Решив эту систему уравнений, находим

A = − 3

, B = 1, C = − 5 , D = 0, E = 1, F = 0, H =

1 .

Таким образом,

P(x)

−3x3 + 4x2 − 5x

dx 1 dx

4Q1 (x)

+ ò

Q(x)

x −1

x2 +1

−3x3 + 4x2 − 5x

+ ln

x −1

arctg x + C.3

(

)

− 2x3 + 2x2 − 2x +1

200

Многочлен Q1 (x) может быть найден без разложения как наи- больший общий делитель многочленов Q( x) и Q′(x) с использова- нием алгоритма Евклида.

Алгоритм Евклида

Пусть необходимо найти наибольший общий делитель много- членов f (x) и ϕ(x). Не ограничивая общности, будем считать, что

степень ϕ( x) не выше степени f (x).

Многочлен f (x) представим в виде:
f (x) = ϕ(x)q(x) + r1 (x),	(1)

где r1 (x) – остаток от деления f (x) на ϕ( x) . Тогда степень r1 (x) меньше степени делителя ϕ(x).

Далее, в результате деления ϕ(x) на r1 (x) получим:
ϕ(x) = r1 (x)q1 (x) + r2 (x) ,	(2)
причем степень r2 (x) меньше степени делителя r1(x) .
r1 (x) = r2 (x)q2 (x) + r3 (x)	(3)
...
rk −2 (x) = rk −1 (x)qk −1 (x) + rk (x)	(k )

При каждом делении степень остатка будет снижаться по край- ней мере на единицу, поэтому на определенном шаге мы получим

нулевой остаток, то есть
rk −1 (x) = rk (x)qk (x).	(k +1)

Последний отличный от нуля остаток rk (x) является наиболь- шим общим делителем многочленов f (x) и ϕ(x).

4Достаточно доказать два утверждения:

1)многочлены f (x) и ϕ( x) делятся на rk (x) , то есть rk (x) – один из делителей f (x) и ϕ(x);

2)многочлен rk (x) делится на любой делитель r0 (x) многочле-

нов f (x) и ϕ( x), то есть rk (x) – наибольший общий делитель ука-

занных многочленов.

Для доказательства утверждения 1 заметим, что, в силу (k +1), rk −1 (x) делится на rk (x), а тогда, в силу (k ), rk −2 (x) делится на

201

rk (x). Поднимаясь вверх по цепочке равенств (1) – (k ), мы докажем,

что f (x) и ϕ(x) делятся на rk (x) .

Докажем утверждение 2. Пусть r0 (x) – произвольный делитель многочленов f (x) и ϕ(x). В силу равенства (1) r1 (x) делится на r0 (x) , а тогда, в силу равенства (2), r2 (x) делится на r0 (x) . Опускаясь по цепочке равенств (1) – (k ), докажем, что rk (x) делится на r0 (x).3

	Пр и ме р 8.16. Вычислим интеграл
													ò								x6 − x5 + x4 + 3x2 − 2x + 2
																																						dx .
																	x7 − 3x6 + 5x5 − 7x4 + 7x3 − 5x2 + 3x −1																					dx .
	4Используем метод Остроградского. Для нахождения много-
члена					Q1 (x) = НОД (Q(x),Q′(x)) воспользуемся алгоритмом Евк-
лида. Тогда
												Q(x) = x7 − 3x6 + 5x5 − 7x4 + 7x3 − 5x2 + 3x −1,
											Q′(x) = 7x6 −18x5 + 25x4 − 28x3 + 21x2 −10x + 3.
	Согласно алгоритму,																						представим Q(x) в виде
																					Q(x) = Q′(x)q(x) + r1 (x).
−	x7 − 3x6 + 5x5 − 7x4 + 7x3 − 5x2 + 3x −1																																		7x6 −18x5 + 25x4 − 28x3 + 21x2 −10x + 3
	x7 − 3x6 + 5x5 − 7x4 + 7x3 − 5x2 + 3x −1																																		7x6 −18x5 + 25x4 − 28x3 + 21x2 −10x + 3
	7		18						6		25							5		4		3	10					2		3						1			3
	x	−					x			+					x				− 4x		+ 3x		−			x			+				x				7 x −
				7									7											7							7
				7									7											7							7								49
																																							49
				−		3		x6 +						10		x5				− 3x	4 + 4x3 −				25		x2 +					18		x −1
	− −			−		7		x6 +					7			x5				− 3x	4 + 4x3 −			7			x2 +					7		x −1
						7							7											7								7
			3		x6				+		54 x5 −									75 x	4 +	12 x3 −				9 x2				+			30 x−			9
			7		x6				+		54 x5 −									75 x	4 +	12 x3 −				9 x2				+			30 x−			49
			7								49									49		7				7						49				49
											16 x5							−		72 x4 +		16 x3 −				16 x2 + 96 x − 40 = r1 (x).
											49									49		7				7						49				49

Так как наибольший общий делитель многочленов определен с точностью до произвольного постоянного множителя, то вместо

многочлена r1 (x) будем рассматривать многочлен

r%1 (x) = 494 r1 (x) = 4x5 −18x4 + 28x3 − 28x2 + 24x −10 .

202

−

7x6 −18x5 + 25x4 − 28x3 + 21x2 −10x + 3

4x5 −18x4 + 28x3 − 28x2 + 24x −10

−

+ 49x

− 49x

+ 42x

− 2 x

x +

27 x5 − 24x4

+ 21x3 − 21x2 +

15 x + 3

−

27 x5 −

243 x4

189 x3 −

189 x2

+ 81x − 135

147

−

147

−

147

x +

147

= r2 (x).

Аналогично предыдущему шагу сделаем замену

r%2 (x) =

4r2 (x)

= x4 − 2x3

+ 2x2 − 2x +1.

147

x4 − 2x3 + 2x2 − 2x +1

−

4x5 −18x4 + 28x3 − 28x2 + 24x −10

4x5 −8x

4 + 8x3 − 8x2 + 4x

4x −10

−−10x4 + 20x3 − 20x2 + 20x −10 −10x4 + 20x3 − 20x2 + 20x −10

0 = r3 (x).

Таким образом,
ò	x5 + x −1	dx =	Ax3 + Bx2 + Cx + D	+ ò Ex2 + Fx + H dx,
			Q1 (x)
	Q(x)					Q2 (x)
где Q1 (x) = x4 − 2x3 + 2x2 − 2x +1, Q2 (x) =					Q(x)	= x3 − x2 + x −1.
					Q1 (x)

Продифференцировав это равенство и приведя его правую часть к общему знаменателю, приравняем коэффициенты при одинаковых степенях x у многочленов, стоящих в числителях:

x6	1	=	E;

x5	−1 =		F − 2E − A;
x4	1 =		H − A + 2(E − B − F );
x3	0 = A − 2(E − F + H ) − 3C;
x2	3 = 2H − 4D − 3A + C + E − 2F;
x1	−2 =		F + 2D − C − 2B − 2H;
x0	2 = − 2D − C + H.
			203

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.03.2016546.03 Кб8Глава 3,4.pdf
#
11.03.2016719.99 Кб7Глава 3.2.pdf
#
11.03.2016746.33 Кб8Глава 3.pdf
#
11.03.2016911.85 Кб7Глава 5.pdf
#
11.03.2016660.06 Кб5Глава 6.pdf
#
11.03.2016540.54 Кб7Глава 8.pdf
#
23.09.2019497.15 Кб8Главная Шпора ТФКП теория.doc
#
27.03.20151.92 Mб123Голуб курсач.doc
#
27.03.20151.69 Mб20Горин С.А. - НЛП. Техники россыпью [2004].doc
#
22.09.2019694.27 Кб8ГОСЫ КПРФ.doc
#
21.09.2019310.78 Кб1Госы ответы ФиК.doc