
Глава 8
.pdf
Интегралы I-го типа. Можно показать, что первообразная для
функции |
|
|
|
|
P(x) |
|
|
имеет вид |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
ax2 + bx + c |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
P(x) |
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
ò |
|
|
|
|
|
dx = Q(x) ax |
2 |
+ bx + c + lò |
|
|
|
|
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
ax |
2 |
+ bx + c |
|
ax |
2 |
+ bx + c |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где Q(x) |
|
– многочлен степени (n −1) |
с неопределенными коэффи- |
|||||||||||||||||
циентами, λ |
– неизвестная константа. |
Коэффициенты многочлена |
||||||||||||||||||
Q(x) и число λ находятся при помощи дифференцирования по-
следнего равенства. |
|
|
Adx |
|
|
|
||
Интегралы II-го типа. Интеграл ò |
|
|
|
|
подста- |
|||
|
k |
|
|
|
|
|
||
(x - g) |
|
ax |
2 |
|
||||
|
|
|
|
+ bx + c |
||||
новкой (x − γ) = 1t приводится к интегралу типа I.
Интегралы III-го типа. Для данного типа интегралов рассмот- рим два случая.
1. Предположим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ax2 + bx + c = a(x2 + px + q). |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
M |
(2x + p) + N |
|
|
|
Mp ö |
||||||||||||
|
|
|
|
|
|
(Mx + N )dx |
|
|
|
|
|
|
|
|
|
ç |
|
|
|
- |
|
|
|
|
|
|
÷dx |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
è |
|
|
|
|
|
|
|
ø |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||
ò(x2 + px + q) |
|
ax2 |
+ bx + c ò |
|
|
|
|
|
|
|
|
|
|
(x2 + px + q)m+ |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
= C |
|
|
|
d (x2 + px + q) |
|
+ B |
|
|
|
|
|
|
|
|
dx |
|
|
= |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
ò (x2 + px + q)m+ |
1 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
ò(x2 + px + q)m+ 2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
= C |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
+ B |
|
|
|
dx |
|
|
|
|
|
|
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||
|
|
|
|
|
|
|
(1- 2m)(x2 + px + q)m− |
|
|
|
|
|
|
|
ò (x2 + px + q)m+ |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||
|
|
1 |
æ |
|
|
Mp ö |
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где B = |
|
|
|
|
ç N - |
|
|
|
|
÷, C |
= |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
a è |
ø |
|
2 |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(8.18)
=
Прежде чем продолжить ход рассуждений, рассмотрим теорему.
214
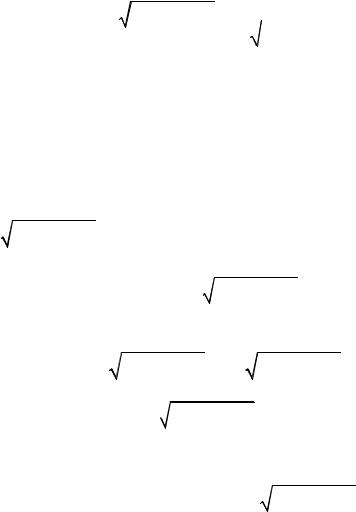
Теорема 8.9. Интегралы вида |
|
|
|
|
|
dx |
|
, где многочлен |
|||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
||||||||||||||||||||||||||||||||||
x2 + px + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ò(x2 + px + q)m+ 2 |
|
|
|
|
|||||||||||
|
не имеет действительных корней, рационализируются |
||||||||||||||||||||||||||||||||||||||
подстановкой Абеля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
t = ( |
|
|
|
|
|
|
|
|
|
|
)¢ = |
|
|
|
x + p / 2 |
|
. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
x2 + px + q |
|
|
|
(8.19) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + px + q |
|
|
|
|
||||
41°. (x |
2 |
+ px + q) = |
|
p2 / 4 - q |
= R(t), так как из (8.19) следует, |
||||||||||||||||||||||||||||||||||
|
|
|
t2 -1 |
|
|
|
|||||||||||||||||||||||||||||||||
что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
2 |
|
|
|
|
|
æ |
p |
2 |
ö |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
t2 (x2 + px + q) |
= çæ x + |
|
÷ö |
|
|
|
= (x2 |
|
+ px + q)+ ç |
|
- q ÷. |
||||||||||||||||||||||||||
2 |
|
|
|
|
4 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
ø |
|
|
|
|
|
|
|
è |
ø |
||||||||||||
2°. |
|
|
|
dx |
|
|
= |
|
dt |
|
. Действительно, если продифференциро- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1- t2 |
||||||||||||||||||||||||||||||||
|
|
x2 |
+ px + q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
вать (отдельно левую и правую части) равенство |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x + |
|
= t x2 + px + q , |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
эквивалентное равенству (8.19), то получим |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
dx = dt × |
|
+ t ×( |
|
|
)' |
|
||||||||||||||||||||||||||||
|
|
|
|
|
x2 + px + q |
|
x2 + px + q |
dx = |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
= dt × 
 x2 + px + q + t ×t dx..
x2 + px + q + t ×t dx..
Из 1° и 2° следует, что |
|
|
|
|
|
|
|
|
||||||
|
dx |
|
= |
|
1 |
|
× |
|
dx |
|
= |
|
R(t)dt .3 |
|
ò |
(x2 + px + q)m+ |
1 |
ò (x2 + px + q) |
m |
|
|
|
ò |
||||||
x2 + px + q |
||||||||||||||
2 |
|
|
|
|
|
|
|
|||||||
2. Если равенство (8.18) не выполняется, то есть отношение трехчленов ax2 + bx + c и x2 + px + q непостоянно, то в интеграле
делают замену переменного так, чтобы во вновь полученных трех- членах одновременно исчезли члены с первой степенью. Это дости- гается, например, с помощью дробно-линейной подстановки
x = |
αt + β |
, если p ¹ b |
и x = t - |
p |
, если p = b . |
t +1 |
|
||||
|
a |
2 |
a |
||
215

At + B
В результате получаем интеграл ò(t2 + l)m st2 + r dt . Для вы-
числения этого интеграла представим его в виде
At + B
ò(t2 + l)m 
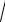 st2 + r dt =
st2 + r dt =
= Aò |
t dt |
|
+ B ò |
dt |
|
= A× I1 + B × I2. |
||
(t2 + l)m |
|
|
(t2 + l)m |
|
|
|||
st2 + r |
st2 + r |
|||||||
Покажем, что первый из этих интегралов рационализируется под-
становкой u = 
 st2 + r , а второй – подстановкой Абеля v = (
st2 + r , а второй – подстановкой Абеля v = (
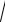 st2 + r )¢.
st2 + r )¢.
|
|
|
|
|
|
|
|
|
m |
æ |
|
2 |
- r |
öm |
|||
4Пусть u = st2 + r , тогда (t2 + l) |
|||||||||||||||||
|
= ç u |
|
+ l÷ |
= R(u), |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
è |
|
|
s |
ø |
|
||
|
du = |
|
|
stdt |
|
Þ |
|
|
tdt |
= |
du |
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
st2 + r |
|
|
|
st2 + r |
|
|
s |
|
|
||||
Для рационализации второго интеграла необходимо проделать
следующие выкладки: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
v = ( |
|
|
|
)¢ = |
|
|
|
st |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
st2 + r |
|
Þ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
st2 + r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
æ |
|
|
|
2 |
r |
|
|
|
|
ö |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Þ v2 (st2 + r) = s2t2 Þ (t |
2 + l) |
|
= ç |
|
|
|
v |
|
+ l÷ = R(v). |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
2 |
2 |
s |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è s |
- v |
|
|
|
ø |
|
|
|
|
|
|
||||||
st = v |
|
|
st2 + r Þ |
|
|
+ v ×( |
|
|
|
|
|
|
)' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Þ sdt = dv × st2 |
+ r |
st2 + r |
dt = dv × |
|
st2 + r + v2dt |
Þ |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
= |
|
dv |
|
.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s - v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
st2 + r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пр и ме р 8.26. Вычислим интеграл ò |
|
|
|
|
|
dx |
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
( |
|
|
|
|
|
|
5 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 - x +1 |
|
|
|
|
|
|
|
|
|
|||||
4Воспользуемся подстановкой Абеля: |
|
|
|
|
|
|
- x +1= |
4 1-t2 . |
||||||||||||||||||||||||||||||||||
1°. 4t |
2 |
(x |
- x +1)=4x |
-4x +1=4(x |
|
- x +1)-3 Þ x |
||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
) |
|
216
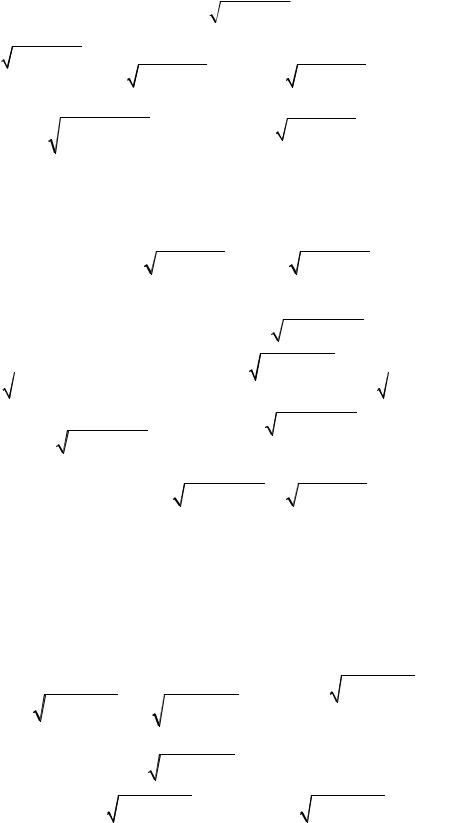
2°. Дифференцируя равенство t
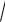 x2 - x +1 = x -1/ 2, получаем:
x2 - x +1 = x -1/ 2, получаем:
dt × |
|
|
|
|
+ t × |
(2x -1)dx |
|
= dx Þ |
|
|
|
|
|
dx |
|
|
|
|
dt |
|
|||||||||||||||||||||||||||||
x2 - x +1 |
|
|
|
|
|
|
= |
. |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1- t2 |
|||||||||||||||||||||||||||||||||
2 x2 - x +1 |
|
|
|
x2 - x + |
1 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
) |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
( |
|
|
|
|
) |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
2 |
|
- x +1 |
|
|
|
|
|
|
|
|
|
x |
|
|
- x +1 |
|
|
|
x - x +1 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ò |
|
16(1- t2 )2 |
× |
|
|
|
dt |
|
|
= |
16 ò(1- t2 )dt = |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
- t |
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
ö3 |
|
|
||||||||||||
|
16 |
æ |
|
t3 ö |
|
|
|
|
16 |
|
|
|
|
|
|
2x -1 |
|
|
|
|
|
16 |
æ |
|
|
|
|
|
2x -1 |
|
|
||||||||||||||||||
= |
|
|
çt - |
|
|
÷ + C = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
ç |
|
|
|
|
|
|
|
|
|
÷ |
+ C.3 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
9 |
3 |
|
|
9 2 x2 - x |
|
+1 |
|
27 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
è |
2 x2 - x +1 ø |
|
|
|||||||||||||||||||||||||||||||||
Пр и ме р 8.27. Вычислим интеграл ò |
x3 - 6x2 +11x - 6 |
dx . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
2 |
+ 4x + 3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x3-6x2+11x -6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
4ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx =(Ax |
+ Bx +C) |
|
x |
+4x +3 + lò |
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x2+ 4x +3 |
x2+4x +3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x3 - |
6x2 +11x - 6 |
= (2Ax + B) |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 + 4x + 3 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + 4x + 3 |
|
|
|
|
2x + 4 |
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
+(Ax |
2 |
+ Bx + C) |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 + 4x + 3 |
|
|
x2 + x +1 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
x3 - 6x2 +11x - 6 = (2Ax + B)(x2 + 4x + 3)+ (Ax2 + Bx + C)(x + 2) + l. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x3 |
|
|
1 |
|
= 2A |
|
|
|
|
|
|
+ A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A =1/3; |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
x2 |
|
|
-6 = 8A+ B + B + 2A |
|
|
|
|
|
|
|
|
|
|
B = -14/3; |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x1 |
|
|
11 = 6A+4B+C + 2B |
|
|
|
Þ C = 37; |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x0 |
|
|
-6 = |
|
|
+3B |
|
|
|
|
|
+2C +l |
|
|
|
|
|
l = -66. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Так как ò |
|
|
|
|
|
dx |
|
|
|
|
|
ò |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= ln |
x+2+ x2+4x +3 |
+C , то |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
+4x+3 |
|
|
|
|
|
|
(x +2) |
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ò |
x3-6x2+11x -6 |
dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2+ 4x +3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
æ |
x |
2 |
|
|
14x |
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
|
- |
+ |
|
|
|
x2+4x +3 - 66ln |
x + 2+ |
|
x2+ 4x +3 |
+C.3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
ç |
|
|
37÷ |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
è 3 |
|
|
3 |
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
217
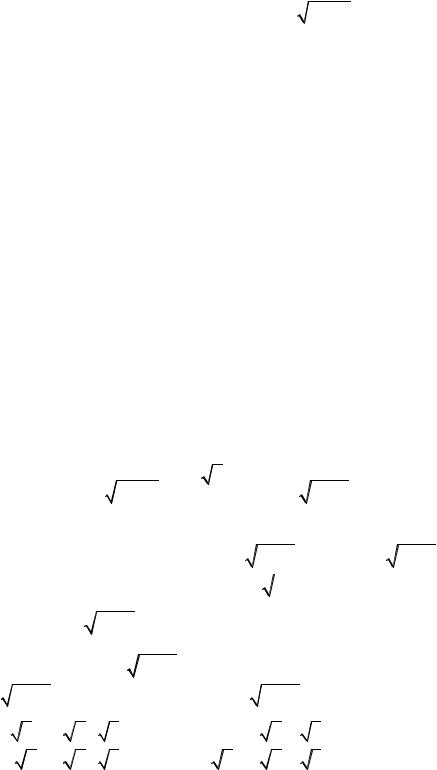
Пр и ме р 8.28. Вычислим интеграл ò |
|
|
|
2x + 5 |
|
|
|
dx . |
|
( |
x |
2 |
) |
|
|
|
|
||
|
2 |
+1 |
|||||||
|
|
|
+ x +1 x |
|
|
||||
4Так как отношение трехчленов x2 + x +1 и x2 +1 – не констан-
та, то делаем дробно-линейную подстановку x = |
αt + β |
. Тогда |
|
t +1 |
|
x2 + x +1 = a2t2 + 2abt +b2 + (at +b)(t +1) + t2 + 2t +1 ,
(t +1)2
x2 +1 = a2t2 + 2abt +b2 + t2 + 2t +1 . (t +1)2
Приравнивая к нулю коэффициент при t , получим систему для на- хождения α и β :
ì2ab + a + b + 2 = 0, íî2ab + 2 = 0.
Одно из решений этой системы: −α = β = −1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
В результате замены x = |
t −1 |
|
|
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
t +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x2 + x +1 = |
3t2 +1 |
, x2 +1 = |
2t2 + 2 |
, 2x + 5 = |
7t + 3 |
|
, dx = |
2 |
|
|
|
dt , |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(t +1)2 |
(t +1)2 |
|
t +1 |
(t +1)2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x + 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7t + 3 |
) |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
I = ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = 2ò |
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
2 |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
3t |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ x +1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t +1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Вычислим отдельно интегралы ò |
|
|
|
|
|
|
tdt |
|
|
|
|
|
|
|
|
|
|
, ò |
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
, |
||||||||||||||||||||||||||||||||||||||||||||||||
( |
|
2 |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
3t |
2 |
) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
+1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3t +1 t +1 |
|
|
|
|
|
|
|
|
|
|
+1 t |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
используя в первом из них подстановку u = |
|
|
|
|
|
t2 +1 , а во втором – |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
подстановку Абеля v = ( |
|
|
|
|
|
)′. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
t2 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
tdt |
|
|
|
|
|
|
|
é |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tdt |
ù |
|
|
|
|
|
|
|
|
|
|
du |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
u = |
|
|
t2 +1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
du = |
|
|
|
|
|
|
|
|
|
|
ú = ò |
|
|
= |
|
|
|
|||||||||||||||||||||||||
( |
|
|
|
) |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3u2 - 2 |
|
|
|
|||||||||||||||||||||||||||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
3t |
|
|
|
|
|
|
+1 |
|
ë |
|
|
|
+1 |
= 3u - 2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
+1 t |
|
|
|
|
|
ê3t |
|
|
|
|
|
|
|
|
|
|
|
t +1 ú |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
/ |
|
|
- u |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
- |
|
u |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
= |
× |
|
|
|
3 |
|
ln |
|
|
|
2 |
|
3 |
|
+ C = |
|
|
|
|
ln |
|
|
|
|
2 |
3 |
|
+ C. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
2 2 |
|
|
|
|
|
|
2 / 3 + u |
|
|
|
|
|
|
|
|
2 6 |
|
|
|
|
|
|
|
|
2 + 3u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
218

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
é |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
ù |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
|
|
|
v = |
|
( |
|
|
|
|
t2 + |
1 |
) |
= |
|
|
|
|
|
|
|
, |
|
|
|
ú |
|
||||||||||||||||||||||||
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 + |
1 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
= |
|||||||||||||||||||
(3t |
|
+1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
dv |
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2v |
2 |
|
|
ú |
|||||||||||||||||||||
2 |
|
|
t |
2 |
+ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ê |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
, 3t2 +1 = |
|
+1ú |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ê1 |
|
|
|
|
|
|
|
|
|
1+ t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1- v |
2 |
ú |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|||||||||
|
|
|
|
|
|
|
|
|
= ò |
|
|
|
|
|
dv |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
arctg |
|
|
|
|
|
2v |
+ C. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2v2 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tdt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
I = 7 2ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 3 2ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|||||||||||||||||||||||||||||||||
|
( |
3t |
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
( |
3t |
|
|
) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 t +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 t +1 |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
t2 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
= |
3 |
ln |
|
|
|
|
|
2 |
|
3 |
|
|
+ 3arctg |
|
|
|
|
|
2 |
|
|
+ C. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
t2 +1 |
|
|
|
|
|
|
t2 +1 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Учитывая, что t = |
x +1 |
, получаем окончательный ответ: |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(x -1) - |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
x2 + 2x + 2 |
|
|
+ |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
7 |
|
|
|
2 |
3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
I = |
3 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
(x -1)+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + 2x + 2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
(x +1)sgn (1- x) |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
+ C.3 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
+3arctgç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
|
|
2x |
2 |
+ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
8.5.ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
8.5.1. Интегралы вида òR(sinx,cosx)dx
Теорема 8.10. Интегралы вида òR(sin x,cos x) dx сводятся к ин-
тегралам от рациональной дроби при помощи подстановки t = tg |
x |
. |
|||||||||||||||||||||
|
|||||||||||||||||||||||
|
|
|
|
2t |
|
|
|
|
1- t2 , |
|
|
|
|
|
|
|
2dt |
2 |
|
||||
4Так как sin x = |
|
|
, |
cos x = |
x = 2arctgt , |
dx = |
, то |
||||||||||||||||
1 |
+ t2 |
|
|||||||||||||||||||||
|
|
|
æ |
|
1+ t2 |
|
ö |
|
|
|
|
|
1+ t2 |
|
|
|
|||||||
ò |
|
|
|
|
|
ò |
2t |
|
|
1- t |
2 |
|
2dt |
|
ò |
|
(t)dt .3 |
|
|
|
|||
R(sin x,cos x)dx = |
Rç |
|
, |
|
÷ |
|
= |
R1 |
|
|
|
||||||||||||
1+ t |
2 |
|
2 |
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
è |
|
1+ t |
|
ø |
1+ t |
|
|
|
|
|
|
|||||||
219
З ам е ч ан и е . Подстановка t = tg 2x , хотя и является универсаль-
ной подстановкой, часто приводит к довольно громоздким выклад- кам. В связи с этим укажем несколько частных случаев, когда по-
дынтегральная функция приводится к рациональной дроби более простым способом:
– если R(−sin x,cos x) = −R(sin x,cos x) , то применяется подстановка
t = cos x , sin x = |
|
, dx = - |
|
dt |
|
|
|
1- t2 |
|
; |
|||||
|
|
|
|||||
1- t2 |
|||||||
|
|
|
|
|
|||
– если R(sin x,−cos x) = −R(sin x,cos x) , то применяется подстановка
|
|
|
|
dt |
|
|
|
t = sin x , cos x = 1- t2 , dx = |
|
; |
|||||
|
|
|
|||||
1- t2 |
|||||||
|
|
|
|
|
|||
– если R(−sin x,−cos x) = R(sin x,cos x) , то применяется подстановка
t = tg x , sin x = |
|
|
t |
|
, cos x = |
1 |
|
, dx = |
|
|
dt |
. (8.20) |
|
|
|
|
|
|
|
|
1 |
+ t2 |
|||||
1 |
+ t2 |
|
|
1+ t2 |
|
|
|
||||||
Пр и ме р 8.29. Вычислим òsin3 xcos4 xdx.
4Так как R(−sin x,cos x) = (−sin x)3 (cos x)4 = −R(sin x,cos x), то
òsin3 xcos4 xdx = [t = cost] = -ò(1- t2 )t4dt = - t5 |
+ t7 |
+ C.3 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
7 |
|
|
Пр и ме р 8.30. Вычислим интеграл ò |
|
|
dx |
|
|
. |
|
|
|
||||||||||||||||||||
sin x |
+ cos x |
|
|
|
|||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4Полагая t = tg |
, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ò |
dx |
= ò |
|
|
|
|
1 |
|
|
|
|
× |
|
|
2dt |
= |
|
ò |
|
2dt |
|
= |
|||||||
sin x + cos x |
|
|
2t |
|
+ |
1- t2 |
|
1+ t2 |
|
|
-t2 + 2t +1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1+ t2 |
1+ t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2dt |
|
|
|
|
|
|
1 |
|
|
|
|
+ t -1 |
|
|
|
|
|
|
||||||
|
= ò |
|
|
|
|
|
= |
|
|
ln |
|
|
2 |
+ C .3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 - (t -1)2 |
|
|
|
|
|
|
- t +1 |
|
|
|||||||||||||||||||
|
|
|
|
2 |
|
2 |
|
|
|||||||||||||||||||||
220
Пр и ме р 8.31. Вычислим интеграл ò |
|
|
sin3 x dx |
|
. |
||||||||||||||||||
cos4 x (sin x + cos x) |
|||||||||||||||||||||||
4Пусть R(sin x,cos x) = |
|
|
|
sin3 x |
|
|
|
. Тогда |
|
|
|||||||||||||
cos4 x(sin x + cos x) |
|
|
|
||||||||||||||||||||
|
|
|
R(−sin x,−cos x) = R(sin x,cos x) , |
|
|
|
|
||||||||||||||||
поэтому применяем подстановку t = tg x: |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
ò |
|
sin3 x dx |
|
|
|
= ò |
sin3 x d (tg x) |
|
= |
|
|
|||||||||||
|
cos4 x (sin x + cos x) |
cos2 x (sin x + cos x) |
|
|
|||||||||||||||||||
|
|
tg3 x d(tg x) |
|
|
|
t3 dt |
|
æ |
|
2 |
|
|
|
1 |
|
ö |
|
|
|
||||
= |
|
|
|
|
|
= |
|
|
|
|
= |
çt |
|
- t +1 |
- |
|
|
÷ dt |
= |
|
|||
ò (1+ tg x) |
ò(t +1) |
|
t +1 |
|
|||||||||||||||||||
|
|
|
òè |
|
|
|
|
|
ø |
|
|
|
|||||||||||
|
= |
t3 |
- |
t2 |
+ t - ln | t +1| +C, t = tg x.3 |
|
|
|
|
||||||||||||||
|
3 |
2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8.5.2. Интегралы вида òsins x cosr xdx |
|
|
|
|
|
|
|
||||||||||||||||
Теорема 8.11. Пусть |
s,r ¤. Тогда интеграл |
òsins x cosr xdx |
|||||||||||||||||||||
с помощью подстановок u = sin x или u = cos x сводится к интегралу от дифференциального бинома.
4Для подстановки u = sin x получим:
1 |
|
|
|
|
|
du |
|
|
1 |
||
cos x = (1- u2 )2 |
, du = cos xdx Þ dx = |
= (1- u2 )− 2 du ; |
|||||||||
cos x |
|||||||||||
следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
1 |
|
|
|
r−1 |
||||
òsins x cosr xdx = òus (1- u2 ) |
|
(1- u2 )− |
|
du = òus (1- u2 ) |
|
|
du .3 |
||||
2 |
2 |
2 |
|
||||||||
З ам е ч ан и е 1 . Если s,r ¢, то интеграл òsins x cosr |
xdx отно- |
||||||||||
сится к типу интегралов, рассмотренных в предыдущем пункте, и для его вычисления лучше использовать указанные там подстановки.
З ам е ч ан и е 2 . |
Если s = r ¢, то |
|
|
|
|
|
|
||||||
òsin |
s |
x cos |
r |
xdx = ò |
sins (2x) |
dx = |
1 |
òsin |
s |
t dt . |
|||
|
|
2 |
s |
2 |
s+1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
221

З ам е ч ан и е 3 . Если s,r Î ¥ U{0}, то для понижения степени
целесообразно применять формулы
sin2 x = 12 (1- cos(2x)), cos2 x = 12 (1+ cos(2x)); |
(8.21) |
sin3 x = 14 (3sin x - sin (3x)), cos3 x = 14 (3cos x + cos(3x)); |
(8.22) |
sin4 x = 18 (cos(4x)-4cos(2x)+3), cos4 x = 18 (cos(4x)+4cos(2x)+3),
которые приводят рассматриваемый интеграл к интегралам того же типа, но с меньшими, также неотрицательными целыми степенями.
8.5.3.Интегралы вида òsin(αx) cos(βx)dx ,
òsin(αx) sin(βx)dx , òcos(αx) cos(βx)dx
Интегралы òsin ax cosbxdx , òsin ax sinbxdx , òcosax cosbxdx
непосредственно вычисляются, если их подынтегральные функции
преобразовать по формулам
sin ax cosbx = |
1 |
ésin (a +b)x + sin (a -b)xù, |
|
|
2 ë |
û |
|
sin ax sinbx = |
1 |
écos(a - b) x - cos(a + b)xù , |
|
|
2 |
ë |
û |
cosax cosbx = |
1 |
écos(a -b)x + cos(a + b) xù . |
|
|
2 |
ë |
û |
Пр и ме р 8.33. Вычислим интеграл òsin3 (2x) cos2 (3x)dx. 4Воспользуемся формулами (8.21) и (8.22):
òsin3 (2x) cos2 (3x)dx = 18 ò(3sin (2x) - sin(6x)) (1+ cos(6x))dx =
=-9cos(2x) + cos(6x) + 1 ò(3sin (2x)cos(6x) -sin (6x)cos(6x))dx = 48 8
= |
-3cos(2x) |
+ |
cos(6x) |
+ |
3cos(8x) |
- |
3cos(4x) |
+ |
cos(12x) |
+ C.3 |
16 |
|
128 |
64 |
|
||||||
|
48 |
|
|
182 |
|
|||||
222
Пр и ме р 8.34*. Вычислим интеграл ò |
sin (2n +1) x |
dx . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4Так как sin |
( |
(2n +1)x |
) |
= 2cos |
( |
2nx |
) |
sin x + sin |
(( |
2n -1 x |
) |
, то |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|||||||||
ò |
|
sin ((2n +1) x) |
dx = 2òcos(2nx)dx + ò |
sin ((2n -1)x) |
|
dx = |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
= |
1 sin (2nx) + ò |
sin ((2n -1)x) |
dx. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Обозначив In |
= ò |
sin ((2n +1) x) |
dx , получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n > 0 In |
|
= 1 sin (2nx) + In−1 , |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I0 =nòdx = x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
1 sin |
|
(2kx) + x.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Таким образом, In = å |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=1 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пр и ме р 8.35*. Вычислим интеграл ò |
sin (2nx) |
dx. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
sin x |
|
2n - 2 |
|
x |
|
, то |
|||||||||||||||||||||||||||||||||||||||||||
4Так как sin |
( |
2nx |
) |
= 2cos |
(( |
2n -1 x |
) |
sin x + sin |
(( |
) |
) |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ò |
sin (2nx) |
dx = 2òcos((2n -1) x)dx + ò |
sin ((2n - 2) x) |
dx = |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|||||
= |
|
|
2 |
|
|
|
|
|
sin |
((2n -1) x)+ ò |
sin ((2n - 2) x) |
dx . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
2n -1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Обозначив In |
= |
ò |
|
sin (2nx) |
|
dx, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
n > 1 In |
|
= |
|
|
2 |
|
|
|
sin ((2n −1)x)+ In−1 , |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2n −1 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
sin (2x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
I1 = ò |
|
|
dx = ò2cos xdx = 2sin (x). |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
æ |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, In = åç |
|
|
|
|
|
|
|
sin ((2k -1)x)÷ |
.3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
2k -1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=1 |
è |
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
223
