П. 1.8. Задачи, приводящие к определению частоты появления события в независимых испытаниях. Формула бернулли

Задача 1. Допустим, что на опытной делянке посеяно 15 семян. Примем, что всхожесть всех семян одинакова и равна 80%. Возможны следующие элементарные события:

А₀ = {число семян, давших росток, равно 0};

А₁ = {число взошедших семян равно 1};

А₂ = {число взошедших семян равно 2};

и т. д. и, наконец,

A₁₅ = {все семена дадут всходы}.

Как найти вероятности этих событий, в частности, вычислить вероятность того, что из 15 посеянных семян взойдет ровно 12, безразлично в какой последовательности?

Рассмотрим серию из n независимых испытаний, в каждом из которых некоторое событие А имеет одну и ту же вероятность Р(А) = р, не зависящую от номера испытания.

Такая серия испытаний называется схемой Бернулли.

Решим следующую задачу. В условиях схемы Бернулли определим вероятность P_k,n события, состоящего в том, что при п повторениях испытания событие А, которое имеет одну и ту же вероятность появления в каждом испытании, произойдет ровно k раз безразлично в какой последовательности. Элементарными исходами испытаний являются:

событие = {появление события А в i-м испытании} (i = l, 2, 3, ..., n), P(A_i) = p;

событие = {непоявление события А в i-м испытании} (i=1, 2, 3,..., п), P()=1 –p = g.

Предположим, что событие А имело место в k первых испытаниях и не произошло в п–k последующих, т. е. в соответствии с определением произведения событий, произошло событие A₁A₂A₃...A_k...A_n. Так как испытания независимы, то, применив теорему умножения вероятностей, получим

.

Число способов наступления сложного события, состоящего в появлении события А именно k раз и непоявлении n – k раз равно числу всевозможных множеств, которые можно образовать из п элементов по k элементов, и отличающихся только составом. Число таких множеств

равно [см. формулу (1.2.3)].

Итак, вероятность наступления события А ровно k раз в серии n - испытаний равно

(1.8.1)

Это формула Бернулли. Здесь п – число повторений независимых испытаний; k – число испытаний, в которых событие А произошло (число успехов); р – вероятность появления события А в одном испытании; g - вероятность непоявления события А в одном испытании (g = 1–p); P_k,n – вероятность сложного события, состоящего в том, что при п испытаниях событие А наступило ровно k раз.

Вернемся к сформулированной выше задаче.

1. Число посеянных семян равно числу независимых испытаний, т. е. n = 15,число «успехов» k= 12, p = 0,8, g = 1 – 0,8 = 0,2. Тогда

Событие «12 из 15» имеет небольшую вероятность. Если наблюдать такие серии повторений испытаний, то 12 успехов из 15 испытаний будут иметь место в среднем в 25 сериях из 100.

Вероятнейшее число появлений события при повторении испытаний.

Задача 3. Садовод сделал осенью 6 прививок. По опыту прошлых лет известно, что после зимовки 7 из каждых 10 черенков оставались жизнеспособными. Какое число прижившихся черенков наиболее вероятно?

Решение. Будем условно считать, что вероятность события, состоящего в том, что привитый черенок приживется, одинакова для всех черенков и равна 0,7 и что испытания независимы.

Составим следующую таблицу, учитывая, что p = 0,7, g = 0,3.

Таблица 1.1

Вероятности	Число прижившихся черенков	0	1	2	3	4	5	6
		∙0,36× ×0,70	∙0,7× ×0,35	∙0,72× ×0,34	∙0,73× ×0,33	∙0,74× ×0,32	∙0,75× ×0,3	∙0,76× ×0,30
		0,0007	0,0102	0,0593	0,1852	0,3241	0,3025	0,1176

Из таблицы видно, что наибольшая вероятность соответствует событию, состоящему в том, что приживутся 4 черенка. Следовательно, это событие более возможно, чем все остальные.

Решим задачу в общем виде, не составляя приведенную выше таблицу.

Обозначим число появлений события А, имеющего наибольшую вероятность при п испытаниях, через k₀. Тогда

Р_k0,_n ≥ Р_k0+1,_n (1.8.2)

и

Р_k0,_n ≥ Р_k0+1,_n (1.8.3)

Из (1.8.2) имеем

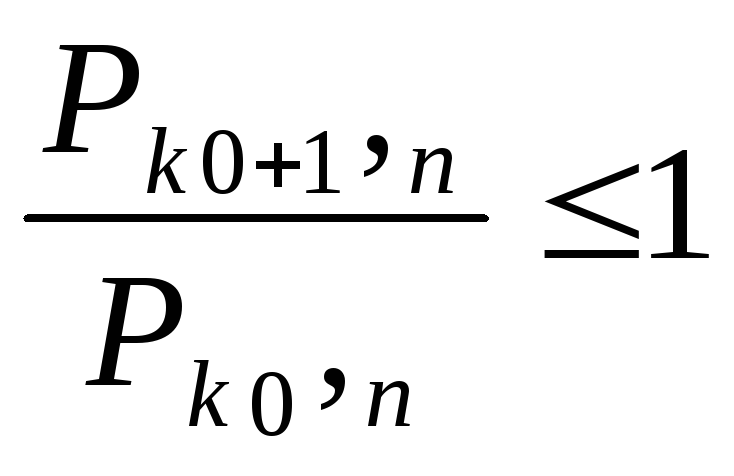
или, учитывая формулу Бернулли (1.8.1),

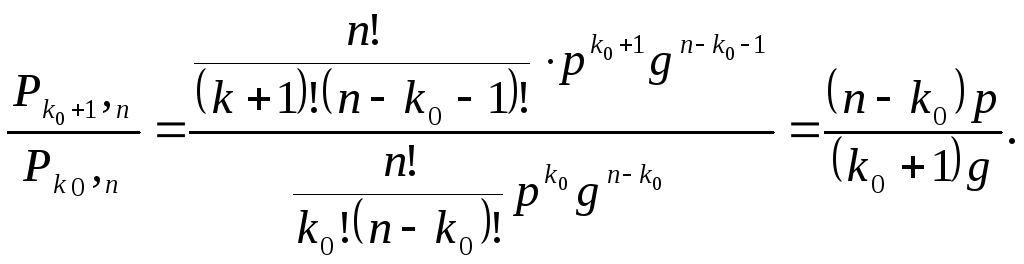(1.8.4)

Из последнего неравенства следует, что

(n – k₀) p ≤ (k₀ + 1) g

После перегруппировки получаем

np – g ≤ k₀ (p + g),

откуда имеем

np – g ≤ k₀ (1.8.5)

Запишем следствие из неравенства (1.8.3)

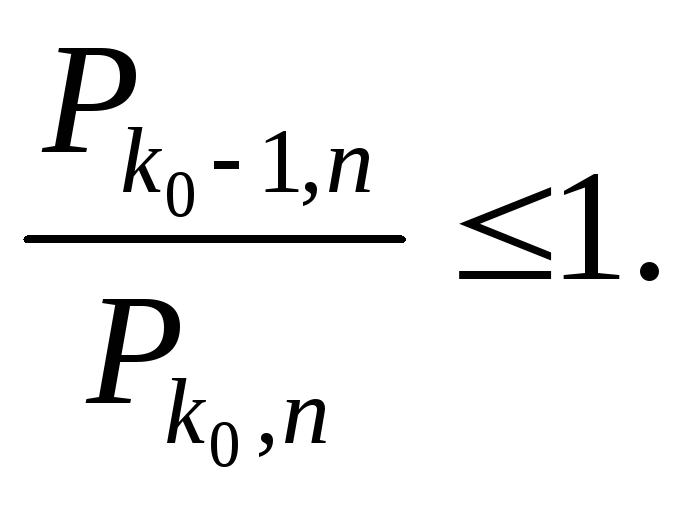
Выполняя те же преобразования, что и для (1.8.2), имеем

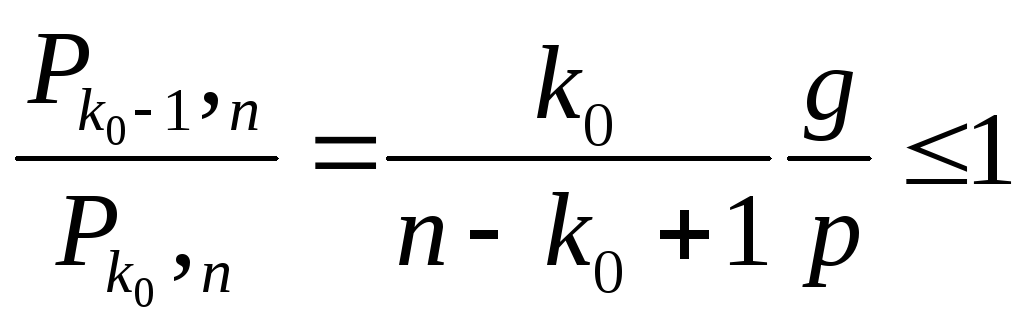
или

k₀ (g + p) ≤ np + p

откуда окончательно получаем

k₀ ≤ np + p (1.8.6)

Объединяя (1.8.5) и (1.8.6), имеем

np–g≤k0≤np+p. (1.8.7)

Числа np–g и np+p отличаются на единицу. Поэтому, если np–g-дробное число, то nр+р - также дробное и неравенство (1.8.7) определяет одно k₀. Если np–g- целое число, то и nр+р - также целое; тогда числа k₀ и k₀+1 будут иметь равную и наибольшую вероятность.

В задаче о садоводе вычислим k₀. Имеем n = 6, p = 0,7, g = 0,3; np–g = 6∙0,7–0,3 = 3,9; np+p = 6∙0,7 + 0,7 = 4,9; 3,9≤k₀≤4,9; k₀ = 4.

п. 1.9. ЛОКАЛЬНАЯ И ИНТЕГРАЛЬНАЯ ТЕОРЕМЫ