П. 2.3. Биномиальное распределение

Пусть случайная величина X есть число k появлений события А при п независимых испытаниях. Вероятность появления события А в каждом испытании постоянна и равна р. Возможные значения случайной величины X числа 0, 1, 2, 3, ..., n. Вероятности появления каждого из этих значений в силу независимости испытаний определяют по формуле Бернулли:

Эти же вероятности можно получить, если воспользоваться формулой бинома Ньютона

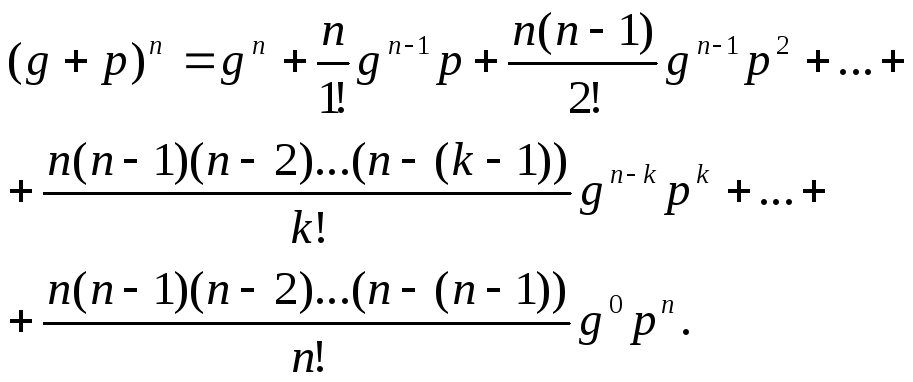
Но

Определение. Закон распределения дискретной случайной величины называется биномиальным, если вероятности возможных ее значений равны соответствующим членам разложения бинома (g+p)ⁿ.

Математическое ожидание биномиального распределения равно

M (X) = np. (2.3.1.)

Дисперсия случайной величины X, распределенной по биномиальному закону, равна npg:

D(X) = npg. (2.3.2)

П. 2.4. Распределение пуассона

Задача 1. Вероятность того, что зерно пшеницы не прорастет, принимается равной 0,01. Какова вероятность того, что из 500 посеянных семян не дадут всходов ровно 8 семян? Не более чем 5 семян?

В этой задаче число семян, не давших всходы - дискретные случайные величины. Заметим, что число испытаний п в задаче велико, а вероятность появления события в каждом испытании мала. Возможные значения случайной величины указать нетрудно, это x₁ = 0, x₂ = 1, x₃ = 2, ..., x₅₀₁ = 500. Вероятность наступления события A k раз, когда п велико, а р мало, определяют по формуле Пуассона, впервые исследовавшего эту задачу:

(2.4.1)

где а - математическое ожидание случайной величины (а = пр); k – число появлений события A (k может принимать только целочисленные значения, теоретически неограниченные, k ≤ n).

Определение. Закон распределения дискретной случайной величины, когда вероятности возможных ее значений находятся по формуле Пуассона (2.4.1), называется распределением Пуассона.

Можно доказать, что для случайной величины X, распределенной по закону Пуассона, ее математическое ожидание равно дисперсии. Это свойство применяется в статистике.

Вернемся к приведенной выше задаче.

1. Имеем п = 500, р = 0,01, g = l – p = 0,99; а = пр = 500∙0,01 = 5. По таблице находим

Вероятность P_8,500 мала. Вероятность того, что не взойдет не более чем 5 семян, равна

Вероятность того, что не взойдет более пяти семян

В случае биномиального распределения случайной величины, когда математическое ожидание мало отличается от дисперсии, т. е. когда np ≈ npg, при решении задач пользуются распределением Пуассона, для данной функции имеются таблицы.

П. 2.5. Непрерывная случайная величина. Интегральная функция (закон) распределения

В п. 2.1 дано определение непрерывной случайной величины. Возможные значения непрерывной случайной величины перечислить нельзя, так как их число бесконечно велико, и поэтому закон распределения в виде таблицы также нельзя составить, если не прибегнуть к упрощениям.

Возьмем бесконечный интервал (–, х), х – произвольное действительное число. Предположим, что в результате испытания случайная величина X приняла одно из значений x₁, x_i(–,x) т.е. оказалось, что Х<х. Событие, состоящее в том, что при одном испытании случайная величина X примет значение, меньшее, чем некоторое число х, имеет определенную вероятность, зависящую от х. Вероятность события = {Х<х} является функцией х:

Р (X < x) = F (x). (2.5.1)

Определение. Интегральной функцией распределения или интегральным законом распределения случайной величины X называется вероятность Р (Х < х) события, состоящего в том, что случайная величина X примет значение, меньшее х.

На числовой прямой равенство P (X < x) = F (x) определяет вероятность попадания случайной точки X левее точки х.

Свойства функции F(x).

1°. F (x) – величина безразмерная и изменяется на множестве [0, 1], т. e. 0 ≤ F(x) ≤ 1, так как F(x) – вероятность события.

2°, F(x) – функция неубывающая, т. е. F (x₁) ≤ F(x₂) при х₁ < х₂.

Свойство очевидно, если принять во внимание геометрический смысл F(x).

3°. P(x₁ ≤ X < x₂) = F (x₂) – F (x₁) (2.5.2)

Доказательство. Событие, состоящее в осуществлении неравенства Х < х₂, может быть представлено как сумма двух несовместных событий:

(Х < х₂) = (x₁ ≤X < x₂) + (X < x₁),

Тогда

P (Х < х₂) = P (x₁ ≤X < x₂) + P (X < x₁),

или

P (x₁ ≤X < x₂) = P (Х < х₂) – P (X < x₁) = F (x₂) – F (x₁).

4° F(–) = 0 и F(+) = 1.

Свойство 4° вытекает из определения (2.5.1). График функции F(x) см. на рис. 1.

Интегральную функцию можно составить и для дискретной случайной величины:

п. 2.6. ДИФФЕРЕНЦИАЛЬНАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ

Возьмем на числовой прямой интервал (х, х + Δх). По формуле (2.5.2) находим

P(x < X <x + Δx) = F(x + Δx) – F(x)

Рис. 2

Определение. Выражение называется средней плотностью вероятности случайной величины на интервале [x, x+Δx]

Определение. Предел средней плотности вероятности при Δx→0 называется дифференциальной функцией или плотностью распределения вероятностей непрерывной случайной величины и обозначается f(x),

Кривая, соответствующая уравнению y = f(x), называется кривой вероятностей и может иметь вид, изображенный на рис. 2.

Свойства функции f(x).

1°.f(x) ≥ 0 как производная от неубывающей функции.

2°.

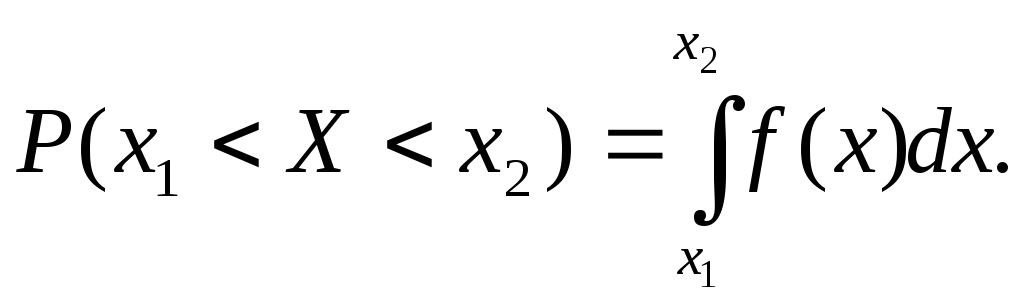(2.6.1)

Доказательство. Имеем (рис. 3)

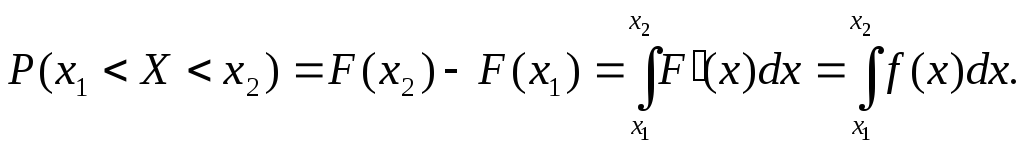
3°.

(2.6.2)

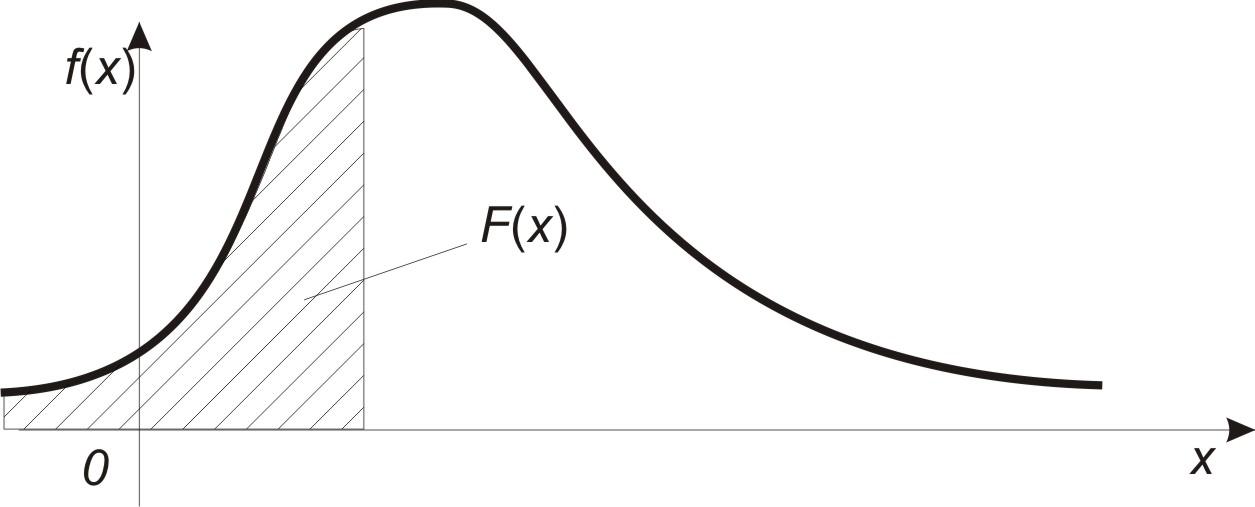
Доказательство. Имеем (рис. 121)

(2.6.3)

4°.

(2.6.4)

Доказательство. Находим

5°. Если возможные значения случайной величины принадлежат замкнутому промежутку, т. е.

то

(2.6.5)