П. 2.9. Вероятность попадания

Нормально распределенной случайной

Величины в заданный интервал.

Правило трех сигм

Пусть дан интервал α<Х<β. Вероятность того, что случайная величина, подчиненная нормальному закону с параметрами а и σ, попадает в этот интервал, равна

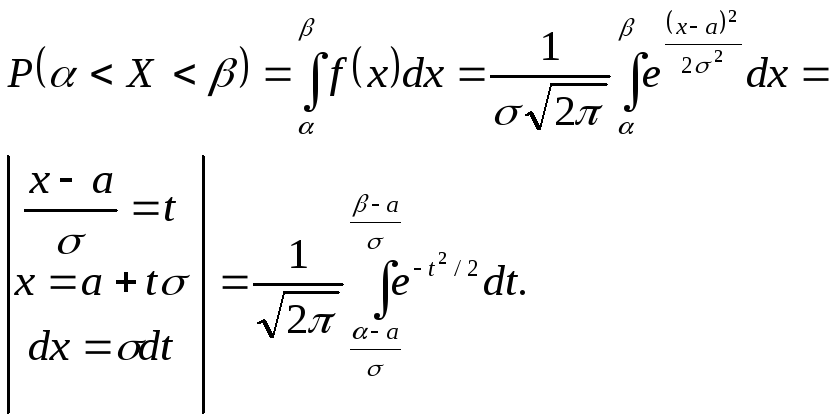
Учитывая, что

Найдем

(2.9.1)

где Ф (х) - функция Лапласа,

Рассмотрим частный случай. Пусть необходимо найти вероятность попадания случайной величины в интервал, симметричный относительно математического ожидания. Учитывая (2.9.1), имеем

Так как то

(2.9.2)

Вычислим теперь вероятности:

1) (2.9.3)

2) (2.9.4)

3) (2.9.5)

Результаты вычислений по формуле (2.9.5) показывают, что вероятность отклонения случайной величины X от М(Х) меньше чем на 3σ близка к 1.

Правило трех сигм. Практически достоверно, что при однократном испытании отклонение нормально распределенной случайной величины от ее математического ожидания не превышает утроенного среднего квадратического отклонения.

Это правило часто используется в математической статистике.

П. 2.10. Понятие о законе больших чисел

Теория вероятностей обобщает реальные свойства случайных явлений и величин. Важным в процессе обобщения является выражение объективно существующих закономерностей в виде закона больших чисел.

Используя понятие случайной величины, математического ожидания и дисперсии П. Л. Чебышев сформулировал, а А. А. Марков дополнил закон больших чисел.

Определение. Говорят, что последовательность случайных величин

X₁, X₂, X₃, … X_п (2.10.1)

имеющих математические ожидания М (Х₁), М (Х₂), М (Х₃), ..., М (Х_п), подчиняется закону больших чисел, если среднее арифметическое этих случайных величин при n→ с вероятностью, неограниченно приближающейся к 1, сколько угодно мало (меньше чем на ε > 0) отличается от среднего арифметического их математических ожиданий, т. е. при n→:

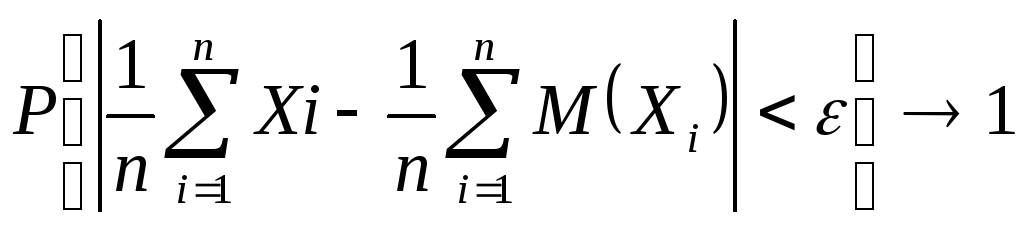(2.10.2)

Общие условия, которым должны удовлетворять случайные величины Х₁, Х₂, Х₃, ..., Х_п, достаточные для большинства практических встречающихся случаев, были найдены П. Л. Чебышевым, а затем еще более расширены А. А. Марковым. Кратко они формулируются так.

Теорема Чебышева. Если величины Х₁, Х₂, Х₃, ..., Х_п, попарно независимы и их дисперсии D (X)_i ограничены, т. е. D (X _i) ≤ C, где С – некоторое число, не зависящее от п, то предельное равенство (2.10.2) выполняется, т. е. для Х₁, Х₂, Х₃, ..., Х_п справедлив закон больших чисел.

Теорема Бернулли. Пусть производятся п испытаний, в каждом из которых событие А может появиться с одной и той же вероятностью р. Обозначим через x_i число появлений события А в i-м испытании. Возможные значения x_i: x_i = 1, если событие А наступило, и x_i = 0, если А не произошло в этом испытании. Сумма х₁ + х₂ + х₃ + ... + х_п = т есть число появлений А в п испытаниях. Тогда

M (x_i) = 1∙p + 0 (1-p) = p,

(Можно доказать, что если p + g = l, то max pg = l/4.) Условия ограниченности дисперсии выполнено. Поэтому к случайной величине x_i применим закон больших чисел.

Подставив в (12.10.2) вместо число и вместо число пр, получим

, при n→ (2.10.3)

т. е. с вероятностью, сколь угодно близкой к единице, можно утверждать, что при числе испытаний n→ относительная частота появления события в одном испытании сколь угодно мало отличается от его вероятности. Это и есть доказательство теоремы Бернулли, как частного случая закона больших чисел, сформулированного П. Л. Чебышевым.

Закон больших чисел имеет важное практическое значение. Именно, на этом законе основано утверждение, что среднее арифметическое результатов измерений считается наиболее точным, наиболее близким к истинному значению измеряемой величины. Закон больших чисел широко используется в статистике, на нем основан выборочный метод, рассмотренный в следующей главе.