3. Теорема сложения вероятностей для случая, когда события совместны.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий, минус вероятность их совместного появления, т. е.

P(A+B)=P(A)+P(B)–P(AB) (1.6.8)

По определению событие А+В состоит в наступлении или события, или события, или событияАВ, следовательно,

.

События, стоящие в правой части равенства, несовместны: появление одного из них исключает появление остальных. Поэтому

(1.6.9)

Но Следовательно,Подставим эти значения в (1.6.9). Имеем

P(A+B)=P(A)+P(B)–P(AB). (1.6.10)

Пример 2. В посевах пшеницы на делянке имеется 95% здоровых растений. Выбирают два растения. Определить вероятность того, что среди них хотя бы одно окажется здоровым.

Пусть события А₁ = {первое растение здоровое}; событие А₂ = {второе растение здоровое}; событие А₁+А₂ = {хотя бы одно растение здоровое}. Так как события А₁ и А₂ совместны, то

Событие А₁+А₂ практически достоверно. Задачу можно решить и другим способом. При повторных испытаниях, как это имело место в задаче, появление хотя бы одного события (А₁ + А₂) и непоявление события ни разу ()- события противоположные; тогда

Как мы видим, получен один и тот же результат.

П. 1.7. Теорема полной вероятности. Формула байеса

Приведенная ниже формула объединяет теоремы сложения и умножения. Вероятность события A, которое может произойти при условии осуществления одного из несовместных событий В₁, В₂, В₃, ... B_n, образующих полную группу, определяется формулой

(1.7.1)

Для наступления события A необходимо и достаточно наступления или события AB₁, или события АВ₂, или события АВ₃, ..., или события AB_n,

А=АВ₁+АВ₂+АВ₃+…+АВ_п

Так как события АВ_i несовместны, то поэтому(1.7.2)

Пример. Азотное удобрение поступает на склад хозяйства из пункта 1 и пункта 2, причем, из 1-го пункта в 2 раза больше, чем из 2-го. Вероятность события = {удобрение из первого пункта удовлетворяет стандарту}0,9, а соответствующая вероятность для второго пункта равна 0,7.Определить вероятность события А = {взятое для пробы на складе хозяйства удобрение удовлетворяет стандарту}.

Решение. Обозначим

событие В1 = {удобрение поступило из пункта 1};

событие В2 = {удобрение поступило из пункта 2};

Находим

, ,,;

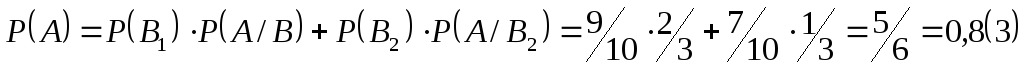
Событие А имеет большую вероятность, оно практически достоверно, т. е. наступит в среднем в 83 случаях из 100.

Формула Байеса. Рассмотрим следующую задачу. На фермах А и В произошла вспышка заболевания ящуром. Доли заражения скота составляют соответственно 1/6 и 1/4. Случайным образом отобранное из одной фермы животное оказалось заболевшим. Найти вероятность события = {животное выбрано из фермы А}. Обозначим:

А = {отобранное животное заражено};

событие В1 = {животное выбрано из фермы А}, Р(B₁) = 0,5;

событие В2 = {животное выбрано из фермы В}, Р(B₂) = 0,5;

А/В₁ = {животное, отобранное из фермы А, заражено};

A/B₂ = {животное, отобранное из фермы В, заражено}.

Вероятность события = {животное выбрано из фермы А и заражено} можно записать в виде Р(А)∙Р(В₁/А) = P(B₁)∙Р(А/В₁), откуда

(*)

или

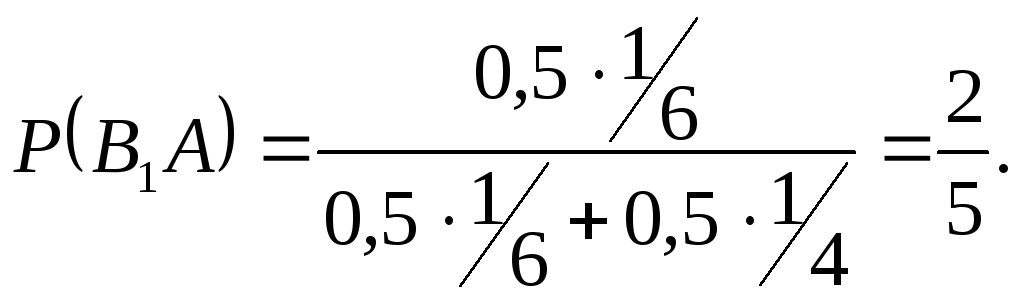
Заменив в () Р(А) на , получим

• ()

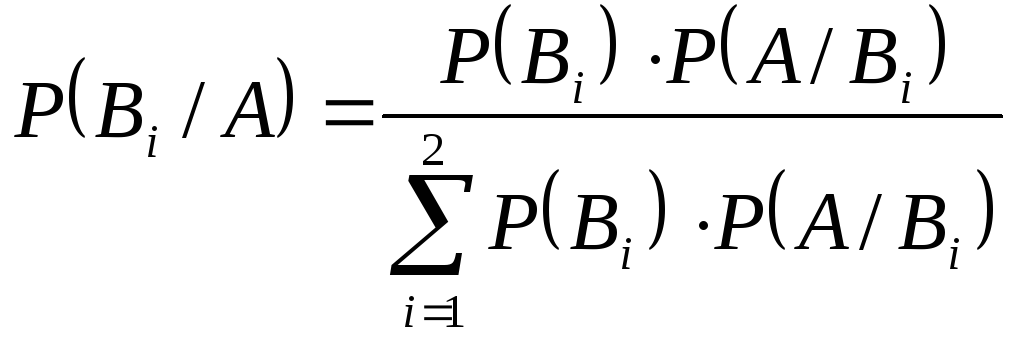Формула (**) является частным случаем формулы Байеса.

Рассмотрим задачу в общем виде. Пусть в результате испытания произошло событие А, которое могло наступить только вместе с каждым из событий B₁, В₂, В₃,..., В_п, образующих полную группу; P(B₁), Р(В₂), ... , Р(В_п) заранее известны. Требуется найти вероятности событий В₁, B₂,..., В_п после испытания, когда событие А уже имело место, т. е. P(B_i/A), i=1, 2, ..., п.

Проводя рассуждения, аналогичные приведенным при решении задачи, получим формулу

(1.7.3)

Эта формула называется формулой Байеса. По формуле (1.7.3) можно вычислить вероятности событий В_i, когда событие А произошло, т. е. переоценить вероятности.