18.2. Метод оберненої матриці.
Одним з прямих методів розв’язання системи лінійних рівнянь є метод оберненої матриці. Розглянемо систему n лінійних рівнянь з n невідомими. Складемо матрицю системи із коефіцієнтів при невідомих і матриці-стовбці невідомих і вільних членів:
,
,
.
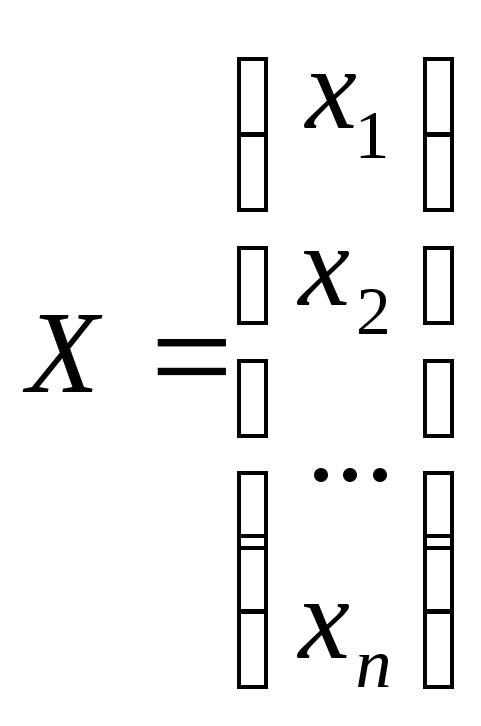Представимо задану систему в еквівалентному матричному вигляді.
Помножимо
обидві частини даного рівняння на
обернену матрицю (A-1),
вважаючи,
що матриця системи A
невироджена
.
,
,
– розв’язок матричного рівняння і
початкової системи.
Приведемо фрагмент вирішення системи лінійних рівнянь матричним способом.
…………………………………………………………………
void main()
{
double k[9]={
1, 0, 8,
2, 5, 9,
3, 6, 0
};
double cc[9],dd[3];
double aaa[3]={6, 4, 9};
mObr_Gauss(k,cc,3);
mumnog(cc, aaa, 3, 3, 1, dd);
cout<<"\n\n"<<cc[0]<<"\t"<<cc[1]<<"\t"<<cc[2];
cout<<"\n"<<cc[3]<<"\t"<<cc[4]<<"\t"<<cc[5];
cout<<"\n"<<cc[6]<<"\t"<<cc[7]<<"\t"<<cc[8];
cout<<"\n\nx1="<<dd[0]<<"\tx2="<<dd[1]
<<"\tx3="<<dd[2];
}
…………………………………………………………………
У результаті виконання програми, використовуючи функції mObr_Gauss() для обчислення оберненої матриці, та функції mumnog() для множення матриць знайдено обернену матрицю (сс) та корені рівняння (dd):
0.692308 -0.615385 0.512821
-0.346154 0.307692 -0.0897436
0.0384615 0.0769231 -0.0641026
x1 = 6.30769 x2 = -1.65385 x3 = -0.0384615
18.3. Метод Крамера
Розглянемо систему n лінійних рівнянь з n невідомими.
будемо
називати визначником системи.
Нехай
:
Якщо визначник системи ∆ відмінний від нуля то ця система має лише один розв’язок, який знаходять по наступним формулам:
∆xi – це визначник системи, у якому необхідно замінити коефіцієнти, що стоять попереду невідомого xi на стовбець вільних членів.
Наведемо фрагмент реалізації системи лінійних рівнянь з 3-ма невідомими методом Крамера.
…………………………………………………………………
void main()
{
double d,dx1,dx2,dx3,x1,x2,x3;
double k[9]={
1,0,8,
2,5,9,
3,6,0
};
/*
double aaa[3]={
6,
4,
9
};
*/
double aax1[9]={
6,0,8,
4,5,9,
9,6,0
};
double aax2[9]={
1,6,8,
2,4,9,
3,9,0
};
double aax3[9]={
1,0,6,
2,5,4,
3,6,9
};
d = mopred(k, 3);
dx1 = mopred(aax1, 3);
dx2 = mopred(aax2, 3);
dx3 = mopred(aax3, 3);
x1 = dx1/d;
x2 = dx2/d;
x3 = dx3/d;
cout<<"\nx1="<<x1<<"\tx2="<<x2<<"\tx3="<<x3;
}
…………………………………………………………………
У результаті виконання програми, будуть виведені наступні результати:
x1 = 6.30769 x2 = -1.65385 x3 = -0.0384615
18.4. Метод Гауса
Метод Гауса – це метод послідовного виключення невідомих. Він є самим швидким методом розв’язку системи лінійних рівнянь порівняно з методами оберненої матриці та методом Крамера. Нехай задана система n лінійних рівнянь з n невідомими. Складемо розширену матрицю системи.
Шляхом елементарних перетворень із матриці B побудуємо трикутну матрицю. Ця система має лише один розв’язок (визначник не повинен дорівнювати нулю). Невідомі знаходяться шляхом розв’язку у зворотному порядку.
Нижче приведемо фрагмент програми, за допомогою якого вирішується система лінійних рівнянь використовуючи метод Гауса.
#include <iostream>
#include <cmath>
using namespace std;
# define delta 0.00000001
// aaa - массив свободных членов
// bb - выходной массив
bool mGauss(double*k,double*aaa,double*bb,int n)
{
int i,j,xx,r,kol_el;
double t,vv;
kol_el = n*n;
//Якщо визначник 0 - система має безліч коренів.
if(fabs(mopred(k,n))<delta)return false;
double*aa = new double[n];
double*kk = new double[kol_el];
//Перегонка масивів
for(i=0;i<n;i++)
aa[i] = aaa[i];
for(i=0;i<kol_el;i++)
kk[i] = k[i];
// Перетворення коефіцієнтів рівняння до
// трикутного виду
// нижній трикутник 0
// переставляються та продвигаються рядки (також
// як і в методиці знаходження визначника,
// тільки стовбці замінені на рядки, так як
// кожному рівнянню відповідає визначений рядок
// матриці
for(j=0;j<n;j++)
for(i=n-1;i>j;i--)
{
if (fabs(kk[(i-1)*n+j])<delta)
{
for(xx=j;xx<n;xx++)
{
vv = kk[i*n+xx];
kk[i*n+xx]=kk[(i-1)*n+xx];
kk[(i-1)*n+xx] = vv;
}
vv = aa[i];aa[i] = aa[i-1];aa[i-1] = vv;
continue;
}//endif
if (fabs(kk[i*n+j])<delta)continue;
t = kk[i*n+j]/kk[(i-1)*n+j];
for(r=j;r<n;r++)
kk[i*n+r]=kk[i*n+r]-kk[(i-1)*n+r]*t;
aa[i]=aa[i]-aa[i-1]*t;
}
/* Знаходження коренів рівняння обратним ходом (знизу вверх)
по зміні матриці невідомих та масиву вихідних членів
*/
for (i=n-1;i>=0;i--)
{
for (j=n-1;j>i;j--)
aa[i]-=kk[i*n+j]*aa[j];
aa[i]/=kk[i*n+i];
}
for(i=0;i<n;i++)bb[i] = aa[i];
delete[]aa;
delete[]kk;
return true;
}
void main()
{
double k[9]={
1, 0, 8,
2, 5, 9,
3, 6, 0
};
double bb[3];
double aa[3]={6, 4, 9};
mGauss(k,aa,bb,3);
cout<<"\nx1="<<bb[0]<<"\x2="<<bb[1]
<<"\tx3="<<bb[2];
}
У представленій функції mGauss() спочатку перевіряється визначник матриці коефіцієнтів рівняння (масив k). Якщо він не дорівнює нулю, матриця за допомогою алгоритму описаному вище (при отриманні визначника) – зводиться до трикутної форми (нижній трикутник заповнюється нулями). Відмінність полягає в тому, що операції здійснюються не над стовпчиками, а над рядками, так як кожен рядок характеризує відповідне рівняння. Крім того, розглядається ще й масив вільних членів (aaa). Після приведення матриці до трикутної форми – у зворотному порядку знаходяться корені рівняння. Серед прямих методів розв’язку системи лінійних рівнянь метод Гауса є самим швидким та оптимальним.
У результаті виконання програми одержимо корені рівняння на екрані дисплею:
x1 = 6.30769 x2 = -1.65385 x3 = -0.0384615
14