
ODM_Лекции
.pdf
71
у6(x1, x2) = x1 x2 y7(x1, x2) = x1 x2
|
|
|
|
|
|
x1 |
|
|
x1 |
1 |
|
|
|
|
|||
x2 |
у6 |
|
x2 |
1 |
у9 |
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
Выразим в заданном базисе функцию отрицания у6(x, 1) = x
Выразим функцию конъюкции у6 (y7(y6, 1), у6(x2, 1),1) = x1x2
Запишем выражение искомой функции
f ( x1, x2, x3 ) = y7 [у6 (y7(y6(x2, 1), y6(x3, 1)),1),y6(y7(x2,x3),1), y6(y7(x1, y6(x2,1)),1)];
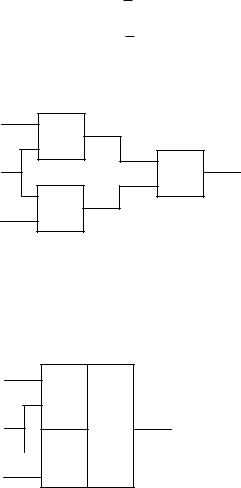
Построим схему данной функции :
1 |
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
1 |
|
|
|
|
1 |
|||
|
|
|
|
||||||
1 |
|
1 |
|
f ( x1, x2, x3 )
|
|
|
x3 |
1 |
|
|
||
|
|
|
1 |
|
|
|
|
1
1
x2
x3
1
1
1 |
|
1 |
|
x2
x3
Если число аргументов функций велико, то описанный способ синтеза комби-
наторных схем становится громоздким и трудоемким.
Для синтеза схем с большим числом переменных существуют более эффек-
тивные методы. Один из них :
МЕТОД КАСКАДОВ.
72
Основанием для метода является теор. Шиннона, исходя из которой произв.
Функция может быть представлена в следующем виде :
f(x1, … , xn) = x i f(x1, …, xi-1, ,xi+1, …, xn)+f (x1, …,xi-1,1,xi+1,…, xn ) = = x i f ( ) + xi f( 1 )
Эту функцию можно реализовать следующей схемой :
f1
&
xi
1 |
f |
&
f0
Это устройство – каскадный элемент, который на схемах обозначают в следу-
ющем виде :
f1 &
1
x1 |
& |
f |
|
|
|
|
|
f0
С помощью данного каскада получено представление от n аргументов, через остат-ные функции f0 и f1 для функций от n-1 аргумент, с помощью искл. хi
перемен.
На втором шаге каскада реализуется искл. следующая перемен. И далее по-
ступая также мы получим остат – ные функции.
Это – каскадный метод – при этом каждый каскад соответствует исключению некоторой переменной. Для одной и той же функции можно получить не-
сколько реализаций. Число реализаций равно :
N ( N - 1)( N – 2) - … = n!
Отсюда следует, что найти самую эффективную реализацию простым перебо-
ром весьма затруднительно.

73
Поэтому для метода должна быть найдена эффективная стратегия. Это позво-
ляет сделать аппарат произв – ных от булевых функций. Пр – ная от функции n-аргументов.
f(x1 , x 2 ,...,x n |
) |
=f (x1,…, xi-1, ,xi+1,…, xn) f (x1, …, xi-1,1,xi+1, …, xn) |
x1 |
|
|
|
|
|
Пример : |
|
|
Найти пр-ную от функции двух переменных f (x1,x2) = x1 + x2
f(x1 |
, x 2 ) |
|
|
|
|
|
= x2 |
(1 + x2) = x 2 |
|||||
x1 |
||||||
|
|
|
|
|||
Повторные пр-ные определяются следующим образом :
2 f |
|
= |
|
|
( |
|
f |
) и т. д. |
||
x |
i |
x |
j |
x |
i |
x |
j |
|||
|
|
|
|
|
|
|
||||
Пр-ная от булевой функции определяет условия при которых функция зависит
от хi
f (x1,…, xi-1, ,xi+1,…, xn) f (x1, …, xi-1,1,xi+1, …, xn) т.е. при изменении хi ме-
няется значение функции. ( функция зависит от перем.)
Если пр-ная равна 0, то функция от хi не зависит, т.е. при изменении хi значе-
ние функции не меняется.
Рассмотрим пример:
f (x1, x2, x3, x4) = x1x2x3 + x 1х4 + x2x3 + x1 x 3x4
Определить при каких условиях функция зависит от переменной х3. Найдем соответствующую производную :
f = ( x 1х4 +х1х4) (х1х2 + x 1х4 +х2) = х4 ( х2+ x 1х4) =
x 3
= х4 x 2 x 1х4 + x 4 ( х2+ x 1х4 ) = х4 x 2 (х1+ x 4) + x 4х2 = x 4х2 + х4 x 2х1
Ответом на поставленную задачу будут значения х1, х2 , х4 при которых

74
f = 1.
x 3
Составим соответствующую таблицу:
х1 |
х2 |
х4 |
|
f |
|
|
|
|
|
x 3 |
|
0 |
0 |
0 |
|
0 |
|
0 |
0 |
1 |
|
0 |
|
0 |
1 |
0 |
|
1 |
|
0 |
1 |
1 |
|
0 |
|
1 |
0 |
0 |
|
0 |
|
1 |
0 |
1 |
|
1 |
|
1 |
1 |
0 |
|
1 |
|
1 |
1 |
1 |
|
0 |
|
|
|
|
|
|
|
х1 |
х2 |
х4 |
|
f |
|
|
|
|
|
x 3 |
|
|
|
|
|
|
|
0 |
1 |
0 |
|
1 |
|
1 |
0 |
1 |
|
1 |
|
1 |
1 |
0 |
|
1 |
|
На этих наборах функция зависит от переменной х3. Первый шаг каскадной реализации.
х1 |
& |
|
& |
1 |
|
х4
&
f0
f0 ( x1,x3,x4 ) = x 1 + x 3 x 4 + x3x4 = x 1 + x3 x4
Введем определение :

75
Весом пр-ной функции называется количество возможных наборов, при кото-
рых производная равна 1. Исходя из предыдущего примера сложность произ-
водной по х3 ( |
f |
) равна 3. |
|
|
|
||
x |
3 |
||
|
|
|
|
Запишем утверждение :
Чем больше состояний имеет функция, прикоторых она зависит от xi, тем сильнее она зависит от этой переменной.
Для примера выясним от какой переменной функция зависит сильнее. f ( x1, x2, x3,x4 ) = x1x2x3 + x 1x4 + x2x3 + x1 x 3x4
W ( |
|
f |
) = 3 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
3 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
||||||
= ( x4 +x2x3 ) (x2x3 + |
x |
3x4 ) |
|
|
|
|
|
||||||
x |
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х1 |
х2 |
х4 |
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
0 |
0 |
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
0 |
1 |
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
1 |
0 |
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
1 |
1 |
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
0 |
0 |
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
0 |
1 |
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
1 |
0 |
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
1 |
1 |
|
0 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W ( |
f |
) = 1 |
|
|
|
|
|
|
|
|
|
|
||||
x |
||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
3x4 ) ( x1x3 + |
|
|
|
|
|
|
|
3) ( x3 + x4 ) |
|||
|
|
= ( |
x |
1x4 + x1 |
x |
x |
1x4 + x3 + x1 |
x |
3x4 ) =(x4 |
x |
1 + x4 |
x |
||||
|
x 2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

76
|
|
|
|
|
|
х1 |
х2 |
|
х4 |
|
f |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
W ( |
f |
) = 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|||||||||||
|
=(x1x2x3 + x2x3) (x1x2x3 + |
x |
1 + x2x3 |
+ x1 |
x |
3) = x2x3 (x2 + |
x |
1 + |
x |
3 ) |
|||||||||||
|
x 4 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
х1 |
х2 |
|
х4 |
|
f |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W ( f ) = 5
x 4
77
Оказалось, что сильнее всего функция зависит от переменной х4. При этом видно, что чем сильнее зав-ть функции, тем меньше сложность ост-ной функ-
ции при ее искл-нии.
Для функции заданной таблично удобно использовать следующий метод определения веса производной:
Рассмотрим на примере :
Функция от четырех переменных задана таблицей истинности :
х1 |
х2 |
x3 |
x4 |
f |
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
|
|
|
|
|
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
|
|
|
|
0 |
1 |
0 |
1 |
1 |
|
|
|
|
|
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
0 |
1 |
1 |
1 |
1 |
|
|
|
|
|
1 |
0 |
0 |
0 |
1 |
|
|
|
|
|
1 |
0 |
0 |
1 |
0 |
|
|
|
|
|
1 |
0 |
1 |
0 |
1 |
|
|
|
|
|
1 |
0 |
1 |
1 |
0 |
|
|
|
|
|
1 |
1 |
0 |
0 |
1 |
|
|
|
|
|
1 |
1 |
0 |
1 |
1 |
|
|
|
|
|
1 |
1 |
1 |
0 |
0 |
|
|
|
|
|
1 |
1 |
1 |
1 |
0 |
|
|
|
|
|
Для заданной функции определить веса производных по х1, х2, х3, х4.
78
x2 |
x3 |
x4 |
1 |
0 |
d |
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
0 |
1 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
0 |
1 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
1 |
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
1 |
0 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
1 |
1 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
Cтолбцы 1 и 0 заполняются следующим образом :
Вместо искл. переменной в каждый набор подставляются значения 1 или 0 и
выписывают соотв. стб. знач. Функции из исходной таблицы.
Столбец d получается сложением по mod 2 соотв. знач. стб. 1 и 0.
W1 = 5 x2 :
x1 |
x3 |
x4 |
1 |
0 |
d |
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
0 |
1 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
0 |
1 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
1 |
0 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
1 |
0 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
1 |
1 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
W2 = 3

79
x3 :
|
x1 |
x2 |
x4 |
1 |
0 |
d |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
0 |
1 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
1 |
0 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
W3 = 3 |
|
|
|
|
|
|
x4 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
x3 |
1 |
0 |
d |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
0 |
1 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
1 |
0 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
W4 = 5
Анализ производных показал, что для данного примера первыми исключ-ми переменными будут х1 и х4.
Рассмотрим более сложную задачу для которой функция задана аналитически
( от 5-и переменных ).
f ( x1, x2, x3, x4, x5 ) = x1 x 2x3 + x 1 x 3x4 + x1x3 x 5 + x1x2x4 + x 2x3x5 + x 3 x 4x5

80
Для данного примера на картах Карно определим веса производных и первую искл. переменную. Затем на картах Карно определим вторую исключаемую переменную и т.д., а затем по полученным данным построим принц. Схему функции.
X1X2 x3X4X5 |
001 |
011 |
010 |
110 |
111 |
101 |
100 |
|
00 |
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
|||||
01 |
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
11 |
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|
1 |
1 |
|
|
|
|
||||||
10 |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
1 |
1 |
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
W1 = 7 ; W2 = 5 ; W3 = 9 ; W4 = 5 ; W5 = 7 ;
Первая искл. переменная х3
Рассмотрим карту Карно для остальных функций : f ( 1 ) f ( 0 )
X1X2 |
X4X5 00 |
01 |
11 |
10 |
|
f (0) |
00 |
|
|
|
|
|
1 |
1 |
1 |
||
|
|
|
|||
|
01 |
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|||
|
11 |
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|||
|
10 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W1 = 2 ; W2 = 2 ; W4 = 4 ; W5 = 4 ;
X1X2 |
X4X5 00 |
01 |
11 |
10 |
|
f (1) |
00 |
|
|
|
|
|
1 |
1 |
|
||
|
|
|
|
||
|
01 |
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
1 |
|
1 |
1 |
|
|
|
|
|||
|
10 |
|
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
||||
|
|
|
|
|
|
W1 = 5 ; W2 = 3 ; W4 = 1 ; W5 = 3 ; Искл. х1
