2

Министерство образования и науки украины

ГВУЗ «ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Методические указания и задания

к лабораторным работам

по курсу “Основы дискретной математики“, часть II

(для студентов, обучающихся по направлению подготовки “Компьютерные науки”)

Донецк – 2011

УДК 518.551071

Методические указания и задания к лабораторным работам по курсу “Основы дискретной математики” (для студентов, обучающихся по направлению подготовки “Компьютерные науки”) / сост.: И.А. Назарова. – Донецк: ДонНТУ, 2010. - 74с.

Приведены теоретические сведения, методические рекомендации, контрольные вопросы и задания для выполнения лабораторных работ по разделу дискретной математики: теория графов.

Составители: Назарова И. А., доцент каф. ПМИ

Рецензент: Теплинский С. В., к.т.н., доц. КИ

Лабораторная работа № 1

Подграфы и изоморфизм.

Цель работы: изучение основных понятий теории графов и приобретение практических навыков определения изоморфизма графов, построение подграфов, независимых множеств и клик.

Теоретическая справка

Пусть V – некоторое непустое множество (V  ).

V⁽²⁾ – множество всех его двухэлементных подмножеств (V⁽²⁾={(u,v)|u,vV,неупорядоченная пара}).

Неориентированный граф G – пара множеств (V,E), E  V⁽²⁾ ,

где V – множество вершин графа G,

E – множество рёбер графа G.

Если |V|=p, а |E|=q, то обозначают граф G – (p, q)- граф или p-граф.

Смежные вершины графа G – вершины, соединенные ребром.

Смежные ребра графа G – ребра, имеющие общую вершину.

Инцидентные ребро и вершина – вершина является одним из концов ребра.

Конечный граф – множество вершин графа конечно.

Способы задания графов

1. Перечисление вершин V и ребер E.

2. Графически: прообраз вершины – точка, прообраз ребра – отрезок.

3. Матричные способы описания.

1. Матрица смежности.

A=||a_ij||, i,j=1.. p, |V|=p, |E|=q.

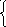1, если существует ребро (i,j);

a_ij =

0, иначе .

2. Матрица инцидентности.

B=||b_ij||, i=1.. p, j=1.. q, |E|=q, |V|=p.

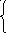
1, вершина i инцидентна ребру j;

b_ij =

0, иначе.

Например:

Задан граф G=(V, E), где

V={a, b, c, d},

E={ab, bc, ac, ad, dc}.

Матрица смежности

	a	b	c	в
A= B= a	0	1	1	1
b	1	0	1	0
c	1	1	0	1
d	1	0	1	0

Матрица инцидентности

	ab	bc	ac	ad	dc
a	1	0	1	1	0
b	1	1	0	0	0
c	0	1	1	0	1
d	0	0	0	1	1