Степени вершин графа

Степень вершины deg(v) графа G – число инцидентных ей ребер.

Максимальная степень всех вершин графа G – (G):

(G)=MAX deg(v) .

vV

Минимальная степень всех вершин графа G – (G):

(G) = MIN deg(v) .

vV

Лемма о рукопожатиях.

Сумма степеней всех вершин графа g четна и равна удвоенному числу ребер.

Изолированная вершина графа G – вершина, степень которой равна 0.

Висячая вершина графа G – вершина, степень которой равна 1.

Доминирующая вершина графа G – вершина, степень которой равна p-1, где p – количество вершин графа G.

Например:

доминирующей нет

висячие - v₃, v₄

изолированная - v₅

Экстремальные графы

Полный граф – любые две вершины смежные. Обозначается, K_n.

Например:

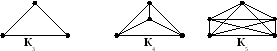
Пустой граф – не имеет ребер. Обозначается через O_n .

Мультиграф – граф, не содержащий петель, но с кратными ребрами.

Псевдограф – граф, содержащий петли и кратные ребра.

Например:

Нуль-граф – граф без вершин и без ребер.

Тривиальный граф – граф с одной вершиной (1,0 -граф).

Однородный или регулярный граф – все вершины имеют равную степень.

Н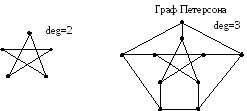апример:

Двудольный граф – множество вершин графа можно разбить на два непересекающиеся подмножества V₁ и V₂ таких, что каждое ребро имеет одну концевую вершину в V₁, а вторую – в V₂, причем V₁V₂=, а V₁V₂=V.

Полный двудольный граф – двудольный, у которого любые две вершины, входящие в разные доли, смежные. Обозначается K_{p, q}.

Звезда – полный двудольный граф, у которого p=1. Обозначается K_1,q.

Биграф - двудольный граф.

Например:

Звезда K_1,3

Полный двудольный граф K_3,3

Двудольный граф

Граф G(V,E) называют k-дольным, если множество его вершин V можно разбить на такие подмножества V_i , i= 1..n , что любое ребро графа имеет одну концевую вершину в V_i , а другую - V_j , причём V_i V_j = , i  j, i,j=1..n, а V_i=V.

Например:

Изоморфизм графов.

Изоморфные графы – существует взаимноодназначное соответствие, т. е. биекция, между множествами их вершин, сохраняющая отношение смежности.

Изоморфизм графов G и H : G  H.

Например:

Заданы два графа G₁, G₂. Определить изоморфизм G₁, G₂, построив биекцию их вершин.

Решение:

Граф G₁ изоморфен графу G₂, потому что существует биекция : V₁  V₂, сохраняющая отношение смежности.

Биекция : u  V1	a	b	c	d
 (u)  V2	c	d	b	a

Например:

Изоморфны

Изоморфизм есть отношение эквивалентности, т. к. он:

• симметричен;

• рефлексивен;

• транзитивен.

Подграфы

Помеченный граф – граф, у которого каждой вершине поставлена в соответствие некоторая уникальная отметка (символ, цифра), иначе – абстрактный .

Дополнение графа G - граф G' = (V', E'), такой, что V=V', а E'= V⁽²⁾ \ E (вершины смежные в G' не смежны в G и наоборот).

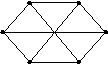
Подграф G₁ = (V₁, E₁) графа G = (V, E) – граф, у которого все вершины и ребра удовлетворяют следующим соотношениям V₁  V, E₁  E.

Остовный подграф графа G - подграф, содержащий все вершины графа G, множество ребер есть подмножество ребер графа G.

Порожденный подграф ( порожденный подмножеством вершин V₁) – подграф, множество вершин которого V₁  V, а множество ребер Е₁ содержит все ребра графа G, инцидентные выбранным вершинам V₁.

Например: