Теорема Эйлера для плоского графа.

Для любого связного графа G, являющегося плоским справедливо соотношение:p–q+f= 2, гдеpколичество вершин,qколичество ребер,fколичество граней плоского графа.

.

Пример:

p = 4

q = 4 4 – 4 + 2 = 2

f = 2

p = 4

q = 6 4 – 6 + 4 = 2

f = 4

p = 7

q = 6 7 – 6 + 1 = 2

f = 1

Критерии планарности

Критерий Понтрягина-Куратовского (критерий планарности). Граф планарен тогда, когда он не содержит подграфов гомеоморфных K₅ или K_3,3.

Критерий Вагнера. Граф планарен тогда, когда он не содержит подграфов, стягиваемых K₅ или K_3,3 (по методу операции стягивания).

Примеры: Граф Петерсена

Граф G1 – не планарен, т. к. он содержит подграф G2, гомеоморфный K_3,3

Алгоритм плоской укладки графа

Алгоритм  графа G представляет собой процесс последовательного присоединения к некоторому уже уложенному графу (подграф графа G) некоторой новой цепи также принадлежащей G оба конца которой принадлежат . Эта цепь разбивает одну из граней графа на две. При этом в качестве начального плоского графа выбирается любой простой цикл исходного графа. Процесс продолжается до тех пор, пока не будет получена плоская укладка графа G или присоединение некоторой цепи оказывается невозможным, в том случае граф является не планарным.

Пусть есть граф G и пусть построена некоторая плоская укладка подграфа графа G, тогда сегментом S относительно G будем называть подграф исходного графа G одного из следующих двух видов:

1. ребра e = uv исходного графа G такие, что e  плоской укладке, но вершины uv уже есть в плоской укладке.

2. связная компонента графа G - дополненной всеми ребрами графа G, инцидентными вершинам взятой компоненты и концевыми вершинами этих ребер.

Г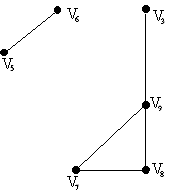рафG - (вычтем граф из исходного графа G)

Контактная вершина  это вершина v сегмента S относительно , если она принадлежит множеству вершин очередной плоской укладки.

Допустимой гранью для сегмента S называется грань Г графа , которая содержит все контактные вершины сегмента S.

Обозначим Г (Si)  множество всех допустимых граней для сегмента Si.

Простая цепь  сегмента S, содержащая 2 различные контактные вершины и не содержащая других контактных вершин, называется -цепью.

Простая -цепь проходит из контактной через неконтактные и возвращается в контактную вершину.

Алгоритм .

0. Выберем некоторый простой цикл C графа G и уложим его на плоскости (лучше выбирать окружение).

1. Найдем грани графа и множество сегментов S относительно . Если множество сегментов пусто перейти к п. 7.

2. Для каждого сегмента S найдем множество допустимых граней Г (S).

3. Если существует сегмент S для которого Г (S) =  (множество граней пусто), то граф G не планарен. Выход из алгоритма, иначе переход к п. 4.

4. Если существует сегмент S для которого ровно одна допустимая грань (|Г(S)| = 1), то перейдем к п. 6, иначе п. 5.

5. Для некоторого сегмента S выбираем произвольную допустимую грань Г.

6. Поместим произвольную -цепь L, принадлежащую S, в грань Г, заменим на L и перейдем к п. 1.

7. Построена плоская укладка графаG. Шагом алгоритма считается присоединение к опр. -цепи.

Пример:

Г(S1) = Г(S2) = Г(S3) = {Г1, Г2}

S2: -цепь = {4, 5, 2} в Г2

Г(S1) = {Г1, Г2, Г3}, Г(S2) = {Г2}, Г(S3) = {Г1, Г3}

S2:-цепь = {1, 5,} в Г2

Г(S1) = {Г1, Г3}, Г(S3) = {Г1, Г3}

S1:-цепь = {2, 4,} в Г3

Г(S3) = {Г1, Г5}

S3:  цепь: {2, 6, 3} в Г1

Г(S) = {Г1}

S: -цепь = {4, 6} в Г1