Комплексный пример основных расчетов по работе 3
1.Исходный массив 15 наблюдений расположен в ячейкахB3:E17(табл.3.6).
Таблица 3.6 – Исходные данные и массив стандартизованных объясняющих переменных
|
|
A |
B |
C |
D |
E |
F |
G |
H |
|
1 |
|
|
|
|
|
|
|
|
|
2 |
Набл-ние |
Y |
X1 |
X2 |
X3 |
Х1* |
Х2* |
Х3* |
|
3 |
1 |
21,6 |
25,2 |
25,8 |
7,9 |
1,407477 |
-1,92156 |
-1,59927 |
|
4 |
2 |
25,2 |
24,3 |
31,3 |
8,1 |
1,263312 |
-1,44 |
-1,56317 |
|
5 |
3 |
26,0 |
23,9 |
36,4 |
9,5 |
1,199239 |
-0,99347 |
-1,31047 |
|
6 |
4 |
36,4 |
22,6 |
38,7 |
10,3 |
0,991001 |
-0,79209 |
-1,16606 |
|
7 |
5 |
38,5 |
21,5 |
39,1 |
13,1 |
0,814799 |
-0,75707 |
-0,66065 |
|
8 |
6 |
43,6 |
20,4 |
45,3 |
15,5 |
0,638597 |
-0,21422 |
-0,22744 |
|
9 |
7 |
40,1 |
19,1 |
45,4 |
17,0 |
0,430359 |
-0,20546 |
0,043321 |
|
10 |
8 |
47,8 |
14,7 |
52,0 |
17,0 |
-0,27445 |
0,372405 |
0,043321 |
|
11 |
9 |
55,5 |
14,4 |
47,3 |
19,6 |
-0,3225 |
-0,03911 |
0,512634 |
|
12 |
10 |
59,8 |
14,0 |
51,8 |
20,8 |
-0,38658 |
0,354894 |
0,72924 |
|
13 |
11 |
68,0 |
12,2 |
55,9 |
20,7 |
-0,67491 |
0,713873 |
0,71119 |
|
14 |
12 |
69,5 |
11,8 |
58,9 |
21,6 |
-0,73898 |
0,976542 |
0,873644 |
|
15 |
13 |
73,4 |
8,9 |
61,0 |
23,4 |
-1,20351 |
1,160409 |
1,198553 |
|
16 |
14 |
72,2 |
7,3 |
64,2 |
23,0 |
-1,4598 |
1,440588 |
1,126351 |
|
17 |
15 |
76,6 |
5,9 |
63,1 |
23,9 |
-1,68406 |
1,344277 |
1,288806 |
|
18 |
Ср.знач. |
|
16,41333 |
47,74667 |
16,76 |
0 |
-4,4E-15 |
-5,1E-15 |
|
19 |
Ст.откл. |
|
6,242848 |
11,42126 |
5,540012 |
|
|
|
|
20 |
n= |
15 |
|
|
|
|
|
|
|
21 |
m= |
3 |
|
|
|
|
|
|
1.1.По исходным
данным, расположенным в блокеB3:E17,
с помощью инструментаАнализ
Данных/Регрессияпостроена множественная
линейная регрессияYна факторы
.
Полученные таблицы регрессионного
анализа представлены в табл.3.7.
Проанализируем статистическое качество исходной эконометрической модели.
Коэффициент детерминации 0,968117(значение высокое) указывает на весьма высокую степень обусловленности вариации результата вариацией включенных в модель факторов (96,81%), иными словами – на очень тесную связь факторов и результата.
Уровень значимости F-статистики1,64E-08значительно меньше допустимого уровня значимости 0,05. Поэтому с надежностью 0,95 полученное значение коэффициента детерминации не случайно, оно сформировалось под влиянием существенных факторов. Следовательно, модель в целом является статистически достоверной.
Знаки оценок параметров модели не противоречат теории:
средний эффект всех факторов, которые влияют на объем спроса, за исключением включенных в модель, не отрицательный
;с увеличением цены товара объем спроса на него снижается
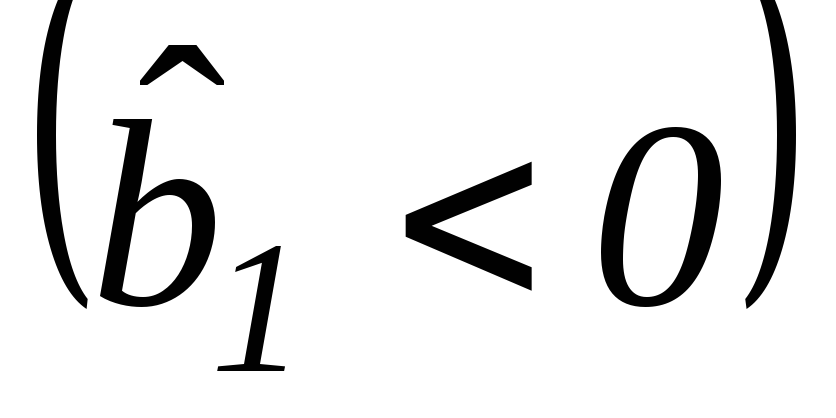;спрос на товар растет, если растут цены на его товары-заменители
.
Таблица 3.7 – Регрессия по исходным данным
|
ВЫВОД ИТОГОВ |
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
Регрессионная статистика |
|
|
|
|
| |
|
Множественный R |
0,983929 |
|
|
|
|
|
|
R-квадрат |
0,968117 |
|
|
|
|
|
|
Нормированный R-квадрат |
0,959422 |
|
|
|
|
|
|
Стандартная ошибка |
3,820525 |
|
|
|
|
|
|
Наблюдения |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ |
|
|
|
| ||
|
|
df |
SS |
MS |
F |
Значимость F |
|
|
Регрессия |
3 |
4875,384 |
1625,128 |
111,3375 |
1,64E-08 |
|
|
Остаток |
11 |
160,5605 |
14,59641 |
|
|
|
|
Итого |
14 |
5035,944 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
Нижние 95% |
Верхние 95% |
|
Y-пересечение |
35,0286 |
28,698 |
1,220594 |
0,247759 |
-28,1353 |
98,19251 |
|
X1 |
-1,25535 |
0,720522 |
-1,74227 |
0,109311 |
-2,8412 |
0,330514 |
|
X2 |
0,333936 |
0,390887 |
0,854302 |
0,411157 |
-0,5264 |
1,194273 |
|
X3 |
1,188036 |
0,747852 |
1,588599 |
0,140458 |
-0,45798 |
2,834047 |
Р-значения оценок параметров:
для
(Y-пересечение):0,247759>
0,05;
для
(коэффициент приX1): 0,109311>
0,05;
для
(коэффициент приX2): 0,411157>
0,05;
для
(коэффициент приХ3): 0,140458>
0,05.
Следовательно, с надежностью 0,95 оценки всех параметров статистически не значимы, что позволяет рассматривать все факторы какнеинформативныеи ставить под сомнение необходимость включения их в модель.
Возникшее противоречие (F-критерий утверждает достоверность модели в целом, а t‑критерий – недостоверность оценок параметров) обычно определяется существующей между объясняющими переменными мультиколлинеарностью. Поэтому целесообразно выполнить исследование массива объясняющих переменных на мультиколлинеарность по методу Фаррара-Глобера.
1.2.Для построения по исходным данным, расположенным в блокеB3:E17, общей корреляционной матрицы выбираемСервис/Анализ данных/Корреляцияи в диалоговом окне указываем:
Входной интервал$B$2:$E$17
Группированиепо столбцам
Метки в первой строке
Выходной интервал$A$45
Подтверждаем ОК.
В результате в ячейках A45:E49появитсянижний треугольниккорреляционной матрицы (см. табл.3.8).
Следует заметить,
что знаки полученных в ячейках B47:B49коэффициентов корреляции между зависимой
переменнойYи объясняющими переменными
,
совпадают со знаками оценок параметров
множественной линейной регрессии,
которые были получены ранее (см. в
табл.3.7 колонку«Коэффициенты»).
Таблица 3.8 – Корреляционная матрица объясняющих переменных
|
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
|
44 |
Общая корреляционная матрица |
|
|
|
|
| |||
|
45 |
|
Y |
X1 |
X2 |
X3 |
Корр.матрица КОРРЕЛЯЦИЯ |
| ||
|
46 |
Y |
1 |
|
|
|
|
X1 |
X2 |
X3 |
|
47 |
X1 |
-0,97569 |
1 |
|
|
X1 |
1 |
|
|
|
48 |
X2 |
0,968695 |
-0,96905 |
1 |
|
X2 |
-0,96905 |
1 |
|
|
49 |
X3 |
0,972048 |
-0,96397 |
0,963418 |
1 |
X3 |
-0,96397 |
0,963418 |
1 |
|
50 |
|
|
|
|
|
|
|
|
|
|
51 |
|
Корр.матрица по стандартиз.перем. |
Достроенная корр.матрица |
| |||||
|
52 |
|
|
|
|
|
|
X1 |
X2 |
X3 |
|
53 |
|
1 |
-0,96905 |
-0,96397 |
|
X1 |
1 |
-0,96905 |
-0,96397 |
|
54 |
|
-0,96905 |
1 |
0,963418 |
|
X2 |
-0,96905 |
1 |
0,963418 |
|
55 |
|
-0,96397 |
0,963418 |
1 |
|
X3 |
-0,96397 |
0,963418 |
1 |
2.Находимкорреляционную матрицуrобъясняющих переменных.