
- •Розділ 1. Лінійна регресія
- •Проста лінійна регресія
- •Опис моделі
- •Знаходження оцінок параметрів регресії методом найменших квадратів
- •Рівняння вибіркої регресії приймає вигляд
- •1.1.3.Властивості залишків методу найменших квадратів
- •1.1.4.Розклад дисперсії залежної змінної. Коефіціент детермінації
- •1.1.5.Статистичні властивості оцінок методу найменших квадратів
- •1.1.6.Статистичні висновки в моделі простої лінійної регресії Перевірка гіпотез про коефіцієнт нахилу регресії
- •Інтервальне оцінювання
- •Перевірка значущості регресії
- •1.1.7. Прогнозування за допомогою простої лінійної регресії
- •1.1.8.Приклад
Розділ 1. Лінійна регресія
Проста лінійна регресія
Опис моделі
Припустимо, що існують дві змінні x i y, де x - незалежна змінна (регресор), y - залежна змінна. Співвідношення між цими змінними позначимо: y = f (x). Будемо розрізняти детерміновані і статистичні співвідношення. При статистичному співвідношенні кожному значенню x відповідає не єдине значення y, але залежну змінну y можливо точно описати у імовірнісних термінах. Припустимо, що функція f(x) лінійна за x, тобто f(x) = + x, а співвідношення між x та y є статистичним, а саме
y = + x + , (1.1)
де доданок називається збуренням або похибкою і має відомий імовірносний розподіл (тобто є випадковою величиною). В рівнянні (1.1) + x є детермінованим компонентом, збурення є випадковим або стохастичним компонентом; і називаються регресійними коефіцієнтами або параметрами регресії, які потрібно оцінити на основі даних про x та y.
Нехай
ми маємо n
пар значень
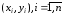 .
Кожну пару будемо називатиспостереженням.
Ми
можемо записати рівняння (1.1) у вигляді
.
Кожну пару будемо називатиспостереженням.
Ми
можемо записати рівняння (1.1) у вигляді
yi = + xi + (1.2)

Наша мета - знайти оцінки невідомих параметрів та в рівнянні (1.2) на основі n спостережень x та y. Щоб це зробити ми повинні накласти деякі умови щодо збурень i.
Нульове середнє: Ei = 0,
 .
.
Рівність дисперсій (гомоскедастичність): Di = E
 =2
= const,
=2
= const, .
.Незалежність збурень: і та j незалежні при
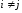 .
Зокрема,
cov(i,
j
) = Eij
= 0 при
.
Зокрема,
cov(i,
j
) = Eij
= 0 при
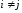 .
.Незалежність збурень та регресора: xi та j незалежні для всіх i та j. Якщо xi вважаються невипадковими, то дане припущення виконано автоматично.
В деяких випадках будемо накладати додаткове припущення (ми будемо вказувати в тексті, для виконнання яких результатів воно необхідно):
Нормальність. Збурення i нормально розподілені для всіх i. Взявши до уваги припущення 1-3, ми можемо сказати, що i – незалежні нормально розподілені випадкові величини з нульовим математичним сподіванням і однаковими дисперсіями 2, або
 .
.
Отже, модель простої лінійної регресії описується за допомогою рівнянь (1.2), збурення в яких задовольняють припущенням 1 – 5.
Оскільки
Ei
= 0, то з рівняння (1.2) маємо E(yi)
=

+ xi
. Останній вираз називається популяційною
функцією регресії.
Таким чином, популяційна функція регресії
– функція умовного математичного
сподівання. Якщо замінити значення
параметрів їх оцінками, одержимо
вибіркову
функцію регресії.
Популяційна регресійна функція дає
усереднене, або закономірне значення
незалежної змінної, яке відповідає
даному значенню незалежної змінної.
Збурення можна інтерпретувати як
відмінність поведінки залежної змінної
від усередненої в кожній конкретній
ситуації.
+ xi
. Останній вираз називається популяційною
функцією регресії.
Таким чином, популяційна функція регресії
– функція умовного математичного
сподівання. Якщо замінити значення
параметрів їх оцінками, одержимо
вибіркову
функцію регресії.
Популяційна регресійна функція дає
усереднене, або закономірне значення
незалежної змінної, яке відповідає
даному значенню незалежної змінної.
Збурення можна інтерпретувати як
відмінність поведінки залежної змінної
від усередненої в кожній конкретній
ситуації.
Друге припущення означає,що для кожного спостереження дія випадкових факторів в середньому однакова .
Третє припущення означає, що для кожного спостереження випадкові фактори діють незалежно.
Знаходження оцінок параметрів регресії методом найменших квадратів
Нехай
 та
та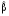 –деякі
оцінки параметрів
та .
Запишемо рівняння вибіркової регресії
–деякі
оцінки параметрів
та .
Запишемо рівняння вибіркової регресії
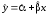 .
Тоді
.
Тоді є оцінкоюEyi,
побудованою на основі вибіркової
регресії. Позначимо через
є оцінкоюEyi,
побудованою на основі вибіркової
регресії. Позначимо через
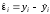 різницю
між значенням y,
яке спостерігалось, і обчисленим з
регресії. Оцінки методу
найменших квадратів
(скорочено – МНК-оцінки)
знаходяться з умови мінімізаціїї за
всіма можливими значеннями
різницю
між значенням y,
яке спостерігалось, і обчисленим з
регресії. Оцінки методу
найменших квадратів
(скорочено – МНК-оцінки)
знаходяться з умови мінімізаціїї за
всіма можливими значеннями
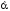 та
та виразу
виразу
 . (1.3)
. (1.3)
Позначимо
на координатній площині точки
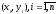 і побудуємо графіки прямих
і побудуємо графіки прямих
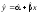 для різних значень
для різних значень і
і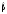 .
Знаходження оцінок методом найменших
квадрвтів означає пошук прямої, яка
знаходиться найближче до даних точок
у тому розумінні, що сума квадратів
відстаней по вертикалі від даних точок
до прямої буде найменшою. Обгрунтування
такого вибору методу побудови оцінок
полягає в їх оптимальних статистичних
властивостях, які сформульовано вище.
.
Знаходження оцінок методом найменших
квадрвтів означає пошук прямої, яка
знаходиться найближче до даних точок
у тому розумінні, що сума квадратів
відстаней по вертикалі від даних точок
до прямої буде найменшою. Обгрунтування
такого вибору методу побудови оцінок
полягає в їх оптимальних статистичних
властивостях, які сформульовано вище.
Щоб
мінімізувати вираз (1.3), запишемо необхідну
умову екстремуму, тобто прирівняємо
похідні відносно
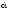 та
та до
нуля. Маємо
до
нуля. Маємо
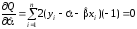 ,
,
звідки
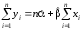 (1.4)
(1.4)
і
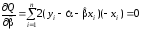 ,
,
звідки
 . (1.5)
. (1.5)
Система рівнянь (1.4) і (1.5) називається системою нормальних рівнянь.
Уведемо такі позначення:
 ,
,
 ,
, ,
,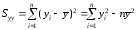 ,
, .
.
Нехай
Sxx
>
0. Запишемо
розв’язок
системи нормальних рівнянь відносно
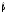 за правилом Крамера:
за правилом Крамера:
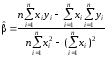 (1.6).
(1.6).
Розділимо чисельник
і знаменник виразу (1.6) на n.
Враховуючи уведені позначення, остаточно
одержимо:
 .
Розділимо перше нормальне рівняння
(1.4) почленно на n.
Маємо:
.
Розділимо перше нормальне рівняння
(1.4) почленно на n.
Маємо: .
Надалі будемо позначати МНК-оцінки
параметрів
та
латинськими літерами a
та
b.
Отже, МНК-оцінки параметрів моделі
простої лінійної регресії знаходяться
за фомулами:
.
Надалі будемо позначати МНК-оцінки
параметрів
та
латинськими літерами a
та
b.
Отже, МНК-оцінки параметрів моделі
простої лінійної регресії знаходяться
за фомулами:
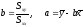 . (1.7)
. (1.7)
Якщо обчислити матрицю других похідних для Q, то можна побачити, що ця матриця додатньо визначена, отже значення (1.7) дійсно мінімізують (1.3).
