1.1.5.Статистичні властивості оцінок методу найменших квадратів

Оцінки методу найменших квадратів є незміщеними¹⁾:

Eb = , Ea =  .

Дисперсії та коваріація оцінок методу найменших квадратів обчислюються за наступними формулами:

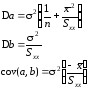. (1.18)

Наведені формули не можна використовувати для перевірки гіпотез та інтервального оцінювання, оскільки до них входить невідомий параметр – дисперсія збурень ² . Отже, нам потрібно вміти знаходити її оцінку. Має місце наступний результат: статистика

є незміщеною оцінкою ². Якщо збурення нормально розподілені, то a та b також нормально розподілені. Величина

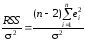
має ² - розподіл з n - 2 ступенями свободи. Більше того, випадкова величина RSS не залежить від a та b.

Далі ми будемо припускати, що збурення нормально розподілені. Як відомо, якщо випадкові величини ₁~N(0,1), ₂~незалежні²⁾, то

має розподіл Стьюдента з p ступенями свободи.

Оскільки 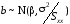, то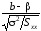має стандартний нормальний розподіл. Крім того,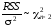і ці випадкові величини незалежні. Отже, частка

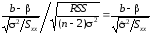
має розподіл Стьюдента з n - 2 ступенями свободи. Величина є оцінкою дисперсіїb, а 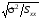– оцінкою середньоквадратичного відхилення, або, коротко,стандартною похибкою оцінки b. Уведемо позначення SE(b) = 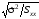(від англійськогоstandard error - стандартна похибка). Маємо

(1.19)

1.1.6.Статистичні висновки в моделі простої лінійної регресії Перевірка гіпотез про коефіцієнт нахилу регресії

Стандартною процедурою є перевірка гіпотези про те, що коефіцієнт нахилу регресійної прямої  дорівнює нулю. Прийняття цієї гіпотези означає, що незалежна змінна не має впливу на залежну в рамках лінійної моделі. Не виключено, що насправді між змінними існує залежність, але виражена іншою функціональною формою. Статистика для перевірки гіпотези має вигляд

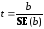(1.20)

Значення цієї t-статистики, як правило, автоматично підрахо-вуються в комп’ютерних програмах з регресійного аналізу. Для перевірки гіпотези H₀:  = ₀ використовують наступну статистику

(1.21)

За вибраним рівнем значущості  в таблиці розподілу Стьюдента з n-2 ступенями свободи знаходимо критичне значення t_кр. Якщо t < t_кр, то гіпотеза H₀ приймається. Якщо t  t_кр, то гіпотеза H₀ відхиляється.

Інтервальне оцінювання

Інтервальна оцінка параметра  з рівнем довіри 1- (не плутати з постійним доданком у регресії) знаходиться за наступною формулою:

, (1.22)

де значення t_кр знаходиться за вибраним  в таблиці розподілу Стьюдента з n-2 ступенями свободи.

Перевірка значущості регресії

Значущість регресії означає, що незалежні змінні впливають на залежну змінну. Для простої лінійної регресіі це еквівалентно тому, що коефіцієнт нахилу не дорівнює нулю (тобто коли гіпотеза про рівність  нулю відхиляється) . Якщо b = 0, то 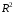= 0. Тому логічно будувати критерій, який грунтується на значенні коефіцієнта детермінації. Дійсно, можна показати, що

, (1.23)

коли  = 0, де через F_1,n–2 позначено розподіл Фішера з 1, n–2 ступенями свободи. За вибраним рівнем значущості  в таблиці розподілу Фішера з 1, n-2 ступенями свободи знаходимо критичне значення F _кр. Якщо F<F_кр, то гіпотеза приймається. Якщо FF_кр, то гіпотеза відхиляється. У випадку простої регресії застосування F-критерія (1.23) не дає нової інформації порівняно з t-критерієм (1.20), оскільки і. Але це не так у випадку множинної регресії, що ми побачимо пізніше.