- •1. Множественная линейная регрессия Задание
- •Методические рекомендации по выполнению работы
- •Комплексный пример основных расчетов по работе
- •2. Мультиколлинеарность Задание
- •Методические рекомендации по выполнению работы
- •2.1. Способ 1.
- •2.2. Способ 2.
- •6.1. Способ 1.
- •6.2. Способ 2.
- •Комплексный пример основных расчетов по работе 3
- •2.1. Способ 1.
- •2.2. Способ 2.
- •6.1. Способ 1.
- •6.2. Способ 2.
- •3. Гетероскедастичность Задание
- •Методические рекомендации по выполнению работы
- •4. Автокорреляция остатков Задание
- •Методические рекомендации по выполнению работы
Методические рекомендации по выполнению работы
1.Исходные данные заносим в таблицу, аналогичную табл.2.5. При этом следует обратить внимание на то, что варианты исходных данных отличаются не только числовыми значениями, но и разным количеством наблюдений. Число исходных факторов тоже разное – в одних вариантах 2 фактора, в других вариантах – 3 фактора.
Вычисляем средние значения исходных переменных, их дисперсии и среднеквадратические (стандартные) отклонения. Затем входные данные переменных стандартизуем по формулам (2.3).
Обратите также
внимание, что в табл.2.5 дополнительно
должен быть введен фиктивный фактор
![]() ,
все значения которого равны 1 (это
потребуется в дальнейшем).
,
все значения которого равны 1 (это
потребуется в дальнейшем).
Таблица 2.5 – Исходные данные в естественном и стандартизованном масштабах, когда рассматривается два исходных фактора
|
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
|
1 |
Наблюде-ние |
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
5 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
6 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
7 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
9 |
8 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
9 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
10 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
11 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
13 |
Сума значений |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
14 |
Среднее знач. |
|
- |
|
|
- |
- |
- |
|
|
|
0 |
0 |
0 |
|
15 |
Ср.кв. отклон. |
- |
- |
- |
- |
- |
- |
- |
|
|
|
- |
- |
- |
|
16 |
Вектор
прогноз. значений факторов |
- |
1 |
… |
… |
- |
- |
- |
- |
- |
- |
- |
- |
- |
2.Находим
корреляционную матрицу![]() .
.
Способ 1.
Элементы
![]() ,
,![]() матрицы
матрицы![]() можно вычислить с помощью встроенной
статистической функцииКОРРЕЛпакета MSExcel. Например,
при расположении данных как в табл.2.5,
значение
можно вычислить с помощью встроенной
статистической функцииКОРРЕЛпакета MSExcel. Например,
при расположении данных как в табл.2.5,
значение![]() вычислим, введя формулу:=КОРРЕЛ(L2:L12;M2:M12)
вычислим, введя формулу:=КОРРЕЛ(L2:L12;M2:M12)
Значение
![]() вычислим, введя формулу:=КОРРЕЛ(L2:L12;N2:N12)
вычислим, введя формулу:=КОРРЕЛ(L2:L12;N2:N12)
Значение
![]() вычислим, введя формулу:=КОРРЕЛ(M2:M12;N2:N12)
вычислим, введя формулу:=КОРРЕЛ(M2:M12;N2:N12)
Способ 2.
Матрицу
![]() можно вычислить с помощью инструментаАнализа Данных «Корреляция»пакета
MSExcel, выполнив следующие
действия:
можно вычислить с помощью инструментаАнализа Данных «Корреляция»пакета
MSExcel, выполнив следующие
действия:
в главном меню выберите Сервис/Анализ данных/Корреляция. Щелкните по кнопкеОК;
заполните диалоговое окно Входные данныеиПараметры вывода:
Входной интервал– ссылка на диапазон, содержащий анализируемые данные результативного признака и факторов (в табл.2.5 – это:L2:N12– сами данные;L1:N12– данные с названиями столбцов в первой строке). Ссылка должна состоять не менее чем из двухсмежныхдиапазонов данных, данные в которых расположены по строкам или по столбцам;
Группирование– флажок, который указывает, как расположены данные во входном диапазоне –по столбцамилипо строкам;
Метки в первой строке/Метки в первом столбце–флажок,который указывает, содержит ли первая строка (столбец) входного диапазона название столбцов (строк) или нет. Если входной диапазон не содержит меток, то необходимые заголовки в выходном диапазоне будут созданы автоматически;
Выходной интервал– достаточно указать ссылку на левую верхнюю ячейку выходного диапазона. Поскольку коэффициент корреляции двух наборов данных не зависит от последовательности их обработки, товыходная область занимает только половину предназначенного для нее места(корреляционная матрица симметрична относительно главной диагонали). Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждая строка или столбец во входном диапазоне полностью коррелирует с самим собой;
Новый рабочий лист– можно задать произвольное имя нового листа.
Щелкните по кнопке ОК.
Корреляционная матрица при установленном флажке Метки в первой строкевыглядит следующим образом (пример):
Таблица 2.6 – Пример корреляционной матрицы
|
|
Y* |
X1* |
X2* |
|
Y* |
1 |
|
|
|
X1* |
0,904189 |
1 |
|
|
X2* |
0,479175 |
0,476585 |
1 |
Находим
![]() .
.
Пример.
В табл.2.6
![]() =0,904189,т.е. максимальное
=0,904189,т.е. максимальное![]() указывает на объясняющую переменную
указывает на объясняющую переменную![]() ,
которая теснее всего связана сY.
Тогда методом наименьших квадратов
находим оценку параметра модели
,
которая теснее всего связана сY.
Тогда методом наименьших квадратов
находим оценку параметра модели![]() :
выделяем блок пустых ячеек, состоящий
из двух столбцов и пяти строк, и вводим
формулу
:
выделяем блок пустых ячеек, состоящий
из двух столбцов и пяти строк, и вводим
формулу
=ЛИНЕЙН(L2:L12;M2:M12;0;1)
Нажимаем клавишу F2, затем – клавишиCtrl+Shift+Enter. В результате получаем таблицу регрессионной статистики:
|
0,904189 |
0 |
|
0,135071 |
#Н/Д |
|
0,817558 |
0,447981 |
|
44,81184 |
10 |
|
8,993134 |
2,006866 |
Следовательно,
![]() =0,904189.
=0,904189.
Вычисляем
остатки
![]() ,
где
,
где![]() – стандартизованные наблюдаемые
значения объясняемой переменной, которые
в табл.2.5 расположены в ячейкахL2:L12;
– стандартизованные наблюдаемые
значения объясняемой переменной, которые
в табл.2.5 расположены в ячейкахL2:L12;![]() – прогнозные (расчетные) стандартизованные
значения объясняемой переменной, которые
необходимо рассчитать по уравнению
– прогнозные (расчетные) стандартизованные
значения объясняемой переменной, которые
необходимо рассчитать по уравнению![]() принаблюдаемыхстандартизованных
значениях объясняющей переменной
принаблюдаемыхстандартизованных
значениях объясняющей переменной![]() .
Затем рассчитываем сумму квадратов
остатков
.
Затем рассчитываем сумму квадратов
остатков![]() .
.
Результаты удобно представить в форме табл.2.7.
Поскольку в табл.2.5 в ячейках L2:N12содержатся формулы, то при копировании вычисленных по этим формулам стандартизованных значений переменных из табл.2.5 в табл.2.7 необходимо:
выделить ячейки L2:N12;
находясь указателем в выделенной зоне нажать правую кнопку мыши и выбрать Копировать;
переместить указатель в левую верхнюю ячейку месторасположения данных табл.2.7;
нажать правую кнопку мыши, выбрать Специальная вставка…, в диалоговом окнеВставитьустановить флажокзначенияи щелкнуть по кнопкеОК.
Таблица 2.7 – Данные для расчета стандартизованных остатков
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
… |
|
|
|
|
|
|
|
|
|
|
… |
… |
… |
|
|
|
|
|
|
|
|
|
|
… |
… |
… |
|
|
|
|
|
|
|
|
|
|
∑ |
- |
- |
- |
- |
|
- |
- |
|
- |
- |
|
После этого
среди тех значений
![]() ,
которые остались, выбираем
,
которые остались, выбираем![]() и в модель вводим следующую объясняющую
переменную. Если, например, максимальным
окажется
и в модель вводим следующую объясняющую
переменную. Если, например, максимальным
окажется![]() ,
указывающее на объясняющую переменную
,
указывающее на объясняющую переменную![]() ,
то строим эконометрическую модель
,
то строим эконометрическую модель
![]() .
.
Методом наименьших
квадратов (с помощью встроенной
статистической функции ЛИНЕЙН)
находим оценки параметров модели![]() ,
рассчитывает остатки
,
рассчитывает остатки![]() и сумму квадратов остатков
и сумму квадратов остатков![]() .
.
С учетом того,
что в первой модели один фактор
![]() ,
а во вторую модель добавлен только один
новый фактор, находим расчетное значениеF-статистики:
,
а во вторую модель добавлен только один
новый фактор, находим расчетное значениеF-статистики:
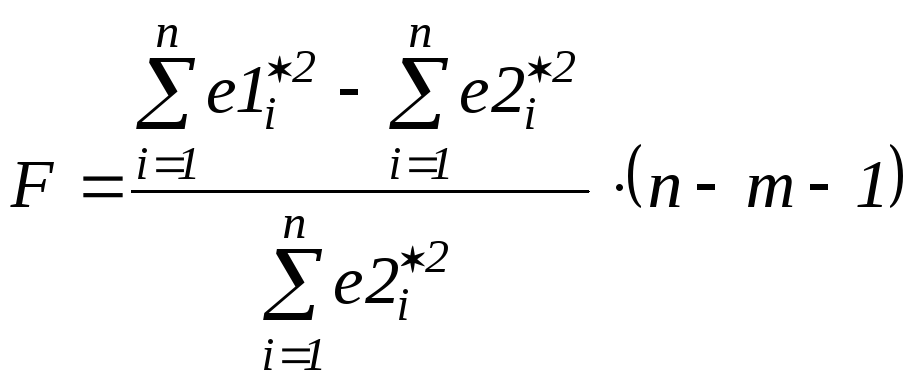 =
= .
.
Для уровня
значимости
![]() и степеней свободы
и степеней свободы![]() ,
,![]() по табл.2.8 находим табличное значениеF-статистики
по табл.2.8 находим табличное значениеF-статистики![]() .
.
Таблица 2.8
– Таблица F-распределения
Фишера (![]() - степени свободы,
- степени свободы,![]() )
)
|
|
1 |
2 |
3 |
4 |
… |
|
1 |
161,4 |
199,5 |
215,7 |
224,6 |
… |
|
2 |
18,51 |
19,00 |
19,16 |
19,25 |
… |
|
3 |
10,13 |
9,55 |
9,28 |
9,10 |
… |
|
4 |
7,71 |
6,94 |
6,59 |
6,39 |
… |
|
5 |
6,61 |
5,79 |
5,41 |
5,19 |
… |
|
6 |
5,99 |
5,14 |
4,76 |
4,53 |
… |
|
7 |
5,59 |
4,74 |
4,35 |
4,12 |
… |
|
8 |
5,32 |
4,46 |
4,07 |
3,84 |
… |
|
9 |
5,12 |
4,26 |
3,86 |
3,63 |
… |
|
10 |
4,96 |
4,10 |
3,71 |
3,48 |
… |
|
11 |
4,84 |
3,98 |
3,59 |
3,36 |
… |
|
12 |
4,75 |
3,89 |
3,49 |
3,26 |
… |
|
13 |
4,67 |
3,81 |
3,41 |
3,18 |
… |
|
14 |
4,60 |
3,74 |
3,34 |
3,11 |
… |
|
15 |
4,54 |
3,68 |
3,29 |
3,06 |
… |
|
16 |
4,49 |
3,63 |
3,24 |
3,01 |
… |
|
17 |
4,45 |
3,59 |
3,20 |
2,96 |
… |
|
18 |
4,41 |
3,55 |
3,16 |
2,93 |
… |
|
… |
… |
… |
… |
… |
… |
Если
![]() ,
то с заданной надежностью
,
то с заданной надежностью![]() можно считать, что новый факторнесущественновлияет на показательYи его необходимо исключить из модели.
Тогда рациональным следует считать
первый вариант модели:
можно считать, что новый факторнесущественновлияет на показательYи его необходимо исключить из модели.
Тогда рациональным следует считать
первый вариант модели:![]() .
.
Если окажется,
что
![]() ,
то с заданной надежностью
,
то с заданной надежностью![]() можно считать, что новый фактор существенно
влияет на показательY,
и его необходимовключитьв модель.
можно считать, что новый фактор существенно
влияет на показательY,
и его необходимовключитьв модель.
При наличии
следующего фактора цикл повторяется.
При этом в модель
![]() включается третий фактор, оцениваются
параметры уравнения регрессии с тремя
факторами, рассчитываются остатки и
сумма квадратов остатков, а при оценке
обоснованности включения третьего
фактора учитываем, что теперь
включается третий фактор, оцениваются
параметры уравнения регрессии с тремя
факторами, рассчитываются остатки и
сумма квадратов остатков, а при оценке
обоснованности включения третьего
фактора учитываем, что теперь![]() .
.
3.Пересчет стандартизованных оценок параметровокончательного вариантапостроенной модели в естественный масштаб выполняется по формулам (2.6).
Записываем оцененное уравнение регрессии в естественном масштабе.
4.С помощью инструментаАнализ Данных/Регрессияпакета MSExcelвыполняется построение и анализ статистического качества линейной эконометрической модели вестественном масштабе, включающей только отобранные ранее пошаговым регрессионным методом наиболее существенные факторы.
В отчете необходимо:
привести результаты регрессионного анализа, полученные с помощью инструмента Анализа Данных/Регрессия;
описать содержимое таблиц результатов;
проанализировать результаты, сравнить их с результатами, полученными ранее (см. п.3).
привести графики изменения остатков регрессии для каждого включенного в модель фактора.
5.При изучении
тенденций развития исследуемого
экономического объекта (процесса,
явления) множественную линейную модель
используют для полученияпрогнозных
значенийобъясняемой переменнойYот некоторого набора предполагаемых
значений отобранных ранее наиболее
информативных факторов![]() .
.
Точечный прогнозпоказателяYполучим подстановкой прогнозных значений отобранных факторов (см. п.5 последовательности выполнения задания) в полученное уравнение эконометрической модели в естественном масштабе.
6.Поскольку
на процесс построения модели существенно
влияет объем наблюдений, необходимо
использовать не только точечную оценку
прогноза![]() ,
но и найти доверительные интервал для
истинного значения прогноза (интервальный
прогноз).
,
но и найти доверительные интервал для
истинного значения прогноза (интервальный
прогноз).
С надежностью
![]() доверительный интервалдля
математического ожидания прогноза
показателяY:
доверительный интервалдля
математического ожидания прогноза
показателяY:
![]() ,
,
где
![]() ;
;
![]() -
критическое значениеt-распределения
Стьюдента приn-m-1степенях свободы и уровне значимости
-
критическое значениеt-распределения
Стьюдента приn-m-1степенях свободы и уровне значимости![]() ;
;
![]() -
оценка стандартной ошибки оценивания
(приводится в результатах регрессионного
анализа, полученных ранее с помощью
инструментаАнализа Данных «Регрессия»пакетаMSExcel);
-
оценка стандартной ошибки оценивания
(приводится в результатах регрессионного
анализа, полученных ранее с помощью
инструментаАнализа Данных «Регрессия»пакетаMSExcel);
![]() -
скорректированная оценка дисперсии
ошибок модели;
-
скорректированная оценка дисперсии
ошибок модели;
![]() -
матрица исходных(наблюдаемых)значений наиболее информативных
объясняющих переменных размерности
-
матрица исходных(наблюдаемых)значений наиболее информативных
объясняющих переменных размерности![]() :
:
 .
.
В этой матрице
каждая строка представляет наблюдение
вектора значений объясняющих переменных;
единицасоответствует фиктивной
переменной при свободном члене![]() ;
;
![]() -
транспонированная матрица размерности
-
транспонированная матрица размерности![]() по отношению к матрицеХ;
по отношению к матрицеХ;
![]() -
обратная матрица размерности
-
обратная матрица размерности![]() по отношению к произведению матриц
по отношению к произведению матриц![]() ;
;
![]() -
вектор-столбец прогнозных значений
наиболее информативных объясняющих
переменных размерности
-
вектор-столбец прогнозных значений
наиболее информативных объясняющих
переменных размерности![]() :
:
 ;
;
![]() -
матрица размерности
-
матрица размерности![]() ,
транспонированная к матрице
,
транспонированная к матрице![]() .
.
Для определения
![]() используется встроенная статистическая
функцияСТЬЮДРАСПОБР(вероятность;степени_свободы)
пакета MSExcel, которая
возвращает t-значение распределения
Стьюдента как функцию вероятности и
числа степеней свободы:
используется встроенная статистическая
функцияСТЬЮДРАСПОБР(вероятность;степени_свободы)
пакета MSExcel, которая
возвращает t-значение распределения
Стьюдента как функцию вероятности и
числа степеней свободы:
Вероятность -вероятность, соответствующая двустороннему
распределению Стьюдента (уровень
значимости![]() );
);
Степени_свободы -число степеней свободы, характеризующее распределение.
Пример.Для
определения![]() при числе степеней свободы, равном7,
и уровне значимости
при числе степеней свободы, равном7,
и уровне значимости![]() =0,05необходимо ввести формулу=СТЬЮДРАСПОБР(0,05;7), результат
применения которой равняется2,364623.
=0,05необходимо ввести формулу=СТЬЮДРАСПОБР(0,05;7), результат
применения которой равняется2,364623.
В табл.2.9 рассмотрена методика выполнения операций с матрицами с помощью встроенных математических функций пакета MS Excel.
Таблица 2.9 – Примеры формул для выполнения основных операции с матрицами с помощью встроенных математических функций пакета MS Excel
|
Математическая формула |
Строк |
Столбцов |
Формула в пакете MS Excel (матрица Храсположена в ячейкахC2:E12; транспонированнаяматрица |
|
|
m+1 |
n |
=ТРАНСП(C2:E12) |
|
|
m+1 |
m+1 |
=МУМНОЖ(ТРАНСП(C2:E12);C2:E12) |
|
|
m+1 |
m+1 |
=МОБР(МУМНОЖ(ТРАНСП(C2:E12);C2:E12)) |
|
|
1 |
m+1 |
МУМНОЖ(C16:E16; МОБР(МУМНОЖ(ТРАНСП(C2:E12);C2:E12))) |
|
|
1 |
1 |
=МУМНОЖ(МУМНОЖ(C16:E16; МОБР(МУМНОЖ(ТРАНСП(C2:E12);C2:E12)));ТРАНСП(C16:E16)) |
Следовательно,
если матрица Храсположена в ячейкахC2:E12,
а прогнозные значения объясняющих
переменных расположены в виде
вектора-строки (т.е. представлены
транспонированной матрицей![]() )
в ячейкахC16:E16,
то для вычисления
)
в ячейкахC16:E16,
то для вычисления![]() вводим формулу:
вводим формулу:
=МУМНОЖ(МУМНОЖ(C16:E16; МОБР(МУМНОЖ(ТРАНСП(C2:E12);C2:E12)));ТРАНСП(C16:E16))
и нажимаем клавишу F2, затем клавишиCtrl+Shift+Enter.
7.Экономико-математический анализ характеристик эконометрической модели и выводы по работе формулируются по следующей схеме:
эконометрическая модель имеет вид:
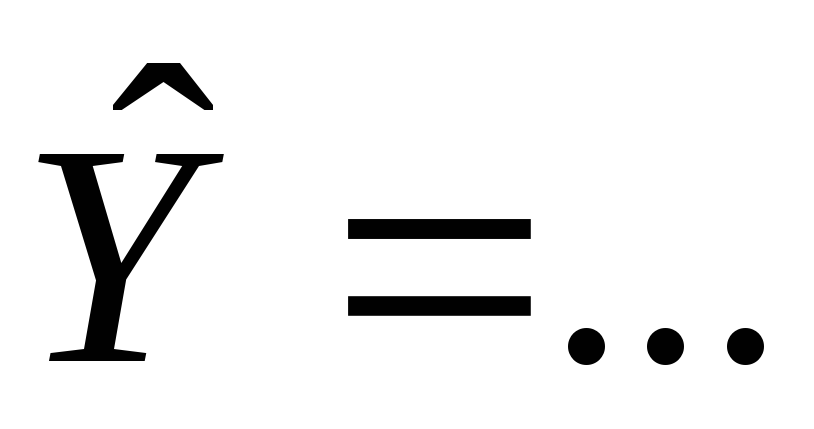 ,
где …;
,
где …;поскольку расчетное значение
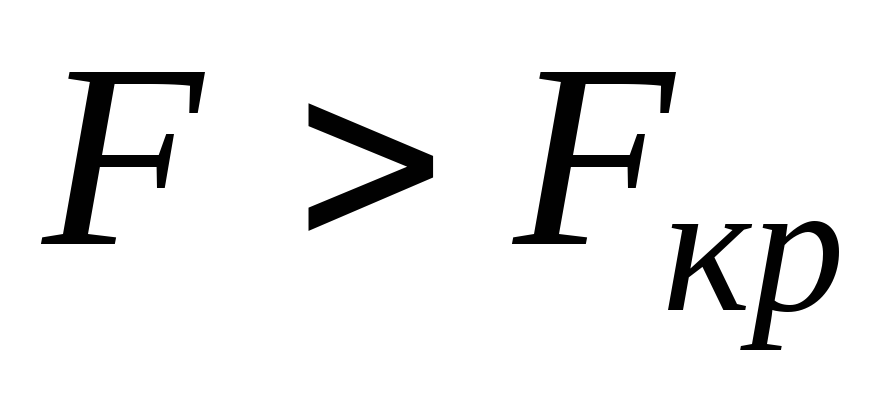 ,
то с надежностью ... построенную модель
можно считать адекватной наблюдаемым
данным и на основе этой модели можно
проводить экономический анализ и
находить значение прогноза;
,
то с надежностью ... построенную модель
можно считать адекватной наблюдаемым
данным и на основе этой модели можно
проводить экономический анализ и
находить значение прогноза;коэффициент детерминации
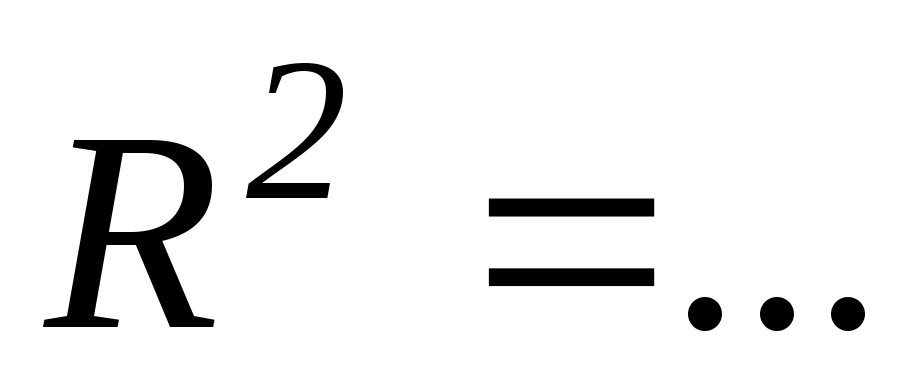 . Это означает, что на … % вариация чистой
прибыли зависит от …;
. Это означает, что на … % вариация чистой
прибыли зависит от …;поскольку для факторов … Р-значение меньше 0.05, то с надежностью … можно считать, что влияние факторов … на показатель Yзначительное и их необходимо учитывать в расчетах. В модели не учтено влияние фактора …, т.к. оно не существенно;
при изменении фактора
 на единицу и неизменной величине
факторов
на единицу и неизменной величине
факторов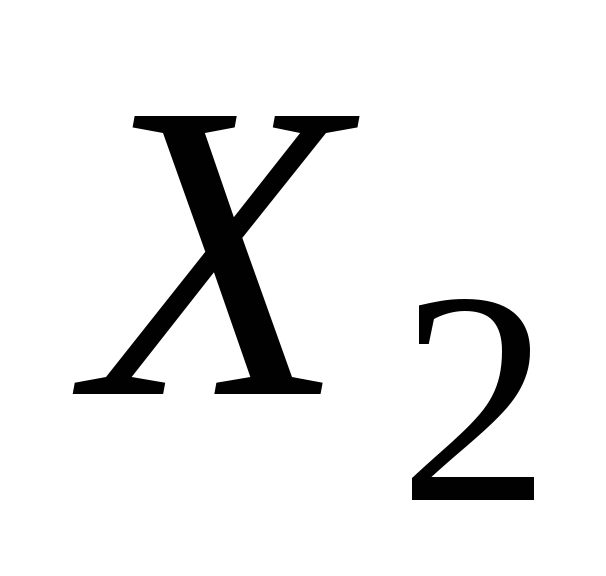 и
и показательYизменится на ... единиц;
показательYизменится на ... единиц;при изменении фактора
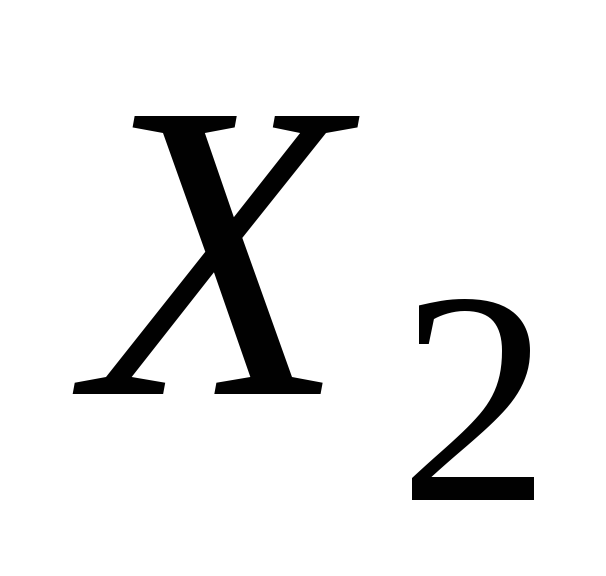 на единицу и неизменной величине
факторов
на единицу и неизменной величине
факторов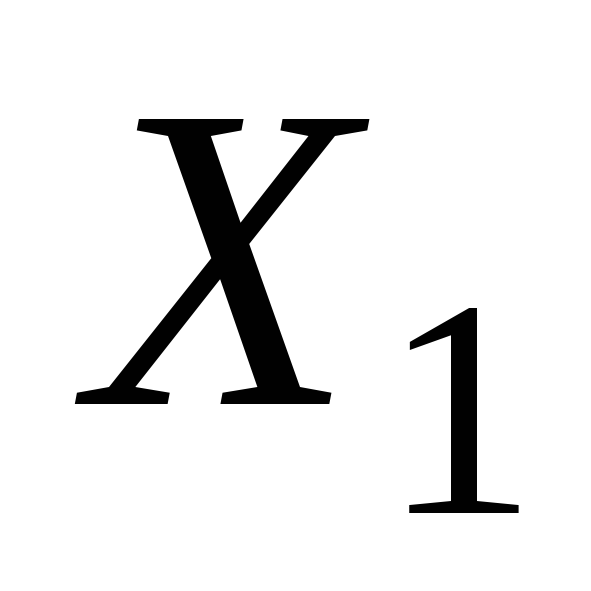 и
и показательYизменится на ... единиц;
показательYизменится на ... единиц;при изменении фактора
 на единицу и неизменной величине
факторов
на единицу и неизменной величине
факторов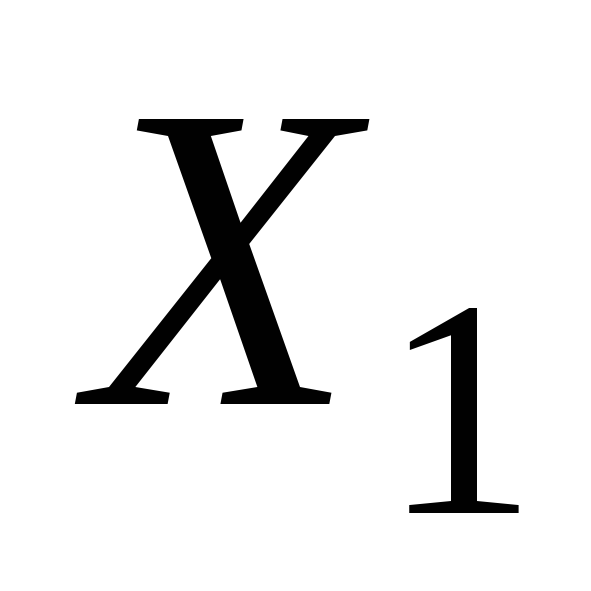 и
и показательYизменится на ... единиц;
показательYизменится на ... единиц;свободный член
 …
отражает средний эффект всех факторов,
которые влияют на показательY, за
исключением явно включенных в модель;
…
отражает средний эффект всех факторов,
которые влияют на показательY, за
исключением явно включенных в модель;для прогнозных значений факторов … среднее значение прогноза показателя … с надежностью ... будет находиться в пределах от ... до ...;
экономическая интерпретация: если в прогнозируемый период основные фонды составят … млн.грн., оборотные фонды – … млн.грн., а стоимость рабочей силы – … млн.грн., то с надежностью … средняя чистая прибыль попадает в интервал … млн.грн.