Методические рекомендации по выполнению работы

1.На основе исходного массива наблюдений с помощью инструментаАнализ Данных/Регрессияпакета MSExcelвыполняем построение линейной регрессионной модели. При этом должны быть установлены следующие флажки диалогового окна:График остатков,График подбора.

В отчете необходимо:

• привести таблицы регрессионного анализа;

• на основе таблиц результатов проанализировать статистическое качество модели;

• построить график остатков, график квадратов остатков и график подбора;

• выполнить графический анализ остатков на наличие гетероскедастичности.

Пример.

По исходным данным (табл.4.3) с помощью инструмента Анализа Данных/Регрессияпостроена линейная регрессия. Полученные при этом таблицы регрессионного анализа представлены в табл.4.4.

Тогда исходная регрессионная зависимость эконометрической модели имеет вид:

.

Проанализируем статистическое качество исходной эконометрической модели.

Коэффициент детерминации для этой модели (0,722489)статистически значим, и означает, что вариация сбережений на 72,25% определяется вариацией доходов населения. Модель в целом является статистически достоверной (значимостьF-статистики7,96E-06, что значительно меньше допустимого уровня значимости 0,05). Оценки всех параметров также статистически значимы, т.к. их Р-значения значительно меньше, чем 0,05.

На первый взгляд результат наводит на мысль, что спецификация модели не содержит ошибки.

Однако логично предположить, что стандартное отклонение величины сбережений для отдельных групп населения может меняться пропорционально среднему доходу этой группы. Эта ситуация вполне реалистична: люди с большим доходом имеют больший простор для его распределения. Поэтому для этой модели очень вероятно существование гетероскедастичности.

Таблица 4.3 – Исходные данные для примера

Наблюдение	X	Y
1	15	2,30
2	15	2,20
3	16	2,08
4	17	2,20
5	17	2,10
6	18	2,32
7	19	2,45
8	20	2,50
9	20	2,20
10	22	2,50
11	64	3,10
12	68	2,50
13	72	2,82
14	80	3,04
15	85	2,70
16	90	3,94
17	95	3,10
18	100	3,99

Таблица 4.4 – Регрессия по исходным данным обычным МНК

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,849994
R-квадрат	0,722489
Нормированный R-квадрат	0,705145
Стандартная ошибка	0,312088
Наблюдения	18
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	4,057193	4,057193	41,65538	7,96E-06
Остаток	16	1,558384	0,097399
Итого	17	5,615578
	Коэффици-енты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	1,99891	0,127227	15,71133	3,81E-11	1,729203	2,268623
X	0,01448	0,002243	6,454098	7,96E-06	0,009722	0,019232
ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки	е^2
1	2,216072	0,083928	0,007044
2	2,216072	-0,01607	0,000258
3	2,230549	-0,15055	0,022665
4	2,245026	-0,04503	0,002027
5	2,245026	-0,14503	0,021033
6	2,259504	0,060496	0,00366
7	2,273981	0,176019	0,030983
8	2,288458	0,211542	0,04475
9	2,288458	-0,08846	0,007825
10	2,317413	0,182587	0,033338
11	2,925458	0,174542	0,030465
12	2,983368	-0,48337	0,233644
13	3,041277	-0,22128	0,048963
14	3,157095	-0,11709	0,013711
15	3,229481	-0,52948	0,28035
16	3,301868	0,638132	0,407213
17	3,374254	-0,27425	0,075215
18	3,446641	0,543359	0,29524

Определиться с наличием гетероскедастичности позволяет использование графического представления остатков.

На графике изменения остатков регрессии , который получен в результатах регрессионного анализа, видна тенденция увеличения размаха остатков с увеличением значенияХ(рис.4.1).

Проанализируем теперь график изменения квадратов остатков регрессии , для построения которого в блок ВЫВОД ОСТАТКА (см. табл.4.4) добавим квадраты остатков (см. колонкуе^2), рассчитав их на основе данных колонкиОстатки.

Если все квадраты остатков находятся внутри полуполосы постоянной ширины, параллельной оси абсцисс, это говорит о независимости дисперсии остатков от значений переменнойХи их постоянстве, т.е. о выполнении условия гомоскедастичности.

В данном примере квадраты отклонений при больших значениях Хнамного больше, чем при малых, что говорит о наличии гетероскедастичности.

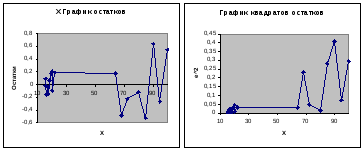
Рис.4.1. Графики остатков и квадратов остатков

В принципе и на графике подбора (рис 4.2) видно (хотя и не так явно), что разброс наблюдаемых точек относительно линии регрессии увеличивается с увеличением значения Х.

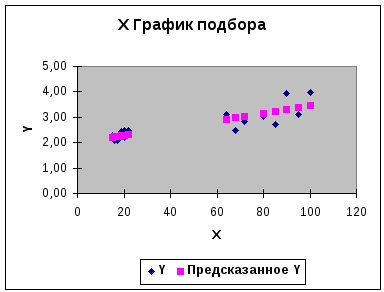
Рис.4.2. График подбора

2.Проверяем наличие гетероскедастичности с помощью параметрического теста Голдфелда-Квандта.

Пример.

Упорядочиммассив наблюдений (табл.4.3) в порядке возрастания наблюдаемых значений объясняющей переменнойХ(данные в табл.4.3 уже упорядочены).

Определяем оптимальное количество центральных наблюдений, которые необходимо отбросить:

.

Принимаем ближайшее , т.к. в этом случае после отбрасываниясредних наблюдений упорядоченной выборки получим две подвыборки одинаковой длины, одна из которых включаетмалыезначенияХ,а другая –большиезначенияХ.

С помощью обычного МНК оцениваем отдельные регрессии для первых и для последнихнаблюдений (табл.4.5):

• для оценивания регрессии на подвыборке, включающей малыезначенияХ, выделяем область пустых ячеекD3:E7, вводим формулу=ЛИНЕЙН(C3:C9;B3:B9;1;1), нажимаем клавишуF2, затем – комбинацию клавишCtrl+Shift+Enter;

• для оценивания регрессии на подвыборке, включающей большиезначенияХ, выделяем область пустых ячеекD14:E18, вводим формулу=ЛИНЕЙН(C14:C20;B14:B20;1;1), нажимаем клавишуF2, затем – комбинацию клавишCtrl+Shift+Enter.

Суммы квадратов остатков для первой и второй регрессии специально вычислять не надо, т.к. они содержатся в полученных с помощью встроенной статистической функции ЛИНЕЙНмассивах регрессионной статистики:

• для регрессии на подвыборке, включающей малыезначенияХ, – в ячейкеE7(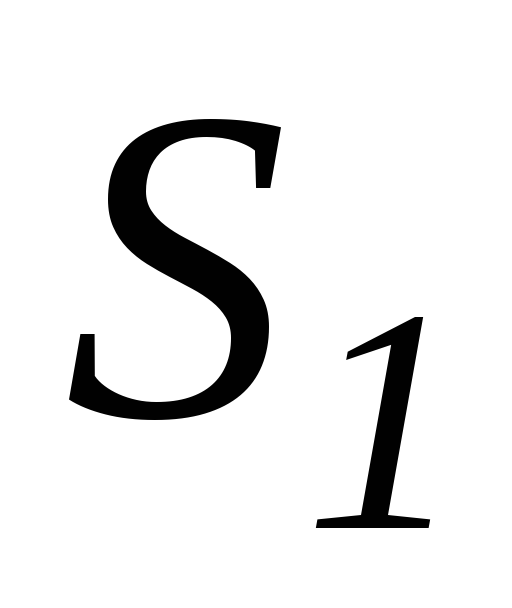=0,07453);

• для регрессии на подвыборке, включающей большиезначенияХ, – в ячейкеE18(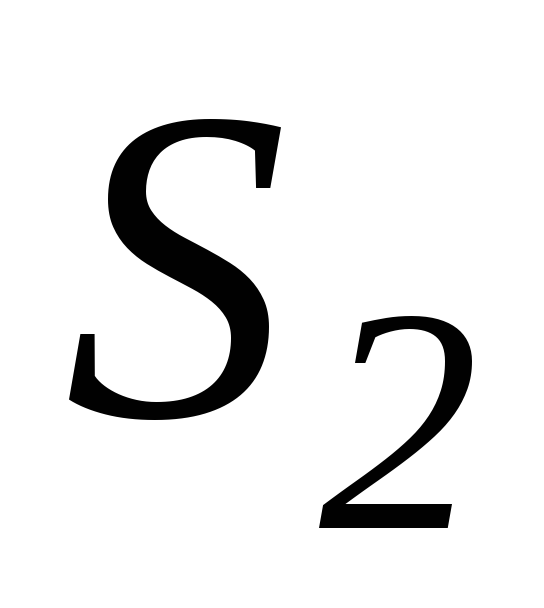=0,84581).

Таблица 4.5 – Параметрический тест Голдфелда-Квандта

	A	B	C	D	E	F	G
2	Наблюдение	X	Y	Регрессия для подвыборки из малых значений Х
3	1	15	2,30	0,04553	1,47468
4	2	15	2,20	0,03332	0,55879
5	3	16	2,08	0,27195	0,12209
6	4	17	2,20	1,86762	5
7	5	17	2,10	0,02784	0,07453
8	6	18	2,32
9	7	19	2,45
10	8	20	2,50
11	9	20	2,20
12	10	22	2,50
13	11	64	3,10	Регрессия для подвыборки из больших значений Х
14	12	68	2,50	0,03854	-0,0929
15	13	72	2,82	0,01428	1,21369
16	14	80	3,04	0,59296	0,41129
17	15	85	2,70	7,28391	5
18	16	90	3,94	1,23216	0,84581
19	17	95	3,10			F*=	11,3483
20	18	100	3,99			Fтабл=	5,050339

Рассчитываем статистику : в ячейкуG19вводим формулу=E18/E7, результат применения которой равняется11,3483.

Для определения табличного значения F-распределения Фишера при уровне значимости и числе степеней свободы;в ячейкуG20вводим формулу=FРАСПОБР(0,05;5;5), результат применения которой равняется5,050339.

В данном случае . Следовательно, с надежностью 0,95 в исходных данных имеет место гетероскедастичность.

3.Поскольку в исходных данных рассматриваемого примера гетероскедастичность выявлена, оценим параметры модели методом взвешенных наименьших квадратов, полагая что дисперсия остатков пропорциональна квадрату значений объясняющей переменнойХ.

Пример.

Разделив уравнение исходной модели на Х, после замены переменных вместо исходной модели с гетероскедастичностью, получим классическую регрессионную модель вида:

.

Значения преобразованных переменных вычисляем в ячейках J68:K85по формулам(табл.4.6). Для оценивания преобразованной модели обычным МНК с помощью встроенной статистической функцииЛИНЕЙН, выделяем блок пустых ячеекL68:M72, состоящий из двух столбцов (по числу оцениваемых параметров) и пяти строк, и вводим формулу

=ЛИНЕЙН(J68:J85;K68:K85;1;1)

Нажимаем клавишу F2, затем – клавишиCtrl+Shift+Enter.

Таблица 4.6 – Построение регрессии методом взвешенных наименьших квадратов

	J	K	L	M
67	Y/X	1/X	Оценки параметров ВМНК:
68	0,153333	0,066666667	2,011722998	0,01430815
69	0,146667	0,066666667	0,068591827	0,0029776
70	0,13	0,0625	0,981739006	0,00657418
71	0,129412	0,058823529	860,1845214	16
72	0,123529	0,058823529	0,037177047	0,00069152
73	0,128889	0,055555556
74	0,128947	0,052631579
75	0,125	0,05
76	0,11	0,05
77	0,113636	0,045454545
78	0,048438	0,015625
79	0,036765	0,014705882
80	0,039167	0,013888889
81	0,038	0,0125
82	0,031765	0,011764706
83	0,043778	0,011111111
84	0,032632	0,010526316
85	0,0399	0,01

Поскольку после преобразования модели параметры ипоменялись ролями, то в результатах применения функцииЛИНЕЙНэффективная оценка параметраисходной модели находится в ячейкеL68, а эффективная оценка параметра– в ячейкеM68. Следовательно, регрессионная зависимость эконометрической модели, оцененная ВМНК, имеет вид:

.

4.Строим матрицуSи матрицу.

Пример.

Вывод о наличии в исходных данных гетероскедастичности сделан на основе параметрического теста Голдфелда-Квандта, одним из условий применения которого является предположение о том, что дисперсия остатков изменяется пропорционально квадрату одной из объясняющих переменныхмодели.

Поэтому будет логичным, если мы для построения матрицы S(табл.4.7) и матрицы(табл.4.8) воспользуемся вторым случаем гетероскедастичности, т.е. будем полагать, что дисперсия остатков пропорциональна квадрату значений объясняющей переменнойХ. В этом случае для наших данных (табл.4.3). Следовательно,и.

Таблица 4.7 – Матрица S

	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z
2	Х^2	Матрица S
3	225	225	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
4	225	0	225	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
5	256	0	0	256	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
6	289	0	0	0	289	0	0	0	0	0	0	0	0	0	0	0	0	0	0
7	289	0	0	0	0	289	0	0	0	0	0	0	0	0	0	0	0	0	0
8	324	0	0	0	0	0	324	0	0	0	0	0	0	0	0	0	0	0	0
9	361	0	0	0	0	0	0	361	0	0	0	0	0	0	0	0	0	0	0
10	400	0	0	0	0	0	0	0	400	0	0	0	0	0	0	0	0	0	0
11	400	0	0	0	0	0	0	0	0	400	0	0	0	0	0	0	0	0	0
12	484	0	0	0	0	0	0	0	0	0	484	0	0	0	0	0	0	0	0
13	4096	0	0	0	0	0	0	0	0	0	0	4096	0	0	0	0	0	0	0
14	4624	0	0	0	0	0	0	0	0	0	0	0	4624	0	0	0	0	0	0
15	5184	0	0	0	0	0	0	0	0	0	0	0	0	5184	0	0	0	0	0
16	6400	0	0	0	0	0	0	0	0	0	0	0	0	0	6400	0	0	0	0
17	7225	0	0	0	0	0	0	0	0	0	0	0	0	0	0	7225	0	0	0
18	8100	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	8100	0	0
19	9025	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	9025	0
20	10000	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	10000

Таблица 4.8 – Матрица

	AB	AC	AD	AE	AF	AG	AH	AI	AJ	AK	AL	AM	AN	AO	AP	AQ	AR	AS	AT
2	1/X	Матрица P^-1
3	0,067	0,067	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
4	0,067	0	0,067	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
5	0,063	0	0	0,063	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
6	0,059	0	0	0	0,059	0	0	0	0	0	0	0	0	0	0	0	0	0	0
7	0,059	0	0	0	0	0,059	0	0	0	0	0	0	0	0	0	0	0	0	0
8	0,056	0	0	0	0	0	0,056	0	0	0	0	0	0	0	0	0	0	0	0
9	0,053	0	0	0	0	0	0	0,053	0	0	0	0	0	0	0	0	0	0	0
10	0,05	0	0	0	0	0	0	0	0,05	0	0	0	0	0	0	0	0	0	0
11	0,05	0	0	0	0	0	0	0	0	0,05	0	0	0	0	0	0	0	0	0
12	0,045	0	0	0	0	0	0	0	0	0	0,045	0	0	0	0	0	0	0	0
13	0,016	0	0	0	0	0	0	0	0	0	0	0,016	0	0	0	0	0	0	0
14	0,015	0	0	0	0	0	0	0	0	0	0	0	0,015	0	0	0	0	0	0
15	0,014	0	0	0	0	0	0	0	0	0	0	0	0	0,014	0	0	0	0	0
16	0,013	0	0	0	0	0	0	0	0	0	0	0	0	0	0,013	0	0	0	0
17	0,012	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0,012	0	0	0
18	0,011	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0,011	0	0
19	0,011	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0,011	0
20	0,01	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0,01

5.Оцениваем параметры модели обобщенным методом наименьших квадратов (ОМНК).

Пример.

Исходные данные, на основе которых строится модель, скопируем в ячейки A68:D85, как это представлено в табл.4.9.

Теперь матрица значений объясняющих переменных располагается в ячейкахB68:C85. В этой матрице каждая строка представляет наблюдение вектора значений независимых переменных (у нас один фактор – доход);единицасоответствует переменной при свободном члене.

Таблица 4.9 – Построение регрессии обобщенным методом наименьших квадратов

	A	B	C	D	E	F	G	H	I
67	Наблюдение	Х0	X	Y		Оценки параметров методом Эйткена:
68	1	1	15	2,30		b^0=	2,01172
69	2	1	15	2,20		b^1=	0,01431
70	3	1	16	2,08			Y*ср=	0,08888
71	4	1	17	2,20		Сумма квадратов отклонений:
72	5	1	17	2,10			Общая =	0,03787
73	6	1	18	2,32			Объяснен.=	0,03718
74	7	1	19	2,45
75	8	1	20	2,50		Остаточная дисперсия=		4,3E-05
76	9	1	20	2,20
77	10	1	22	2,50		Коэффициент детерминации
78	11	1	64	3,10			R^2=	0,9817
79	12	1	68	2,50		F=	860,1845	Fтабл=	4,494
80	13	1	72	2,82		Матрица ковариаций оценок параметров:
81	14	1	80	3,04		0,004704839	-0,000174
82	15	1	85	2,70		-0,000174404	8,87E-06
83	16	1	90	3,94
84	17	1	95	3,10		Ст.откл.b^0=	0,068592	tb0=	29,32890
85	18	1	100	3,99		Ст.откл.b^1=	0,002978	tb1=	4,80526
86	Сумма	18						tтабл=	2,1199
87						Доверительные интервалы для параметров:
88							Нижние 95%	Верхние 95%
89						b0=	1,866315	2,15713
90						b1=	0,007996	0,02062

Вектор-столбец наблюдений зависимой переменной (сбережения) располагается в ячейках D68:D85, а матрицаS– в ячейкахI3:Z20.

Для получения вектора оценок параметров модели методом Эйткена выделяем блок пустых ячеек G68:G69и для вычисления оператора оценивания (4.6) вводим формулу:

=МУМНОЖ( МОБР(МУМНОЖ(ТРАНСП(B68:C85);МУМНОЖ(МОБР(I3:Z20);B68:C85)));МУМНОЖ(ТРАНСП(B68:C85);МУМНОЖ(МОБР(I3:Z20);D68:D85)))

или

=МУМНОЖ( МОБР(МУМНОЖ(МУМНОЖ(ТРАНСП(B68:C85);МОБР(I3:Z20));B68:C85)); МУМНОЖ(МУМНОЖ(ТРАНСП(B68:C85);МОБР(I3:Z20));D68:D85))

Нажимаем клавишу F2, затем – клавишиCtrl+Shift+Enter.

В результате получим:

.

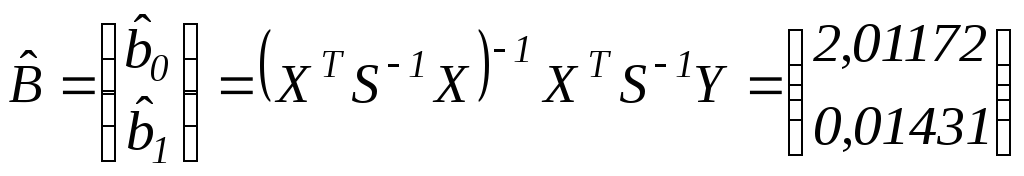Тогда регрессионная зависимость эконометрической модели имеет вид:

6.Проанализируем статистическое качество модели, параметры которой оценены обобщенным методом наименьших квадратов.

Пример.

6.1.Среднее по выборке значение скорректированной зависимой переменной (4.10): учитывая, что единичный вектор-столбец необходимой размерности находится в ячейкахB68:B85, диагональная матрица– в ячейкахAC3:AT20, а число наблюдений, в ячейкуH70вводим формулу

=МУМНОЖ(ТРАНСП(B68:B85);МУМНОЖ(AC3:AT20;D68:D85))/18

Нажимаем клавишу F2, затем – клавишиCtrl+Shift+Enter. В результате получим:

.

6.2.Общая сумма квадратов отклонений (4.8): учитывая, чтонаходится в ячейкеH70, в ячейкуH72вводим формулу

=МУМНОЖ(ТРАНСП(D68:D85);МУМНОЖ(МОБР(I3:Z20);D68:D85))-18*(H70^2)

Нажимаем клавишу F2, затем – клавишиCtrl+Shift+Enter. В результате получим:

.

Межгрупповая (объясненная) сумма квадратов отклонений (4.9): учитывая, что вектор-столбец находится в ячейкахG68:G69, в ячейкуH73вводим формулу

=МУМНОЖ(ТРАНСП(G68:G69);МУМНОЖ(ТРАНСП(B68:C85); МУМНОЖ(МОБР(I3:Z20);D68:D85)))-18*(H70^2)

Нажимаем клавишу F2, затем – клавишиCtrl+Shift+Enter. В результате получим:

.

6.3.Коэффициент детерминации без учета степеней свободы (4.13):

.

6.4.Проверим модель на адекватность по F-критерию Фишера. Для этого оценим статистическую значимость коэффициента детерминации:

• рассчитываем F-статистику: в ячейку G79вводим формулу=H78/(1-H78)*((18-1-1)/1), результат применения которой дает

=860,1845

где n– число наблюдений;m– число объясняющих переменных.

Величина F-статистики, если предположить, что выполнены предположения относительно ошибок, имеет распределение Фишера с степенями свободы;

• определяем табличное (критическое) значение F-распределения Фишера 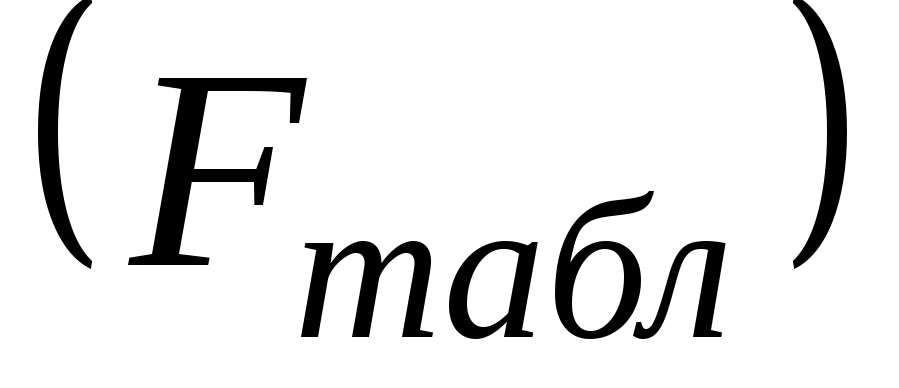при уровне значимости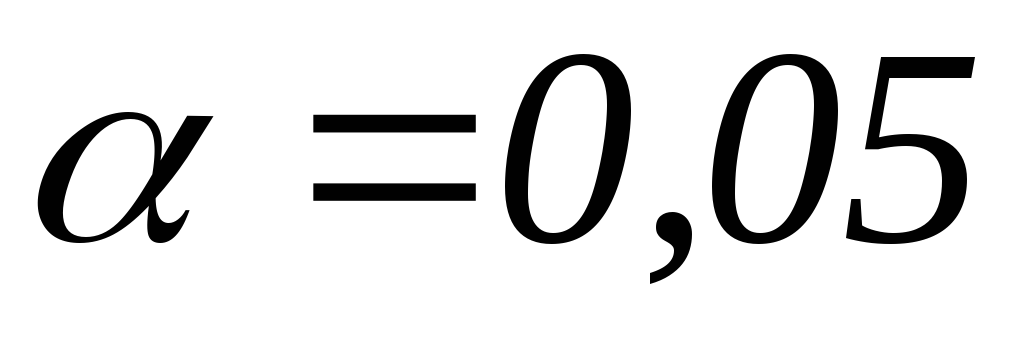и числе степеней свободы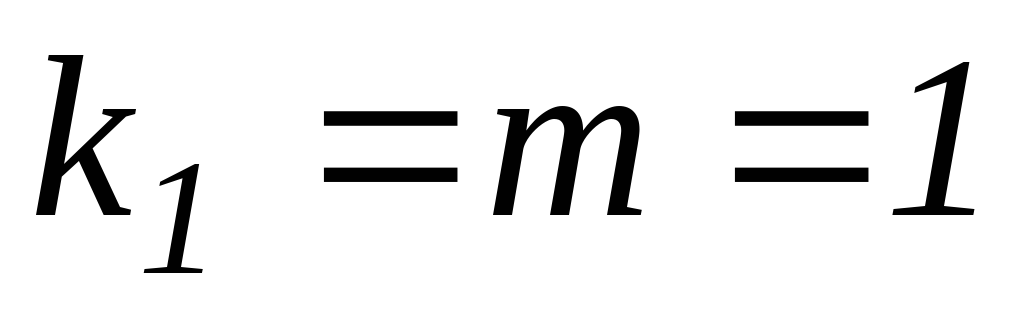;: в ячейкуI79вводим формулу=FРАСПОБР(0,05;1;16), результат применения которой равняется4,494.

• так как 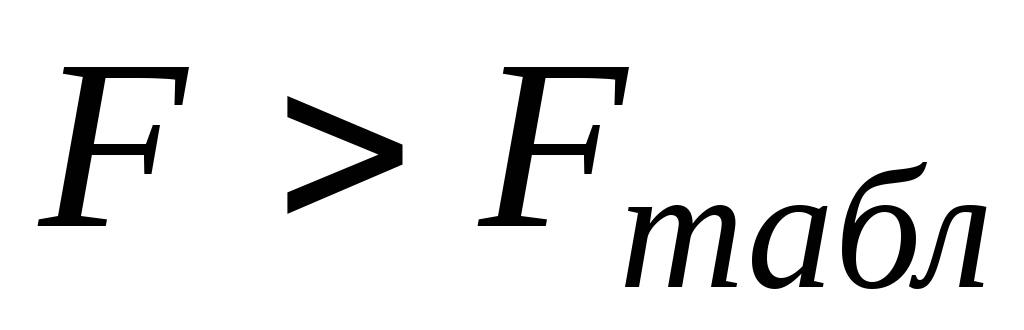, то с надежностью 0,95 полученное значение коэффициента детерминации статистически значимо, и, следовательно, модель в целом является статистически достоверной по F-критерию Фишера.

6.5.Несмещенная оценка остаточной дисперсии модели (4.14): в ячейкуH75вводим формулу

=МУМНОЖ( ТРАНСП(D68:D85-МУМНОЖ(B68:C85;G68:G69)); МУМНОЖ(МОБР(I3:Z20);(D68:D85-МУМНОЖ(B68:C85;G68:G69))))/(18-1-1)

Нажимаем клавишу F2, затем – клавишиCtrl+Shift+Enter.

В результате получим:

6.6.Для построения матрицы ковариаций вектораоценок параметров модели в соответствии с (4.15), выделяем блок пустых ячеекF81:G82и вводим формулу:

=H75*МОБР(МУМНОЖ(ТРАНСП(B68:C85);МУМНОЖ(МОБР(I3:Z20);B68:C85)))

Нажимаем клавишу F2, затем – клавишиCtrl+Shift+Enter.

Диагональные элементы построенной матрицы ковариаций являются оценками дисперсии оценок параметров модели. В результате получим:

• в ячейке F81– оценка дисперсии оценки параметра:

=0,004704839;

• в ячейке G82– оценка дисперсии оценки параметра:

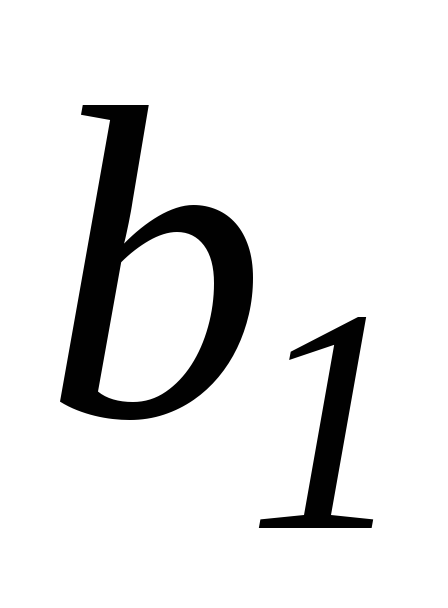=8,87E-06.

6.7.Оценки стандартных ошибок оценок параметров:

• в ячейку G84вводим формулу=КОРЕНЬ(F81), результат применения которой дает

0,068592;

• в ячейку G85вводим формулу=КОРЕНЬ(G82), результат применения которой дает

0,002978.

6.8.Воспользуемся Т-тестом Стьюдента для проверки статистической значимости оценок параметров модели.

Рассчитываем t-статистики для оценок параметров:

• в ячейку I84вводим формулу=G68/G84, результат применения которой дает

=29,32890;

• в ячейку I85вводим формулу=G69/G85, результат применения которой дает

=4,80526.

Рассчитанные t-статистики сравниваем с табличным критическим значением t-распределения Стьюдента при выбранном уровне значимости и степенях свободы , гдеk– количество оцененных параметров.

Для определения табличного значения t-критерия при уровне значимостии числе степеней свободы18-2=16в ячейкуI86вводим формулу=СТЬЮДРАСПОБР(0,05;(18-2)), результат применения которой равняется2,1199.

Поскольку в данном случае и, то с надежностью 0,95 оценки параметровистатистически достоверно отличаются от нуля, т.е. являются значимыми.

6.9.Доверительные интервалы для параметров модели строятся по формуле:

.

Тогда с надежностью 0,95 параметры модели могут находиться в следующих границах:

• в ячейку G89вводим формулу=G68-I86*G84; в ячейкуH89вводим формулу=G68+I86*G84, результат применения которых дает 95%-доверительный интервал для параметра:

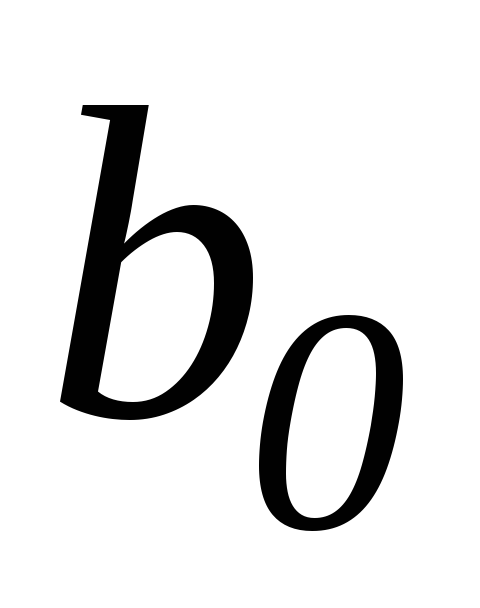1,8663152,15713;

• в ячейку G90вводим формулу=G69-I86*G85; в ячейкуH90вводим формулу=G69+I86*G85, результат применения которых дает 95%-доверительный интервал для параметра:

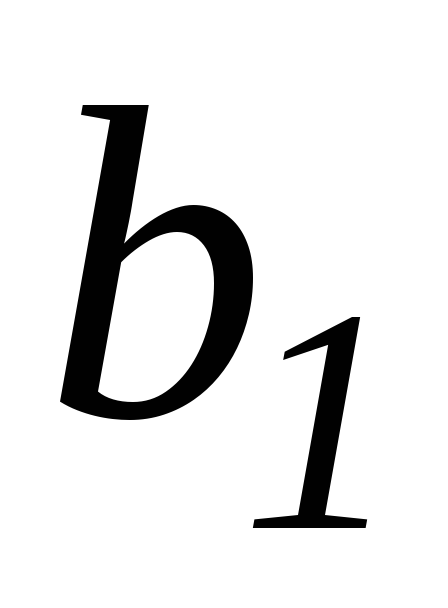0,0079960,02062.

7.Выполним экономико-математический анализ характеристик эконометрической модели.

Пример.

1.Регрессионная зависимость эконометрической модели, оцененная как ВМНК, так и ОМНК, имеет вид (в скобках указаны оценки стандартных ошибок оценок параметров):

	2,01172	+	0,01431·Х,		(4.16)
	(0,06859)		(0,00298)

Коэффициент детерминации . Это означает, что на 98,17% вариация величины сбережений зависит от величины дохода. Поскольку, то с надежностью 0,95 построенную регрессионную модель можно считать адекватной наблюдаемым данным и на основе этой модели можно проводить экономический анализ.

Остаточная (необъясненная) дисперсия .

Оценка параметра модели с надежностью 0,95 является статистически значимой. Увеличение дохода на единицу с надежностью 0,95 содействует предельному увеличению сбережений на величину от0,007996 до0,02062единиц.

Свободный член отражает средний эффект всех факторов, которые влияют на объем сбережений за исключением величины дохода.

2.Эконометрическая модель, параметры которой оценены по исходным данным обычным МНК, имеет вид:

	1,99891	+	0,01448·Х,		(4.17)
	(0,12723)		(0,00224)

Коэффициент детерминации . Это означает, что на 72,25% вариация величины сбережений зависит от величины дохода. Поскольку уровень значимостиF-статистики7,96E-06значительно меньше допустимого уровня значимости 0,05, то с надежностью 0,95 эту регрессионную модель также можно считать адекватной наблюдаемым данным. Здесь остаточная дисперсия. Отсюда, сравнив характеристики этой модели с моделью, параметры которой оценены ОМНК, можно утверждать, что в данном случае оценки, полученные ОМНК, эффективнее (остаточная дисперсия меньше).

3.Экономическая интерпретация: если, например, в прогнозируемый период доход составит 22 у.е., как этоимеет место в наблюдении №10, точечный прогноз величины сбережений составит:

=2,01172+0,01431·22=2,3265 у.е.