Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Эконометрия.doc

Скачиваний:

Добавлен:

03.03.2016

Размер:

5.1 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 133 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Комплексный пример основных расчетов по работе

1. Исходный массив 12 наблюдений расположен в ячейкахC3:G14(табл.2.10). Число исходных факторов – три. В табл.2.10 дополнительно введен фиктивный фактор, все значения которого равны 1.

Вычисляем средние значения исходных переменных, их дисперсии и стандартные отклонения. Затем входные данные переменных стандартизуем по формулам (2.3) и располагаем в ячейках P3:S14(табл.2.11).

Таблица 2.10 – Исходные данные в естественном масштабе

	B	C	D	E	F	G	H	I	J	K
2	Наблю- дение	Y	Х0	X1	X2	Х3	Yi-Yср	X1i-X1ср	X2i-X2ср	X3i-X3ср
3	1	14,2	1	21,4	17,1	12	-8,183333	-1,6	0,291667	2,75
4	2	8,1	1	19,2	6	11,5	-14,28333	-3,8	-10,8083	2,25
5	3	15,1	1	19,2	11,6	10,9	-7,283333	-3,8	-5,20833	1,65
6	4	7,5	1	15,6	10,3	10,6	-14,88333	-7,4	-6,50833	1,35
7	5	18,7	1	24,4	15,5	9,5	-3,683333	1,4	-1,30833	0,25
8	6	22,5	1	23,4	17,3	10	0,1166667	0,4	0,491667	0,75
9	7	25,4	1	21,1	19,7	9	3,0166667	-1,9	2,891667	-0,25
10	8	26,8	1	24,3	21,8	8,4	4,4166667	1,3	4,991667	-0,85
11	9	26,5	1	25,4	21	7,9	4,1166667	2,4	4,191667	-1,35
12	10	31,5	1	26,5	19,2	7,5	9,1166667	3,5	2,391667	-1,75
13	11	33,7	1	25,9	21,5	7,1	11,316667	2,9	4,691667	-2,15
14	12	38,6	1	29,6	20,7	6,6	16,216667	6,6	3,891667	-2,65
15	Сумма	268,6	12	276	201,7	111	-3,91E-14	0	-3,6E-15	0
16	Среднее	22,3833		23	16,8083	9,25
17	Ст.откл.
18
19
20	Коэффициенты корреляции:
21	rYX1=	0,9086	rX1X2=	0,771073
22	rYX2=	0,865967	rX1X3=	-0,82175
23	rYX3=	-0,9295	rX2X3=	-0,76435

Таблица 2.11 – Исходные данные в стандартизованном масштабе

+	L	M	N	O	P	Q	R	S
2	(Yi-Yср)^2	(X1i-X1ср)^2	(X2i-X2ср)^2	(X3i-X3ср)^2	Y*	X1*	X2*	X3*
3	66,96694	2,56	0,085069	7,5625	-0,86306	-0,43333	0,060159	1,607711
4	204,0136	14,44	116,8201	5,0625	-1,50641	-1,02916	-2,22932	1,3154
5	53,04694	14,44	27,12674	2,7225	-0,76814	-1,02916	-1,07427	0,964626
6	221,5136	54,76	42,3584	1,8225	-1,56969	-2,00415	-1,3424	0,78924
7	13,56694	1,96	1,711736	0,0625	-0,38847	0,379164	-0,26986	0,146156
8	0,013611	0,16	0,241736	0,5625	0,012304	0,108333	0,101411	0,438467
9	9,100278	3,61	8,361736	0,0625	0,318156	-0,51458	0,596432	-0,14616
10	19,50694	1,69	24,91674	0,7225	0,465808	0,352081	1,029576	-0,49693
11	16,94694	5,76	17,57007	1,8225	0,434169	0,649995	0,864569	-0,78924
12	83,11361	12,25	5,720069	3,0625	0,961499	0,94791	0,493303	-1,02309
13	128,0669	8,41	22,01174	4,6225	1,193524	0,785411	0,967698	-1,25694
14	262,9803	43,56	15,14507	7,0225	1,710308	1,787487	0,802691	-1,54925
15	1078,837	163,6	282,0692	35,11	-3,3E-15	0	-1,2E-15	0
16	89,90306	13,63333	23,50576	2,9258333
17	9,481722	3,692334	4,848274	1,7105067
18	Корреляционная матрица:
19		Y*	X1*	X2*	X3*
20	Y*	1
21	X1*	0,9086	1
22	X2*	0,865967	0,771073	1
23	X3*	-0,9295	-0,82175	-0,764349	1

2.Находим корреляционную матрицу.

Способ 1.

Элементы корреляционной матрицы находим с помощью встроенной статистической функцииКОРРЕЛпакета MSExcel:

для вычисления в ячейкуC21вводим формулу:=КОРРЕЛ(P3:P14;Q3:Q14)

для вычисления в ячейкуC22вводим формулу:=КОРРЕЛ(P3:P14;R3:R14)

для вычисления в ячейкуC23вводим формулу:=КОРРЕЛ(P3:P14;S3:S14)

для вычисления в ячейкуE21вводим формулу:=КОРРЕЛ(Q3:Q14;R3:R14)

для вычисления в ячейкуE22вводим формулу:=КОРРЕЛ(Q3:Q14;S3:S14)

для вычисления в ячейкуE23вводим формулу:=КОРРЕЛ(R3:R14;S3:S14)

Способ 2.

Вычисляем матрицу с помощью инструментаАнализа Данных «Корреляция»пакета MSExcel. Для этого в главном меню выбираем Сервис/Анализ данных/Корреляцияи заполняем диалоговое окноВходные данныеиПараметры выводаследующим образом:

Входной интервал–P2:S14(в первой строке – названия столбцов);
Группирование–по столбцам;
Метки в первой строке–устанавливаем флажок,который указывает, что в данном случае первая строкаP2:S2входного диапазонаP2:S14содержит названия столбцов;
Выходной интервал–L19– ссылка на левую верхнюю ячейку выходного диапазона.

Щелкнув по кнопке ОКв ячейкахL19:P23получим корреляционную матрицу (точнее – её нижний треугольник).

В корреляционной матрице находим: =0,9295,т.е. максимальноеуказывает на объясняющую переменную, которая теснее всего связана сY. Тогда методом наименьших квадратов найдем оценку параметра регрессии.

Для удобства выполнения дальнейших расчетов скопируем ранее вычисленные стандартизованные значения ив ячейкиC26:D38(табл.2.12). Поскольку в ячейкахP3:P14(табл.2.11) содержатся формулы, то при копировании из табл.2.11 в табл.2.12 вычисленных по этим формулам стандартизованных значенийY:

выделяем ячейки P2:P14(в ячейкеP2находится название столбца, а в ячейкахP3:P14– вычисленные стандартизованные значения);
находясь указателем в выделенной зоне нажимаем правую кнопку мыши и выбираем Копировать;
перемещаем курсор в ячейку C26, начиная с которой теперь будут располагаться значения;
нажимаем правую кнопку мыши, выбираем Специальная вставка…; в диалоговом окнеВставитьустанавливаем флажокзначенияи щелкаем по кнопкеОК.

Аналогично с помощью специальной вставкикопируем стандартизованные значенияиз ячеекS2:S14в ячейкиD26:D38.

Таблица 2.12 – Данные для расчета стандартизованных остатков регрессии на

	B	C	D	E	F	G	H	I	J
26	Наблюдение	Y*	X3*	Y*^X3	e^2yx3			Регрессия Y на Х3
27	1	-0,86306	1,607711	-1,49444	0,39863			-0,929543	0
28	2	-1,50641	1,3154	-1,22272	0,080478			0,111172	#Н/Д
29	3	-0,76814	0,964626	-0,89666	0,016517			0,864049	0,38511
30	4	-1,56969	0,78924	-0,73363	0,698987			69,9118	11
31	5	-0,38847	0,146156	-0,13586	0,063811			10,36859	1,631406
32	6	0,012304	0,438467	-0,40757	0,176297
33	7	0,318156	-0,14616	0,135858	0,033233
34	8	0,465808	-0,49693	0,461916	1,51E-05
35	9	0,434169	-0,78924	0,733632	0,089678
36	10	0,961499	-1,02309	0,951004	0,00011
37	11	1,193524	-1,25694	1,168377	0,000632
38	12	1,710308	-1,54925	1,440093	0,073016
39				Сумма=	1,631406

Теперь для нахождения оценки параметра регрессии (без свободного члена) выделяем блок пустых ячеекI27:J31, состоящий из двух столбцов и пяти строк, и вводим формулу

=ЛИНЕЙН(C27:C38;D27:D38;0;1)

Нажимаем клавишу F2, затем – клавишиCtrl+Shift+Enter. В результате в ячейкахI27:J31получаем таблицу регрессионной статистики, из первой строки которой следует, что=-0,9295.

По регрессионному уравнению в ячейкахE27:E38вычисляем прогнозные (расчетные) стандартизованные значения объясняемой переменнойпри расположенных в ячейкахD27:D38наблюдаемыхстандартизованных значениях объясняющей переменной.

В ячейках F27:F38вычисляем квадраты стандартизованных остатков, где- стандартизованные наблюдаемые значения объясняемой переменной, расположенные в ячейкахC27:C38. Затем в ячейкеF39вычисляем сумму квадратов остатков.

Среди тех значений коэффициентов корреляции , которые остались, выбираем следующее=0,9086и в модель вводим объясняющую переменную. Методом наименьших квадратов находим оценки параметров следующей регрессии в стандартизованном масштабе:

Особенность применения встроенной статистической функции ЛИНЕЙНдля оценивания параметров модели состоит в том, что наблюдаемые значения факторов должны быть расположены в виденепрерывной области. В данном случае это означает, что стандартизованные значенияидолжны располагаться в соседних столбцах. Поэтому скопируем ранее вычисленные стандартизованные значения,ииз табл.2.11 в ячейкиC42:E54(табл.2.13). Поскольку в ячейкахP3:S14содержатся формулы, то при копировании из табл.2.11 в табл.2.13 вычисленных по этим формулам стандартизованных значений переменных воспользуемсяспециальной вставкой.

Таблица 2.13 – Данные для расчета стандартизованных остатков регрессии наи

	B	C	D	E	F	G	H	I	J
42	Наблюдение	Y*	X1*	X3*	Y*^X1X3	e^2yx1x3		Регрессия Y на Х1,Х3
43	1	-0,86306	-0,43333	1,607711	-1,09868	0,055513		-0,56323	0,445769
44	2	-1,50641	-1,02916	1,3154	-1,19964	0,094106		0,14831	0,14831
45	3	-0,76814	-1,02916	0,964626	-1,00207	0,054723		0,928575	0,292763
46	4	-1,56969	-2,00415	0,78924	-1,33791	0,053719		65,00343	10
47	5	-0,38847	0,379164	0,146156	0,0867	0,225784		11,1429	0,857101
48	6	0,012304	0,108333	0,438467	-0,19867	0,044509
49	7	0,318156	-0,51458	-0,14616	-0,14706	0,21643		F=	9,034
50	8	0,465808	0,352081	-0,49693	0,436832	0,00084
51	9	0,434169	0,649995	-0,78924	0,734272	0,090062
52	10	0,961499	0,94791	-1,02309	0,998783	0,00139
53	11	1,193524	0,785411	-1,25694	1,058057	0,018351
54	12	1,710308	1,787487	-1,54925	1,66939	0,001674
55					Сумма=	0,857101

Теперь для нахождения оценок параметров регрессии в стандартизованном масштабе (без свободного члена) выделяем блок пустых ячеекI43:J47, состоящий из двух столбцов и пяти строк, и вводим формулу

=ЛИНЕЙН(C43:C54;D43:E54;0;1)

Нажимаем клавишу F2, затем – клавишиCtrl+Shift+Enter. В результате получаем таблицу регрессионной статистики, из первой строки которой следует, что=0,4458и=-0,5632.

По уравнению вычисляем прогнозные (расчетные) стандартизованные значения объясняемой переменной принаблюдаемыхстандартизованных значениях объясняющих переменныхи. Вычисляем квадраты стандартизованных остаткови сумму квадратов остатков.

С учетом того, что в первой модели один фактор , а во вторую модель добавлен только один новый фактор, находим расчетное значениеF-статистики:

Для уровня значимости и степеней свободы,по табл.2.8 находим табличное значениеF-статистики=4,96.

. Поэтому с принятой надежностьюможно считать, что помимо ранее включенного в модель факторановый фактортакже существенно влияет на показательY, и его необходимовключитьв модель.

Теперь в модель включаем оставшийся фактори оцениваем параметры уравнения регрессии с тремя факторами.

Для удобства вначале скопируем ранее вычисленные стандартизованные значения ,,и(табл.2.11) в ячейкиC58:F70(табл.2.14). Поскольку в ячейкахP3:S14содержатся формулы, копирование вычисленных по этим формулам стандартизованных значений переменных из табл.2.11 в табл.2.14 выполняем с помощьюспециальной вставки.

Таблица 2.14 – Данные для расчета стандартизованных остатков регрессии на,и

	B	C	D	E	F	G	H	I	J	K
58		Y*	X1*	X2*	X3*	Y*^ X1Х2X3	e^2 yx1х2x3	Регрессия Y на Х1,Х2,Х3
59	1	-0,86306	-0,43333	0,060159	1,607711	-0,86515	4,336E-06	-0,4586	0,2600	0,3313
60	2	-1,50641	-1,02916	-2,22932	1,3154	-1,5238	0,000303	0,13677	0,12240	0,13850
61	3	-0,76814	-1,02916	-1,07427	0,964626	-1,06262	0,086714	0,95243	0,25184	#Н/Д
62	4	-1,56969	-2,00415	-1,3424	0,78924	-1,37492	0,037935	60,0641	9	#Н/Д
63	5	-0,38847	0,379164	-0,26986	0,146156	-0,01158	0,142047	11,4292	0,57085	#Н/Д
64	6	0,012304	0,108333	0,101411	0,438467	-0,1388	0,022834
65	7	0,318156	-0,51458	0,596432	-0,14616	0,05163	0,071036	F=	4,51308
66	8	0,465808	0,352081	1,029576	-0,49693	0,612221	0,021437
67	9	0,434169	0,649995	0,864569	-0,78924	0,802054	0,135340
68	10	0,961499	0,94791	0,493303	-1,02309	0,911447	0,002505
69	11	1,193524	0,785411	0,967698	-1,25694	1,088199	0,011094
70	12	1,710308	1,787487	0,802691	-1,54925	1,511313	0,039599
71						Сумма=	0,570848

Теперь для нахождения оценок параметров регрессии в стандартизованном масштабе (без свободного члена) выделяем блок пустых ячеекI59:K63, состоящий из трех столбцов (по количеству факторов без свободного члена) и пяти строк, и вводим формулу

=ЛИНЕЙН(C59:C70;D59:F70;0;1)

Нажимаем клавишу F2, затем – клавишиCtrl+Shift+Enter. В результате получаем таблицу регрессионной статистики, из первой строки которой следует, что=0,3313,=0,2600,=-0,4586.

Рассчитываем квадраты стандартизованных остатков и сумму квадратов остатков.

Для оценки обоснованности включения фактора с учетом того, что в предыдущей модели два фактора, находим расчетное значениеF-статистики:

Для уровня значимости и степеней свободы,по табл.2.8 находим табличное значениеF-статистики=5,12.

. Следовательно, с принятой надежностьюможно считать, что факторнесущественновлияет на показательYи его необходимо исключить из модели. Тогда рациональным (окончательным) следует считать предыдущий вариант модели:

. (2.7)

3.Стандартизованные оценки параметровокончательного вариантамодели (2.7) по формулам (2.6) пересчитываемв естественный масштаб(табл.2.15):

для вычисления в ячейкуC75вводим формулу=J43*L17/M17, результат применения которой

=1,14471;

для вычисления в ячейкуC76вводим формулу=I43*L17/O17, результат применения которой

=-3,1221;

для вычисления в ячейкуC77вводим формулу=C16-(C75*E16+C76*G16), результат применения которой

=24,9345.

Тогда оцененное уравнение регрессии (2.7) в естественном масштабе будет иметь вид:

. (2.8)

Таблица 2.15 – Прогнозирование по линейной модели на,

	B	C	D	E	F	G	H	I
74	Оценки параметров в естественном масштабе:
75	b1=	1,144712
76	b3=	-3,12211
77	b0=	24,93448
78
79
80	Наблюдение	Y	Х0	X1	Х3
81	1	14,2	1	21,4	12		tтабл=	2,262159
82	2	8,1	1	19,2	11,5		Под корнем=	7,548006
83	3	15,1	1	19,2	10,9		Дельта Y=	18,18533
84	4	7,5	1	15,6	10,6
85	5	18,7	1	24,4	9,5	Дов.интервал для мат.ож. Yпр:
86	6	22,5	1	23,4	10		Нижние95%	Верхние95%
87	7	25,4	1	21,1	9		2,63002	39,00068
88	8	26,8	1	24,3	8,4
89	9	26,5	1	25,4	7,9
90	10	31,5	1	26,5	7,5
91	11	33,7	1	25,9	7,1
92	12	38,6	1	29,6	6,6
93	Прогноз	20,81535	1	34,04	13,8

4.Для построения с помощью инструментаАнализ Данных/Регрессияпакета MSExcelэконометрической модели вестественном масштабе, включающей отобранные ранее пошаговым регрессионным методом наиболее существенные факторыи, сформируем массив исходных данных в виде непрерывной области (входной интервал факторов должен быть ссылкой на непрерывную область!). Для этого скопируем исходные данные в естественном масштабе (с метками):

вектор-столбец Yиз ячеекC2:C14в ячейкиC80:C92;
вектор-столбец из ячеекE2:E14в ячейкиE80:E92;
вектор-столбец 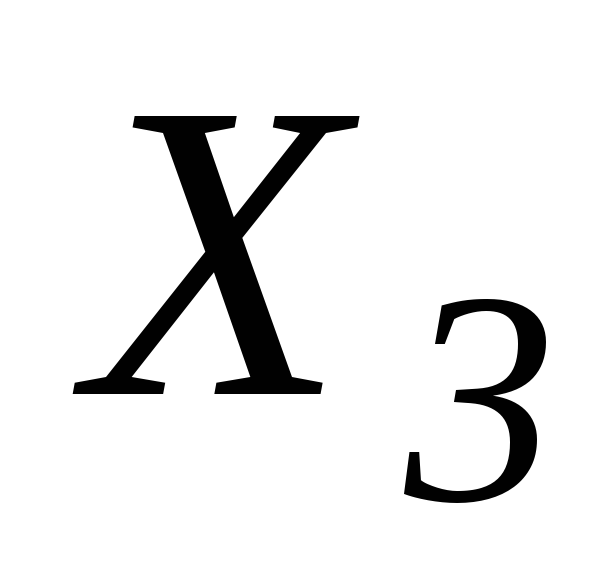из ячеекG2:G14в ячейкиF80:F92.

Далее в главном меню выбираем Сервис/Анализ данных/Регрессияи заполняем диалоговое окноВходные данные,Параметры выводаиОстаткиследующим образом:

Входной интервал Y–C80:C92(в ячейкеC80– название столбца –Y);
Входной интервал Х–E80:F92(в строке ячеекE80:F80– название столбцов – соответственноХ1иХ3);
Метки–устанавливаем флажок,указывающий, что первая строка массивовC80:C92иE80:F92содержит названия столбцов;
Выходной интервал–B95(левая верхняя ячейка будущего диапазона результатов);
устанавливаем флажок График остатков.

Щелкнув по кнопке ОК, получим результаты регрессионного анализа (табл.2.16), на основе которых должен быть выполнен анализ статистического качества эконометрической модели вестественном масштабе, включающей только отобранные ранее пошаговым регрессионным методом наиболее существенные факторыи. В табл.2.16 графики остатков не приведены. Анализ качества также не приводим.

Таблица 2.16 – Результаты регрессионного анализа линейной модели на,, полученные с помощью инструмента Анализа данных «Регрессия»

	B	C	D	E	F	G	H	I	J
95	ВЫВОД ИТОГОВ
96
97	Регрессионная статистика
98	Множественный R	0,963626
99	R-квадрат	0,928575
100	Нормированный R-квадрат	0,912703
101	Стандартная ошибка	2,926051
102	Наблюдения	12
103
104	Дисперсионный анализ
105		df	SS	MS	F	Значи-мость F
106	Регрессия	2	1001,781	500,8903	58,50308	6,96E-06
107	Остаток	9	77,05599	8,561777
108	Итого	11	1078,837
109
110		Коэффи-циенты	Стандартная ошибка	t-статис-тика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
111	Y-пересечение	24,93448	16,4884	1,512244	0,164762	-12,3649	62,233872	-12,36491	62,23387
112	X1	1,144712	0,401453	2,851421	0,019045	0,236561	2,0528631	0,236561	2,052863
113	Х3	-3,12211	0,866585	-3,60278	0,005723	-5,08246	-1,161758	-5,082464	-1,16176
114
115
116
117	ВЫВОД ОСТАТКА
118
119	Наблюдение	Предсказанное Y	Остатки
120	1	11,96599	2,234012
121	2	11,00868	-2,90868
122	3	12,88194	2,218056
123	4	9,697613	-2,19761
124	5	23,2054	-4,5054
125	6	20,49963	2,000365
126	7	20,98891	4,411092
127	8	26,52525	0,274746
128	9	29,34549	-2,84549
129	10	31,85352	-0,35352
130	11	32,41554	1,284462
131	12	38,21203	0,387972

5.В ячейкахE93:F93(табл.2.15) вычисляем прогнозные значения факторов, включенных в окончательный вариант модели (в соответствии с заданием принимаются на уровне1,15от максимальных значений этих факторов в исходных данных):

=34,04млн.грн.

=13,8млн.грн.

Точечный прогнозпоказателяYполучим подстановкой прогнозных значений отобранных факторов в полученное уравнение эконометрической модели в естественном масштабе (2.8):

=20,8153млн.грн.

6.Интервальный прогнозполучим в виде:

или

где

Для определения критического значения распределения Стьюдента приn-m-1=12-2-1=9степенях свободы и уровне значимости=0,05в ячейкуI81вводим формулу=СТЬЮДРАСПОБР(0,05;12-2-1), результат применения которой равняется2,26216.

Учитывая, что матрица Х наблюдаемых значений наиболее информативных факторов (с учетом единичного вектора фиктивной переменной при свободном члене) расположена в ячейкахD81:F92, а прогнозные значения вектора объясняющих переменных расположены в виде вектора-строки (т.е. представлены транспонированной матрицей) в ячейкахD93:F93, для вычисленияв ячейкуI82вводим формулу:

=МУМНОЖ(МУМНОЖ(D93:F93; МОБР(МУМНОЖ(ТРАНСП(D81:F92);D81:F92)));ТРАНСП(D93:F93))

Нажимаем клавишу F2, затем – клавишиCtrl+Shift+Enter.

Учитывая, что оценка стандартной ошибки оценивания была получена ранее в ячейкеC101, для вычисленияв ячейкуI83вводим формулу=I81*C101*КОРЕНЬ(I82), результат применения которой равняется18,1853.