Переход от задачи max к min и наоборот.

Во всех формах моделях все сводится к max, но иногда необходимо найти min/

Z=f(x)

min

z1max

z1=f(x)

Чтобы перейти от задачи min к max достаточно поменять знак и ввести новое значение функции.

Графический метод решения л.П.

Понятие: допустимого , оптимального , опорного решений, понятие области допустимых решений.

Вектор Х называется допустимым решением , если он удовлетворяет системе ограничений и условиям не отрицательности если они есть.

Вектор Х называется оптимальным решением если он является допустимым , а функция цели в этом решении достигает своего оптимального значения. (max or min)

Опорным решением называется не отрицательное базисное решение системы ограничений.

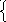
x1+x3 –x4=1

x2+2x3+4x4=-2

x1 и х2 –базисные неизвестные. Х3,х4 - неизвестные .

Приравняем свободные к 0. , тогда базисные неизвестные получают значения равные х1=1 х2=-2 и получаем базисное решение. Оно является не опорным , т.к. х=-2. Данное решение допустимое , базисное, не опорное.

Областью допустимых решений называется – совокупность всех допустимых решений системы.

Геометрическая интерпретация линейного неравенства.

n=2 a1x1+a2x2<=b (n-кол-во переменных , m число неравенств )

Из математики знаем что геометрическим образом уравнение а1х1+а2х2=b – прямая на плоскости х1 х2 Прямая разбивает плоскость на две полуплоскости . а1х1+а2х2<=b и >= , т.е. одно из плоскостей является решением. Чтобы определить какая четверть является решением данного неравенства нужно взять любую точку M и подставить в данное неравенство. И если не равенство удовлетворяется, то точка эта принадлежит той полуплоскости в которая является решением . И наоборот.

Геометрическая интерпретация системы линейны неравенств.

n=2 . a1x1+a1x2<=b1 ГИСЛН – является пересечение всех полуплоскостей соответству

a2x1+a2x2<=b2 ющих каждому неравенству системы , таким образом нашли ОДР.

am1x1+am2x2<=bm

Возможные случаи ОДР.

1. ОДР является точка.

2. ОДР выпуклый многоугольник.

3. ОДР выпуклая многоугольная область.

4. ОДР – пустая область

Графический метод .

ГМ состоит из двух этапов.

1. ОДР.

2. Среди всех решений необходимо найти такое решение при котором Z достигает своего либо max или min.

Grad показывает наискорейшее возрастание функции. (С – коэффициент) (линии уровня)

Возможные случаи

1. задача имеет единственное решение.

2. Задача имеет – бесконечно много решений.

3. Задача не имеет решений а) нет ОДР б) в случаи когда zmax - ф-ия не ограниченной сверху линией уровня и наоборот.

Графический метод можно применять если имеется только две переменные или задача может быть приведена с помощью эквивалентных преобразований к задаче с двумя переменными.

Опорный план. Свойства допустимых планов.

1. Выпуклая линейная комбинация точек . х1 х2 …хk сумма вида α1х1+ α2х2+ ...+ αkxk , где αi =1 (αi>=0 αi – коэффициент линейной комбинации).

2. Выпуклым множеством называется такое множество т. Д на плоскости , когда вместе с любыми двумя точками Х1є Д ; Х2 є Д принадлежащим множеству Д. Ему принадлежит и их выпуклая Л.К. х=tx1+(1-t)x2 є Д 0<=t<=1

3. Крайняя точка – т.Х выпуклого множества называется крайней если она не может быть представлена в виде выпуклой Л.К. любых двух точек этого множества (n=2)

Опорное решение – это допустимое базисное решение имеющая не более чем m положительных элементов , и причем векторы столбца матрицы соответственно положительны координатам вектора линейны независимы.