Метод Гаусса.
М.Г. вычисляется с помощью таблиц Гауса.
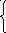2х1-х2+х3=3
х1+3х2-2х3=1 разрешающий элемнт.
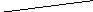
х2+2х3=8 разрешающая строка
разреш.столбец.
-
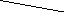
Х1Х2
Х3
Св.чл
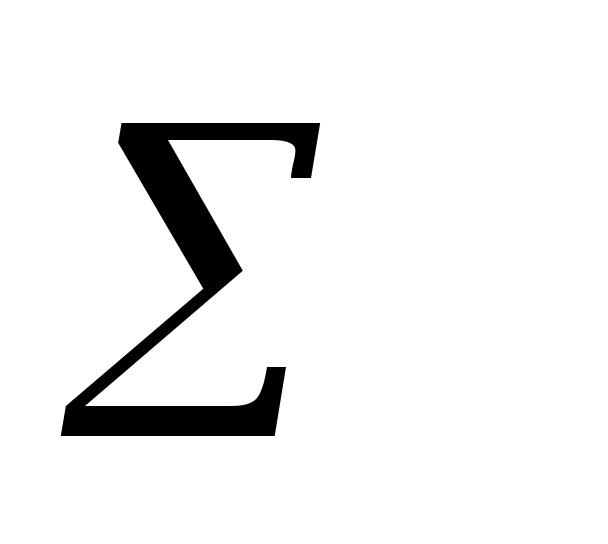
проверка
2
-1
1
3
5
5
1
3
-2
1
3
3
0
1
2
8
11
11
0
-7
5
1
-1
-1
1
3
-2
1
3
3
0
1
2
8
11
11
0
0
19
57
76
76
1
0
-8
-23
-30
-30
0
1
2
8
11
11
0
0
1
3
4
4
1
0
0
1
2
2
0
1
0
2
3
3
1)разрешающую
строку делим на разрешающий элемент.
2) в разрешающем столбце элементы заменяем
на ноли. 3) Все остальные элементы таблицы
считаются по правилу прямоугольника.
Переход от одной формы модели к другой форме модели , различные формы моделей з.Л.П.
В зависимости от системы ограничения различают в Л.П. три формы модели 1) каноническая 2) стандартная форма 3) общая форма. Эти три формы эквиваленты между собой в том смысле , что от одной формы можно перейти к другой с помощью элементарных преобразований.
Стандартная форма модели З.Л.П. . Система задачи формируется : Найти вектор х, удовлетворяющий системе ограничений и условию не отрицательности.
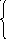
а11х1+а12х2+…+а1nxn<=b1
a21x1+a22x2+…+a2nxn<=b2
….
am1x1+am2x2+…+amnxn<=bn
xj>=0 j=1,4; Z=c1x1+c2x2+..+cnxn->max
A-матрица (m*n) Z=cx->max Ax<=b x>=0 ; C=(C1 C2 …Cn) b(b1 b2..bm)
Каноническаятоже самое только в системе ограничений = и Ax=b.
Общая форма. Найти вектор Х, удовлетворяющий системе ограничений
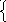a11x1+a12x2+...+a1nxn=b1
am1x1+amnxn=bm
Xj>=0 (j=1,l) l<n Для которого Z=с1х1+cnxn -> max
Для того что бы решать задачи Л.П. симплекс методом необходимо иметь каноническую форму модели, поэтому необходимо знать , как перейти от одной формы модели к другой .
Переход от стандартной формы к канонической форме.
ai1x1+ai2x2+…+ainxn<=bi (2)
ai1x1+ai2x2+..+ainxn+ainxi+n=b xn+i>=0 , i=1,m – балансовые переменные. (1)
Можно доказать, что все решения системы 1 равны решениям неравенства 2 и в этом сысле они эквивалентны. Функцию цели эти переменные(xn+i) могут быть введены с коэффициентами =0 => z=c1x1+..+cnxn+oXn+1+..+oxn+m->max
Переход от канонической к стандартной.
Осуществляется двумя способами.
1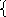
.
а=b (a>=b a<=b) -> a1x1+a2x2=b a1x1+a2x2>=b
a1x1+a2x2<=b
2. Z=c1x1+…+cnxn->max
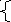a11x1+…+a1nxn=b1
a21x1+…+a2nxn=b2
am1x1+…+amnxn=bm (m<n – бесконечно много решений)
Приводим к единичному базису методом гауса. Приравняем все свободные переменные к 0, т.е. xm+1=xm+2=0 то получим первоначальное базисное решение.
Выражаем все базисные переменные через свободные.
Х1=b1-a1,m+1xm+1-..-a1,nxn>=0
Xm=bm-am,m+1-…-amnxn>=0
В функция цели вместо базисных переменных подставить их через переменные.
Z=c1(b1-..-a1nxn)+c2(b2-..-a2nxn)+cm(bm-..-amnxn)+cm+1xm+1+…+cnxn->max/