Переход от одного опорного плана к другому.

Необходимо перейти к другому опорному решению, т.е. одну из базисных переменных сделать свободной , а одну из свободных занять, так же как и симплекс метод. Для перехода используют замкнутую ломаную линию. Цикл 0 замкнутая ломаная линия вершины которой лежат в клетках а звенья лежат в строках и столбцах. Это ломаная должна быть связной в том смысле что в каждой вершине встречаются только два звена. Циклы могут быть самопересекающимися , при чем т. пересечения не является вершиной.

Цикл пересчета - называется цикл, одна вершина которого лежит в свободной клетке , а остальные в занятой. При переходе от одного плана к другому используются только циклы пересчета. λ>=0 λmin(xij) – i,j нечетные клетки цикла пересчета. Если в цикле пересчета в нескольких клетках разность будет равно 0 , то пишут базисный 0.

Проверка плана на оптимальность. Теорема об оптимальности плана или теорема о потенциальности плана.

Для док-ва составим двойственную к прямой задаче.

Z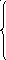=Cijxij->min

х11+х12+…+х1n =a1 ¦ -u1

x21+x22+…+x2n =a2 ¦ -u2

xm1+xm2+…+xmn = am ¦ -um

x11+ x21 +xm1 = b1 ¦ V1

x12+ x22+ xm2 = b2 ¦ V2

x1n+ x2n+ +xmn=bn ¦ Vn

xij>=0

V1-u1<=c11 Vm-Un<=C1n

Формулировка : Для того чтобы решения Х состоящее Х=¦xij¦ (i=1,m) (j=1,n) б было оптимальным для Т.З. необходимо и достаточно что бы существовала система из m+n чисел таки что бы выполнялось условия Vj-Ui<=Cij (для свободных клеток) Vj-Ui=Cij (для занятых)

Необходимость Х* - оптим. решение Т.З. Док-ть 1) и 2) условие

Если Х* оптим. решение прямой задачи то по 1-ой т. двойственности существует и решение двойственной задачи , т.е. существуют такие числа Vj & Ui такие что Vj-Ui<=Cij, - 1 условие

Хij(Vj-Ui-Cij)=0 но если клетка занятая то xij>=0 => Vj-Ui=Cij

Достаточность : Дано : Xij>=0 Vj-Ui=Cij

Доктть : Х* оптим решен.

2. -> перенеся Сij в левую часть и * Xij получим 0, это первое условие оптимальности плана поп второй т. двойственности. xij=ai ¦ -ui => (суммаXij –ai) ui =0 и (сумма Хij –bi)Vj=0 => второе условие оптимальности. => Х* оптимальное решение.

Алгоритм потенциалов.

Проверяем Vj-Ui=Cij и Vj-Ui<=Cij

Совместный учет производственных и

транспортных издержек.

Предположим что имеется m-производителей и n-покупателей.

A_i = (i = 1,m ) B_j= (j = 1.n )

Известны производственные затраты d_i (i = 1,n )

Спланировать перевозки так чтобы суммарные (производственные и транспортные) затраты были минимальными.

Нужно решить обычную транспортную задачу, затраты которой Cij = Cij + d

Блокирование перевозки или запрещение

перевозок.

Очень часто на практике при решение Т.З либо какой-то производитель или потребитель закладывает “запрет“ на продукцию.

Если это производитель – то он может запретить перевозку своего товара любому потребителю своей продукции.

Если это потребитель – то он может запретить перевозку товара к себе любому производителю с которым нехочет иметь дело.

В этом случае клетка с номером i , j должна быть заблокирована. И осуществляется это следующим образом. В клетку с номером i , j место Cij записываем число m (очень большое положительное число).