
- •Математическое программирование
- •Метод Гаусса.
- •Переход от одной формы модели к другой форме модели , различные формы моделей з.Л.П.
- •Переход от стандартной формы к канонической форме.
- •Переход от канонической к стандартной.
- •Переход от задачи max к min и наоборот.
- •Графический метод решения л.П.
- •Геометрическая интерпретация линейного неравенства.
- •Геометрическая интерпретация системы линейны неравенств.
- •Графический метод .
- •Опорный план. Свойства допустимых планов.
- •Свойства допустимых планов.
- •Идея симплекс метода.
- •Алгебра симплекс метода.
- •Альтернативный оптимум.
- •Монотонность и конечность алгоритма симплекс метода.
- •Проблема выражденности.
- •Метод искусственного базиса.
- •Теория двойственности.
- •Стандартная форма.
- •Правило построения двойственных задач к общей з.Л.П.
- •Теорема двойственности.
- •Вторая теорема двойственности и свойства двойственных оценок.
- •Свойства двойственных оценок.
- •Транспортная задача.
- •Особенности т.З.
- •Теорема о ранге матрицы.
- •Этапы решения т.З.
- •Метод нахождения первоначального опорного плана.
- •Переход от одного опорного плана к другому.
- •Проверка плана на оптимальность. Теорема об оптимальности плана или теорема о потенциальности плана.
- •Алгоритм потенциалов.
- •Задачи о назначении.
- •Математическая модель.
- •Алгоритм решения.
- •Задача коммивояжера.
- •Метод ветвей и границ.
- •Ветвлениею
- •Признак оптимальности.
Математическое программирование
Развитие направления относится к 30-ым годам. Математик – Толстой. Бурное развитие после войны. Всюду, где возникает необходимость выбора среди множества вариантов, решения какой либо проблемы (получения максимальной прибыли, минимальный расходы и.т.д) , выбор наилучшего в каком-то смысле – там и возникают задачи математического программирования.
Задачи записанные на языке формул, уравнений представляет собой математическое моделирование
Найти max или
min функции Z=f(![]() )
, где φ(
)
, где φ(![]() )
)![]() bi, где (i=1,k); φ(
bi, где (i=1,k); φ(![]() )=bi, где (i=1,k) (i=k+1, L);
)=bi, где (i=1,k) (i=k+1, L);![]()
![]() -
управляемый параметр.
-
управляемый параметр.![]() -
неуправляемый параметр. (не учитывается)
-
неуправляемый параметр. (не учитывается)
Чтобы решить задачу имея математическую модель нужно знать математические метод (Гауса, Крамера, матричный и.т.д) Зная метод => нужно знать алгоритм.
КЛАССИФИКАЦИЯ МЕТОДОВ.
В зависимости от того какими являются функции f и φi, задачи делятся на два класса : 1) Если функции f и φi линейны относительно параметров Х и У , то имеем задачу линейного программирования. (Л.П.)
2) Если хотя
бы одна из функций f и φi нелинейная
относительно параметров![]() и
и![]() ,
то имеем нелинейную задачу. (Н.П.)
,
то имеем нелинейную задачу. (Н.П.)
Для Л.П. существует универсальный способ. Симплекс – методОснов. разработку дал Дансон.
 Х3
Х3



 Х2
Х2
Х1
В Н.П. самым изученным является выпуклое программирование – это когда находится минимум выпуклой функции на выпуклом множестве или максимум вогнутой функции на выпуклом множестве. Существуют так же :1) Д.П. – динамическое программирование, вся задача разбивается на n-этапов. 2)Стохастическое программирование– случайные параметры. 3) Э.П. –эвристическое программирование, где оптимальное решение найти сложно из-за большого количества вариантов. 4) Ц.П. –целочисленное программирование.
Транспортная задача.
Имеется два пункта однородного продукта. Мощность 1го400т.; 2го– 500т., имеется 3 пункта потребления этого продукта. Известны затраты на перевозку 1т. продукции . Из 1гопункта к 1му– 2млн. р. ; 2му – 3 млн. р; 3му– 4 млн. р. Из 2го - 1му – 5 млн. р.;2му- 4 млн. р.; 3му- 2 млн. р. Спланировать перевод таким образом, чтобы суммарные затраты были минимальными.
1) нужно 300 т. 2) нужно 400 3) нужно 200 т.
Математическая модель.
Х
 ij– кол-во тонн продукции перевезенной
из пункта i к пункту j- му потребителю.
Найти план перевозок. (матрицу Х) Х= х11х12х13 Предложение =
спросу.
ij– кол-во тонн продукции перевезенной
из пункта i к пункту j- му потребителю.
Найти план перевозок. (матрицу Х) Х= х11х12х13 Предложение =
спросу.
Х21х22 х23 900 900
Если спрос и предложение совпадают , то имеем закрытую модель, иначе открытая модель. В закрытом моделирование все выражения равенства.
-
 bj
bjai
b1
300
b2
400
b3
200
400
2
x11
3
x12
4
x13
500
5
x21
4
x22
2
x23
b –потребность
.
![]() =
=![]()
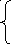 х11+x12+x13=400
х11+x12+x13=400
x21+x22+x23=500
2x11+x21=300
x12+x22=400
x13+x23=200
xij>=0 (i=
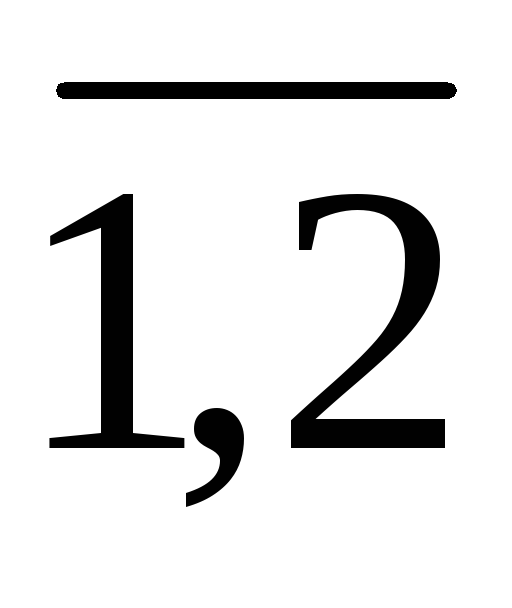 )
(j=
)
(j=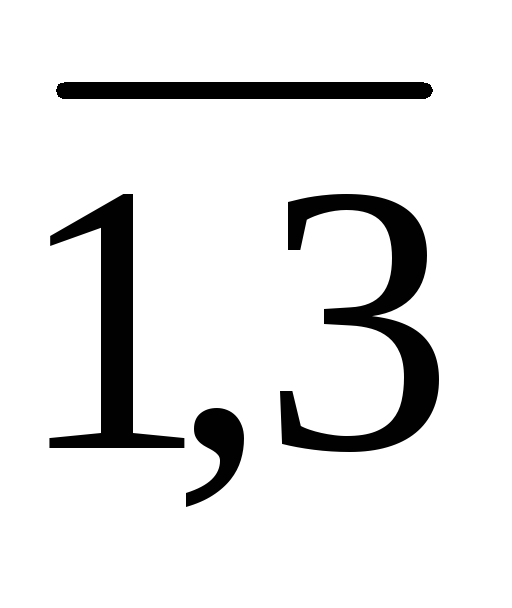 )
)
Функция цели 1Z=2x11+3x12+4x13+5x21+4x22+2x23 -> min
математическое моделирование задачи.
Различают другие типы задач :
1) задачи о диете или о рациональном питании.
2) задачи производственного планирования
3) на составление математического моделирования
4) задачи о раскрое
5) задачи о назначениях.
