
Математика для юристов - Д.А. Ловцова
.pdfРАЗДЕЛ I. Основания математики
ȿɫɥɢ ɜɫɟ ɩɪɟɫɬɭɩɥɟɧɢɹ, ɫɨɜɟɪɲɟɧɧɵɟ ɩɨ ɫɨɜɨɤɭɩɧɨɫɬɢ, ɹɜɥɹɸɬɫɹ ɩɪɟɫɬɭɩɥɟɧɢɹɦɢ ɧɟɛɨɥɶɲɨɣ ɢ ɫɪɟɞɧɟɣ ɬɹɠɟɫɬɢ, ɬɨ ɨɤɨɧɱɚɬɟɥɶɧɨɟ ɧɚɤɚɡɚɧɢɟ ɧɚɡɧɚɱɚɟɬɫɹ ɩɭɬɟɦ ɩɨɝɥɨɳɟɧɢɹ ɦɟɧɟɟ ɫɬɪɨɝɨɝɨ ɧɚɤɚɡɚɧɢɹ ɛɨɥɟɟ ɫɬɪɨɝɢɦ ɥɢɛɨ ɩɭɬɟɦ ɱɚɫɬɢɱɧɨɝɨ ɢɥɢ ɩɨɥɧɨɝɨ ɫɥɨɠɟɧɢɹ
ɧɚɡɧɚɱɟɧɧɵɯ ɧɚɤɚɡɚɧɢɣ.
(ɍɄ ɊɎ, ɋɬ. 69, ɱ. 2)
Глава 1. Элементы теории множеств
1.1. Понятие множества
Ɇɧɨɠɟɫɬɜɨ – ɨɞɧɨ ɢɡ ɩɟɪɜɢɱɧɵɯ, ɮɭɧɞɚɦɟɧɬɚɥɶɧɵɯ ɩɨɧɹɬɢɣ ɦɚɬɟɦɚɬɢɤɢ. Ɉɞɧɚɤɨ ɫɬɪɨɝɨɝɨ ɨɩɪɟɞɟɥɟɧɢɹ ɷɬɨɝɨ ɩɨɧɹɬɢɹ ɜ ɪɚɦɤɚɯ ɫɚɦɨɣ ɬɟɨɪɢɢ ɦɧɨɠɟɫɬɜ ɧɟ ɫɭɳɟɫɬɜɭɟɬ. ȿɝɨ ɦɨɠɧɨ ɥɢɲɶ ɩɨɹɫɧɢɬɶ, ɩɪɢɜɟɞɹ ɩɪɢɦɟɪɵ ɦɧɨɠɟɫɬɜ. ɋɤɚɠɟɦ, ɦɧɨɠɟɫɬɜɨ ɫɬɭɞɟɧɬɨɜ ɩɟɪɜɨɝɨ ɤɭɪɫɚ ɚɤɚɞɟɦɢɢ, ɦɧɨɠɟɫɬɜɨ ɡɚɤɨɧɨɞɚɬɟɥɶɧɵɯ ɚɤɬɨɜ ɩɨ ɩɪɚɜɚɦ ɱɟɥɨɜɟɤɚ, ɦɧɨɠɟɫɬɜɨ ɩɹɬɟɧ ɧɚ ɋɨɥɧɰɟ ɢ ɬ.ɞ.
Ɉɛɴɟɤɬɵ, ɫɨɫɬɚɜɥɹɸɳɢɟ ɦɧɨɠɟɫɬɜɨ, ɧɚɡɵɜɚɸɬ ɷɥɟɦɟɧɬɚɦɢ. Ʉɨɝɞɚ ɷɬɨ ɭɞɨɛɧɨ, ɷɥɟɦɟɧɬɵ ɦɧɨɠɟɫɬɜɚ ɧɚɡɵɜɚɸɬ ɬɨɱɤɚɦɢ (ɧɚɩɪɢɦɟɪ, ɷɥɟɦɟɧɬɵ ɦɧɨɠɟɫɬɜɚ ɜɟɳɟɫɬɜɟɧɧɵɯ ɱɢɫɟɥ – ɬɨɱɤɢ ɧɚ ɱɢɫɥɨɜɨɣ ɩɪɹɦɨɣ). ȼ ɬɟɨɪɢɢ ɦɧɨɠɟɫɬɜ, ɤɚɤ ɢ ɜ ɥɸɛɨɣ ɦɚɬɟɦɚɬɢɱɟɫɤɨɣ ɬɟɨɪɢɢ, ɢɫɩɨɥɶɡɭɸɬ ɫɜɨɸ ɫɢɫɬɟɦɭ ɨɛɨɡɧɚɱɟɧɢɣ. Ɍɚɤ, ɫɚɦɢ ɦɧɨɠɟɫɬɜɚ ɨɛɨɡɧɚɱɚɸɬ ɩɪɨɩɢɫɧɵɦɢ ɛɭɤɜɚɦɢ A, B, X, Y, ɚ ɞɥɹ ɨɛɨɡɧɚɱɟɧɢɹ ɷɥɟɦɟɧɬɨɜ ɢɫɩɨɥɶɡɭɸɬ ɫɬɪɨɱɧɵɟ ɛɭɤɜɵ a, b, x, y. ȿɫɥɢ a – ɷɥɟɦɟɧɬ ɦɧɨɠɟɫɬɜɚ A, ɬɨ ɝɨɜɨɪɹɬ, ɱɬɨ a ɩɪɢɧɚɞɥɟɠɢɬ A, ɢ ɷɬɨɬ ɮɚɤɬ ɡɚɞɚɸɬ ɬɚɤɨɣ ɡɚɩɢɫɶɸ: a A. ȿɫɥɢ ɠɟ a ɧɟ ɹɜɥɹɟɬɫɹ ɷɥɟɦɟɧɬɨɦ ɦɧɨɠɟɫɬɜɚ A, ɬɨ ɩɢɲɭɬ: a A, ɢ ɝɨɜɨɪɹɬ, ɱɬɨ a ɧɟ ɩɪɢɧɚɞɥɟɠɢɬ A.
Ɋɚɡɥɢɱɚɸɬ ɤɨɧɟɱɧɵɟ ɦɧɨɠɟɫɬɜɚ ɢ ɛɟɫɤɨɧɟɱɧɵɟ. Ʉɨɧɟɱɧɨɟ ɦɧɨɠɟɫɬɜɨ ɫɨɫɬɨɢɬ ɢɡ ɤɨɧɟɱɧɨɝɨ ɱɢɫɥɚ ɷɥɟɦɟɧɬɨɜ, ɩɪɢɱɟɦ ɧɟɜɚɠɧɨ: ɢɡɜɟɫɬɧɨ ɷɬɨ ɱɢɫɥɨ ɢɥɢ ɧɟɬ, ɝɥɚɜɧɨɟ, ɱɬɨ ɨɧɨ ɫɭɳɟɫɬɜɭɟɬ. Ɉɛɳɟɟ ɱɢɫɥɨ ɷɥɟɦɟɧɬɨɜ ɜ ɤɨɧɟɱɧɨɦ ɦɧɨɠɟɫɬɜɟ ɧɚɡɵɜɚɸɬ ɟɝɨ ɦɨɳɧɨɫɬɶɸ. Ʉɨɥɢɱɟɫɬɜɨ ɷɥɟɦɟɧɬɨɜ ɜ ɛɟɫɤɨɧɟɱɧɨɦ ɦɧɨɠɟɫɬɜɟ ɩɨɞɫɱɟɬɭ ɧɟ ɩɨɞɞɚɟɬɫɹ, ɞɚɠɟ ɬɟɨɪɟɬɢɱɟɫɤɢ.
Ɂɚɞɚɬɶ ɤɨɧɟɱɧɨɟ ɦɧɨɠɟɫɬɜɨ ɦɨɠɧɨ, ɩɪɨɫɬɨ ɩɟɪɟɱɢɫɥɢɜ ɟɝɨ ɷɥɟɦɟɧɬɵ. ɇɚɩɪɢɦɟɪ, ɦɧɨɠɟɫɬɜɨ X ɢɡ n ɷɥɟɦɟɧɬɨɜ: X {x1, x2, , xn}. ȼ ɱɚɫɬɧɨɫɬɢ, ɩɪɢ n 1 ɢɦɟɟɦ ɨɞɧɨɷɥɟɦɟɧɬɧɨɟ ɦɧɨɠɟɫɬɜɨ X {x1}. Ɉɞɧɚɤɨ ɩɪɨɫɬɨɟ ɩɟɪɟɱɢɫɥɟɧɢɟ ɷɥɟɦɟɧɬɨɜ ɦɧɨɠɟɫɬɜɚ ɧɟɭɞɨɛɧɨ ɞɥɹ ɛɨɥɶɲɢɯ n ɢ ɜɨɜɫɟ ɧɟ ɝɨɞɢɬɫɹ ɞɥɹ ɡɚɞɚɧɢɹ ɛɟɫɤɨɧɟɱɧɵɯ ɦɧɨɠɟɫɬɜ.
11
ȼɵɯɨɞ ɢɡ ɷɬɨɣ ɫɢɬɭɚɰɢɢ – ɡɚɞɚɬɶ ɦɧɨɠɟɫɬɜɨ ɨɩɢɫɚɧɢɟɦ ɫɜɨɣɫɬɜ ɟɝɨ ɷɥɟɦɟɧɬɨɜ (ɫ ɩɨɦɨɳɶɸ ɯɚɪɚɤɬɟɪɢɫɬɢɱɟɫɤɨɝɨ ɫɜɨɣɫɬɜɚ ɦɧɨɠɟɫɬɜɚ). ɉɭɫɬɶ ɜɫɟ ɷɥɟɦɟɧɬɵ x ɦɧɨɠɟɫɬɜɚ X ɨɛɥɚɞɚɸɬ ɫɜɨɣɫɬɜɨɦ P(x). Ɍɨɝɞɚ ɷɬɨ ɦɧɨɠɟɫɬɜɨ ɡɚɞɚɟɬɫɹ ɬɚɤɨɣ ɤɨɧɫɬɪɭɤɰɢɟɣ: X {x: P(x)}. ȿɟ ɱɢɬɚɸɬ ɬɚɤ: ɦɧɨɠɟɫɬɜɨ X, ɫɨɫɬɨɹɳɟɟ ɢɡ ɷɥɟɦɟɧɬɨɜ x ɬɚɤɢɯ, ɱɬɨ ɤɚɠɞɵɣ ɢɡ ɧɢɯ ɨɛɥɚɞɚɟɬ ɫɜɨɣɫɬɜɨɦ P(x). ɋɤɚɠɟɦ, ɦɧɨɠɟɫɬɜɨ
A {1, 2, 3, 4, 5} ɦɨɠɧɨ ɡɚɞɚɬɶ ɢ ɬɚɤ: A {x: x N ɢ x 6}, ɝɞɟ N – ɦɧɨɠɟɫɬ-
ɜɨ ɧɚɬɭɪɚɥɶɧɵɯ ɱɢɫɟɥ. ȿɳɟ ɩɪɢɦɟɪ. Ɉɬɪɟɡɤɨɦ [a,b] ɧɚɡɵɜɚɟɬɫɹ ɬɚɤɨɟ ɦɧɨɠɟɫɬɜɨ: [a,b] {x R: adxdb}. Ɏɪɚɡɭ ɷɬɭ ɦɨɠɧɨ ɩɪɨɱɟɫɬɶ ɬɚɤ: ɨɬɪɟɡɨɤ [a,b] – ɷɬɨ ɷɥɟɦɟɧɬɵ x ɢɡ ɦɧɨɠɟɫɬɜɚ R ɜɟɳɟɫɬɜɟɧɧɵɯ ɱɢɫɟɥ, ɡɧɚɱɟɧɢɹ ɤɨɬɨɪɵɯ ɛɨɥɶɲɟ ɢɥɢ ɪɚɜɧɵ a ɢ ɦɟɧɶɲɟ ɢɥɢ ɪɚɜɧɵ b. Ⱥ ɡɚɩɢɫɶ ]a,b[ {x R: a x b} ɡɚɞɚɟɬ ɦɧɨɠɟɫɬɜɨ, ɧɚɡɵɜɚɟɦɨɟ ɢɧɬɟɪɜɚɥɨɦ ɫ ɨɬɤɪɵɬɵɦɢ ɝɪɚɧɢɰɚɦɢ (ɷɥɟɦɟɧɬɵ x ɢɡ ɦɧɨɠɟɫɬɜɚ ɜɟɳɟɫɬɜɟɧɧɵɯ ɱɢɫɟɥ ɬɚɤɢɟ, ɱɬɨ ɢɯ ɡɧɚɱɟɧɢɹ ɫɬɪɨɝɨ ɛɨɥɶɲɟ a ɢ ɦɟɧɶɲɟ b).
ȿɫɥɢ ɦɧɨɠɟɫɬɜɨ A ɹɜɥɹɟɬɫɹ ɱɚɫɬɶɸ ɦɧɨɠɟɫɬɜɚ B, ɬɨ ɝɨɜɨɪɹɬ, ɱɬɨ A ɟɫɬɶɩɨɞɦɧɨɠɟɫɬɜɨ B. Ɂɚɩɢɫɵɜɚɟɬɫɹɷɬɨɨɬɧɨɲɟɧɢɟɦɧɨɠɟɫɬɜɬɚɤ: A B. Ⱥ ɡɚɩɢɫɶ B A ɝɨɜɨɪɢɬɨɬɨɦ, ɱɬɨ B ɟɫɬɶɩɨɞɦɧɨɠɟɫɬɜɨ A.
Ɇɧɨɠɟɫɬɜɚ A ɢ B ɧɚɡɵɜɚɸɬ ɪɚɜɧɵɦɢ, ɤɨɝɞɚ ɨɧɢ ɫɨɫɬɨɹɬ ɢɡ ɨɞɧɢɯ ɢ ɬɟɯ ɠɟ ɷɥɟɦɟɧɬɨɜ. ɇɚ ɹɡɵɤɟ ɬɟɨɪɢɢ ɦɧɨɠɟɫɬɜ ɷɬɨ ɡɚɩɢɫɵɜɚɸɬ ɬɚɤ: A B. ɇɚɩɪɢɦɟɪ, ɦɧɨɠɟɫɬɜɚ A {3,5,7,9} ɢ B {7,3,9,5} ɫɨɫɬɨɹɬ ɢɡ ɨɞɧɢɯ ɢ ɬɟɯ ɠɟ ɷɥɟɦɟɧɬɨɜ, ɡɧɚɱɢɬ, ɨɧɢ ɪɚɜɧɵ.
Ɇɧɨɠɟɫɬɜɚ A ɢ B ɪɚɜɧɵ ɬɨɝɞɚ, ɤɨɝɞɚ ɨɞɧɨɜɪɟɦɟɧɧɨ ɜɵɩɨɥɧɹɸɬɫɹ ɭɫɥɨɜɢɹ:
ɟɫɥɢ x A, ɬɨ x B, ɟɫɥɢ x B, ɬɨ x A.
ɇɚɩɪɢɦɟɪ, A – ɦɧɨɠɟɫɬɜɨ ɜɫɟɯ ɱɟɬɧɵɯ ɩɨɥɨɠɢɬɟɥɶɧɵɯ ɱɢɫɟɥ, B – ɦɧɨɠɟɫɬɜɨ ɩɨɥɨɠɢɬɟɥɶɧɵɯ ɱɢɫɟɥ, ɤɚɠɞɨɟ ɢɡ ɤɨɬɨɪɵɯ ɟɫɬɶ ɫɭɦɦɚ ɞɜɭɯ ɩɨɥɨɠɢɬɟɥɶɧɵɯ ɧɟɱɟɬɧɵɯ ɱɢɫɟɥ. Ⱦɨɤɚɠɟɦ, ɱɬɨ A B.
ɉɪɨɜɟɪɢɦ, ɜɵɩɨɥɧɹɸɬɫɹ ɥɢ ɭɤɚɡɚɧɧɵɟ ɭɫɥɨɜɢɹ:
ɉɭɫɬɶ x A, ɬɨ ɟɫɬɶ x – ɩɨɥɨɠɢɬɟɥɶɧɨɟ ɱɟɬɧɨɟ ɱɢɫɥɨ. ɗɬɨ ɡɧɚɱɢɬ, ɱɬɨ x 2uk, ɝɞɟ k – ɧɟɤɨɬɨɪɨɟ ɧɚɬɭɪɚɥɶɧɨɟ ɱɢɫɥɨ. ɉɪɟɨɛɪɚɡɭɟɦ ɜɵɪɚɠɟɧɢɟ ɞɥɹ x: x (2uk 1) 1, ɬɨ ɟɫɬɶ ɩɪɟɞɫɬɚɜɢɦ x ɫɭɦɦɨɣ ɞɜɭɯ ɩɨɥɨɠɢɬɟɥɶɧɵɯ ɧɟɱɟɬɧɵɯɱɢɫɟɥ2uk 1 ɢ1. Ⱥɷɬɨɨɡɧɚɱɚɟɬ, ɱɬɨx B.
ɉɭɫɬɶ x B, ɬɨ ɟɫɬɶ x m1 m2, ɝɞɟ m1 ɢ m2 – ɩɨɥɨɠɢɬɟɥɶɧɵɟ ɧɟɱɟɬɧɵɟ ɱɢɫɥɚ. Ⱦɥɹ ɧɢɯ ɜɫɟɝɞɚ ɦɨɠɧɨ ɧɚɣɬɢ ɬɚɤɢɟ ɧɚɬɭ-
ɪɚɥɶɧɵɟ ɱɢɫɥɚ |
k1 ɢ k2, ɱɬɨ m1 2uk1 1, ɚ m2 2uk2 1. Ɍɨɝɞɚ |
x 2uk1 1 2uk2 1 |
2u(k1 k2 1) 2uk. |
Ɂɧɚɱɢɬ, x – ɩɨɥɨɠɢɬɟɥɶɧɨɟ ɱɟɬɧɨɟ ɱɢɫɥɨ, ɩɨɫɤɨɥɶɤɭ k k1 k2 1 – ɧɚɬɭɪɚɥɶɧɨɟ ɱɢɫɥɨ. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, x A.
ɂɬɚɤ, ɭɬɜɟɪɠɞɟɧɢɟ A B (ɩɪɢ ɡɚɞɚɧɧɵɯ ɭɫɥɨɜɢɹɯ) ɞɨɤɚɡɚɧɨ. ɍɬɜɟɪɠɞɟɧɢɟ A B ɜɟɪɧɨ ɢ ɬɨɝɞɚ, ɤɨɝɞɚ ɦɟɠɞɭ ɧɢɦɢ ɨɞɧɨɜɪɟɦɟɧ-
ɧɨ ɢɦɟɸɬ ɦɟɫɬɨ ɨɬɧɨɲɟɧɢɹ:
12
|
A B ɢ B A. |
||
|
Ɂɚɞɚɞɢɦ, ɧɚɩɪɢɦɟɪ, ɦɧɨɠɟɫɬɜɨ W ɬɚɤ: |
||
|
W {Ɇ,ɇ,Ɉ,ɀ,ȿ,ɋ,Ɍ,ȼ,Ⱥ}. |
||
ȼɨɬ ɧɟɤɨɬɨɪɵɟ ɢɡ ɟɝɨ ɩɨɞɦɧɨɠɟɫɬɜ: |
|||
|
S1 {ɇ,Ɉ,ɋ}, S2 {ɋ,Ɉ,ɇ}, S3 {Ɇ,Ⱥ,ɇ,ȿ,ɀ}, |
||
|
S4 { Ɇ,Ɉ,ɇ,ȿ,Ɍ,Ⱥ}, S5 {ɀ,ȿ,Ɇ,Ⱥ,ɇ,ɋ,Ɍ,ȼ,Ɉ}. |
||
Ʉɚɤ ɜɢɞɢɦ, S1 S2, ɚ S4 W. Ɍɨɱɧɨ ɬɚɤ S5 W. ȼ ɬɨ ɠɟ ɜɪɟɦɹ ɢ W S5. |
|||
Ɂɧɚɱɢɬ, W S5. |
|
||
|
Ɉɛɵɱɧɨ ɜ ɯɨɞɟ ɢɫɫɥɟɞɨɜɚɧɢɹ ɬɟɯ ɢɥɢ ɢɧɵɯ ɦɧɨɠɟɫɬɜ ɦɨɠɧɨ ɜɜɟ- |
||
ɫɬɢ ɜ ɪɚɫɫɦɨɬɪɟɧɢɟ ɬɚɤɨɟ ɦɧɨɠɟɫɬɜɨ, ɤɨɬɨɪɨɟ ɜɤɥɸɱɚɟɬ ɜ ɫɟɛɹ ɜɫɟ |
|||
ɞɨɩɭɫɬɢɦɵɟ ɜ ɷɬɨɦ ɢɫɫɥɟɞɨɜɚɧɢɢ ɦɧɨɠɟɫɬɜɚ. Ɍɚɤɨɟ ɲɢɪɨɤɨɟ ɦɧɨɠɟ- |
|||
ɫɬɜɨ ɧɚɡɵɜɚɸɬ ɭɧɢɜɟɪɫɚɥɶɧɵɦ ɢ ɨɛɨɡɧɚɱɚɸɬ ɫɢɦɜɨɥɨɦ :. ȼɫɟ |
|||
ɢɫɫɥɟɞɭɟɦɵɟ ɦɧɨɠɟɫɬɜɚ ɹɜɥɹɸɬɫɹ ɩɨɞɦɧɨɠɟɫɬɜɚɦɢ :. ɇɚɩɪɢɦɟɪ, ɩɪɢ |
|||
ɪɚɫɩɪɟɞɟɥɟɧɢɢ ɮɨɧɞɚ ɚɭɞɢɬɨɪɢɣ ɜ ɪɚɫɩɢɫɚɧɢɢ ɡɚɧɹɬɢɣ ɞɥɹ ɩɟɪɜɨɝɨ ɤɭɪ- |
|||
ɫɚ ɨɩɟɪɢɪɭɸɬ ɫ ɝɪɭɩɩɚɦɢ ɢ ɩɨɞɝɪɭɩɩɚɦɢ ɫɬɭɞɟɧɬɨɜ. ȼ ɤɚɱɟɫɬɜɟ ɭɧɢɜɟɪ- |
|||
: |
|
ɫɚɥɶɧɨɝɨ ɦɧɨɠɟɫɬɜɚ ɩɪɢ ɷɬɨɦ ɦɨɠɧɨ ɪɚɫɫɦɚɬɪɢ- |
|
|
ɜɚɬɶɫɚɦɩɟɪɜɵɣɤɭɪɫ. |
||
|
|
Ⱦɥɹ ɩɨɥɧɨɬɵ ɤɚɪɬɢɧɵ ɭɞɨɛɧɨ ɜɜɟɫɬɢ ɜ ɪɚɫ- |
|
A |
B |
ɫɦɨɬɪɟɧɢɟ ɢ ɩɭɫɬɨɟ ɦɧɨɠɟɫɬɜɨ, ɜ ɤɨɬɨɪɨɦ ɧɟɬ |
|
ɧɢ ɨɞɧɨɝɨ ɷɥɟɦɟɧɬɚ ɢ ɤɨɬɨɪɨɟ ɨɛɨɡɧɚɱɚɸɬ ɫɢɦ- |
|||
|
ɚ) |
||
|
|
ɜɨɥɨɦ . |
|
|
A B |
1.2. Ɉɩɟɪɚɰɢɢ ɧɚɞ ɦɧɨɠɟɫɬɜɚɦɢ |
|
|
ȼ ɬɟɨɪɢɢ ɦɧɨɠɟɫɬɜ ɪɚɫɫɦɚɬɪɢɜɚɸɬ ɨɩɟɪɚ- |
||
|
ɛ) |
ɰɢɢ, ɤɨɬɨɪɵɟ ɩɨɡɜɨɥɹɸɬ ɢɡ ɨɞɧɢɯ ɦɧɨɠɟɫɬɜ ɩɨ- |
|
|
|
ɥɭɱɚɬɶ ɞɪɭɝɢɟ. Ɉɩɢɲɟɦ ɷɬɢ ɨɩɟɪɚɰɢɢ. |
|
|
|
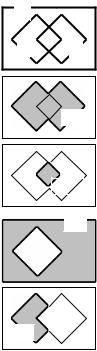
ɉɭɫɬɶ ɡɚɞɚɧɵ ɦɧɨɠɟɫɬɜɚ A, B ɢ : (ɪɢɫ.1.1,ɚ). |
|
A B |
ɜ) |
Ɉɛɴɟɞɢɧɟɧɢɟɦ ɦɧɨɠɟɫɬɜ A ɢ B ɹɜɥɹɟɬɫɹ |
|
ɧɨɜɨɟ ɦɧɨɠɟɫɬɜɨ, ɫɨɫɬɨɹɳɟɟ ɢɡ ɷɥɟɦɟɧɬɨɜ ɦɧɨ- |
|
ºA |
ɠɟɫɬɜɚ A ɢɥɢ ɦɧɨɠɟɫɬɜɚ B (ɪɢɫ.1.1,ɛ). Ɉɛɨɡɧɚ- |
|
|
|
ɱɚɸɬ ɨɩɟɪɚɰɢɸ ɨɛɴɟɞɢɧɟɧɢɹ ɬɚɤ: A B. Ⱦɪɭɝɢɦɢ |
|
|
ɫɥɨɜɚɦɢ: |
ɝ)
A\B
ɞ)
Ɋɢɫ. 1.1
A B {x: x A ɢɥɢ x B}.
ɗɬɚ ɡɚɩɢɫɶ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɦɧɨɠɟɫɬɜɨ A B ɨɛɪɚɡɭɸɬ ɷɥɟɦɟɧɬɵ x, ɚ ɤɚɠɞɵɣ ɢɡ ɧɢɯ ɜɯɨɞɢɬ ɢɥɢ ɜ A, ɢɥɢ ɜ B, ɢɥɢ ɜ ɨɛɚ ɷɬɢ ɦɧɨɠɟɫɬɜɚ. ɇɚɩɪɢɦɟɪ, A {1, 2, 3}, B {1, 3, 4}. Ɍɨɝɞɚ A B {1, 2, 3, 4}. ȼ
ɩɨɫɥɟɞɧɟɦ ɦɧɨɠɟɫɬɜɟ ɷɥɟɦɟɧɬ 2 ɩɪɢɧɚɞɥɟɠɢɬ ɦɧɨɠɟɫɬɜɭ A, ɷɥɟɦɟɧɬ 4 – ɦɧɨɠɟɫɬɜɭ B, ɚ ɷɥɟ-
13

ɦɟɧɬɵ 1 ɢ 3 ɜɯɨɞɹɬ ɢ ɜ A, ɢ ɜ B.
Ɇɨɠɧɨ ɫɨɫɬɚɜɢɬɶ ɨɛɴɟɞɢɧɟɧɢɟ ɥɸɛɨɝɨ ɱɢɫɥɚ ɦɧɨɠɟɫɬɜ:
D A B C.
ɉɟɪɟɫɟɱɟɧɢɟɦ ɦɧɨɠɟɫɬɜ A ɢ B ɧɚɡɵɜɚɸɬ ɧɨɜɨɟ ɦɧɨɠɟɫɬɜɨ, ɤɨɬɨɪɨɟ ɫɨɫɬɨɢɬ ɢɡ ɷɥɟɦɟɧɬɨɜ, ɨɛɳɢɯ ɞɥɹ A ɢ B (ɪɢɫ.1.1,ɜ). ɉɟɪɟɫɟɱɟɧɢɟ ɦɧɨɠɟɫɬɜ A ɢ B ɨɛɨɡɧɚɱɚɸɬ ɤɚɤ A B ɢ ɨɩɪɟɞɟɥɹɸɬ ɡɚɩɢɫɶɸ
A B {x: x A ɢ x B}.
ɗɬɚ ɡɚɩɢɫɶ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɦɧɨɠɟɫɬɜɨ A B ɨɛɪɚɡɭɸɬ ɷɥɟɦɟɧɬɵ x, ɚ ɤɚɠɞɵɣ ɢɡ ɧɢɯ ɜɯɨɞɢɬ ɢ ɜ A, ɢ ɜ B. ɇɚɩɪɢɦɟɪ, ɩɟɪɟɫɟɱɟɧɢɟɦ ɦɧɨɠɟɫɬɜ ɢɡ ɩɪɟɞɵɞɭɳɟɝɨ ɩɪɢɦɟɪɚ ɛɭɞɟɬ ɦɧɨɠɟɫɬɜɨ A B {1, 3}.
Ⱦɜɚ ɦɧɨɠɟɫɬɜɚ A ɢ B ɧɚɡɵɜɚɸɬ ɧɟɩɟɪɟɫɟɤɚɸɳɢɦɢɫɹ, ɟɫɥɢ A B . ȿɫɥɢ ɠɟ A Bz, ɬɨ A ɢ B – ɩɟɪɟɫɟɤɚɸɳɢɟɫɹ ɦɧɨɠɟɫɬɜɚ.
Ɇɨɠɧɨ ɫɨɫɬɚɜɢɬɶ ɩɟɪɟɫɟɱɟɧɢɟ ɥɸɛɨɝɨ ɱɢɫɥɚ ɦɧɨɠɟɫɬɜ:
D A B C.
Ⱦɨɩɨɥɧɟɧɢɟɦ ɦɧɨɠɟɫɬɜɚ A (ɞɨ ɭɧɢɜɟɪɫɚɥɶɧɨɝɨ ɦɧɨɠɟɫɬɜɚ :) ɧɚɡɵɜɚɟɬɫɹ ɧɨɜɨɟ ɦɧɨɠɟɫɬɜɨ ºA (ɢɥɢ A ), ɜɤɥɸɱɚɸɳɟɟ ɜ ɫɟɛɹ ɷɥɟɦɟɧɬɵ ɦɧɨɠɟɫɬɜɚ :, ɧɨɛɟɡɷɥɟɦɟɧɬɨɜɦɧɨɠɟɫɬɜɚ A (ɪɢɫ.1.1,ɝ):
ºA {x: x: ɢ x A}.
ɇɚɩɪɢɦɟɪ:
: {Ⱥɡɢɹ, Ⱥɮɪɢɤɚ, Ⱥɦɟɪɢɤɚ, Ⱥɜɫɬɪɚɥɢɹ, Ⱥɧɬɚɪɤɬɢɞɚ}. A {Ⱥɜɫɬɪɚɥɢɹ, Ⱥɧɬɚɪɤɬɢɞɚ}.
Ɍɨɝɞɚ
ºA º{Ⱥɜɫɬɪɚɥɢɹ, Ⱥɧɬɚɪɤɬɢɞɚ} {Ⱥɡɢɹ, Ⱥɮɪɢɤɚ, Ⱥɦɟɪɢɤɚ}.
Ⱦɨɩɨɥɧɟɧɢɟ – ɨɞɧɨɦɟɫɬɧɚɹ ɨɩɟɪɚɰɢɹ, ɜɵɩɨɥɧɹɟɬɫɹ ɧɚɞ ɨɞɧɢɦ ɦɧɨɠɟɫɬɜɨɦ.
Ɍɟɩɟɪɶ ɦɨɠɧɨ ɫɤɚɡɚɬɶ, ɱɬɨ ɭɧɢɜɟɪɫɚɥɶɧɵɦ ɹɜɥɹɟɬɫɹ ɬɚɤɨɟ ɦɧɨɠɟɫɬɜɨ :, ɞɥɹ ɤɨɬɨɪɨɝɨ ɫɩɪɚɜɟɞɥɢɜɵ ɫɨɨɬɧɨɲɟɧɢɹ:
A: A, A: :.
Ɂɞɟɫɶ A – ɩɪɨɢɡɜɨɥɶɧɨɟ ɦɧɨɠɟɫɬɜɨ.
ȼ ɬɟɨɪɢɢ ɦɧɨɠɟɫɬɜ ɢɫɩɨɥɶɡɭɸɬ ɢ ɞɪɭɝɢɟ ɨɩɟɪɚɰɢɢ. Ɉɞɧɚɤɨ ɬɪɟɯ ɪɚɫɫɦɨɬɪɟɧɧɵɯ ɨɩɟɪɚɰɢɣ ɨɤɚɡɵɜɚɟɬɫɹ ɞɨɫɬɚɬɨɱɧɨ. Ʌɸɛɨɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɟ ɦɧɨɠɟɫɬɜ ɦɨɠɧɨ ɩɪɟɞɫɬɚɜɢɬɶ ɫɭɩɟɪɩɨɡɢɰɢɟɣ ɨɩɟɪɚɰɢɣ ɨɛɴɟɞɢɧɟɧɢɹ, ɩɟɪɟɫɟɱɟɧɢɹ ɢ ɞɨɩɨɥɧɟɧɢɹ.
Ɉɛɴɟɞɢɧɟɧɢɟ, ɩɟɪɟɫɟɱɟɧɢɟ ɦɧɨɠɟɫɬɜ, ɞɨɩɨɥɧɟɧɢɟ ɦɧɨɠɟɫɬɜɚ ɞɨ ɭɧɢɜɟɪɫɚɥɶɧɨɝɨ ɨɛɪɚɡɭɸɬ ɮɭɧɤɰɢɨɧɚɥɶɧɨ ɩɨɥɧɭɸ ɫɢɫɬɟɦɭ ɨɩɟɪɚɰɢɣ ɚɥɝɟɛɪɵ ɦɧɨɠɟɫɬɜ.
14

ɉɪɢ ɩɨɫɬɪɨɟɧɢɢ ɫɭɩɟɪɩɨɡɢɰɢɣ ɧɚɡɜɚɧɧɵɯ ɨɩɟɪɚɰɢɣ ɫɥɟɞɭɟɬ ɭɱɢɬɵɜɚɬɶ ɩɪɚɜɢɥɨ ɨ ɩɪɢɨɪɢɬɟɬɚɯ: ɧɚɢɜɵɫɲɢɦ ɩɪɢɨɪɢɬɟɬɨɦ ɨɛɥɚɞɚɟɬ ɞɨɩɨɥɧɟɧɢɟ, ɫɥɟɞɭɸɳɢɣ ɩɪɢɨɪɢɬɟɬ – ɭ ɩɟɪɟɫɟɱɟɧɢɹ, ɫɚɦɵɣ ɧɢɡɤɢɣ ɩɪɢɨɪɢɬɟɬ – ɭ ɨɛɴɟɞɢɧɟɧɢɹ. ɇɚɪɭɲɢɬɶ ɩɪɚɜɢɥɨ ɨ ɩɪɢɨɪɢɬɟɬɚɯ ɢ ɡɚɞɚɬɶ ɢɧɨɣ ɩɨɪɹɞɨɤ ɜɵɩɨɥɧɟɧɢɹ ɨɩɟɪɚɰɢɣ ɩɨɡɜɨɥɹɸɬ ɫɤɨɛɤɢ. ȼɵɪɚɠɟɧɢɟ ɜ ɫɤɨɛɤɚɯ ɪɟɚɥɢɡɭɟɬɫɹ ɜ ɩɟɪɜɭɸ ɨɱɟɪɟɞɶ.
ɇɚɩɪɢɦɟɪ, ɪɚɡɧɨɫɬɶɸ ɦɧɨɠɟɫɬɜ A ɢ B ɧɚɡɵɜɚɸɬ ɦɧɨɠɟɫɬɜɨ A\B, ɜ
ɤɨɬɨɪɨɟ ɜɤɥɸɱɟɧɵ ɷɥɟɦɟɧɬɵ ɦɧɨɠɟɫɬɜɚ A ɢ ɧɟ ɜɤɥɸɱɟɧɵ ɷɥɟɦɟɧɬɵ ɦɧɨɠɟɫɬɜɚ B (ɪɢɫ.1.1,ɞ), ɬɨ ɟɫɬɶ
A\B {x: x A ɢ x B}.
ȼɵɪɚɡɢɦ ɨɩɟɪɚɰɢɸ A\B ɜ ɬɟɪɦɢɧɚɯ ɮɭɧɤɰɢɨɧɚɥɶɧɨ ɩɨɥɧɨɣ ɫɢɫɬɟɦɵ ɨɩɟɪɚɰɢɣ:
A\B AºB. |
(1.1) |
ɂɧɨɝɞɚ ɭɞɨɛɧɨ ɛɵɜɚɟɬ ɩɪɟɞɫɬɚɜɢɬɶ ɞɨɩɨɥɧɟɧɢɟ ɦɧɨɠɟɫɬɜɚ A ɞɨ ɭɧɢɜɟɪɫɚɥɶɧɨɝɨ ɬɚɤɨɣ ɪɚɡɧɨɫɬɶɸ:
ºA :\A.
Ɉɬɦɟɬɢɦ, ɱɬɨ ɩɨɫɥɟ ɜɵɩɨɥɧɟɧɢɹ ɬɨɣ ɢɥɢ ɢɧɨɣ ɨɩɟɪɚɰɢɢ ɧɚɞ ɡɚɞɚɧɧɵɦɢ ɦɧɨɠɟɫɬɜɚɦɢ ɨɫɬɚɟɬɫɹ ɬɨɥɶɤɨ ɪɟɡɭɥɶɬɚɬ ɨɩɟɪɚɰɢɢ – ɧɨɜɨɟ ɦɧɨɠɟɫɬɜɨ (ɪɢɫ. 1.1).
1.3. Ⱥɤɫɢɨɦɵ ɢ ɬɟɨɪɟɦɵ ɚɥɝɟɛɪɵ ɦɧɨɠɟɫɬɜ
Ⱦɥɹ ɥɸɛɵɯ ɦɧɨɠɟɫɬɜ A, B ɢ C ɫɩɪɚɜɟɞɥɢɜɵ ɫɥɟɞɭɸɳɢɟ ɚɤɫɢɨɦɵ ɢ ɬɟɨɪɟɦɵ (ɬɚɛɥ. 1.1). Ɂɞɟɫɶ ɭɬɜɟɪɠɞɟɧɢɹ 1..5 ɢ 1’..5’ – ɚɤɫɢɨɦɵ ɚɥɝɟɛɪɵ ɦɧɨɠɟɫɬɜ, ɨɫɬɚɥɶɧɵɟ ɭɬɜɟɪɠɞɟɧɢɹ – ɧɟɤɨɬɨɪɵɟ ɢɡ ɨɫɧɨɜɧɵɯ ɟɟ ɬɟɨɪɟɦ. ɂ ɬɟ, ɢ ɞɪɭɝɢɟ ɨɛɴɟɞɢɧɢɦ ɨɞɧɢɦ ɫɥɨɜɨɦ – ɬɨɠɞɟɫɬɜɚ.
|
|
|
|
|
|
|
|
|
|
Ɍɚɛɥɢɰɚ 1.1 |
1 |
|
A B B A |
|
5 |
|
AºA : |
|
|
9 |
(A B) (AºB) A |
|
1’ |
A B B A |
|
|
5’ |
AºA |
|
|
9’ |
(A B) (AºB) A |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
A B C A (B C) |
|
6 |
|
A: : |
|
|
10 |
º(A B) ºAºB |
|
2’ |
A B C A (B C) |
|
|
6’ |
A |
|
|
10’ |
º(A B) ºAºB |
|
|
|
|
|
|
|
|
|||
3 |
|
A (B C) (A B) (A C) |
|
7 |
|
A A A |
|
11 |
º: |
|
|
3’ |
A (B C) (A B) (A C) |
|
|
7’ |
A A A |
|
|
11’ |
º : |
|
|
|
|
|
|
|
|
|||
4 |
|
A A |
|
8 |
|
A (A B) A |
|
12 |
ººA A |
|
|
4’ |
A: A |
|
|
8’ |
A (A B) A |
|
|
|
|
15

ɍɤɚɠɟɦ ɧɚ ɢɡɜɟɫɬɧɭɸ ɚɧɚɥɨɝɢɸ ɦɟɠɞɭ ɩɪɢɜɟɞɟɧɧɵɦɢ ɚɤɫɢɨɦɚɦɢ ɚɥɝɟɛɪɵ ɦɧɨɠɟɫɬɜ ɢ ɚɤɫɢɨɦɚɦɢ ɲɤɨɥɶɧɨɣ ɚɥɝɟɛɪɵ. Ɍɚɤ, ɜ ɬɟɨɪɢɢ ɦɧɨɠɟɫɬɜ ɚɤɫɢɨɦɵ 1 ɢ 1’ ɧɚɡɵɜɚɸɬɫɹ ɤɨɦɦɭɬɚɬɢɜɧɵɦɢ ɡɚɤɨɧɚɦɢ. ɗɬɢ ɡɚɤɨɧɵ ɭɬɜɟɪɠɞɚɸɬ, ɱɬɨ ɜ ɨɩɟɪɚɰɢɹɯ ɨɛɴɟɞɢɧɟɧɢɹ ɢ ɩɟɪɟɫɟɱɟɧɢɹ ɨɩɟɪɚɧɞɵ ɦɨɠɧɨ ɪɚɫɩɨɥɚɝɚɬɶ ɜ ɥɸɛɨɦ ɩɨɪɹɞɤɟ. Ⱥɤɫɢɨɦɵ 2 ɢ 2’ – ɷɬɨ ɚɫɫɨɰɢɚɬɢɜɧɵɟ ɡɚɤɨɧɵ ɞɥɹ ɦɧɨɠɟɫɬɜ. Ɉɧɢ ɫɜɢɞɟɬɟɥɶɫɬɜɭɸɬ ɨ ɬɨɦ, ɱɬɨ ɤɚɠɞɭɸ ɢɡ ɦɧɨɝɨɦɟɫɬɧɵɯ ɨɩɟɪɚɰɢɣ ɧɚɞ ɦɧɨɠɟɫɬɜɚɦɢ ɦɨɠɧɨ ɫɜɟɫɬɢ ɤ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɫɬɢ ɞɜɭɦɟɫɬɧɵɯ ɨɩɟɪɚɰɢɣ. Ⱥɤɫɢɨɦɟ 3’ ɜ ɲɤɨɥɶɧɨɣ ɚɥɝɟɛɪɟ ɨɬɜɟɱɚɟɬ ɞɢɫɬɪɢɛɭɬɢɜɧɵɣ ɡɚɤɨɧ. Ⱥ ɜɨɬ ɚɤɫɢɨɦɟ 3 ɜ ɲɤɨɥɶɧɨɣ ɚɥɝɟɛɪɟ ɧɟɬ ɚɧɚɥɨɝɚ. Ɍɟɦ ɧɟ ɦɟɧɟɟ ɚɤɫɢɨɦɵ 3 ɢ 3’ ɚɥɝɟɛɪɵ ɦɧɨɠɟɫɬɜ ɧɚɡɵɜɚɸɬɫɹ ɞɢɫɬɪɢɛɭɬɢɜɧɵɦɢ ɡɚɤɨɧɚɦɢ ɞɥɹ ɦɧɨɠɟɫɬɜ. ɗɬɢ ɡɚɤɨɧɵ ɡɚɞɚɸɬ ɩɪɚɜɢɥɚ ɪɚɫɤɪɵɬɢɹ ɫɤɨɛɨɤ (ɟɫɥɢ ɞɜɢɝɚɬɶɫɹ ɨɬ ɥɟɜɨɣ ɱɚɫɬɢ ɪɚɜɟɧɫɬɜɚ ɤ ɟɝɨ ɩɪɚɜɨɣ ɱɚɫɬɢ) ɢɥɢ ɠɟ ɩɪɚɜɢɥɨ ɜɵɧɨɫɚ ɡɚ ɫɤɨɛɤɢ ɩɨɞɨɛɧɵɯ ɱɥɟɧɨɜ (ɟɫɥɢ ɞɜɢɝɚɬɶɫɹ ɜ ɨɛɪɚɬɧɨɦ ɧɚɩɪɚɜɥɟɧɢɢ).
Ɉɛɪɚɬɢɦ ɜɧɢɦɚɧɢɟ ɧɚ ɩɚɪɧɵɟ ɭɬɜɟɪɠɞɟɧɢɹ ɬɚɛɥ. 1.1. Ɍɨɠɞɟɫɬ-
ɜɨ ɧɨɦɟɪ J’ ɩɨɥɭɱɚɸɬ ɢɡ ɩɚɪɧɨɝɨ ɬɨɠɞɟɫɬɜɚ ɧɨɦɟɪ J (J 1,11) ɩɭɬɟɦ ɡɚɦɟɧɵ ɜ ɧɟɦ ɫɢɦɜɨɥɚ ɧɚ ɫɢɦɜɨɥ ɢ ɧɚɨɛɨɪɨɬ, ɫɢɦɜɨɥɚ : ɧɚ ɫɢɦɜɨɥ ɢ ɧɚɨɛɨɪɨɬ. Ƚɨɜɨɪɹɬ, ɱɬɨ ɬɨɠɞɟɫɬɜɚ J ɢ J’ ɞɜɨɣɫɬɜɟɧɧɵ (ɞɭɚɥɶɧɵ) ɞɪɭɝ ɞɪɭɝɭ.
Ⱦɥɹ ɥɸɛɵɯ ɞɭɚɥɶɧɵɯ ɜɵɪɚɠɟɧɢɣ ɫɩɪɚɜɟɞɥɢɜɨ ɭɬɜɟɪɠɞɟɧɢɟ: ɟɫɥɢ ɜɵɪɚɠɟɧɢɟ J ɜɟɪɧɨ, ɬɨ ɜɟɪɧɨ ɢ ɞɜɨɣɫɬɜɟɧɧɨɟ ɟɦɭ ɜɵɪɚɠɟɧɢɟ J’. ɉɨɷɬɨɦɭ ɧɟɬ ɧɭɠɞɵ ɞɨɤɚɡɵɜɚɬɶ ɜɟɪɧɨɫɬɶ ɤɚɠɞɨɝɨ ɢɡ ɞɭɚɥɶɧɵɯ ɜɵɪɚɠɟɧɢɣ, ɞɨɫɬɚɬɨɱɧɨ ɞɨɤɚɡɚɬɶ ɥɢɲɶ ɨɞɧɨ ɢɡ ɧɢɯ. ɗɬɨ ɭɬɜɟɪɠɞɟɧɢɟ ɧɚɡɵɜɚɸɬ ɩɪɢɧɰɢɩɨɦ ɞɜɨɣɫɬɜɟɧɧɨɫɬɢ.
Ɋɚɞɢ ɩɨɥɧɨɣ ɫɢɦɦɟɬɪɢɢ ɜ ɜɵɪɚɠɟɧɢɹɯ 1..10 ɢ 1’..10’ ɫɤɨɛɤɢ ɩɪɨɫɬɚɜɥɟɧɵ ɢ ɬɚɦ, ɝɞɟ ɛɟɡ ɧɢɯ ɦɨɠɧɨ ɛɵɥɨ ɛɵ ɨɛɨɣɬɢɫɶ ɩɨ ɩɪɚɜɢɥɭ ɨ ɩɪɢɨɪɢɬɟɬɚɯ.
Ⱥɤɫɢɨɦɵ 1..5 ɢ 1’..5’ ɫɪɟɞɫɬɜɚɦɢ ɬɟɨɪɢɢ ɦɧɨɠɟɫɬɜ ɧɟ ɞɨɤɚɡɵɜɚɸɬɫɹ, ɧɨ ɩɨɞɬɜɟɪɠɞɚɸɬɫɹ ɩɪɨɜɟɪɤɨɣ. ɉɪɨɜɟɪɢɦ, ɧɚɩɪɢɦɟɪ, ɜɟɪɧɨɫɬɶ ɭɬɜɟɪɠɞɟɧɢɹ 3. Ɉɬɩɪɚɜɥɹɟɦɫɹ ɨɬ ɟɝɨ ɥɟɜɨɣ ɱɚɫɬɢ. ɉɭɫɬɶ x A (B C). Ɍɨɝɞɚ ɩɨ ɨɩɪɟɞɟɥɟɧɢɸ ɞɥɹ ɨɛɴɟɞɢɧɟɧɢɹ ɢɦɟɟɦ x A ɢɥɢ x (B C). ɇɨ ɟɫɥɢ x A, ɬɨ x ɩɪɢɧɚɞɥɟɠɢɬ ɢ ɨɛɴɟɞɢɧɟɧɢɸ A ɫ ɥɸɛɵɦ ɞɪɭɝɢɦ ɦɧɨɠɟɫɬɜɨɦ. ȼ ɱɚɫɬɧɨɫɬɢ x A B ɢ x A C. Ɂɧɚɱɢɬ, x ɩɪɢɧɚɞɥɟɠɢɬ ɩɟɪɟɫɟɱɟɧɢɸ ɷɬɢɯ ɦɧɨɠɟɫɬɜ, ɬɨ ɟɫɬɶ x (A B) (A C), ɚ ɷɬɨ – ɩɪɚɜɚɹ ɱɚɫɬɶ ɭɬɜɟɪɠɞɟɧɢɹ 3. Ⱥ ɟɫɥɢ x (B C), ɬɨ ɢɡ ɨɩɪɟɞɟɥɟɧɢɹ ɞɥɹ ɩɟɪɟɫɟɱɟɧɢɹ ɦɧɨɠɟɫɬɜ ɜɵɬɟɤɚɟɬ, ɱɬɨ x B ɢ x C. Ɂɧɚɱɢɬ, x ɩɪɢɧɚɞɥɟɠɢɬ ɢ ɨɛɴɟɞɢɧɟɧɢɸ ɤɚɠɞɨɝɨ ɢɡ ɦɧɨɠɟɫɬɜ B ɢ C ɫ ɥɸɛɵɦ ɞɪɭɝɢɦ ɦɧɨɠɟɫɬɜɨɦ, ɜ ɱɚɫɬɧɨɫɬɢ ɫ A: x (A B) ɢ x (A C). Ɍɨɝɞɚ ɫɧɨɜɚ ɢɦɟɟɦ x (A B) (A C). Ɍɚɤ, ɞɜɢɝɚɹɫɶ ɨɬ ɥɟɜɨɣ ɱɚɫɬɢ 3, ɩɪɢɯɨɞɢɦ ɤ ɟɝɨ ɩɪɚɜɨɣ ɱɚɫɬɢ. Ⱥɧɚɥɨɝɢɱɧɨ, ɞɜɢɝɚɹɫɶ ɨɬ ɩɪɚɜɨɣ ɱɚɫɬɢ 3, ɦɨɠɧɨ ɩɪɢɣɬɢ ɤ ɟɝɨ ɥɟɜɨɣ ɱɚɫɬɢ. ɉɨɫɤɨɥɶɤɭ ɭɬɜɟɪɠɞɟɧɢɟ 3 ɜɟɪɧɨ, ɜɟɪɧɨ ɢ ɭɬɜɟɪɠɞɟɧɢɟ 3’.
16

Ɍɨɠɞɟɫɬɜɚ 1..11, 1’..11’ ɢ 12 ɢɫɩɨɥɶɡɭɸɬ ɞɥɹ ɞɨɤɚɡɚɬɟɥɶɫɬɜɚ ɬɟɯ ɢɥɢ ɢɧɵɯ ɭɬɜɟɪɠɞɟɧɢɣ ɨɬɧɨɫɢɬɟɥɶɧɨ ɦɧɨɠɟɫɬɜ, ɞɥɹ ɭɩɪɨɳɟɧɢɹ ɜɵɪɚɠɟɧɢɣ ɚɥɝɟɛɪɵɦɧɨɠɟɫɬɜ. Ⱦɨɤɚɠɟɦ, ɤɩɪɢɦɟɪɭ, ɫɥɟɞɭɸɳɟɟɭɬɜɟɪɠɞɟɧɢɟ:
ɟɫɥɢ A B : ɢ A B , ɬɨ B ºA.
ɇɨɦɟɪɚ ɬɨɠɞɟɫɬɜ, ɤɨɬɨɪɵɟ ɢɫɩɨɥɶɡɭɸɬɫɹ ɜ ɰɟɩɨɱɤɟ ɧɚɲɢɯ ɪɚɫɫɭɠɞɟɧɢɣ, ɛɭɞɟɦ ɡɚɤɥɸɱɚɬɶ ɜ ɭɝɥɨɜɵɟ ɫɤɨɛɤɢ. ɂɬɚɤ,
B¢4² B ¢5’² B (A ºA) ¢3² (B A) (B ºA)
¢1 ɢ ɭɫɥɨɜɢɟ A B :² : (B ºA) ¢5² (A ºA) (B ºA) ¢1² (ºA A) (ºA B) ¢3²
ºA (A B) ¢ɭɫɥɨɜɢɟ A B ² ºA ¢4² ºA,
ɱɬɨ ɢ ɬɪɟɛɨɜɚɥɨɫɶ ɞɨɤɚɡɚɬɶ. ɑɢɬɚɬɟɥɸ ɩɪɟɞɥɨɠɢɦ ɩɪɨɢɥɥɸɫɬɪɢɪɨɜɚɬɶ ɧɚɲɢ ɪɚɫɫɭɠɞɟɧɢɹ ɪɢɫɭɧɤɨɦ.
ȼɨɩɪɨɫɵ ɢ ɡɚɞɚɱɢ ɞɥɹ ɫɚɦɨɤɨɧɬɪɨɥɹ
1.ɉɨɹɫɧɢɬɟ ɩɨɧɹɬɢɟ ɦɧɨɠɟɫɬɜɚ, ɤɚɤɢɟ ɨɬɧɨɲɟɧɢɹ ɛɵɜɚɸɬ ɦɟɠɞɭ ɦɧɨɠɟɫɬɜɚɦɢ. Ⱦɚɣɬɟ ɨɩɪɟɞɟɥɟɧɢɟ ɭɧɢɜɟɪɫɚɥɶɧɨɝɨ ɦɧɨɠɟɫɬɜɚ.
2.ɉɨɹɫɧɢɬɟ ɫɦɵɫɥ ɨɩɟɪɚɰɢɣ ɚɥɝɟɛɪɵ ɦɧɨɠɟɫɬɜ:
ɨɛɴɟɞɢɧɟɧɢɟ ɦɧɨɠɟɫɬɜ,
ɩɟɪɟɫɟɱɟɧɢɟ ɦɧɨɠɟɫɬɜ,
ɞɨɩɨɥɧɟɧɢɟ ɦɧɨɠɟɫɬɜɚ ɞɨ ɭɧɢɜɟɪɫɚɥɶɧɨɝɨ.
3.ɉɨɹɫɧɢɬɟ ɨɫɧɨɜɧɨɟ ɫɜɨɣɫɬɜɨ ɮɭɧɤɰɢɨɧɚɥɶɧɨ ɩɨɥɧɨɣ ɫɢɫɬɟɦɵ ɨɩɟɪɚɰɢɣ ɚɥɝɟɛɪɵ ɦɧɨɠɟɫɬɜ.
4.Ⱦɨɤɚɡɚɬɶ ɭɬɜɟɪɠɞɟɧɢɹ ɚɥɝɟɛɪɵ ɦɧɨɠɟɫɬɜ:
ɚ) A (ºA B) A B, ɛ) (A B) (A ºB) A, |
|
: |
|
|
|
|
|
|
|
|
3 |
|
|
||||
|
|
|
B |
|
|
|||
|
|
|
|
|
||||
ɜ) º(A B) (ºA ºB), ɝ) º(A B) (ºA ºB). |
|
|
|
|
|
|||
|
|
|
C |
|||||
|
|
|
|
|
||||
5. ɍɧɢɜɟɪɫɚɥɶɧɨɟ ɦɧɨɠɟɫɬɜɨ : ɟɝɨ ɩɨɞɦɧɨɠɟɫɬ- |
4 |
5 |
|
|
||||
|
|
|||||||
|
|
|
|
6 8 7 |
|
|
||
ɜɚɦɢA, B, C ɪɚɡɛɢɜɚɟɬɫɹɧɚɜɨɫɟɦɶɧɟɩɟɪɟɫɟɤɚɸɳɢɯɫɹ |
1 |
|
|
|
|
|||
ɨɛɥɚɫɬɟɣ 1..8 (ɪɢɫ.1.2). Ʉɚɠɞɭɸ ɢɡ ɷɬɢɯ ɨɛɥɚɫɬɟɣ ɨɩɢ- |
|
|
|
2 |
|
|
||
A |
|
|
|
|||||
ɫɚɬɶɜɬɟɪɦɢɧɚɯɨɩɟɪɚɰɢɣɚɥɝɟɛɪɵɦɧɨɠɟɫɬɜ. |
|
|
|
|
|
|
|
|
6. ɇɚ ɪɢɫ. 1.2 ɭɛɪɚɬɶ ɜɫɟ ɧɨɦɟɪɚ ɢ ɡɚɲɬɪɢɯɨ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɜɚɬɶ ɤɚɠɞɭɸ ɢɡ ɨɛɥɚɫɬɟɣ, ɤɨɬɨɪɵɟ ɨɩɪɟɞɟɥɹɸɬɫɹ |
|
|
|
Ɋɢɫ. 1.2 |
|
|
||
ɫɨɨɬɧɨɲɟɧɢɹɦɢ: |
|
|
|
|
|
|
|
|
ɚ) º(A B C), ɛ) º(A B C), ɜ) A º(B C), ɝ) º(A (B C)).
7. ɋɨɫɬɚɜɥɟɧɵ ɞɜɚ ɫɩɢɫɤɚ ɩɪɚɜɨɜɵɯ ɞɨɤɭɦɟɧɬɨɜ ɩɨ ɩɪɨɛɥɟɦɟ «ɂɧɮɨɪɦɚɰɢɨɧɧɚɹ ɛɟɡɨɩɚɫɧɨɫɬɶ» (ɫɩɢɫɨɤ ɂȻ) ɢ ɩɨ ɩɪɨɛɥɟɦɟ «Ɂɚɳɢɬɚ ɢɧɮɨɪɦɚɰɢɢ» (ɫɩɢɫɨɤ Ɂɂ). Ɂɚɩɢɫɚɬɶ ɬɟ ɨɩɟɪɚɰɢɢ ɧɚɞ ɦɧɨɠɟɫɬɜɚɦɢ ɂȻ ɢ Ɂɂ, ɤɨɬɨɪɵɟ ɩɨɡɜɨɥɹɬ:
ɚ) ɜɵɞɟɥɢɬɶ ɞɨɤɭɦɟɧɬɵ, ɜɤɥɸɱɟɧɧɵɟ ɢ ɜ ɫɩɢɫɨɤ ɂȻ, ɢ ɜ
ɫɩɢɫɨɤ Ɂɂ,
17
ɛ) ɜɵɞɟɥɢɬɶ ɞɨɤɭɦɟɧɬɵ, ɜɤɥɸɱɟɧɧɵɟ ɬɨɥɶɤɨ ɜ ɫɩɢɫɨɤ ɂȻ, ɜ) ɜɵɞɟɥɢɬɶ ɞɨɤɭɦɟɧɬɵ, ɜɤɥɸɱɟɧɧɵɟ ɬɨɥɶɤɨ ɜ ɫɩɢɫɨɤ Ɂɂ, ɝ) ɫɨɫɬɚɜɢɬɶ ɩɨɥɧɵɣ ɩɟɪɟɱɟɧɶ ɞɨɤɭɦɟɧɬɨɜ (ɛɟɡ ɩɨɜɬɨɪɨɜ).
Глава 2. Элементы математической логики
2.1. Начала алгебры высказываний
Ɇɚɬɟɦɚɬɢɱɟɫɤɚɹ ɥɨɝɢɤɚ – ɷɬɨ ɬɟɨɪɢɹ ɜɟɪɧɵɯ ɪɚɫɫɭɠɞɟɧɢɣ. ɉɪɢ ɷɬɨɦ ɚɛɫɨɥɸɬɧɨ ɛɟɡɪɚɡɥɢɱɧɨ, ɤ ɤɚɤɨɣ ɨɛɥɚɫɬɢ ɷɬɢ ɪɚɫɫɭɠɞɟɧɢɹ ɨɬɧɨɫɹɬɫɹ. ɐɟɩɨɱɤɚ ɪɚɫɫɭɠɞɟɧɢɣ, ɨɬɧɨɫɹɳɢɯɫɹ ɤ ɬɨɣ ɢɥɢ ɢɧɨɣ ɨɛɥɚɫɬɢ, ɨɩɢɫɵɜɚɟɬɫɹ ɧɚ ɹɡɵɤɟ ɦɚɬɟɦɚɬɢɱɟɫɤɨɣ (ɮɨɪɦɚɥɶɧɨɣ) ɥɨɝɢɤɢ, ɚ ɡɚɬɟɦ ɩɪɨɜɟɪɹɟɬɫɹ ɢɯ ɜɟɪɧɨɫɬɶ ɢɥɢ ɨɲɢɛɨɱɧɨɫɬɶ. Ɍɚɤɚɹ ɭɧɢɜɟɪɫɚɥɶɧɨɫɬɶ ɡɚɤɨɧɨɜ ɦɚɬɟɦɚɬɢɱɟɫɤɨɣ ɥɨɝɢɤɢ ɨɛɭɫɥɨɜɢɥɚ ɟɟ ɲɢɪɨɤɨɟ ɩɪɢɦɟɧɟɧɢɟ ɤɚɤ ɜ ɬɟɯɧɢɱɟɫɤɢɯ, ɬɚɤ ɢ ɜ ɝɭɦɚɧɢɬɚɪɧɵɯ ɧɚɭɤɚɯ. Ɉɧɚ ɫɨɫɬɚɜɥɹɟɬ ɬɟɨɪɟɬɢɱɟɫɤɢɣ ɮɭɧɞɚɦɟɧɬ ɩɨɫɬɪɨɟɧɢɹ ɢ ɮɭɧɤɰɢɨɧɢɪɨɜɚɧɢɹ ɤɨɦɩɶɸɬɟɪɨɜ, ɟɟ ɦɟɬɨɞɵ ɚɤɬɢɜɧɨ ɢɫɩɨɥɶɡɭɸɬɫɹ ɜ ɷɤɨɧɨɦɢɤɟ, ɦɟɞɢɰɢɧɟ, ɩɫɢɯɨɥɨɝɢɢ, ɹɡɵɤɨɡɧɚɧɢɢ ɢ ɞɪ.
Ɉɫɧɨɜɧɨɟ ɩɨɧɹɬɢɟ ɦɚɬɟɦɚɬɢɱɟɫɤɨɣ ɥɨɝɢɤɢ – ɜɵɫɤɚɡɵɜɚɧɢɟ (ɭɬɜɟɪɠɞɟɧɢɟ). ɗɬɨ ɩɨɧɹɬɢɟ ɫɪɟɞɫɬɜɚɦɢ ɦɚɬɟɦɚɬɢɱɟɫɤɨɣ ɥɨɝɢɤɢ ɧɟ ɨɩɪɟɞɟɥɹɟɬɫɹ. Ɉɫɧɨɜɧɨɣ ɩɪɢɡɧɚɤ ɜɵɫɤɚɡɵɜɚɧɢɹ: ɨɧɨ ɦɨɠɟɬ ɛɵɬɶ ɢɥɢ ɢɫɬɢɧɧɵɦ, ɢɥɢ ɥɨɠɧɵɦ. ɉɪɢ ɷɬɨɦ ɜɵɫɤɚɡɵɜɚɧɢɟ ɧɟ ɦɨɠɟɬ ɛɵɬɶ ɢ ɢɫɬɢɧɧɵɦ, ɢ ɥɨɠɧɵɦ ɨɞɧɨɜɪɟɦɟɧɧɨ. Ƚɨɜɨɪɹɬ, ɱɬɨ ɢɫɬɢɧɚ ɢɥɢ ɥɨɠɶ – ɜɨɡɦɨɠɧɵɟ ɡɧɚɱɟɧɢɹ ɤɚɠɞɨɝɨ ɢɡ ɜɵɫɤɚɡɵɜɚɧɢɣ. ɋɨɞɟɪɠɚɧɢɟ ɜɵɫɤɚɡɵɜɚɧɢɹ ɧɟɫɭɳɟɫɬɜɟɧɧɨ. Ⱦɥɹ ɩɪɢɦɟɪɚ ɩɪɢɜɟɞɟɦ ɬɚɤɢɟ ɜɵɫɤɚɡɵɜɚɧɢɹ ɢɡ ɪɚɡɧɵɯ ɨɛɥɚɫɬɟɣ:
1)Ɇɚɬɟɦɚɬɢɤɚ – ɷɬɨ ɤɪɭɬɨ!
2)H2O – ɮɨɪɦɭɥɚ ɷɬɢɥɨɜɨɝɨ ɫɩɢɪɬɚ.
3)ȿɫɥɢ 25 ɢ 3 ɫɭɬɶ ɜɨɫɶɦɟɪɢɱɧɵɟ ɱɢɫɥɚ, ɬɨ 25 ɞɟɥɢɬɫɹ ɧɚ 3.
ɇɟ ɹɜɥɹɸɬɫɹ ɜɵɫɤɚɡɵɜɚɧɢɹɦɢ ɮɪɚɡɵ ɬɢɩɚ: «Ʌɸɛɨɜɶ ɟɫɬɶ ɩɪɟɞɢɫɥɨɜɢɟ ɤ ɪɚɡɥɭɤɟ» (ɂ. Ȼɪɨɞɫɤɢɣ), «Ɂɪɢ ɜ ɤɨɪɟɧɶ!» (Ʉɨɡɶɦɚ ɉɪɭɬɤɨɜ), «Ɋɚɡɪɟɲɢɬɟ ɜɵɣɬɢ?»(ɫɬɭɞɟɧɬ ɩɟɪɜɨɝɨ ɤɭɪɫɚ). ɉɪɨ ɤɚɠɞɭɸ ɢɡ ɧɢɯ ɧɟɥɶɡɹ ɫɤɚɡɚɬɶ, ɢɫɬɢɧɧɚ ɨɧɚ ɢɥɢ ɥɨɠɧɚ.
Ɉɱɟɜɢɞɧɨ, ɱɬɨ ɫɭɳɟɫɬɜɭɸɬ ɜɵɫɤɚɡɵɜɚɧɢɹ ɩɪɨɫɬɵɟ ɢ ɫɥɨɠɧɵɟ. ɋɥɨɠɧɨɟ ɜɵɫɤɚɡɵɜɚɧɢɟ ɦɨɠɧɨ ɪɚɡɥɨɠɢɬɶ ɧɚ ɩɪɨɫɬɵɟ. ɂɡ ɩɪɢɜɟɞɟɧɧɵɯ ɜɵɲɟ ɜɵɫɤɚɡɵɜɚɧɢɣ ɩɟɪɜɵɟ ɞɜɚ – ɩɪɨɫɬɵɟ, ɚ ɬɪɟɬɶɟ ɫɨɫɬɨɢɬ ɢɡ ɞɜɭɯ ɩɪɨɫɬɵɯ ɜɵɫɤɚɡɵɜɚɧɢɣ: 25 ɢ 3 ɫɭɬɶ ɜɨɫɶɦɟɪɢɱɧɵɟ ɱɢɫɥɚ ɢ 25 ɞɟɥɢɬɫɹ ɧɚ 3.
ɉɪɨɫɬɵɦ ɧɚɡɵɜɚɸɬ ɬɚɤɨɟ ɜɵɫɤɚɡɵɜɚɧɢɟ, ɧɢɤɚɤɚɹ ɱɚɫɬɶ ɤɨɬɨɪɨɝɨ ɜɵɫɤɚɡɵɜɚɧɢɟɦ ɭɠɟ ɧɟ ɹɜɥɹɟɬɫɹ.
ȼɨɬ ɟɳɟ ɩɪɢɦɟɪ ɫɥɨɠɧɨɝɨ ɜɵɫɤɚɡɵɜɚɧɢɹ:
18

«ɉɪɟɫɬɭɩɥɟɧɢɟ ɩɪɢɡɧɚɟɬɫɹ ɫɨɜɟɪɲɟɧɧɵɦ ɫ ɩɪɹɦɵɦ ɭɦɵɫɥɨɦ, ɟɫɥɢ ɥɢɰɨ ɨɫɨɡɧɚɜɚɥɨ ɨɛɳɟɫɬɜɟɧɧɭɸ ɨɩɚɫɧɨɫɬɶ ɫɜɨɢɯ ɞɟɣɫɬɜɢɣ (ɛɟɡɞɟɣɫɬɜɢɹ), ɩɪɟɞɜɢɞɟɥɨ ɜɨɡɦɨɠɧɨɫɬɶ ɢɥɢ ɧɟɢɡɛɟɠɧɨɫɬɶ ɧɚɫɬɭɩɥɟɧɢɹ ɨɛɳɟɫɬɜɟɧɧɨ ɨɩɚɫɧɵɯ ɩɨɫɥɟɞɫɬɜɢɣ ɢ ɠɟɥɚɥɨ ɢɯ ɧɚɫɬɭɩɥɟɧɢɹ» (ɍɄ ɊɎ, ɫɬ. 25, ɱ. 2).
ɉɪɨɫɬɵɟ ɜɵɫɤɚɡɵɜɚɧɢɹ ɜ ɧɟɦ:
ɩɪɟɫɬɭɩɥɟɧɢɟɩɪɢɡɧɚɟɬɫɹɫɨɜɟɪɲɟɧɧɵɦɫɩɪɹɦɵɦɭɦɵɫɥɨɦ,
ɥɢɰɨ ɨɫɨɡɧɚɜɚɥɨ ɨɛɳɟɫɬɜɟɧɧɭɸ ɨɩɚɫɧɨɫɬɶ ɫɜɨɢɯ ɞɟɣɫɬɜɢɣ (ɛɟɡɞɟɣɫɬɜɢɹ),
ɥɢɰɨ ɩɪɟɞɜɢɞɟɥɨ ɜɨɡɦɨɠɧɨɫɬɶ ɧɚɫɬɭɩɥɟɧɢɹ ɨɛɳɟɫɬɜɟɧɧɨ ɨɩɚɫɧɵɯ ɩɨɫɥɟɞɫɬɜɢɣ ɫɜɨɢɯ ɞɟɣɫɬɜɢɣ,
ɥɢɰɨ ɩɪɟɞɜɢɞɟɥɨ ɧɟɢɡɛɟɠɧɨɫɬɶ ɧɚɫɬɭɩɥɟɧɢɹ ɨɛɳɟɫɬɜɟɧɧɨ ɨɩɚɫɧɵɯ ɩɨɫɥɟɞɫɬɜɢɣ ɫɜɨɢɯ ɞɟɣɫɬɜɢɣ,
ɥɢɰɨ ɠɟɥɚɥɨ ɢɯ ɧɚɫɬɭɩɥɟɧɢɹ.
ɇɚɱɚɥɨ ɧɚɭɤɢ ɨ ɡɚɤɨɧɚɯ ɢ ɮɨɪɦɚɯ ɦɵɲɥɟɧɢɹ – ɥɨɝɢɤɢ ɫɜɹɡɵɜɚɸɬ ɫ ɢɦɟɧɟɦ Ⱥɪɢɫɬɨɬɟɥɹ (IV ɜ. ɞɨ ɧ.ɷ.). ȼ XVII ɜ. Ƚ. Ʌɟɣɛɧɢɰ (ɸɪɢɫɬ, ɧɚɩɨɦɧɢɦ) ɜɜɟɥ ɜ ɥɨɝɢɤɭ ɦɚɬɟɦɚɬɢɱɟɫɤɭɸ ɫɢɦɜɨɥɢɤɭ ɢ ɢɫɩɨɥɶɡɨɜɚɥ ɟɟ ɞɥɹ ɨɛɳɢɯ ɥɨɝɢɱɟɫɤɢɯ ɩɨɫɬɪɨɟɧɢɣ, ɬɨ ɟɫɬɶ ɩɨɥɨɠɢɥ ɧɚɱɚɥɨ ɮɨɪɦɚɥɢɡɚɰɢɢ ɥɨɝɢɤɢ. ȼ XIX ɜ. Ⱦɠ. Ȼɭɥɶ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨ ɪɟɚɥɢɡɨɜɚɥ ɢɞɟɢ Ƚ. Ʌɟɣɛɧɢɰɚ, ɩɟɪɜɵɦ ɢɫɫɥɟɞɨɜɚɥ ɚɥɝɟɛɪɚɢɱɟɫɤɢɟ ɫɜɨɣɫɬɜɚ ɜɵɫɤɚɡɵɜɚɧɢɣ, ɬɟɦ ɫɚɦɵɦ ɡɚɥɨɠɢɥ ɨɫɧɨɜɵ ɦɚɬɟɦɚɬɢɱɟɫɤɨɣ ɥɨɝɢɤɢ. ɉɨɷɬɨɦɭ ɦɚɬɟɦɚɬɢɱɟɫɤɭɸ ɥɨɝɢɤɭ ɧɟɪɟɞɤɨ ɧɚɡɵɜɚɸɬ ɛɭɥɟɜɨɣ ɚɥɝɟɛɪɨɣ ɢɥɢ ɚɥɝɟɛɪɨɣ ɥɨɝɢɤɢ.
ɉɪɨɫɬɵɟ ɜɵɫɤɚɡɵɜɚɧɢɹ ɜ ɛɭɥɟɜɨɣ ɚɥɝɟɛɪɟ ɨɛɨɡɧɚɱɚɸɬ ɛɭɤɜɚɦɢ ɢ ɧɚɡɵɜɚɸɬ ɥɨɝɢɱɟɫɤɢɦɢ ɩɟɪɟɦɟɧɧɵɦɢ. Ʌɨɝɢɱɟɫɤɚɹ ɩɟɪɟɦɟɧɧɚɹ ɦɨɠɟɬ ɩɪɢɧɢɦɚɬɶ ɨɞɧɨ ɢɡ ɞɜɭɯ ɡɧɚɱɟɧɢɣ: ɢɥɢ ɢɫɬɢɧɚ, ɢɥɢ ɥɨɠɶ. ɍɞɨɛɧɨ ɡɧɚɱɟɧɢɟ ɢɫɬɢɧɚ ɨɛɨɡɧɚɱɢɬɶ ɫɢɦɜɨɥɨɦ 1, ɚ ɡɧɚɱɟɧɢɟ ɥɨɠɶ – ɫɢɦɜɨɥɨɦ 0.
ȼ ɦɚɬɟɦɚɬɢɱɟɫɤɨɣ ɥɨɝɢɤɟ ɧɚɞ ɥɨɝɢɱɟɫɤɢɦɢ ɩɟɪɟɦɟɧɧɵɦɢ ɜɵɩɨɥɧɹɸɬ ɥɨɝɢɱɟɫɤɢɟ ɨɩɟɪɚɰɢɢ. Ʉɚɠɞɚɹ ɥɨɝɢɱɟɫɤɚɹ ɨɩɟɪɚɰɢɹ ɡɚɞɚɟɬɫɹ ɫɜɨɟɣ ɬɚɛɥɢɰɟɣ. ȼɯɨɞɨɦ ɬɚɛɥɢɰɵ ɹɜɥɹɟɬɫɹ ɩɨɥɧɵɣ ɧɚɛɨɪ ɡɧɚɱɟɧɢɣ ɜɫɟɯ ɥɨɝɢɱɟɫɤɢɯ ɩɟɪɟɦɟɧɧɵɯ – ɨɩɟɪɚɧɞɨɜ (ɚɪɝɭɦɟɧɬɨɜ) ɞɚɧɧɨɣ ɥɨɝɢɱɟɫɤɨɣ ɨɩɟɪɚɰɢɢ, ɚ ɜɵɯɨɞɨɦ – ɟɟ ɪɟɡɭɥɶɬɚɬ. Ɍɚɤɚɹ ɬɚɛɥɢɰɚ ɧɚɡɵɜɚɟɬɫɹ ɬɚɛɥɢɰɟɣ ɢɫɬɢɧɧɨɫɬɢ. Ɋɚɫɫɦɨɬɪɢɦ ɨɫɧɨɜɧɵɟ ɥɨɝɢɱɟɫɤɢɟ ɨɩɟɪɚɰɢɢ.
Ɍɚɛɥɢɰɚ 2.1
xy
0 1
10
Ɉɬɪɢɰɚɧɢɟ – ɨɞɧɨɦɟɫɬɧɚɹ ɨɩɟɪɚɰɢɹ. ȿɫɥɢ ɟɟ ɚɪ-
ɝɭɦɟɧɬɨɦ ɛɭɞɟɬ ɥɨɝɢɱɟɫɤɚɹ ɩɟɪɟɦɟɧɧɚɹ x, ɚ ɪɟɡɭɥɶɬɚɬɨɦ y, ɬɨ ɷɬɚ ɨɩɟɪɚɰɢɹ ɡɚɞɚɟɬɫɹ ɬɚɛɥ.2.1. Ʉɚɤ ɜɢɞɢɦ,
ɡɧɚɱɟɧɢɹ x ɢ y ɜɡɚɢɦɧɨ ɨɛɪɚɬɧɵ. ɉɨɷɬɨɦɭ ɞɥɹ ɨɬɪɢɰɚɧɢɹ ɢɫɩɨɥɶɡɭɸɬ ɧɚɡɜɚɧɢɟ «ɢɧɜɟɪɫɢɹ» (ɨɬ ɚɧɝɥ. Inverse – ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɫɬɶ). Ⱦɥɹ ɨɬɪɢɰɚɧɢɹ ɜɜɨɞɹɬ ɬɚɤɢɟ ɨɛɨɡɧɚɱɟɧɢɹ:
19

y ºx, ɢɥɢ y x ,
ɱɢɬɚɟɬɫɹ: y ɟɫɬɶ ɇȿ x. ɉɨɷɬɨɦɭ ɨɬɪɢɰɚɧɢɟ ɧɚɡɵɜɚɸɬ ɟɳɟ ɢ ɨɩɟɪɚɰɢɟɣ ɇȿ. ɉɭɫɬɶ x – ɭɬɜɟɪɠɞɟɧɢɟ:
|
|
|
«Ɇɚɬɟɦɚɬɢɤɚ ɸɪɢɫɬɚɦ ɧɟɨɛɯɨɞɢɦɚ». |
|
|
Ɍɨɝɞɚ ɢɧɜɟɪɫɢɟɣ ºx ɷɬɨɝɨ ɜɵɫɤɚɡɵɜɚɧɢɹ ɛɭɞɟɬ ɮɪɚɡɚ: |
|
||||
|
|
|
«ɇɟɩɪɚɜɞɚ, ɱɬɨ ɦɚɬɟɦɚɬɢɤɚ ɸɪɢɫɬɚɦ ɧɟɨɛɯɨɞɢɦɚ». |
|
|
Ɍɚɛɥɢɰɚ 2.2 |
Ʉɨɧɴɸɧɤɰɢɹ – ɦɧɨɝɨɦɟɫɬɧɚɹ ɨɩɟɪɚɰɢɹ. Ⱦɥɹ ɞɜɭɯ |
||||
|
|
|
ɥɨɝɢɱɟɫɤɢɯ ɩɟɪɟɦɟɧɧɵɯ x1 ɢ x0 ɨɧɚ ɡɚɞɚɟɬɫɹ ɬɚɛɥ.2.2. |
||
x1 |
x0 |
y |
|||
Ʉɚɤ ɜɢɞɢɦ, y 1 ɬɨɥɶɤɨ ɬɨɝɞɚ, ɤɨɝɞɚ ɂ x1 1, ɂ x0 |
1. |
||||
0 |
0 |
0 |
|||
ɉɨɷɬɨɦɭ ɤɨɧɴɸɧɤɰɢɸ ɧɚɡɵɜɚɸɬ ɟɳɟ ɨɩɟɪɚɰɢɟɣ |
ɂ. |
||||
0 |
1 |
0 |
|||
Ɉɛɨɡɧɚɱɚɸɬ ɤɨɧɴɸɧɤɰɢɸ ɫɢɦɜɨɥɨɦ (ɪɟɠɟ ɫɢɦɜɨɥɨɦ |
|||||
1 |
0 |
0 |
|||
): |
|
||||
1 |
1 |
1 |
y x1 x0 ɢɥɢ y x1 x0. |
|
|
|
|
|
|
||
Ɋɟɡɭɥɶɬɚɬ ɤɨɧɴɸɧɤɰɢɢ ɫɨɜɩɚɞɚɟɬ ɫ ɪɟɡɭɥɶɬɚɬɨɦ ɭɦɧɨɠɟɧɢɹ ɱɢɫɟɥ 1 ɢ 0. ɉɨɷɬɨɦɭ ɟɟ ɧɚɡɵɜɚɸɬ ɟɳɟ ɢ ɥɨɝɢɱɟɫɤɢɦ ɭɦɧɨɠɟɧɢɟɦ. ɉɭɫɬɶ x1 – ɭɬɜɟɪɠɞɟɧɢɟ:
«Ⱦɜɟɧɚɞɰɚɬɶ ɞɟɥɢɬɫɹ ɧɚ ɬɪɢ»,
ɚ x0 – ɜɵɫɤɚɡɵɜɚɧɢɟ:
«Ⱦɜɟɧɚɞɰɚɬɶ ɞɟɥɢɬɫɹ ɧɚ ɱɟɬɵɪɟ».
ɂɯ ɤɨɧɴɸɧɤɰɢɟɣ x1 x0 ɛɭɞɟɬ ɜɵɫɤɚɡɵɜɚɧɢɟ: «Ⱦɜɟɧɚɞɰɚɬɶ ɞɟɥɢɬɫɹ ɧɚ ɬɪɢ ɢ ɧɚ ɱɟɬɵɪɟ».
Ʉɨɧɴɸɧɤɰɢɹ n ɩɟɪɟɦɟɧɧɵɯ ɡɚɩɢɫɵɜɚɟɬɫɹ ɬɚɤ:
y xn-1 xn-2 x0.
Ɍɚɛɥɢɰɚ 2.3 |
Ⱦɢɡɴɸɧɤɰɢɹ – ɬɨɠɟ ɦɧɨɝɨɦɟɫɬɧɚɹ ɨɩɟɪɚɰɢɹ. Ⱦɥɹ |
|||
ɞɜɭɯ ɥɨɝɢɱɟɫɤɢɯ ɩɟɪɟɦɟɧɧɵɯ x1 ɢ x0 ɨɧɚ ɡɚɞɚɟɬɫɹ |
||||
x1 |
x0 |
y |
||
ɬɚɛɥ.2.3. Ʉɚɤ ɜɢɞɢɦ, y 1 ɬɨɝɞɚ, ɤɨɝɞɚ ɂɅɂ x1 1, ɂɅɂ |
||||
0 |
0 |
0 |
||
x0 1, ɂɅɂ ɨɛɚ ɚɪɝɭɦɟɧɬɚ ɪɚɜɧɵ 1 (ɤɨɝɞɚ ɯɨɬɹ ɛɵ ɨɞɢɧ |
||||
0 |
1 |
1 |
ɢɡ ɚɪɝɭɦɟɧɬɨɜ ɪɚɜɟɧ 1). ɉɨɷɬɨɦɭ ɞɢɡɴɸɧɤɰɢɸ ɧɚɡɵ- |
|
|
0 |
|
ɜɚɸɬ ɨɩɟɪɚɰɢɟɣ ɂɅɂ. Ⱦɥɹ ɨɛɨɡɧɚɱɟɧɢɹ ɞɢɡɴɸɧɤɰɢɢ |
|
1 |
1 |
|||
1 |
1 |
1 |
ɩɪɢɦɟɧɹɸɬ ɫɢɦɜɨɥ : |
|
|
||||
y x1 x0.
Ɋɟɡɭɥɶɬɚɬ ɞɢɡɴɸɧɤɰɢɢ ɜ ɬɚɛɥ.2.3, ɢɫɤɥɸɱɚɹ ɩɨɫɥɟɞɧɸɸ ɫɬɪɨɤɭ, ɫɨɜɩɚɞɚɟɬ ɫ ɪɟɡɭɥɶɬɚɬɨɦ ɫɥɨɠɟɧɢɹ ɱɢɫɟɥ 0 ɢ 1. ɉɨɷɬɨɦɭ ɟɟ ɧɚɡɵɜɚɸɬ ɟɳɟ ɥɨɝɢɱɟɫɤɢɦ ɫɥɨɠɟɧɢɟɦ. ɇɚɩɪɢɦɟɪ, x1 – ɧɟɞɨɛɪɨɫɨɜɟɫɬɧɵɣ ɤɨɧɤɭɪɟɧɬ ɩɪɢɱɢɧɢɥ ɭɛɵɬɤɢ ɞɪɭɝɨɦɭ ɯɨɡɹɣɫɬɜɭɸɳɟɦɭ ɫɭɛɴɟɤɬɭ, x0 – ɨɧ
20
