
Математика для юристов - Д.А. Ловцова
.pdf
(ɩɪɨɢɡɜɨɞɧɚɹ ɫɥɨɠɧɨɣ ɮɭɧɤɰɢɢ f(s) ɟɫɬɶ ɩɪɨɢɡɜɟɞɟɧɢɟ ɩɪɨɢɡɜɨɞɧɨɣ ɜɧɟɲɧɟɣ ɮɭɧɤɰɢɢ f ɩɨ ɚɪɝɭɦɟɧɬɭ s ɧɚ ɩɪɨɢɡɜɨɞɧɭɸ ɜɥɨɠɟɧɧɨɣ ɮɭɧɤɰɢɢ s ɩɨ ɚɪɝɭɦɟɧɬɭ x).
5. ɉɪɨɢɡɜɨɞɧɚɹ ɨɬ ɨɛɪɚɬɧɨɣ ɮɭɧɤɰɢɢ:
g’(x) |
1 |
. |
c |
||
|
f (g(x)) |
|
Ɂɞɟɫɶ ɩɪɟɞɩɨɥɚɝɚɟɬɫɹ, ɱɬɨ f(x) – ɩɪɹɦɚɹ ɮɭɧɤɰɢɹ, ɚ g(x) – ɨɛɪɚɬɧɚɹ, ɢ ɩɪɨɢɡɜɨɞɧɚɹ ɨɬ ɩɪɹɦɨɣ ɮɭɧɤɰɢɢ f’(x) ɫɭɳɟɫɬɜɭɟɬ.
ȼɫɟ ɫɜɨɣɫɬɜɚ ɞɨɤɚɡɵɜɚɸɬɫɹ ɫ ɢɫɩɨɥɶɡɨɜɚɧɢɟɦ ɨɩɪɟɞɟɥɟɧɢɹ ɩɪɨɢɡɜɨɞɧɨɣ (5.1) ɢɭɠɟɞɨɤɚɡɚɧɧɵɯɪɚɧɟɟɫɜɨɣɫɬɜ. Ⱦɨɤɚɠɟɦ, ɤɩɪɢɦɟɪɭ, ɫɜɨɣɫɬɜɨ 5, ɩɨɥɚɝɚɹ, ɱɬɨ ɜɫɟ ɩɪɟɞɵɞɭɳɢɟ ɫɜɨɣɫɬɜɚ ɭɠɟ ɞɨɤɚɡɚɧɵ. ɉɭɫɬɶ ɩɪɹɦɚɹ ɮɭɧɤɰɢɹ ɟɫɬɶ f(x), ɚ ɨɛɪɚɬɧɚɹ ɟɣ – ɮɭɧɤɰɢɹ g(x). ȿɫɥɢ ɨɧɢ ɩɪɟɞɫɬɚɜɥɟɧɵ ɜ ɨɞɧɨɣɫɢɫɬɟɦɟɤɨɨɪɞɢɧɚɬ, ɬɨɢɦɟɟɬɦɟɫɬɨɬɚɤɨɟɪɚɜɟɧɫɬɜɨ:
f(g(x)) |
x |
(5.2) |
(ɧɚɩɪɢɦɟɪ, f(x) |
x2, ɚ g(x) |
x , ɢ f(g(x)) ( x )2 x). |
ȼɨɡɶɦɟɦ ɩɪɨɢɡɜɨɞɧɵɟ ɨɬ ɥɟɜɨɣ ɢ ɩɪɚɜɨɣ ɱɚɫɬɟɣ ɪɚɜɟɧɫɬɜɚ (5.2). ɉɪɢ ɷɬɨɦ ɥɟɜɭɸ ɱɚɫɬɶ ɞɢɮɮɟɪɟɧɰɢɪɭɟɦ ɫ ɢɫɩɨɥɶɡɨɜɚɧɢɟɦ
ɩɪɚɜɢɥɚ 4: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§ |
(x 'x) x · |
|
||||
f’(g(x))ug’(x) |
lim ¨ |
|
|
|
|
¸ |
1. |
|||||
|
'x |
|
||||||||||
|
|
|
|
|
|
'xo0© |
|
¹ |
|
|||
Ɉɬɫɸɞɚ |
1 |
|
|
|
|
|
|
|
|
|
||
g’(x) |
|
|
. |
|
|
|
|
|
|
|||
|
c |
|
|
|
|
|
|
|
|
|
||
|
|
f (g(x)) |
|
|
|
|
|
|
|
|||
ɇɚɩɪɢɦɟɪ, ɞɥɹ f(x) |
x2 ɢ g(x) |
x ɢɦɟɟɦ: |
|
|
|
|||||||
|
|
|
§ |
(x 'x)2 x |
2 · |
|
|
|
||||
f’(x) |
|
lim |
¨ |
|
|
|
|
|
¸ |
2ux, |
|
|
|
¨ |
|
|
'x |
|
¸ |
|
|||||
|
'xo0© |
|
|
|
¹ |
|
|
|
||||
ɡɧɚɱɢɬ, |
|
|
1 |
|
|
|
|
|
|
|
|
|
( x )’ |
|
. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
2u( |
x) |
|
|
|
|
|
|
|||
ȼ ɬɚɛɥ. 5.1 ɫɜɟɞɟɧɵ ɩɪɨɢɡɜɨɞɧɵɟ ɨɬ ɧɟɤɨɬɨɪɵɯ ɢɡ ɷɥɟɦɟɧɬɚɪɧɵɯ ɮɭɧɤɰɢɣ. ɗɬɭ ɬɚɛɥɢɰɭ ɢ ɩɟɪɟɱɢɫɥɟɧɧɵɟ ɜɵɲɟ ɫɜɨɣɫɬɜɚ 1..5 ɢɫɩɨɥɶɡɭɸɬ ɩɪɢ ɜɵɱɢɫɥɟɧɢɢ ɩɪɨɢɡɜɨɞɧɵɯ ɥɸɛɵɯ ɮɭɧɤɰɢɣ. Ⱦɨɤɚɠɟɦ, ɧɚɩɪɢɦɟɪ, ɮɨɪɦɭɥɵ d), e), f) ɜ ɬɚɛɥ. 5.1, ɩɨɥɚɝɚɹ, ɱɬɨ ɨɫɬɚɥɶɧɵɟ ɮɨɪɦɭɥɵ ɞɨɤɚɡɚɧɵ:
61

loga (x) ln(x) , ln(a)
d) (loga(x))’ ɫɜɨɣɫɬɜɨ1ɩɪɨɢɡɜɨɞɧɵɯ ɫɬɪɨɤɚ ɫ) ɬɚɛɥ.5.1,
ex ɮɭɧɤɰɢɹ, ɨɛɪɚɬɧɚɹɤ ln(x), e) (ex)’ ɫɜɨɣɫɬɜɨ 5 ɩɪɨɢɡɜɨɞɧɵɯ,
ɫɬɪɨɤɚ ɫ) ɬɚɛɥ.5.1
ax ɮɭɧɤɰɢɹ, ɨɛɪɚɬɧɚɹ ɤ loga (x), f) (ax)’ ɫɜɨɣɫɬɜɨ 5 ɩɪɨɢɡɜɨɞɧɵɯ,
ɫɬɪɨɤɚ d) ɬɚɛɥ.5.1
ɉɪɢɦɟɪ:
1 u 1 . ln(a) x
|
1 |
|
ex. |
|
§ |
1 |
· |
||
|
||||
¨ |
|
¸ |
|
|
|
©ex ¹
ln(a)uax.
-x |
)’ |
e x ɫɥɨɠɧɚɹɮɭɧɤɰɢɹ: f(s) es |
, s(x) |
x, |
-x |
. |
(e |
ɫɜɨɣɫɬɜɨ 4 ɩɪɨɢɡɜɨɞɧɵɯ, ɫɬɪɨɤɚ e) ɬɚɛɥ.5.1 |
e |
||||
|
|
|
|
|||
5.2. Свойства дифференцируемых функций
ɉɪɨɢɡɜɨɞɧɚɹ – ɦɨɳɧɵɣ ɢɧɫɬɪɭɦɟɧɬ ɞɥɹ ɢɫɫɥɟɞɨɜɚɧɢɹ ɮɭɧɤɰɢɣ. ɉɨ ɪɟɡɭɥɶɬɚɬɚɦ ɢɫɫɥɟɞɨɜɚɧɢɣ ɭɫɬɚɧɚɜɥɢɜɚɸɬɫɹ ɫɥɟɞɭɸɳɢɟ ɫɜɨɣɫɬɜɚ ɞɢɮɮɟɪɟɧɰɢɪɭɟɦɵɯ ɮɭɧɤɰɢɣ.
ɇɟɩɪɟɪɵɜɧɨɫɬɶ. ȿɫɥɢ ɮɭɧɤɰɢɹ f(x) ɢɦɟɟɬ ɩɪɨɢɡɜɨɞɧɭɸ ɜ ɬɨɱɤɟ x a, ɬɨ ɨɧɚ ɧɟɩɪɟɪɵɜɧɚ ɜ ɷɬɨɣ ɬɨɱɤɟ. ȿɫɥɢ ɮɭɧɤɰɢɹ ɢɦɟɟɬ ɩɪɨɢɡɜɨɞɧɭɸ ɧɚ ɨɬɪɟɡɤɟ [a,b], ɬɨ ɨɧɚ ɧɟɩɪɟɪɵɜɧɚ ɧɚ ɷɬɨɦ ɨɬɪɟɡɤɟ.
ɂɫɤɥɸɱɢɜ ɢɡ ɪɚɫɫɦɨɬɪɟɧɢɹ ɜɫɟ ɡɧɚɱɟɧɢɹ x, ɜ ɤɨɬɨɪɵɯ ɮɭɧɤɰɢɹ f(x) ɢ/ɢɥɢ ɟɟ ɩɪɨɢɡɜɨɞɧɚɹ f’(x) ɧɟ ɫɭɳɟɫɬɜɭɸɬ, ɛɭɞɟɦ ɢɦɟɬɶ ɞɟɥɨ ɬɨɥɶɤɨ ɫ ɧɟɩɪɟɪɵɜɧɵɦɢ ɮɭɧɤɰɢɹɦɢ.
Ɇɨɧɨɬɨɧɧɨɫɬɶ. ȿɫɥɢ f’(x)!0 ɧɚ ɢɧɬɟɪɜɚɥɟ ]a,b[, ɬɨ ɮɭɧɤɰɢɹ ɦɨɧɨɬɨɧɧɨ ɜɨɡɪɚɫɬɚɟɬ ɧɚ ɷɬɨɦ ɢɧɬɟɪɜɚɥɟ. ȿɫɥɢ f’(x) 0 ɧɚ ɢɧɬɟɪɜɚɥɟ ]d,e[, ɬɨ ɮɭɧɤɰɢɹ ɦɨɧɨɬɨɧɧɨ ɭɛɵɜɚɟɬ ɧɚ ɷɬɨɦ ɢɧɬɟɪɜɚɥɟ. ɇɚɩɨɦɧɢɦ, ɱɬɨ ɡɧɚɱɢɬ: ɮɭɧɤɰɢɹ ɜɨɡɪɚɫɬɚɟɬ (ɢɥɢ ɭɛɵɜɚɟɬ). ɗɬɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɞɥɹ ɥɸɛɨɣ ɩɚɪɵ x2!x1 ɢɦɟɟɬ ɦɟɫɬɨ f(x2)!f(x1) (ɢɥɢ f(x2) f(x1)).
Ʉɚɤ ɦɵ ɭɠɟ ɡɧɚɟɦ, f’(x) – ɬɚɧɝɟɧɫ ɭɝɥɚ ɧɚɤɥɨɧɚ ɤɚɫɚɬɟɥɶɧɨɣ ɤ f(x) ɜ ɬɨɱɤɟ x. Ɂɧɚɱɢɬ, ɭɝɨɥ ɧɚɤɥɨɧɚ ɤɚɫɚɬɟɥɶɧɨɣ ɜ ɥɸɛɨɣ ɬɨɱɤɟ ɢɧɬɟɪɜɚɥɚ
ɜɨɡɪɚɫɬɚɧɢɹ ɮɭɧɤɰɢɢ 0 D S (ɭɱɚɫɬɨɤ AB ɤɪɢɜɨɣ f(x) ɧɚ ɪɢɫ.5.2), ɢ 2
62
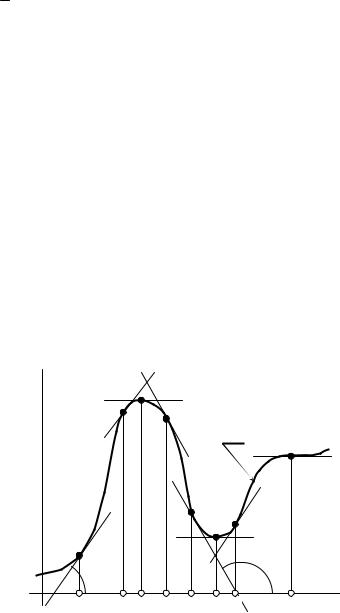
S E S ɜ ɥɸɛɨɣ ɬɨɱɤɟ ɢɧɬɟɪɜɚɥɚ ɭɛɵɜɚɧɢɹ ɮɭɧɤɰɢɢ (ɭɱɚɫɬɨɤ DE ɤɪɢ- 2
ɜɨɣ f(x) ɧɚ ɪɢɫ.5.2).
Ɇɚɤɫɢɦɭɦɵ ɢ ɦɢɧɢɦɭɦɵ. Ɍɨɱɤɚ x c ɧɚɡɵɜɚɟɬɫɹ ɬɨɱɤɨɣ ɥɨɤɚɥɶɧɨɝɨ ɦɚɤɫɢɦɭɦɚ ɮɭɧɤɰɢɢ f(x), ɟɫɥɢ ɜ ɧɟɤɨɬɨɪɨɣ ɨɤɪɟɫɬɧɨɫɬɢ ɬɨɱɤɢ c ɮɭɧɤɰɢɹ f(x) ɨɩɪɟɞɟɥɟɧɚ ɢ f(x)df(c) (ɬɨɱɤɚ C ɧɚ ɤɪɢɜɨɣ f(x) ɧɚ ɪɢɫ.5.2). Ⱥ ɬɨɱɤɚ x g ɧɚɡɵɜɚɟɬɫɹ ɬɨɱɤɨɣ ɥɨɤɚɥɶɧɨɝɨ ɦɢɧɢɦɭɦɚ ɮɭɧɤɰɢɢ f(x), ɟɫɥɢ ɜ ɧɟɤɨɬɨɪɨɣ ɨɤɪɟɫɬɧɨɫɬɢ ɬɨɱɤɢ g ɮɭɧɤɰɢɹ f(x) ɨɩɪɟɞɟɥɟɧɚ ɢ f(x)tf(g) (ɬɨɱɤɚ G ɧɚ ɤɪɢɜɨɣ f(x) ɧɚ ɪɢɫ.5.2). Ɍɨɱɤɢ ɦɚɤɫɢɦɭɦɚ ɢ ɦɢɧɢɦɭɦɚ ɮɭɧɤɰɢɢ ɧɚɡɵɜɚɸɬɫɹ ɬɨɱɤɚɦɢ ɟɟ ɷɤɫɬɪɟɦɭɦɨɜ. ȼ ɬɨɱɤɟ ɷɤɫɬɪɟɦɭɦɚ (ɪɢɫ.5.2) ɤɚɫɚɬɟɥɶɧɚɹ ɤ f(x) ɝɨɪɢɡɨɧɬɚɥɶɧɚ.
ȿɫɥɢ ɮɭɧɤɰɢɹ f(x) ɜ ɬɨɱɤɟ x xm ɞɨɫɬɢɝɚɟɬ ɥɨɤɚɥɶɧɨɝɨ ɷɤɫɬɪɟɦɭɦɚ, ɬɨ ɟɟ ɩɪɨɢɡɜɨɞɧɚɹ ɜ ɷɬɨɣ ɬɨɱɤɟ ɪɚɜɧɚ ɧɭɥɸ: f’(xm) 0.
ɗɬɨ ɭɬɜɟɪɠɞɟɧɢɟ – ɫɭɬɶ ɬ ɟ ɨ ɪ ɟ ɦ ɚ Ɏ ɟ ɪ ɦ ɚ . Ɍɨɬ ɮɚɤɬ, ɱɬɨ f’(xm) 0 – ɧɟɨɛɯɨɞɢɦɨɟ, ɧɨ ɧɟ ɞɨɫɬɚɬɨɱɧɨɟ ɭɫɥɨɜɢɟ ɷɤɫɬɪɟɦɭɦɚ ɮɭɧɤɰɢɢ ɜ ɬɨɱɤɟ x xm, ɬɨ ɟɫɬɶ ɨɛɪɚɬɧɨɟ ɭɬɜɟɪɠɞɟɧɢɟ ɨ ɬɨɦ, ɱɬɨ ɟɫɥɢ ɜ ɬɨɱɤɟ x xj ɩɪɨɢɡɜɨɞɧɚɹ f’(xj) 0, ɬɨ ɬɨɱɤɚ xj ɟɫɬɶ ɬɨɱɤɚ ɷɤɫɬɪɟɦɭɦɚ ɮɭɧɤɰɢɢ f(x), ɜɟɪɧɨ ɧɟ ɜɫɟɝɞɚ. ɇɚɩɪɢɦɟɪ, ɧɚ ɪɢɫ.5.2 ɜ ɬɨɱɤɟ J ɩɪɨɢɡɜɨɞɧɚɹ ɨɬ f(j) ɪɚɜɧɚ ɧɭɥɸ (ɤɚɫɚɬɟɥɶɧɚɹ ɤ f(x) ɜ ɷɬɨɣ ɬɨɱɤɟ ɥɟɠɢɬ ɝɨɪɢ-
ɡɨɧɬɚɥɶɧɨ), ɧɨ ɬɨɱɤɚ x |
j ɧɟ ɹɜɥɹɟɬɫɹ ɬɨɱɤɨɣ ɷɤɫɬɪɟɦɭɦɚ (ɫɥɟɜɚ ɨɬ ɧɟɟ |
|||
f(x) f(j), ɚ ɫɩɪɚɜɚ – f(x)!f(j)). |
|
|
||
y |
|
|
|
|
|
C |
|
|
|
|
B |
D |
|
|
|
|
|
f(x) |
J |
|
|
|
|
|
|
|
E |
|
|
|
|
G |
|
H |
A |
|
|
|
|
|
D |
|
|
E |
|
|
|
|
x |
a |
b |
c d e g |
h |
j |
Ɋɢɫ.5.2
63
ɋɮɨɪɦɭɥɢɪɭɟɦ ɞɨɫɬɚɬɨɱɧɵɟ ɭɫɥɨɜɢɹ ɞɥɹ ɫɭɳɟɫɬɜɨɜɚɧɢɹ ɷɤɫɬɪɟɦɭɦɚ ɮɭɧɤɰɢɢ.
ȿɫɥɢ ɮɭɧɤɰɢɹ f(x) ɧɟɩɪɟɪɵɜɧɚ ɜ ɨɤɪɟɫɬɧɨɫɬɢ ɬɨɱɤɢ xm ɢ ɢɦɟɟɬ ɩɪɨɢɡɜɨɞɧɭɸ f’(x)t0 ɫɥɟɜɚ ɨɬ xm ɢ f’(x)d0 ɫɩɪɚɜɚ ɨɬ xm, ɬɨ xm ɟɫɬɶ ɬɨɱɤɚ ɦɚɤɫɢɦɭɦɚ (ɟɫɥɢ ɡɧɚɤɢ ɜ ɧɟɪɚɜɟɧɫɬɜɚɯ ɱɟɪɟɞɭɸɬɫɹ ɜ ɨɛɪɚɬɧɨɦ ɩɨɪɹɞɤɟ, ɬɨ xm ɟɫɬɶ ɬɨɱɤɚ ɦɢɧɢɦɭɦɚ). Ⱦɪɭɝɢɦɢ ɫɥɨɜɚɦɢ, ɩɪɢ ɩɟɪɟɯɨɞɟ x ɱɟɪɟɡ ɬɨɱɤɭ xm (ɬɨɱɤɭ ɧɭɥɹ ɩɪɨɢɡɜɨɞɧɨɣ) ɩɪɨɢɡɜɨɞɧɚɹ f’(x) ɦɟɧɹɟɬ ɡɧɚɤ:
ɜ ɦɚɤɫɢɦɭɦɟ ɫ ( ) ɧɚ ( ), |
ɜ ɦɢɧɢɦɭɦɟ ɫ ( ) ɧɚ ( ). |
ɂɬɚɤ, ɩɪɨɰɟɞɭɪɚ ɨɬɵɫɤɚɧɢɹ ɷɤɫɬɪɟɦɭɦɨɜ ɮɭɧɤɰɢɢ f(x) ɫɨɫɬɨɢɬ ɜ ɫɥɟɞɭɸɳɟɦ:
ɜɵɱɢɫɥɹɸɬ ɩɪɨɢɡɜɨɞɧɭɸ f‘(x) ɡɚɞɚɧɧɨɣ ɮɭɧɤɰɢɢ f(x),
ɧɚɯɨɞɹɬ ɜɫɟ ɤɨɪɧɢ x1, x2, , xm, , xn ɭɪɚɜɧɟɧɢɹ f’(x) 0,
ɞɥɹ ɤɚɠɞɨɝɨ ɢɡ ɤɨɪɧɟɣ xm ɜɵɩɨɥɧɹɸɬ ɬɚɤɢɟ ɞɟɣɫɬɜɢɹ:
3ɨɬɫɬɭɩɚɸɬ ɨɬ xm ɜɥɟɜɨ, ɩɨɥɨɠɢɜ x xl, ɢ ɞɥɹ ɷɬɨɝɨ ɡɧɚɱɟɧɢɹ x ɨɩɪɟɞɟɥɹɸɬ ɡɧɚɤ ɩɪɨɢɡɜɨɞɧɨɣ f’(xl),
3ɨɬɫɬɭɩɚɸɬ ɨɬ xm ɜɩɪɚɜɨ, ɩɨɥɨɠɢɜ x xr, ɢ ɞɥɹ ɷɬɨɝɨ ɡɧɚɱɟɧɢɹ x ɨɩɪɟɞɟɥɹɸɬ ɡɧɚɤ ɩɪɨɢɡɜɨɞɧɨɣ f’(xr),
3ɫɪɚɜɧɢɜɚɹ ɡɧɚɤɢ ɜɟɥɢɱɢɧ f’(xl) ɢ f’(xr), ɨɩɪɟɞɟɥɹɸɬ, ɤɚɤɨɣ ɢɦɟɧɧɨ ɷɤɫɬɪɟɦɭɦ ɮɭɧɤɰɢɢ f(x) ɨɬɜɟɱɚɟɬ ɬɨɱɤɟ xm.
Ɂɧɚɱɟɧɢɹ xl ɢ xr ɜɵɛɢɪɚɸɬ ɭɞɨɛɧɵɦɢ ɞɥɹ ɜɵɱɢɫɥɟɧɢɹ ɡɧɚɱɟɧɢɣ f’(xl) ɢ f’(xr).
ɉɪɢɦɟɪ. ɂɫɫɥɟɞɭɟɦ ɮɭɧɤɰɢɸ f(x) 2ux3 6ux2 18ux 15:
ɜɵɱɢɫɥɹɟɦ f’(x) 6ux2 12ux 18.
ɪɟɲɢɜ ɭɪɚɜɧɟɧɢɟ 6ux2 12ux 18 0, ɧɚɣɞɟɦ x1 1, x2 3.
ɞɥɹ x1 ɩɨɥɨɠɢɦ xl 2, xr 0 ɢ ɧɚɯɨɞɢɦ, ɱɬɨ f’( 2) 30!0, ɚ f’(0) 18 0. Ɂɧɚɱɢɬ, ɜ ɬɨɱɤɟ x1 1 ɢɦɟɟɦ ɦɚɤɫɢɦɭɦ ɞɥɹ f(x).
ɞɥɹ x2 ɩɨɥɨɠɢɦ xl 0, xr 4 ɢ ɧɚɯɨɞɢɦ, ɱɬɨ f’(0) 18 0, ɚ
f’(4) 30!0. Ɂɧɚɱɢɬ, ɜ ɬɨɱɤɟ x2 3 ɞɥɹ f(x) ɢɦɟɟɦ ɦɢɧɢɦɭɦ. Ɂɚɞɚɧɧɚɹ ɮɭɧɤɰɢɹ ɨɩɪɟɞɟɥɟɧɚ ɧɚ ɜɫɟɣ ɱɢɫɥɨɜɨɣ ɨɫɢ. ɍɤɚɠɟɦ ɧɚ
ɭɱɚɫɬɤɢ ɟɟ ɦɨɧɨɬɨɧɧɨɫɬɢ: ɩɪɢ x x1 ɮɭɧɤɰɢɹ ɜɨɡɪɚɫɬɚɟɬ, ɧɚ ɢɧɬɟɪɜɚɥɟ ] 1, 3[ – ɭɛɵɜɚɟɬ, ɚ ɩɪɢ x!3 ɫɧɨɜɚ ɜɨɡɪɚɫɬɚɟɬ.
Ɋɚɫɫɦɨɬɪɢɦ ɬɚɤɭɸ ɮɭɧɤɰɢɸ: f(x) (x 1)3. ȿɟ ɩɪɨɢɡɜɨɞɧɚɹ f’(x) 3u(x 1)2 ɪɚɜɧɚ ɧɭɥɸ ɜ ɬɨɱɤɟ x1 1. Ɉɞɧɚɤɨ ɢ ɫɥɟɜɚ ɨɬ ɷɬɨɣ ɬɨɱɤɢ x x1, ɢ ɫɩɪɚɜɚ ɨɬ ɧɟɟ x!x1 ɩɪɨɢɡɜɨɞɧɚɹ f’(x)!0 (ɧɟ ɦɟɧɹɟɬ ɡɧɚɤɚ ɩɪɢ ɩɟɪɟɯɨɞɟ ɱɟɪɟɡ ɬɨɱɤɭ x1). Ɂɧɚɱɢɬ, ɜɷɬɨɣ ɬɨɱɤɟɷɤɫɬɪɟɦɭɦɚ ɧɟɬ.
5.3. Дифференциал функции
Ⱦɢɮɮɟɪɟɧɰɢɚɥɵ ɩɟɪɟɦɟɧɧɵɯ x, y ɢ ɞɪ. ɨɛɨɡɧɚɱɚɸɬ ɤɚɤ dx, dy ɢ ɬ.ɞ. Ɉɩɪɟɞɟɥɹɸɬɫɹ ɞɢɮɮɟɪɟɧɰɢɚɥɵ ɩɨ-ɪɚɡɧɨɦɭ, ɜ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɬɨɝɨ, ɹɜɥɹɟɬɫɹ ɥɢ ɜɟɥɢɱɢɧɚ ɧɟɡɚɜɢɫɢɦɨɣ ɩɟɪɟɦɟɧɧɨɣ ɢɥɢ ɮɭɧɤɰɢɟɣ.
64
Ⱦɢɮɮɟɪɟɧɰɢɚɥ ɧɟɡɚɜɢɫɢɦɨɣ ɩɟɪɟɦɟɧɧɨɣ – ɷɬɨ ɥɸɛɨɟ ɟɟ ɩɪɢɪɚɳɟɧɢɟ:
dx 'x.
Ⱦɢɮɮɟɪɟɧɰɢɚɥ ɮɭɧɤɰɢɢ y f(x) ɟɫɬɶ ɩɪɨɢɡɜɟɞɟɧɢɟ ɟɟ ɩɪɨɢɡɜɨɞɧɨɣ f’(x) ɧɚ ɞɢɮɮɟɪɟɧɰɢɚɥ ɧɟɡɚɜɢɫɢɦɨɣ ɩɟɪɟɦɟɧɧɨɣ dx:
dy f’(x)udx. |
(5.3) |
Ⱦɥɹ ɞɢɮɮɟɪɟɧɰɢɚɥɚ ɮɭɧɤɰɢɢ ɢɫɩɨɥɶɡɭɸɬ ɟɳɟ ɢ ɬɚɤɨɟ ɨɛɨɡɧɚɱɟɧɢɟ: d(f(x)).
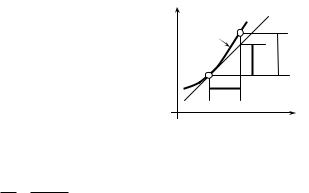
Ɋɢɫ.5.3 ɩɨɹɫɧɹɟɬ ɝɟɨɦɟɬɪɢɱɟɫɤɢɣ ɫɦɵɫɥ ɞɢɮɮɟɪɟɧɰɢɚɥɚ ɮɭɧɤɰɢɢ. Ʉɚɤ ɜɢɞɢɦ, dy – ɷɬɨ ɩɪɢɪɚɳɟɧɢɟ, ɤɨɬɨɪɨɟ ɩɨɥɭɱɚɟɬ ɨɪɞɢɧɚɬɚ ɤɚɫɚɬɟɥɶɧɨɣ ɤ f(x) ɜ ɬɨɱɤɟ x ɩɪɢ ɞɚɧɧɨɦ ɩɪɢɪɚɳɟɧɢɢ ɚɪɝɭɦɟɧɬɚ dx. Ƚɨɜɨɪɹɬ, ɱɬɨ dy ɟɫɬɶ ɝɥɚɜɧɚɹ ( ɥɢɧɟɣɧɚɹ) ɱɚɫɬɶ ɩɪɢɪɚɳɟɧɢɹ ɮɭɧɤɰɢɢ 'y. ɗɬɨ ɨɛɴɹɫɧɹɟɬɫɹ ɬɟɦ, ɱɬɨ ɩɪɢ ɦɚɥɵɯ dx ɩɪɢɪɚɳɟɧɢɟ ɮɭɧɤɰɢɢ 'y ɩɨɱɬɢ
ɫɨɜɩɚɞɚɟɬ ɫ ɟɟ ɞɢɮɮɟɪɟɧɰɢɚɥɨɦ: 'y#dy (ɪɢɫ.5.3).
y
y f(x)

 'y dy
'y dy
dx
x
Ɋɢɫ.5.3
ɂɡ ɨɩɪɟɞɟɥɟɧɢɹ ɞɢɮɮɟɪɟɧɰɢɚɥɚ ɮɭɧɤɰɢɢ (5.3) ɩɨɥɭɱɚɸɬ ɟɳɟ ɢ ɬɚɤɢɟ ɨɛɨɡɧɚɱɟɧɢɹ ɞɥɹ ɟɟ ɩɪɨɢɡɜɨɞɧɨɣ:
f’(x) dy d(f(x)) . dx dx
ɉɪɚɜɢɥɚ ɜɵɱɢɫɥɟɧɢɹ ɩɪɨɢɡɜɨɞɧɵɯ ɡɚɞɚɸɬ ɢ ɩɪɚɜɢɥɚ ɜɵɱɢɫɥɟɧɢɹ ɞɢɮɮɟɪɟɧɰɢɚɥɨɜ:
1.ȿɫɥɢ A,B const, ɬɨ d(Auf(x) Bug(x)) Audf(x) Budg(x).
2.Ⱦɢɮɮɟɪɟɧɰɢɚɥ ɩɪɨɢɡɜɟɞɟɧɢɹ ɮɭɧɤɰɢɣ:
d(f(x)ug(x)) df(x)ug(x) f(x)udg(x).
3. Ⱦɢɮɮɟɪɟɧɰɢɚɥ ɨɬɧɨɲɟɧɢɹ ɮɭɧɤɰɢɣ:
§ |
|
· |
df(x)ug(x) f(x)udg(x) . |
||
d¨ f(x) |
¸ |
||||
¨ |
|
¸ |
|
g2(x) |
|
©g(x)¹ |
|
||||
ɉɨɧɹɬɢɟ ɞɢɮɮɟɪɟɧɰɢɚɥɚ |
ɲɢɪɨɤɨ ɢɫɩɨɥɶɡɭɟɬɫɹ ɜ ɩ ɪ ɢ ɛ ɥ ɢ - |
||||
ɠ ɟ ɧ ɧ ɵ ɯ ɜ ɵ ɱ ɢ ɫ ɥ ɟ ɧ ɢ ɹ ɯ . |
Ɍɚɤ, ɞɥɹ ɨɩɪɟɞɟɥɟɧɢɹ ɩɨɝɪɟɲɧɨɫɬɢ |
||||
ɮɭɧɤɰɢɢ 'y, ɨɛɭɫɥɨɜɥɟɧɧɨɣ ɩɨɝɪɟɲɧɨɫɬɶɸ ɟɟ ɚɪɝɭɦɟɧɬɚ 'x, ɩɨɥɶɡɭɸɬɫɹ ɮɨɪɦɭɥɨɣ:
'y#dy f’(x)u'x. |
(5.4) |
65
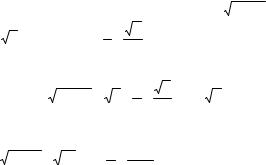
ȼɵɱɢɫɥɢɦ, ɤ ɩɪɢɦɟɪɭ, ɩɨɝɪɟɲɧɨɫɬɶ 'S ɩɥɨɳɚɞɢ ɤɪɭɝɚ S, ɟɫɥɢ ɟɝɨ ɪɚɞɢɭɫ r ɡɚɞɚɟɬɫɹ ɫ ɬɨɱɧɨɫɬɶɸ 'r. ɉɨ ɮɨɪɦɭɥɟ (5.4) ɩɨɥɭɱɢɦ:
'S (Sur2)’u'r 2uSuru'r.
Ɍɚɤ ɤɚɤ ɞɢɮɮɟɪɟɧɰɢɚɥ dy – ɨɫɧɨɜɧɚɹ ɱɚɫɬɶ ɩɪɢɪɚɳɟɧɢɹ ɮɭɧɤɰɢɢ 'y, ɩɪɢ ɦɚɥɵɯ 'x ɢɦɟɟɬ ɦɟɫɬɨ ɩɪɢɛɥɢɠɟɧɧɨɟ ɪɚɜɟɧɫɬɜɨ dy#'y ɢɥɢ ɠɟ
f(x 'x) f(x)#f’(x)u'x.
Ɉɬɫɸɞɚ
f(x 'x)#f(x) f’(x)u'x. |
(5.5) |
ɉɨɥɭɱɟɧɧɚɹ ɮɨɪɦɭɥɚ ɢɫɩɨɥɶɡɭɟɬɫɹ ɞɥɹ ɩɪɢɛɥɢɠɟɧɧɨɝɨ ɜɵɱɢɫɥɟɧɢɹ ɧɨɜɨɝɨ ɡɧɚɱɟɧɢɹ ɮɭɧɤɰɢɢ f(x 'x), ɤɨɝɞɚ ɡɚɞɚɧɵ ɟɟ ɫɬɚɪɨɟ ɡɧɚɱɟɧɢɟ f(x) ɢ ɜɟɥɢɱɢɧɚ 'x. ɇɚɣɞɟɦ, ɧɚɩɪɢɦɟɪ, ɡɧɚɱɟɧɢɟ 4 16.64 . ɉɨɥɨɠɢɦ,
ɱɬɨ ɡɞɟɫɶ f(x) 4 x . Ɍɨɝɞɚ f’(x) 1 u
4
Ɂɧɚɱɢɬ, ɩɨ ɮɨɪɦɭɥɟ (5.5) ɩɨɥɭɱɢɦ:
4 x , x 'x 16.64, x 16, ɚ 'x 0.64. x
f(x 'x) 4 x 'x #4 x 1 u |
4 x u'x |
4 x u(1 |
1 |
u |
'x |
). |
|
|
|||||
4 |
x |
|
4 x |
|||
Ɍɟɩɟɪɶ ɥɟɝɤɨ (ɩɪɚɤɬɢɱɟɫɤɢ ɜ ɭɦɟ) ɜɵɱɢɫɥɢɦ
4 16.64 #4 16 u(1 1 u 0.64 ) 2u1.01 2.02.
416
5.4.Машинные алгоритмы вычисления функций
ɉɭɫɬɶ ɮɭɧɤɰɢɹ f(x) ɜ ɡɚɞɚɧɧɨɣ ɬɨɱɤɟ a ɢ ɜ ɧɟɤɨɬɨɪɨɣ ɟɟ ɨɤɪɟɫɬɧɨɫɬɢ ɢɦɟɟɬ ɜ ɫ ɟ ɫɜɨɢ ɩɪɨɢɡɜɨɞɧɵɟ (ɬɨ ɟɫɬɶ ɨɬ ɧɟɟ ɦɨɠɧɨ ɜɡɹɬɶ ɩɪɨɢɡɜɨɞɧɭɸ ɥɸɛɨɝɨ ɩɨɪɹɞɤɚ). Ɍɨɝɞɚ ɷɬɭ ɮɭɧɤɰɢɸ ɦɨɠɧɨ ɩɪɟɞɫɬɚɜɢɬɶ ɬɚɤɨɣ ɛɟɫɤɨɧɟɱɧɨɣ ɫɭɦɦɨɣ:
f(x) |
f(a) |
f'(a) |
u(x a) |
f''(a) |
u(x a)2 |
||||||||||
|
|
||||||||||||||
|
|
f(n)(a) |
1! |
|
|
|
(n 1)(a) |
2! |
|
|
|
||||
|
|
u(x a) |
n |
|
f |
u(x a) |
n 1 |
|
|||||||
|
|
n! |
|
|
(n 1)! |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
f |
f(i)(a) |
u(x a)i . |
|
|
|
|
|
|
(5.6) |
||||
|
¦ |
|
|
|
|
|
|
|
|||||||
|
i! |
|
|
|
|
|
|
|
|
|
|
|
|
||
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ɂɞɟɫɶ ɤɨɧɫɬɪɭɤɰɢɸ k! ɧɚɡɵɜɚɸɬ ɮɚɤɬɨɪɢɚɥɨɦ:
k! 1u2u3u u(k 1)uk.
66

Ʌɟɝɤɨ ɡɚɦɟɬɢɬɶ, ɱɬɨ (k 1)! k!u(k 1). ȼ ɦɚɬɟɦɚɬɢɤɟ ɫɱɢɬɚɸɬ, ɱɬɨ 0! 1, ɩɨɷɬɨɦɭ ɩɨɫɥɟɞɧɹɹ ɮɨɪɦɭɥɚ ɪɚɛɨɬɚɟɬ ɢ ɩɪɢ k 0.
ɉɪɟɞɫɬɚɜɥɟɧɢɟ f(x) ɮɨɪɦɭɥɨɣ (5.6) ɧɚɡɵɜɚɸɬ ɪɚɡɥɨɠɟɧɢɟɦ ɮɭɧɤɰɢɢ f(x) ɜ ɪɹɞ Ɍɟɣɥɨɪɚ ɜ ɨɤɪɟɫɬɧɨɫɬɢ ɬɨɱɤɢ a. Ʉɚɤ ɜɢɞɢɦ, ɪɹɞ Ɍɟɣɥɨɪɚ ɫɨɫɬɨɢɬ ɢɡ ɛɟɫɤɨɧɟɱɧɨɝɨ ɱɢɫɥɚ ɫɥɚɝɚɟɦɵɯ. ȿɫɥɢ ɠɟ ɜ ɪɚɡɥɨɠɟɧɢɢ (5.6) ɨɝɪɚɧɢɱɢɬɶɫɹ ɤɨɧɟɱɧɵɦ ɱɢɫɥɨɦ ɫɥɚɝɚɟɦɵɯ, ɬɨɝɞɚ ɷɬɨ ɬɨɱɧɨɟ ɪɚɜɟɧɫɬɜɨ ɧɭɠɧɨ ɡɚɦɟɧɢɬɶ ɩɪɢɛɥɢɠɟɧɧɵɦ:
f(x) # M(x) f(a) |
f' |
(a) |
u(x a) |
|
f''(a) |
u(x a) |
2 |
|
|
f(n)(a) |
u(x a) |
n |
|||||||||||||||||||||
1! |
|
|
2! |
|
|
|
n! |
|
|||||||||||||||||||||||||
|
|
(i) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
n |
(a) |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
¦ |
f |
|
u(x a)i |
|
|
¦ui . |
|
|
|
|
|
|
|
|
|
|
|
(5.7) |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
i 0 |
i! |
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
f(i)(a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ɂɞɟɫɶ ui |
u(x a)i |
– ɫɥɚɝɚɟɦɨɟ ɧɨɦɟɪ i ɜ ɫɭɦɦɟ (5.7). |
|
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
i! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɉɪɢɛɥɢɠɟɧɧɨɟ ɪɚɜɟɧɫɬɜɨ (5.7), ɬɨ ɟɫɬɶ ɭɫɟɱɟɧɧɵɣ ɪɹɞ (5.6), ɢ |
||||||||||||||||||||||||||||||
ɧɚɡɵɜɚɸɬ ɮɨɪɦɭɥɨɣ Ɍɟɣɥɨɪɚ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
ȼɫɟ, ɱɬɨ ɧɟ ɜɨɲɥɨ ɜ ɫɭɦɦɭ (5.7) ɢɡ ɮɨɪɦɭɥɵ (5.6), ɚ ɢɦɟɧɧɨ, |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
f |
(i) |
(a) |
|
|
|
|
|
|
f |
(n 1) |
([) |
|
|
|
||||
|
|
|
f(x) M(x) Rn+1(x) |
¦ |
|
|
u(x a)i |
|
|
|
u(x a)(n 1) , |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i n 1 |
|
i! |
|
|
|
|
|
|
(n 1)! |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ɧɚɡɵɜɚɸɬ ɨ ɫ ɬ ɚ ɬ ɨ ɱ ɧ ɵ ɦ |
|
ɱ ɥ ɟ ɧ ɨ ɦ |
ɪɹɞɚ Ɍɟɣɥɨɪɚ. Ɂɞɟɫɶ [ – ɧɟ- |
||||||||||||||||||||||||||||||
ɤɨɬɨɪɚɹ ɬɨɱɤɚ ɜɧɭɬɪɢ ɨɬɪɟɡɤɚ [a, x]. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
Ⱦɨɤɚɡɚɧɨ, ɱɬɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
lim |
|
f(n 1)([) |
|
u(x |
a) |
(n 1) |
0 . |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
(n 1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
xoa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ȿɫɥɢ ɩɪɨɢɡɜɨɞɧɚɹ f(n+1)(x) ɩɪɢ nof ɨɫɬɚɟɬɫɹ ɨɝɪɚɧɢɱɟɧɧɨɣ, ɬɨ ɢ |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
lim |
|
|
f(n 1)([) |
u(x |
a) |
(n 1) |
0 . |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
nof (n 1)!
ɉɨɷɬɨɦɭ ɩɪɢ ɨɝɪɚɧɢɱɟɧɧɨɣ ɩɪɨɢɡɜɨɞɧɨɣ f(n+1)(x) ɡɧɚɱɟɧɢɟ f(n+1)([) (ɞɥɹ ɧɟɨɩɪɟɞɟɥɟɧɧɨɝɨ [) ɧɟ ɫɢɥɶɧɨ ɨɬɥɢɱɚɟɬɫɹ ɨɬ ɜɟɥɢɱɢɧɵ f(n+1)(a) (ɡɧɚɱɟɧɢɟ a ɡɚɞɚɧɨ), ɬɨ ɟɫɬɶ
Rn+1(x)# f(n 1)(a) u(x a)(n 1) . (n 1)!
Ɂɧɚɱɢɬ,
67

~f(x) M(x)~# f(n 1)(a) u(x a)(n 1) ~un+1~, (n 1)!
ɢ ɚɛɫɨɥɸɬɧɭɸ ɩɨɝɪɟɲɧɨɫɬɶ ɩɪɟɞɫɬɚɜɥɟɧɢɹ ɮɭɧɤɰɢɢ f(x) ɜ ɨɤɪɟɫɬɧɨɫɬɢ ɬɨɱɤɢ a ɤɨɧɟɱɧɨɣ ɫɭɦɦɨɣ (5.7) ɦɨɠɧɨ ɨɰɟɧɢɬɶ ɜɟɥɢɱɢɧɨɣ ~un+1~ – ɦɨɞɭɥɟɦ ɩɟɪɜɨɝɨ ɢɡ ɨɬɛɪɨɲɟɧɧɵɯ ɫɥɚɝɚɟɦɵɯ ɜ ɪɹɞɟ Ɍɟɣɥɨɪɚ (5.6). Ɉɱɟɜɢɞɧɨ, ɱɬɨ ɫ ɭɜɟɥɢɱɟɧɢɟɦ n ɢ ɩɪɢ ɭɦɟɧɶɲɟɧɢɢ ɪɚɡɧɨɫɬɢ (x a) ɷɬɚ ɩɨɝɪɟɲɧɨɫɬɶ ɫɧɢɠɚɟɬɫɹ.
ȿɫɥɢ ɜ ɮɨɪɦɭɥɟ (5.7) ɩɨɥɨɠɢɬɶ a 0, ɩɨɥɭɱɢɦ ɱɚɫɬɧɵɣ ɫɥɭɱɚɣ ɮɨɪɦɭɥɵ Ɍɟɣɥɨɪɚ, ɤɨɬɨɪɵɣ ɧɚɡɵɜɚɟɬɫɹ ɮɨɪɦɭɥɨɣ Ɇɚɤɥɨɪɟɧɚ:
n |
(i) |
(0) |
|
|
|
M(x) ¦ |
f |
|
u xi . |
(5.8) |
|
|
|
|
|||
i 0 |
i! |
|
|||
|
|
|
|
||
Ɏɨɪɦɭɥɚ Ɇɚɤɥɨɪɟɧɚ ɨɬɥɢɱɚɟɬɫɹ ɨɬ ɮɨɪɦɭɥɵ Ɍɟɣɥɨɪɚ ɥɢɲɶ ɧɚɱɚɥɨɦ ɨɬɫɱɟɬɚ ɩɟɪɟɦɟɧɧɨɣ x. ȿɫɥɢ ɜ ɮɨɪɦɭɥɟ (5.7) ɧɚɱɚɥɨ ɨɬɫɱɟɬɚ ɜɟɥɢɱɢɧɵ x ɩɟɪɟɧɟɫɬɢ ɜ ɬɨɱɤɭ a, ɬɨ ɨɧɚ ɩɪɟɨɛɪɚɡɭɟɬɫɹ ɜ ɮɨɪɦɭɥɭ (5.8). ɉɨɷɬɨɦɭ ɧɢɠɟ ɩɪɢ ɢɫɩɨɥɶɡɨɜɚɧɢɢ ɮɨɪɦɭɥɵ (5.7) ɦɵ ɛɭɞɟɦ ɩɨɥɚɝɚɬɶ, ɱɬɨ a 0.
ɍɤɚɠɟɦ ɧɚ ɨɫɧɨɜɧɵɟɞɨɫɬɨɢɧɫɬɜɚ ɩɪɟɞɫɬɚɜɥɟɧɢɹɮɭɧɤɰɢɢ f(x) ɮɨɪɦɭɥɨɣ Ɍɟɣɥɨɪɚ:
9ɜ ɮɨɪɦɭɥɟ (5.7) ɩɪɢ ɜɵɱɢɫɥɟɧɢɢ ɡɧɚɱɟɧɢɹ M(x) ɞɥɹ f(x) ɥɸɛɨɝɨ ɜɢɞɚ (!) ɧɚɞ ɡɚɞɚɧɧɵɦ x ɩɪɨɢɡɜɨɞɹɬɫɹ ɬɨɥɶɤɨ ɚɪɢɮɦɟɬɢɱɟɫɤɢɟ ɞɟɣɫɬɜɢɹ,
9ɩɨɝɪɟɲɧɨɫɬɶ ɩɪɢɛɥɢɠɟɧɢɹ ɮɭɧɤɰɢɢ f(x) ɮɨɪɦɭɥɨɣ (5.7) ɪɟɝɭɥɢɪɭɟɦɚ. ȿɫɥɢ ɬɨɱɧɨɫɬɶ ɜɵɱɢɫɥɟɧɢɹ ɮɭɧɤɰɢɢ H ɡɚɞɚɧɚ, ɬɨ ɤɨɥɢɱɟɫɬɜɨ ɫɥɚɝɚɟɦɵɯ (n 1) ɜ ɮɨɪɦɭɥɟ (5.7) ɭɜɟɥɢɱɢɜɚɸɬ ɞɨ ɬɟɯ ɩɨɪ, ɩɨɤɚ ɧɟ ɜɵɩɨɥɧɢɬɫɹ ɭɫɥɨɜɢɟ
~un+1~ f(n 1)(0) ux(n 1) d H,
(n 1)!
9 ɨɛɵɱɧɨ ɫɨɫɟɞɧɢɟ ɫɥɚɝɚɟɦɵɟ ui ɢ ui+1 ɜ ɫɭɦɦɟ (5.7) ɫɜɹɡɚɧɵ ɩɪɨɫɬɵɦ ɫɨɨɬɧɨɲɟɧɢɟɦ. ɉɨɷɬɨɦɭ ɞɥɹ ɜɵɱɢɫɥɟɧɢɹ ɨɱɟɪɟɞɧɨɝɨ ɫɥɚɝɚɟɦɨɝɨ ui+1 ɢɫɩɨɥɶɡɭɟɬɫɹ ɩɪɟɞɵɞɭɳɟɟ, ɭɠɟ ɧɚɣɞɟɧɧɨɟ ui.
ɂɦɟɧɧɨ ɩɨɷɬɨɦɭ ɪɚɡɥɨɠɟɧɢɟ ɮɭɧɤɰɢɣ ɜ ɪɹɞ Ɍɟɣɥɨɪɚ ɫɨɫɬɚɜɥɹɟɬ ɨɫɧɨɜɭ ɩɨɫɬɪɨɟɧɢɹ ɦɚɲɢɧɧɵɯ ɚɥɝɨɪɢɬɦɨɜ ɢɯ ɜɵɱɢɫɥɟɧɢɹ.
Ɋɚɡɪɚɛɨɬɚɟɦ ɞɥɹ ɩɪɢɦɟɪɚ ɚɥɝɨɪɢɬɦ ɜɵɱɢɫɥɟɧɢɹ ɮɭɧɤɰɢɢ y f(x) cos(x).
ɋɧɚɱɚɥɚ ɪɚɡɥɨɠɢɦ ɡɚɞɚɧɧɭɸ ɮɭɧɤɰɢɸ ɜ ɪɹɞ Ɍɟɣɥɨɪɚ. ɂɦɟɟɦ f(x) cos(x). ȼɵɱɢɫɥɹɟɦ ɫɥɚɝɚɟɦɵɟ ɜ ɫɭɦɦɟ (5.7):
68
f(x) |
cos(x), |
f(0) |
1, |
u0 |
1, |
|
|
|
|
||||||
f’(x) |
sin(x), |
f’(0) |
0, |
u1 |
0, |
|
|
2 |
|
||||||
f |
(2) |
|
|
|
(2) |
|
|
|
|
|
x |
|
|||
(x) |
cos(x), |
f |
(0) |
1, |
u2 |
|
|
|
|
, |
|||||
2! |
|||||||||||||||
f(3)(x) |
sin(x), |
f(3)(0) |
0, |
u3 |
0, |
|
|||||||||
|
|
|
|
||||||||||||
f |
(4) |
|
|
|
(2) |
|
|
|
|
x4 |
|
|
|||
(x) |
cos(x), |
f |
(0) |
1, |
u2 |
|
|
. |
|
||||||
4! |
|
||||||||||||||
Ʉɚɤ ɜɢɞɢɦ, ɞɥɹ f(x) cos(x) ɜ ɪɚɡɥɨɠɟɧɢɢ (5.7) ɜɫɟ ɧɟɱɟɬɧɵɟ ɫɥɚɝɚɟɦɵɟ ɡɚɜɟɞɨɦɨ ɪɚɜɧɵ ɧɭɥɸ. Ɉɬɛɪɨɫɢɦ ɢɯ, ɚ ɨɫɬɚɜɲɢɟɫɹ ɫɥɚɝɚɟɦɵɟ ɩɪɨɧɭɦɟɪɭɟɦ ɡɚɧɨɜɨ. Ɍɚɤ ɩɨɥɭɱɢɦ ɫɥɟɞɭɸɳɭɸ ɮɨɪɦɭɥɭ ɪɚɡɥɨɠɟɧɢɹ ɮɭɧɤɰɢɢ f(x) cos(x) ɜ ɪɹɞ Ɍɟɣɥɨɪɚ M(x):
|
x2 |
|
x4 |
n |
|
x2un |
|
y cos(x)#M(x) 1 |
|
|
|
1 |
u |
|
|
2! |
4! |
n! |
|||||
|
|
|
|
n |
i |
|
x2ui |
|
¦ |
1 |
u |
|
|
2ui ! |
||||
i 0 |
|
|
||
|
|
|
n |
|
¦ui |
(5.9) |
i 0 |
|
Ⱥ ɬɟɩɟɪɶ ɪɚɡɪɚɛɚɬɵɜɚɟɦ ɩɪɨɰɟɞɭɪɭ ɜɵɱɢɫɥɟɧɢɹ ɜɟɥɢɱɢɧɵ y f(x) cos(x) ɩɨɮɨɪɦɭɥɟ (5.9) ɞɥɹɡɚɞɚɧɧɨɝɨ x ɫɬɪɟɛɭɟɦɨɣɬɨɱɧɨɫɬɶɸ H.
ɇɚɤɨɩɥɟɧɢɟ ɫɭɦɦɵ (5.9) ɨɪɝɚɧɢɡɭɟɦ ɬɚɤ: ɤ ɩɪɟɞɵɞɭɳɟɣ ɫɭɦɦɟ yi ɩɪɢɛɚɜɥɹɟɦ ɨɱɟɪɟɞɧɨɟ ɫɥɚɝɚɟɦɨɟ ui ɢ ɩɨɥɭɱɚɟɦ ɧɨɜɨɟ ɡɧɚɱɟɧɢɟ ɫɭɦɦɵ yi+1. Ɂɚɬɟɦ ɜɵɱɢɫɥɹɟɦ ɫɥɟɞɭɸɳɟɟ ɫɥɚɝɚɟɦɨɟ ui+1. ɇɨ ɩɪɟɠɞɟ ɧɚɣɞɟɦ ɫɜɹɡɶ ɦɟɠɞɭ ɫɨɫɟɞɧɢɦɢ ɫɥɚɝɚɟɦɵɦɢ ui+1 ɢ ui ɜ ɷɬɨɣ ɫɭɦɦɟ:
ui 1 |
( 1)i 1 u |
x2u(i 1) |
|
|||||||
(2u(i 1))! |
||||||||||
|
|
|
|
|
|
|||||
( 1)i u |
x2ui |
|
u( 1)u |
|
|
x2 |
||||
|
|
(2ui 1)u(2ui 2) |
||||||||
|
|
|
(2ui)! |
|||||||
ui u |
|
|
x2 |
|
. |
|
||||
|
|
|
|
|
|
|||||
|
|
2 u(i 1) u 2 ui |
||||||||
Ɂɞɟɫɶ i 0,1,2, |
|
|
, y0 |
0, u0 1. |
|
|
|
|||
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɞɥɹ ɡɚɞɚɧɧɨɝɨ x ɩɪɨɰɟɞɭɪɚ ɜɵɱɢɫɥɟɧɢɹ ɜɟɥɢɱɢɧɵ y cos(x) ɫ ɬɨɱɧɨɫɬɶɸ H ɨɩɢɫɵɜɚɟɬɫɹ ɫɥɟɞɭɸɳɢɦɢ ɫɨɨɬɧɨɲɟɧɢɹɦɢ:
yi 1 |
yi ui, |
|
|
||
° |
|
|
x2 |
(5.10) |
|
® |
|
|
|||
°ui 1 |
ui u |
|
|
, |
|
2ui 1 u 2ui 2 |
|||||
¯ |
|
|
|||
i 0,1,2,..., ɩɨɤɚ ~ui~!H,
69
y0 0, u0 1.
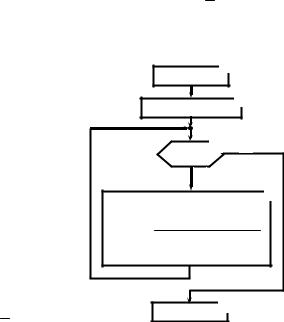
ɇɚ ɪɢɫ.5.4 ɩɨɤɚɡɚɧ ɝɪɚɮ ɚɥɝɨɪɢɬɦɚ ɪɟɲɟɧɢɹ ɩɨɫɬɚɜɥɟɧɧɨɣ ɡɚɞɚɱɢ. ȼ ɛɥɨɤɟ 0 ɡɚɞɚɸɬ ɡɧɚɱɟɧɢɟ ɚɪɝɭɦɟɧɬɚ x ɢ ɬɪɟɛɭɟɦɭɸ ɬɨɱɧɨɫɬɶ ɜɵɱɢɫɥɟɧɢɹ H. ȼ ɛɥɨɤɟ 1 ɡɚɞɚɸɬ ɧɚɱɚɥɶɧɵɟ ɭɫɥɨɜɢɹ ɞɥɹ ɮɨɪɦɭɥɵ (5.10), ɚ ɢɦɟɧɧɨ, ɢɫɯɨɞɧɨɟ ɡɧɚɱɟɧɢɟ y0 ɜ ɫɭɦɦɟ (5.9), ɩɟɪɜɨɟ ɫɥɚɝɚɟɦɨɟ u0 ɜ ɧɟɣ, ɫɱɟɬɱɢɤɚ i ɬɟɤɭɳɟɝɨ ɱɢɫɥɚ ɫɥɚɝɚɟɦɵɯ ɜ ɫɭɦɦɟ (5.9). ȼ ɛɥɨɤɟ 2 ɩɪɨɜɟɪɹɟɬɫɹ ɭɫɥɨɜɢɟ ~u~!H. ɉɨɤɚ ɨɧɨ ɜɟɪɧɨ, ɩɟɪɟɣɬɢ ɤ ɛɥɨɤɭ 3 (ɩɪɨɞɨɥɠɢɬɶ ɧɚɤɨɩɥɟɧɢɟ ɫɭɦɦɵ). Ʉɚɤ ɬɨɥɶɤɨ ɷɬɨ ɭɫɥɨɜɢɟ ɧɚɪɭɲɟɧɨ, ɩɟɪɟɣɬɢ ɤ ɛɥɨɤɭ 4. Ȼɥɨɤ 3 ɜɤɥɸɱɚɟɬ ɜ ɫɟɛɹ ɫɨɨɬɧɨɲɟɧɢɹ (5.10). Ɉɬɦɟɬɢɦ, ɱɬɨ ɜɫɟ ɩɟɪɟɦɟɧɧɵɟ ɪɟɲɚɟɦɨɣ ɡɚɞɚɱɢ – ɩɪɨɫɬɵɟ, ɩɨɷɬɨɦɭ ɢɧɞɟɤɫɵ ɭ ɧɢɯ ɭɛɪɚɧɵ, ɬɨ ɟɫɬɶ ɜɦɟɫɬɨ yi+1 yi ui ɡɚɩɢɫɵɜɚɟɦ y: y u, ɱɬɨ ɨɡɧɚɱɚɟɬ: ɧɨɜɨɟ ɡɧɚɱɟɧɢɟ y (ɫɥɟɜɚ ɨɬ ɫɢɦɜɨɥɚ: ) ɟɫɬɶ ɟɝɨ ɫɬɚɪɨɟ ɡɧɚɱɟɧɢɟ (ɫɩɪɚɜɚ ɨɬ ɫɢɦɜɨɥɚ : ) ɩɥɸɫ ɨɱɟɪɟɞɧɨɟ ɫɥɚɝɚɟɦɨɟ u. Ɂɞɟɫɶ ɠɟ ɭɜɟɥɢɱɢɜɚɟɦ i – ɩɨɤɚɡɚɧɢɹ ɫɱɟɬɱɢɤɚ ɞɥɹ ɱɢɫɥɚ ɫɥɚɝɚɟɦɵɯ ɜ ɫɭɦɦɟ ɞɥɹ y.
ȼɵɩɨɥɧɢɦ ɪɭɱɧɭɸ ɩɪɨɤɪɭɬɤɭ ɷɬɨɝɨ ɚɥɝɨɪɢɬɦɚ ɞɥɹ x S ɢ H 0.025.
Ⱦɟɣɫɬɜɭɟɦ ɩɨ ɪɢɫ. 5.4: |
|
|
|
|
|
3 |
|
|||
|
|
|
|
|
|
|
||||
0: x |
1.047; |
H |
0.025. |
|
|
|
|
0 |
||
1: y |
0; |
|
u |
1.000; |
i |
0. |
|
|
||
|
|
Ɂɚɞɚɬɶ x, H |
||||||||
|
2: 1.000!0.025? Ⱦɚ. |
i |
1. |
y: 0, u: 1, i: |
0 1 |
|||||
|
3: y |
1.000; |
u |
0.548; |
|
|
|
|||
|
2: 0.548!0.025? Ⱦɚ. |
i |
2. |
|
~u~!H 2 |
0 |
||||
|
3: y |
0.452; |
u |
0.050; |
|
1 |
|
|||
|
2: 0.050!0.025? Ⱦɚ. |
|
|
|
3 |
|||||
|
|
|
|
y: y u, |
||||||
|
3: y |
0.502; u 0.002; |
i |
3. |
|
|
||||
|
|
x2 |
|
|||||||
|
2: 0.002!0.025? ɇɟɬ. |
|
u: uu |
, |
||||||
|
|
|
|
(2ui 1)u(2ui 2) |
||||||
|
|
|
|
|
|
|
|
|
||
|
4: y |
0.502. |
|
|
|
|
|
|
i: i 1. |
|
Ʉɚɤ ɜɢɞɢɦ, ɜɫɟɝɨ ɬɪɟɯ ɫɥɚɝɚɟɦɵɯ ɜ |
|
|
|
|
|
|||||
ɫɭɦɦɟ (5.10) ɨɤɚɡɚɥɨɫɶ ɞɨɫɬɚɬɨɱɧɨ |
|
|
|
ȼɵɜɨɞ y 4 |
||||||
ɞɥɹ ɜɵɱɢɫɥɟɧɢɹ y cos( |
S |
) ɫ ɬɨɱɧɨ- |
|
|
|
|||||
3 |
|
|
|
|
|
|||||
ɫɬɶɸ H 0.025. |
|
|
|
|
|
|
Ɋɢɫ.5.4 |
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
70
