
Математика для юристов - Д.А. Ловцова
.pdfɧɨɫɬɶ ɫɨɛɵɬɢɹ «ɪɨɜɧɨ ɞɜɚ ɩɨɩɚɞɚɧɢɹ ɩɪɢ ɬɪɟɯ ɜɵɫɬɪɟɥɚɯ» ɤɚɤ P32 ɢ
ɩɪɢɦɟɧɢɦ ɞɥɹ ɟɟ ɜɵɱɢɫɥɟɧɢɹ ɮɨɪɦɭɥɵ ɫɥɨɠɟɧɢɹ ɢ ɭɦɧɨɠɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ:
P32 P(A1uA2uºA3) P(A1uºA2uA3) P(ºA1uA2uA3) pupuq puqup qupup 3up2uq.
P32 C32 up2uq.
Ɍɚɤ ɦɵ ɩɨɥɭɱɢɥɢ ɮɨɪɦɭɥɭ Ȼɟɪɧɭɥɥɢ ɞɥɹ ɫɟɪɢɢ ɢɡ n 3 ɢɫɩɵɬɚɧɢɣ, ɜ ɤɨɬɨɪɵɯ ɫɨɛɵɬɢɟ A ɧɚɫɬɭɩɢɥɨ ɪɨɜɧɨ m 2 ɪɚɡɚ.
ȼ ɨɛɳɟɦ ɫɥɭɱɚɟ ɮɨɪɦɭɥɚ Ȼɟɪɧɭɥɥɢ ɡɚɩɢɫɵɜɚɟɬɫɹ ɬɚɤ:
Pnm Cnm upmuqn-m. |
(7.19) |
Ɉɧɚ ɩɪɢɦɟɧɹɟɬɫɹ ɩɪɢ ɪɟɲɟɧɢɢ ɬɚɤɢɯ ɡɚɞɚɱ. ɉɭɫɬɶ ɜ ɪɟɡɭɥɶɬɚɬɟ ɫɥɭɱɚɣɧɨɝɨ ɢɫɩɵɬɚɧɢɹ ɧɟɤɨɬɨɪɨɟ ɫɨɛɵɬɢɟ A ɦɨɠɟɬ ɧɚɫɬɭɩɢɬɶ ɢɥɢ ɧɟ ɧɚɫɬɭɩɢɬɶ. ɇɚɫɬɭɩɥɟɧɢɟ ɷɬɨɝɨ ɫɨɛɵɬɢɹ ɜ ɞɚɧɧɨɦ ɢɫɩɵɬɚɧɢɢ ɧɚɡɵɜɚɸɬ ɭɫɩɟɯɨɦ. ɂɫɩɵɬɚɧɢɟ ɩɨɜɬɨɪɹɸɬ n ɪɚɡ. ɉɪɢ ɷɬɨɦ ɫɨɛɥɸɞɚɸɬɫɹ ɫɥɟɞɭɸɳɢɟ ɭɫɥɨɜɢɹ:
ɜɟɪɨɹɬɧɨɫɬɶ ɭɫɩɟɯɚ P(A) p ɜ ɤɚɠɞɨɦ ɢɫɩɵɬɚɧɢɢ ɨɞɧɚ
ɢ ɬɚ ɠɟ,
ɪɟɡɭɥɶɬɚɬ ɥɸɛɨɝɨ ɢɫɩɵɬɚɧɢɹ ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɪɟɡɭɥɶɬɚɬɨɜ ɩɪɟɞɵɞɭɳɢɯ ɢɫɩɵɬɚɧɢɣ.
ɋɩɪɚɲɢɜɚɟɬɫɹ, ɤɚɤɨɜɚ ɜɟɪɨɹɬɧɨɫɬɶ Pnm ɬɨɝɨ, ɱɬɨ ɜ n ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɵɯ ɧɟɡɚɜɢɫɢɦɵɯ ɢɫɩɵɬɚɧɢɹɯ ɭɫɩɟɯ ɛɭɞɟɬ ɞɨɫɬɢɝɧɭɬ ɪɨɜɧɨ m ɪɚɡ?
Ɉɬɜɟɬ ɧɚ ɷɬɨɬ ɜɨɩɪɨɫ ɢ ɞɚɟɬ ɮɨɪɦɭɥɚ Ȼɟɪɧɭɥɥɢ (7.19). ɂɡ ɷɬɨɣ ɮɨɪɦɭɥɵ ɦɨɠɧɨ ɜɵɜɟɫɬɢ ɬɚɤɢɟ ɩɪɨɫɬɵɟ ɫɥɟɞɫɬɜɢɹ:
1. Pnn pn; Pn0 qn; 2. Pn0 Pn1 Pnn 1 Pnn 1.
ɉɪɢɦɟɪ. ȼ ɭɪɧɟ 2 ɛɟɥɵɯ ɢ 2 ɱɟɪɧɵɯ ɲɚɪɚ. ɂɡ ɧɟɟ ɧɚɭɝɚɞ ɜɵɧɢɦɚɸɬ 2 ɲɚɪɚ ɢ ɜɨɡɜɪɚɳɚɸɬ ɢɯ ɨɛɪɚɬɧɨ. ɗɬɨ ɢɫɩɵɬɚɧɢɟ ɜɵɩɨɥɧɹɸɬ 4 ɪɚɡɚ. ɇɚɣɬɢ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ:
ɚ) ɲɚɪɵ ɪɚɡɧɨɝɨ ɰɜɟɬɚ ɜɵɧɭɬɵ ɪɨɜɧɨ 3 ɪɚɡɚ, ɛ) ɲɚɪɵ ɪɚɡɧɨɝɨ ɰɜɟɬɚ ɜɵɧɭɬɵ ɯɨɬɹ ɛɵ ɨɞɢɧ ɪɚɡ.
Ɋɟɲɟɧɢɟ.
ɚ) Ɉɱɟɜɢɞɧɨ, ɱɬɨ ɡɞɟɫɶ ɧɭɠɧɨ ɜɵɱɢɫɥɢɬɶ P43 ɩɨ ɮɨɪɦɭɥɟ (7.19). ɍɫɩɟɯ ɢɫɩɵɬɚɧɢɹ A ɫɨɫɬɨɢɬ ɜ ɬɨɦ, ɱɬɨ ɢɡ ɭɪɧɵ ɜɵɧɭɬɵ ɲɚɪɵ ɪɚɡɧɨɝɨ ɰɜɟɬɚ, ɢ ɞɥɹ ɩɪɢɦɟɧɟɧɢɹ ɮɨɪɦɭɥɵ (7.19) ɧɭɠɧɨ ɧɚɣɬɢ P(A) p ɢ q 1 p.
ɉɪɢ ɤɚɠɞɨɦ ɢɫɩɵɬɚɧɢɢ ɢɡ ɭɪɧɵ ɛɟɪɭɬ 2 ɲɚɪɚ ɢɡ 4. ɍ ɬɚɤɨɝɨ ɢɫ-
ɩɵɬɚɧɢɹ ɦɨɠɟɬ ɛɵɬɶ m(:) |
2 |
4 u3 |
6 |
ɢɫɯɨɞɨɜ. ɂɡ ɧɢɯ ɛɥɚɝɨɩɪɢɹɬ- |
|
C4 |
|
||||
2 u1 |
|||||
|
|
|
|
||
|
|
|
|
111 |
ɧɵɦɢ ɞɥɹ A ɛɭɞɭɬ ɢɫɯɨɞɵ ɫ ɲɚɪɚɦɢ ɪɚɡɧɨɝɨ ɰɜɟɬɚ. Ɍɚɤɢɟ ɢɫɯɨɞɵ ɨɛɪɚɡɭɸɬɫɹ ɬɚɤ. Ʉɚɠɞɵɣ ɢɡ 2 ɛɟɥɵɯ ɲɚɪɨɜ ɦɨɠɟɬ ɫɨɱɟɬɚɬɶɫɹ ɫ ɥɸɛɵɦ ɢɡ 2 ɱɟɪɧɵɯ, ɬɨ ɟɫɬɶ ɞɟɣɫɬɜɢɟ «ɜɵɧɭɬɶ ɲɚɪɵ ɪɚɡɧɨɝɨ ɰɜɟɬɚ» ɪɟɚɥɢɡɭɟɬɫɹ ɞɜɭɦɹ ɫɩɨɫɨɛɚɦɢ – ɨɞɢɧ ɛɟɥɵɣ ɫ ɥɸɛɵɦ ɢɡ ɞɜɭɯ ɱɟɪɧɵɯ. Ⱥ ɜɫɟɝɨ ɬɚɤɢɯ ɞɟɣɫɬɜɢɣ ɞɜɚ – ɞɜɚ ɛɟɥɵɯ. Ɂɧɚɱɢɬ, ɩɨ ɩɪɚɜɢɥɭ ɭɦɧɨɠɟɧɢɹ ɢɡ
ɤɨɦɛɢɧɚɬɨɪɢɤɢ (ɩ. 7.1) m(A) 2u2 |
4. Ɉɬɫɸɞɚ |
ɩɨ ɨɩɪɟɞɟɥɟɧɢɸ |
|||||||||||||||
P(A) |
4 |
|
2 |
p, ɚ q |
1 p |
1 |
. Ɍɟɩɟɪɶ |
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
||||||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
3 |
3 |
3 |
1 |
3 |
§2 |
·3 |
|
1 |
|
32 |
|
||
|
|
|
|
P4 |
C4 up uq |
C4 up uq |
4u¨ |
|
¸ |
u |
|
|
|
#0.4. |
|||
|
|
|
|
|
3 |
|
81 |
||||||||||
|
|
|
|
|
|
|
|
|
|
©3 |
¹ |
|
|
|
|||
ɛ) Ɏɪɚɡɚ «ɯɨɬɹ ɛɵ ɨɞɢɧ ɪɚɡ» ɨɡɧɚɱɚɟɬ, ɱɬɨ ɢɦɟɟɬ ɦɟɫɬɨ ɫɨɛɵɬɢɟ B, ɫɨɫɬɨɹɳɟɟ ɢɥɢ ɢɡ ɨɞɧɨɝɨ ɭɫɩɟɯɚ, ɢɥɢ ɢɡ ɞɜɭɯ, ɢɥɢ ɢɡ ɬɪɟɯ, ɢɥɢ ɢɡ ɱɟɬɵɪɟɯ. ɗɬɢ ɭɫɩɟɯɢ ɧɟɫɨɜɦɟɫɬɧɵ, ɢ ɩɨɬɨɦɭ
P(B) |
P1 |
P2 |
P3 |
P4 |
P0 |
P1 |
P2 |
P3 |
P4 |
P0 |
|||||
|
4 |
|
4 |
4 |
·4 |
4 |
|
4 |
4 |
4 |
4 |
4 |
4 |
||
|
|
4 |
|
§ 1 |
80 |
|
|
|
|
|
|
||||
|
1 q |
1 ¨ |
|
¸ |
|
|
|
#0.987. |
|
|
|
||||
|
|
81 |
|
|
|
||||||||||
|
|
|
|
©3 ¹ |
|
|
|
|
|
|
|||||
ɗɬɨɬ ɠɟ ɪɟɡɭɥɶɬɚɬ ɦɨɠɧɨ ɩɨɥɭɱɢɬɶ ɢ ɛɟɡ ɢɫɩɨɥɶɡɨɜɚɧɢɹ ɫɥɟɞɫɬɜɢɹ 2 ɢɡ ɮɨɪɦɭɥɵ Ȼɟɪɧɭɥɥɢ. Ⱦɟɣɫɬɜɢɬɟɥɶɧɨ, ɟɫɥɢ ɫɨɛɵɬɢɟ B – «ɯɨɬɹ ɛɵ ɨɞɢɧ ɪɚɡ», ɬɨ ɫɨɛɵɬɢɟ ºB — ɷɬɨ «ɧɢ ɨɞɧɨɝɨ ɪɚɡɚ». ȿɝɨ ɜɟɪɨɹɬɧɨɫɬɶ
P(ºB) q4. Ɂɧɚɱɢɬ, P(B) 1 q4.
ɉɨɫɥɟɞɧɢɣ ɩɪɢɦɟɪ ɢɥɥɸɫɬɪɢɪɭɟɬ ɩɪɢɧɰɢɩ ɰɟɥɟɫɨɨɛɪɚɡɧɨɫɬɢ ɩɪɢɦɟɧɟɧɢɹ ɜ ɬɟɨɪɢɢ ɜɟɪɨɹɬɧɨɫɬɟɣ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɝɨ ɫɨɛɵɬɢɹ. ȿɝɨ ɦɨɠɧɨ ɫɮɨɪɦɭɥɢɪɨɜɚɬɶ ɬɚɤ.
ȿɫɥɢ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɟ ɫɨɛɵɬɢɟ ɪɚɫɩɚɞɚɟɬɫɹ ɧɚ ɦɟɧɶɲɟɟ ɱɢɫɥɨ ɜɚɪɢɚɧɬɨɜ, ɱɟɦ ɩɪɹɦɨɟ, ɬɨ ɩɪɢ ɜɵɱɢɫɥɟɧɢɢ ɜɟɪɨɹɬɧɨɫɬɟɣ ɢɦɟɟɬ ɫɦɵɫɥ ɩɟɪɟɣɬɢ ɤ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɦɭ ɫɨɛɵɬɢɸ.
ȼɨɩɪɨɫɵ ɢ ɡɚɞɚɱɢ ɞɥɹ ɫɚɦɨɤɨɧɬɪɨɥɹ
1.ɋɮɨɪɦɭɥɢɪɨɜɚɬɶ ɩɪɚɜɢɥɨ ɭɦɧɨɠɟɧɢɹ ɤɨɦɛɢɧɚɬɨɪɢɤɢ. ɋɮɨɪɦɭɥɢɪɨɜɚɬɶ ɩɪɚɜɢɥɨ ɫɥɨɠɟɧɢɹ ɤɨɦɛɢɧɚɬɨɪɢɤɢ.
2.ɋɮɨɪɦɭɥɢɪɨɜɚɬɶ ɩɨɧɹɬɢɟ «ɩɟɪɟɫɬɚɧɨɜɤɚ» ɢ ɡɚɩɢɫɚɬɶ ɮɨɪɦɭɥɭ ɜɵɱɢɫɥɟɧɢɹ ɨɛɳɟɝɨ ɱɢɫɥɚ ɩɟɪɟɫɬɚɧɨɜɨɤ ɢɡ n ɷɥɟɦɟɧɬɨɜ.
ɋɮɨɪɦɭɥɢɪɨɜɚɬɶ ɩɨɧɹɬɢɟ «ɪɚɡɦɟɳɟɧɢɟ» ɢ ɡɚɩɢɫɚɬɶ ɮɨɪɦɭɥɭ ɜɵɱɢɫɥɟɧɢɹ ɨɛɳɟɝɨ ɱɢɫɥɚ ɪɚɡɦɟɳɟɧɢɣ ɢɡ n ɩɨ k.
ɋɮɨɪɦɭɥɢɪɨɜɚɬɶ ɩɨɧɹɬɢɟ «ɫɨɱɟɬɚɧɢɟ» ɢ ɡɚɩɢɫɚɬɶ ɮɨɪɦɭɥɭ ɜɵɱɢɫɥɟɧɢɹ ɨɛɳɟɝɨ ɱɢɫɥɚ ɫɨɱɟɬɚɧɢɣ ɢɡ n ɩɨ k.
3.Ⱥɧɤɟɬɚ ɩɨ ɢɡɭɱɟɧɢɸ ɨɛɳɟɫɬɜɟɧɧɨɝɨ ɦɧɟɧɢɹ ɫɨɞɟɪɠɢɬ 6 ɜɨɩɪɨɫɨɜ, ɧɚ ɤɚɠɞɵɣ ɢɡ ɤɨɬɨɪɵɯ ɦɨɠɧɨ ɞɚɬɶ ɨɞɢɧ ɢɡ ɬɪɟɯ ɨɬɜɟɬɨɜ: ɞɚ,
112
ɧɟɬ, ɧɟ ɡɧɚɸ. ɇɚɣɬɢ ɨɛɳɟɟ ɱɢɫɥɨ ɜɨɡɦɨɠɧɵɯ ɜɚɪɢɚɧɬɨɜ ɡɚɩɨɥɧɟɧɢɹ ɚɧɤɟɬɵ. ɋɤɨɥɶɤɨ ɫɪɟɞɢ ɧɢɯ ɚɧɤɟɬ, ɤɨɬɨɪɵɟ ɫɨɞɟɪɠɚɬ ɬɨɥɶɤɨ ɪɚɡɧɵɟ ɨɬɜɟɬɵ?
4.ɇɚ ɡɚɧɹɬɢɢ 10 ɫɬɭɞɟɧɬɨɜ. ɉɪɟɩɨɞɚɜɚɬɟɥɶ ɦɨɠɟɬ ɨɩɪɨɫɢɬɶ ɥɸɛɨɟ ɱɢɫɥɨ ɫɬɭɞɟɧɬɨɜ, ɚ ɦɨɠɟɬ ɧɟ ɨɩɪɨɫɢɬɶ ɧɢ ɨɞɧɨɝɨ. ɋɤɨɥɶɤɨ ɫɭɳɟɫɬɜɭɟɬ ɜɚɪɢɚɧɬɨɜ ɞɥɹ ɱɢɫɥɚ ɨɩɪɨɲɟɧɧɵɯ ɫɬɭɞɟɧɬɨɜ, ɟɫɥɢ ɧɢɤɬɨ ɢɡ ɧɢɯ ɧɟ ɨɩɪɚɲɢɜɚɟɬɫɹ ɩɨɜɬɨɪɧɨ, ɩɨɪɹɞɨɤ ɨɩɪɨɫɚ – ɩɪɨɢɡɜɨɥɟɧ?
5.ɋɮɨɪɦɭɥɢɪɨɜɚɬɶ ɩɨɧɹɬɢɹ «ɫɥɭɱɚɣɧɵɣ ɷɤɫɩɟɪɢɦɟɧɬ», «ɫɥɭɱɚɣɧɨɟ ɫɨɛɵɬɢɟ», «ɷɥɟɦɟɧɬɚɪɧɨɟ ɫɨɛɵɬɢɟ», «ɩɪɨɫɬɪɚɧɫɬɜɨ ɷɥɟɦɟɧɬɚɪɧɵɯ ɫɨɛɵɬɢɣ», «ɞɨɫɬɨɜɟɪɧɨɟ ɫɨɛɵɬɢɟ», «ɧɟɜɨɡɦɨɠɧɨɟ ɫɨɛɵɬɢɟ».
6.Ⱦɜɨɟ ɢɝɪɚɸɬ ɜ ɲɚɯɦɚɬɵ. ɋɨɛɵɬɢɟ A – ɜɵɢɝɪɚɥ ɩɟɪɜɵɣ ɢɝɪɨɤ, ɫɨɛɵɬɢɟ B – ɜɵɢɝɪɚɥ ɜɬɨɪɨɣ. ɑɬɨ ɨɡɧɚɱɚɸɬ ɡɚɩɢɫɢ:
ɚ) ºB, |
ɛ) ºAuºB, |
ɜ) ºA ºB? |
7.ɋɮɨɪɦɭɥɢɪɨɜɚɬɶ ɤɥɚɫɫɢɱɟɫɤɨɟ ɨɩɪɟɞɟɥɟɧɢɟ ɜɟɪɨɹɬɧɨɫɬɢ.
8.ȼ ɭɪɧɟ 9 ɤɪɚɫɧɵɯ ɢ 6 ɫɢɧɢɯ ɲɚɪɨɜ. ɇɚɭɝɚɞ ɜɵɧɢɦɚɸɬ ɨɞɢɧ. Ʉɚɤɨɜɚ ɜɟɪɨɹɬɧɨɫɬɶ ɜɵɧɭɬɶ ɤɪɚɫɧɵɣ ɲɚɪ?
9.ɒɢɮɪ ɡɚɦɤɚ ɫɟɣɮɚ ɧɚɛɢɪɚɸɬ ɢɡ ɰɢɮɪ {1,2,3,4,5}. Ⱦɥɢɧɚ ɤɨɞɚ – 4 ɪɚɡɪɹɞɚ. ɉɪɟɫɬɭɩɧɢɤ ɩɵɬɚɟɬɫɹ ɨɬɤɪɵɬɶ ɫɟɣɮ. Ʉɚɤɨɜɚ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɨɧ ɭɝɚɞɚɟɬ ɲɢɮɪ ɫ ɩɟɪɜɨɣ ɩɨɩɵɬɤɢ?
10.ȼ ɭɱɟɛɧɨɣ ɝɪɭɩɩɟ 25 ɫɬɭɞɟɧɬɨɜ. ɂɡ ɧɢɯ 5 ɫɬɭɞɟɧɬɨɜ ɨɬɥɢɱɧɢɤɢ, 10 – ɯɨɪɨɲɢɫɬɵ. ɂɡ ɝɪɭɩɩɵ ɧɚɭɝɚɞ ɜɵɛɢɪɚɸɬ ɨɞɧɨɝɨ ɫɬɭɞɟɧɬɚ ɧɚ ɬɟɫɬɢɪɨɜɚɧɢɟ ɩɨ ɦɚɬɟɦɚɬɢɤɟ. Ʉɚɤɨɜɚ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɜɵɛɪɚɧ ɨɬɥɢɱɧɢɤ ɢɥɢ ɯɨɪɨɲɢɫɬ?
11.ɋɮɨɪɦɭɥɢɪɨɜɚɬɶ ɬɟɨɪɟɦɭ ɭɦɧɨɠɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ. Ɉɩɪɟɞɟɥɢɬɶ ɩɨɧɹɬɢɟ ɭɫɥɨɜɧɨɣ ɜɟɪɨɹɬɧɨɫɬɢ.
12.ȼ ɸɪɢɞɢɱɟɫɤɨɦ ɤɨɥɥɟɞɠɟ ɷɤɡɚɦɟɧ ɩɨ ɦɚɬɟɦɚɬɢɤɟ ɫɞɚɸɬ ɬɚɤ. Ʉɚɠɞɵɣ ɫɬɭɞɟɧɬ ɧɚɭɝɚɞ ɜɵɛɢɪɚɟɬ 5 ɜɨɩɪɨɫɨɜ ɢɡ 25. ɉɨɥɨɠɢɬɟɥɶɧɚɹ ɨɰɟɧɤɚ ɜɵɫɬɚɜɥɹɟɬɫɹ ɩɪɢ ɨɬɜɟɬɟ ɧɚ ɬɪɢ ɢ ɛɨɥɟɟ ɜɨɩɪɨɫɨɜ. ɋɬɭɞɟɧɬ ɋɭɯɨɜ ɜɵɭɱɢɥ 15 ɜɨɩɪɨɫɨɜ. ȼɵɱɢɫɥɢɬɶ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɨɧ:
ɚ) ɩɨɥɭɱɢɬ ɩɹɬɟɪɤɭ, ɛ) ɩɨɥɭɱɢɬ ɩɨɥɨɠɢɬɟɥɶɧɭɸ ɨɰɟɧɤɭ, ɜ) ɧɟ ɫɞɚɫɬ ɷɤɡɚɦɟɧ.
13. ȼ ɬɟɱɟɧɢɟ ɦɟɫɹɰɚ ɫɭɞ ɜɵɧɟɫ 30 ɩɪɢɝɨɜɨɪɨɜ, ɜ ɬɨɦ ɱɢɫɥɟ 6 – ɩɨ ɞɟɥɚɦ ɨ ɤɪɚɠɟ. ȼ ɩɨɪɹɞɤɟ ɩɪɨɤɭɪɨɪɫɤɨɝɨ ɧɚɞɡɨɪɚ ɩɪɨɜɟɪɹɟɬɫɹ 10% ɞɟɥ. Ʉɚɤɨɜɚ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɫɪɟɞɢ ɧɢɯ ɨɤɚɠɟɬɫɹ:
ɚ) ɞɜɚ ɞɟɥɚ ɨ ɤɪɚɠɟ, ɛ) ɯɨɬɹ ɛɵ ɨɞɧɨ ɞɟɥɨ ɨ ɤɪɚɠɟ?
14. Ɂɚɩɢɫɚɬɶ ɮɨɪɦɭɥɭ ɩɨɥɧɨɣ ɜɟɪɨɹɬɧɨɫɬɢ ɢ ɩɨɹɫɧɢɬɶ, ɤɨɝɞɚ ɨɧɚ ɩɪɢɦɟɧɹɟɬɫɹ.
113
15.Ʉɚɤɨɜɚ ɜɟɪɨɹɬɧɨɫɬɶ ɜɵɩɚɞɟɧɢɹ ɯɨɬɹ ɛɵ ɞɜɭɯ ɲɟɫɬɟɪɨɤ ɜ ɬɪɟɯ ɛɪɨɫɤɚɯ ɢɝɪɚɥɶɧɨɝɨ ɤɭɛɢɤɚ?
16.Ɂɚɩɢɫɚɬɶ ɮɨɪɦɭɥɭ Ȼɚɣɟɫɚ ɢ ɩɨɹɫɧɢɬɶ, ɤɨɝɞɚ ɨɧɚ ɩɪɢɦɟ-
ɧɹɟɬɫɹ.
17.ɋɨɛɵɬɢɟ «ɜɵɩɚɥɨ ɯɨɬɹ ɛɵ ɞɜɟ ɲɟɫɬɟɪɤɢ» ɢɡ ɩ. 16 ɧɚɫɬɭɩɢɥɨ. Ʉɚɤɨɜɚ ɜɟɪɨɹɬɧɨɫɬɶ ɩɪɟɞɩɨɥɨɠɟɧɢɹ ɨ ɬɨɦ, ɱɬɨ ɷɬɨ ɛɵɥɨ «ɪɨɜɧɨ ɞɜɟ ɲɟɫɬɟɪɤɢ»?
18.ɉɨɹɫɧɢɬɶ, ɤɚɤɨɣ ɫɥɭɱɚɣɧɵɣ ɷɤɫɩɟɪɢɦɟɧɬ ɨɬɜɟɱɚɟɬ ɫɯɟɦɟ Ȼɟɪɧɭɥɥɢ? Ɂɚɩɢɫɚɬɶ ɮɨɪɦɭɥɭ Ȼɟɪɧɭɥɥɢ.
19.Ʉɚɠɞɵɣ ɱɟɬɜɟɪɬɵɣ ɤɥɢɟɧɬ ɛɚɧɤɚ ɩɪɢɯɨɞɢɬ ɜ ɛɚɧɤ ɛɪɚɬɶ ɩɪɨɰɟɧɬɵ ɫ ɜɤɥɚɞɚ. ɋɟɣɱɚɫ ɜ ɛɚɧɤɟ ɨɠɢɞɚɸɬ ɫɜɨɟɣ ɨɱɟɪɟɞɢ ɧɚ ɨɛɫɥɭɠɢɜɚɧɢɟ 6 ɤɥɢɟɧɬɨɜ. ɇɚɣɬɢ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɢɡ ɧɢɯ ɛɭɞɭɬ ɛɪɚɬɶ ɩɪɨɰɟɧɬɵ ɚ) ɬɨɥɶɤɨ ɞɜɨɟ, ɛ) ɯɨɬɹ ɛɵ ɨɞɢɧ.
20.ȼɟɪɨɹɬɧɨɫɬɶ ɩɨɩɚɞɚɧɢɹ ɜ ɦɢɲɟɧɶ ɩɪɢ ɨɞɧɨɦ ɜɵɫɬɪɟɥɟ ɪɚɜɧɚ 0.2. ɋɤɨɥɶɤɨ ɜɵɫɬɪɟɥɨɜ ɧɭɠɧɨ ɩɪɨɢɡɜɟɫɬɢ, ɱɬɨɛɵ ɫ ɜɟɪɨɹɬɧɨɫɬɶɸ
0.9ɩɨɪɚɡɢɬɶ ɦɢɲɟɧɶ ɯɨɬɹ ɛɵ ɨɞɢɧ ɪɚɡ?
Глава 8. Случайные величины
8.1. Понятие случайной величины
ɇɟɪɟɞɤɨ ɪɟɡɭɥɶɬɚɬɨɦ ɫɥɭɱɚɣɧɨɝɨ ɷɤɫɩɟɪɢɦɟɧɬɚ ɹɜɥɹɟɬɫɹ ɱɢɫɥɨɜɚɹ ɜɟɥɢɱɢɧɚ, ɡɧɚɱɟɧɢɟ ɤɨɬɨɪɨɣ ɜ ɤɚɠɞɨɦ ɷɤɫɩɟɪɢɦɟɧɬɟ ɪɚɡɧɨɟ. Ɍɚɤɚɹ ɜɟɥɢɱɢɧɚ ɧɚɡɵɜɚɟɬɫɹ ɫɥɭɱɚɣɧɨɣ. ɇɚɩɪɢɦɟɪ,
ɱɢɫɥɨ ɩɨɩɚɞɚɧɢɣ ɜ ɦɢɲɟɧɶ ɩɪɢ ɬɪɟɯ ɜɵɫɬɪɟɥɚɯ ɦɨɠɟɬ ɩɪɢɧɢɦɚɬɶ ɨɞɧɨ ɢɡ ɫɥɟɞɭɸɳɢɯ ɡɧɚɱɟɧɢɣ: 0, 1, 2, 3;
ɩɨɤɚɡɚɧɢɹ ɦɟɞɢɰɢɧɫɤɨɝɨ ɬɟɪɦɨɦɟɬɪɚ ɩɪɢ ɢɡɦɟɪɟɧɢɢ ɬɟɦɩɟɪɚɬɭɪɵ ɩɚɰɢɟɧɬɚ ɩɪɢɧɢɦɚɸɬ ɨɞɧɨ ɢɡ ɫɥɟɞɭɸɳɢɯ ɡɧɚɱɟɧɢɣ: 34.1, 34.2,…,36.7,…,42.0 ɝɪɚɞɭɫɨɜ.
ȼɩɟɪɜɨɦ ɩɪɢɦɟɪɟ ɦɢɧɢɦɚɥɶɧɨɟ ɪɚɫɫɬɨɹɧɢɟ ɦɟɠɞɭ ɫɨɫɟɞɧɢɦɢ ɡɧɚɱɟɧɢɹɦɢ (ɨɬɫɱɟɬɚɦɢ) ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ ɪɚɜɧɨ ɟɞɢɧɢɰɟ, ɜɨ ɜɬɨɪɨɦ – 0.1 ɝɪɚɞɭɫɚ. Ȼɵɜɚɸɬ ɫɥɭɱɚɣɧɵɟ ɜɟɥɢɱɢɧɵ ɢ ɫ ɛɨɥɶɲɢɦɢ, ɢ ɦɟɧɶɲɢɦɢ ɪɚɫɫɬɨɹɧɢɹɦɢ ɦɟɠɞɭ ɨɬɫɱɟɬɚɦɢ.
ɋɥɭɱɚɣɧɵɟ ɜɟɥɢɱɢɧɵ, ɭ ɤɨɬɨɪɵɯ ɪɚɫɫɬɨɹɧɢɟ ɦɟɠɞɭ ɫɨɫɟɞɧɢɦɢ ɨɬɫɱɟɬɚɦɢ – ɜɟɥɢɱɢɧɚ ɤɨɧɟɱɧɚɹ, ɧɚɡɵɜɚɸɬɫɹ ɞɢɫɤɪɟɬɧɵɦɢ. Ɉɛɵɱɧɨ ɧɚɛɨɪ ɡɧɚɱɟɧɢɣ ɭ ɞɢɫɤɪɟɬɧɵɯ ɜɟɥɢɱɢɧ ɤɨɧɟɱɟɧ (ɤɚɤ ɜ ɩɪɢɜɟɞɟɧɧɵɯ ɩɪɢɦɟɪɚɯ).
ȼɨɛɳɟɦ ɫɥɭɱɚɟ, ɞɢɫɤɪɟɬɧɵɟ ɫɥɭɱɚɣɧɵɟ ɜɟɥɢɱɢɧɵ – ɱɢɫɥɚ ɪɚɰɢɨɧɚɥɶɧɵɟ. ɇɚ ɱɢɫɥɨɜɨɣ ɩɪɹɦɨɣ ɨɧɢ ɩɪɟɞɫɬɚɜɥɟɧɵ ɬɨɱɤɚɦɢ, ɤɨɬɨɪɵɟ ɪɚɡɞɟɥɟɧɵ ɤɨɧɟɱɧɵɦɢ ɩɪɨɦɟɠɭɬɤɚɦɢ, ɚ ɞɥɢɧɚ ɤɚɠɞɨɝɨ ɢɡ ɩɪɨɦɟɠɭɬɤɨɜ ɪɚɜɧɚ ɟɞɢɧɢɰɟ ɦɥɚɞɲɟɝɨ ɪɚɡɪɹɞɚ ɜ ɡɚɩɢɫɢ ɷɬɢɯ ɱɢɫɟɥ.
114
ȼ ɫɥɭɱɚɣɧɵɯ ɷɤɫɩɟɪɢɦɟɧɬɚɯ ɞɟɣɫɬɜɭɸɬ ɢ ɫɨ ɫɥɭɱɚɣɧɵɦɢ ɜɟɥɢɱɢɧɚɦɢ ɞɪɭɝɨɣ ɩɪɢɪɨɞɵ. ɇɚɩɪɢɦɟɪ,
ɜɟɫ ɧɚɭɝɚɞ ɜɡɹɬɨɝɨ ɨɫɤɨɥɤɚ ɛɨɦɛɵ,
ɨɲɢɛɤɚ ɜ ɢɡɦɟɪɟɧɢɢ ɫɤɨɪɨɫɬɢ ɞɜɢɠɟɧɢɹ ɚɜɬɨɦɨɛɢɥɹ.
ȼɨɡɦɨɠɧɵɟ ɡɧɚɱɟɧɢɹ ɤɚɠɞɨɣ ɢɡ ɬɚɤɢɯ ɜɟɥɢɱɢɧ ɨɞɧɨ ɨɬ ɞɪɭɝɨɝɨ ɧɟ ɨɬɞɟɥɟɧɵ, ɢ ɨɛɪɚɡɭɸɬ ɧɚ ɱɢɫɥɨɜɨɣ ɩɪɹɦɨɣ ɫɩɥɨɲɧɨɣ ɦɚɫɫɢɜ ɬɨɱɟɤ. Ⱥ ɷɬɨ ɜɟɳɟɫɬɜɟɧɧɵɟ ɱɢɫɥɚ.
ɋɥɭɱɚɣɧɵɟ ɜɟɥɢɱɢɧɵ, ɭ ɤɨɬɨɪɵɯ ɡɧɚɱɟɧɢɹ – ɫɭɬɶ ɜɟɳɟɫɬɜɟɧɧɵɟ ɱɢɫɥɚ, ɧɚɡɵɜɚɸɬɫɹ ɧɟɩɪɟɪɵɜɧɵɦɢ. ȼ ɨɛɳɟɦ ɫɥɭɱɚɟ, ɜɨɡɦɨɠɧɵɣ ɧɚɛɨɪ ɡɧɚɱɟɧɢɣ ɧɟɩɪɟɪɵɜɧɨɣ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ – ɜɫɹ ɱɢɫɥɨɜɚɹ ɩɪɹɦɚɹ. Ɋɚɛɨɬɚɸɬ ɢ ɫ ɬɚɤɢɦɢ ɧɟɩɪɟɪɵɜɧɵɦɢ ɫɥɭɱɚɣɧɵɦɢ ɜɟɥɢɱɢɧɚɦɢ, ɡɧɚɱɟɧɢɹ ɤɨɬɨɪɵɯ – ɨɬɪɟɡɨɤ ɧɚ ɱɢɫɥɨɜɨɣ ɩɪɹɦɨɣ.
ȿɫɥɢ ɤɥɚɫɫɢɱɟɫɤɚɹ ɬɟɨɪɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ ɢɦɟɟɬ ɞɟɥɨ ɩɨ ɩɪɟɢɦɭɳɟɫɬɜɭ ɫ ɫɨɛɵɬɢɹɦɢ ɧɟɱɢɫɥɨɜɨɣ ɩɪɢɪɨɞɵ, ɬɨ ɫɨɜɪɟɦɟɧɧɚɹ ɬɟɨɪɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ ɨɩɟɪɢɪɭɟɬ ɫ ɱɢɫɥɚɦɢ – ɫɥɭɱɚɣɧɵɦɢ ɜɟɥɢɱɢɧɚɦɢ. ɗɬɨ ɫɬɪɟɦɹɬɫɹ ɞɟɥɚɬɶ ɞɚɠɟ ɢ ɬɨɝɞɚ, ɤɨɝɞɚ ɪɟɡɭɥɶɬɚɬɨɦ ɫɥɭɱɚɣɧɨɝɨ ɷɤɫɩɟɪɢɦɟɧɬɚ ɱɢɫɥɨ ɧɟ ɹɜɥɹɟɬɫɹ.
ɇɚɩɪɢɦɟɪ, ɩɪɨɜɨɞɢɬɫɹ ɨɩɵɬ, ɜ ɪɟɡɭɥɶɬɚɬɟ ɤɨɬɨɪɨɝɨ ɦɨɠɟɬ ɧɚɫɬɭɩɢɬɶ ɢɥɢ ɧɟ ɧɚɫɬɭɩɢɬɶ ɫɨɛɵɬɢɟ A. ɋɨɛɵɬɢɸ A ɦɨɠɧɨ ɫɨɩɨɫɬɚɜɢɬɶ ɱɢɫɥɨ X, ɤɨɬɨɪɨɟ ɩɪɢɧɢɦɚɟɬ ɡɧɚɱɟɧɢɟ 1 ɩɪɢ ɧɚɫɬɭɩɥɟɧɢɢ A, ɢ ɨɧɨ ɪɚɜɧɨ 0, ɤɨɝɞɚ A ɧɟ ɧɚɫɬɭɩɢɥɨ. Ɍɟɩɟɪɶ X – ɞɢɫɤɪɟɬɧɚɹ ɫɥɭɱɚɣɧɚɹ ɜɟɥɢɱɢɧɚ, ɤɨɬɨɪɚɹ ɯɚɪɚɤɬɟɪɢɡɭɟɬ ɫɨɛɵɬɢɟ A. ȼɨɡɦɨɠɧɵɟ ɟɟ ɡɧɚɱɟɧɢɹ –
{0,1}.
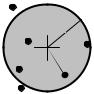
ȿɳɟ ɩɪɢɦɟɪ. ɋɨɛɵɬɢɟ B – ɩɨɩɚɞɚɧɢɟ ɩɪɢ ɫɬɪɟɥɶɛɟ ɜ ɤɪɭɝɥɭɸ ɦɢɲɟɧɶ (ɪɢɫ. 8.1). Ɉɛɨɡɧɚɱɢɦ ɪɚɞɢɭɫ ɤɪɭɝɚ ɤɚɤ r, ɚ ɪɚɫɫɬɨɹɧɢɟ ɨɬ ɰɟɧɬɪɚ ɦɢɲɟɧɢ ɞɨ ɬɨɱɤɢ ɩɨɩɚɞɚɧɢɹ ɩɭɥɢ ɤɚɤ R. Ɍɨɝɞɚ ɧɚɫɬɭɩɥɟɧɢɸ ɫɨɛɵɬɢɹ B ɨɬɜɟɱɚɟɬ ɜɵɩɨɥɧɟɧɢɟ ɧɟɪɚɜɟɧɫɬɜɚ R r, ɬɨ ɟɫɬɶ ɜɟɪɨɹɬɧɨɫɬɶ ɫɨɛɵɬɢɹ B – ɧɟ ɱɬɨ ɢɧɨɟ, ɤɚɤ ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ ɷɬɨ ɧɟɪɚɜɟɧɫɬɜɨ ɜɵɩɨɥɧɹɟɬɫɹ.
ɂɬɚɤ, ɜ ɫɨɜɪɟɦɟɧɧɨɣ ɬɟɨɪɢɢ ɜɟɪɨɹɬɧɨɫɬɟɣ, ɝɞɟ ɬɨɥɶɤɨ ɜɨɡɦɨɠɧɨ, ɨɬ ɫɯɟɦɵ ɫɥɭɱɚɣɧɵɯ ɫɨɛɵɬɢɣ ɩɟɪɟɯɨɞɹɬ ɤ ɫɯɟɦɟ ɫɥɭɱɚɣɧɵɯ ɜɟɥɢɱɢɧ. ɗɬɚ ɫɯɟɦɚ ɩɪɟɞɨɫɬɚɜɥɹɟɬ ɞɥɹ ɪɟɲɟɧɢɹ ɡɚɞɚɱ, ɨɬɧɨɫɹɳɢɯɫɹ ɤ ɫɥɭɱɚɣɧɵɦ ɹɜɥɟɧɢɹɦ, ɛɨɥɟɟ ɝɢɛɤɢɣ ɢ ɭɧɢɜɟɪɫɚɥɶɧɵɣ ɚɩɩɚɪɚɬ ɦɚɬɟɦɚɬɢɤɢ.
8.2. Ɂɚɤɨɧɵ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɫɥɭɱɚɣɧɵɯ ɜɟɥɢɱɢɧ
Ɂɚɤɨɧɨɦɟɪɧɨɫɬɶ, ɤɨɬɨɪɚɹ ɭɫɬɚɧɚɜɥɢɜɚɟɬ ɫɜɹɡɶ ɦɟɠɞɭ ɜɨɡɦɨɠɧɵɦɢ ɡɧɚɱɟɧɢɹɦɢ ɬɨɣ ɢɥɢ ɢɧɨɣ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ ɋȼ ɢ ɜɟɪɨɹɬɧɨɫɬɹɦɢ ɷɬɢɯ ɡɧɚɱɟɧɢɣ, ɧɚɡɵɜɚɸɬ ɡɚɤɨɧɨɦ ɟɟ ɪɚɫɩɪɟɞɟɥɟɧɢɹ.
115
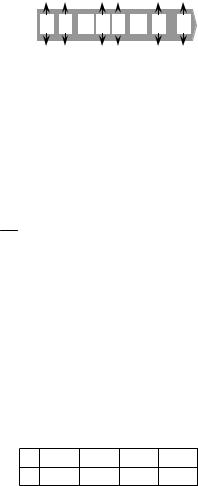
ɂɡɭɱɟɧɢɟ ɡɚɤɨɧɨɜ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɧɚɱɧɟɦ ɫ ɞ ɢ ɫ ɤ ɪ ɟ ɬ ɧ ɵ ɯ ɫɥɭɱɚɣɧɵɯ ɜɟɥɢɱɢɧ.
Ɋɹɞ ɪɚɫɩɪɟɞɟɥɟɧɢɹ. Ɉɛɨɡɧɚɱɢɦ ɞɢɫɤɪɟɬɧɭɸ ɋȼ ɤɚɤ X, ɚ ɧɚɛɨɪ ɟɟ ɨɬɫɱɟɬɨɜ – ɤɚɤ x0, x1,…, xn. ɂɫɯɨɞ ɫɥɭɱɚɣɧɨɝɨ ɷɤɫɩɟɪɢɦɟɧɬɚ – ɫɨɛɵɬɢɟ X xk ɯɚɪɚɤɬɟɪɢɡɭɟɬɫɹ ɜɟɪɨɹɬɧɨɫɬɶɸ P(X xk) pk. Ɏɚɤɬ ɪɚɜɟɧɫɬɜɚ ɱɢɫɟɥ X xk ɭɫɬɚɧɚɜɥɢɜɚɸɬ ɩɭɬɟɦ ɩɨɫɥɟɞɨɜɚɬɟɥɶ-
ɧɨɝɨ ɫɪɚɜɧɟɧɢɹ ɰɢɮɪ ɜ ɨɞɧɨɢɦɟɧɧɵɯ ɪɚɡɪɹɞɚɯ ɡɚɩɢɫɟɣ X ɢ xk (ɫɦ. ɫɩɪɚɜɚ). ȿɫɥɢ ɢɦɟɟɬ ɦɟɫɬɨ ai bi ɞɥɹ ɜɫɟɯ i r,r 1, , m, ɬɨ ɱɢɫɥɚ X ɢ xk ɪɚɜɧɵ.
ɋɨɩɨɫɬɚɜɢɦ ɤɚɠɞɨɦɭ ɨɬɫɱɟɬɭ xk ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ X ɜɟɪɨɹɬɧɨɫɬɶ pk. ȼ ɪɟɡɭɥɶɬɚɬɟ ɩɨɥɭɱɢɦ ɡɚɤɨɧ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɞɢɫɤɪɟɬɧɨɣ ɋȼ X. ɋɚɦɨɣ ɩɪɨɫɬɨɣ ɮɨɪɦɨɣ ɡɚɩɢɫɢ ɡɚɤɨɧɚ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɞɢɫɤɪɟɬɧɨɣ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ ɹɜɥɹɟɬɫɹ ɬɚɛɥɢɰɚ, ɜ ɩɟɪɜɨɣ ɫɬɪɨɤɟ ɤɨɬɨɪɨɣ ɩɟɪɟɱɢɫɥɹɸɬɫɹ ɟɟ ɨɬɫɱɟɬɵ xk, ɚ ɜɨ ɜɬɨɪɨɣ — ɜɟɪɨɹɬɧɨɫɬɢ pk. Ɍɚɤɭɸ ɬɚɛɥɢɰɭ {xk,pk} ɢ ɧɚɡɵɜɚɸɬ ɪɹɞɨɦ ɪɚɫɩɪɟɞɟɥɟɧɢɹ.
Ɉɱɟɜɢɞɧɨ, ɱɬɨ ɫɨɛɵɬɢɹ X xk, k 0,n ɨɛɪɚɡɭɸɬ ɩɨɥɧɭɸ ɝɪɭɩɩɭ, ɢ
n
¦pk 1.
k 1
ɉɪɢɦɟɪ. ɋɬɪɟɥɨɤ ɩɪɨɢɡɜɨɞɢɬ ɬɪɢ ɜɵɫɬɪɟɥɚ ɩɨ ɦɢɲɟɧɢ. ȼɟɪɨɹɬɧɨɫɬɶ ɩɨɩɚɞɚɧɢɹ ɜ ɦɢɲɟɧɶ ɩɪɢ ɤɚɠɞɨɦ ɜɵɫɬɪɟɥɟ ɪɚɜɧɚ 0.6. ɉɨɫɬɪɨɢɬɶ ɪɹɞ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɞɥɹ ɱɢɫɥɚ ɩɨɩɚɞɚɧɢɣ ɜ ɦɢɲɟɧɶ ɩɪɢ ɬɪɟɯ ɜɵɫɬɪɟɥɚɯ.
Ɋɟɲɟɧɢɟ. Ɉɛɨɡɧɚɱɢɦ ɤɚɤ Z ɞɢɫɤɪɟɬɧɭɸ ɫɥɭɱɚɣɧɭɸ ɜɟɥɢɱɢɧɭ – ɱɢɫɥɨ ɩɨɩɚɞɚɧɢɣ ɜ ɦɢɲɟɧɶ. ɇɚɛɨɪ ɟɟ ɡɧɚɱɟɧɢɣ: z0 0, z1 1, z2 2, z3 3. Ɉɩɵɬ ɭɤɥɚɞɵɜɚɟɬɫɹ ɜ ɫɯɟɦɭ Ȼɟɪɧɭɥɥɢ. ɉɨɷɬɨɦɭ ɜɟɪɨɹɬɧɨɫɬɶ ɫɨɛɵɬɢɹ Z zk ɜɵɱɢɫɥɹɟɦ ɩɨ ɮɨɪɦɭɥɟ Ȼɟɪɧɭɥɥɢ:
p0 P30 0.43 0.064,
p1 P31 C13 u0.6u0,42 0.288, p2 P32 C32 u0.62u0.4 0.432,
p3 P33 0.63 0.216.
Ɍɚɛɥɢɰɚ 8.1
zk 0 |
1 |
2 |
3 |
pk 0.064 0.288 0.432 0.216
Ɍɟɩɟɪɶ ɫɨɫɬɚɜɥɹɟɦ ɬɚɛɥ.8.1 – ɪɹɞ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ Z.
Ɂɚɤɨɧ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɞɥɹ ɧɟɩɪɟɪɵɜɧɵɯ ɋȼ ɡɚɞɚɟɬɫɹ ɥɢɛɨ ɮɭɧɤɰɢɟɣ ɪɚɫɩɪɟɞɟɥɟɧɢɹ, ɥɢɛɨ ɩɥɨɬɧɨɫɬɶɸ ɪɚɫɩɪɟɞɟɥɟɧɢɹ.
116
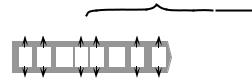
Ɏɭɧɤɰɢɹ ɪɚɫɩɪɟɞɟɥɟɧɢɹ. ɇɚɩɨɦɧɢɦ, ɱɬɨ ɧɟɩɪɟɪɵɜɧɚɹ ɋȼ X – ɱɢɫɥɨ ɜɟɳɟɫɬɜɟɧɧɨɟ. Ɍɨɱɧɨ ɬɚɤ ɢ ɜɨɡɦɨɠɧɨɟ ɟɟ ɡɧɚɱɟɧɢɟ ɜɟɥɢɱɢɧɚ x – ɬɨɱɤɚ ɜ ɫɩɥɨɲɧɨɦ ɦɚɫɫɢɜɟ ɬɨɱɟɤ ɧɚ ɱɢɫɥɨɜɨɣ ɨɫɢ ɬɨɠɟ ɱɢɫɥɨ ɜɟɳɟɫɬɜɟɧɧɨɟ. ȼ ɡɚɩɢɫɢ ɤɚɠɞɨɝɨ ɜɟɳɟɫɬɜɟɧɧɨɝɨ ɱɢɫɥɚ ɞɪɨɛɧɚɹ ɱɚɫɬɶ ɢɦɟɟɬ ɛɟɫɤɨɧɟɱɧɭɸ ɞɥɢɧɭ. ɉɨɷɬɨɦɭ ɞɥɹ ɜɟɳɟɫɬɜɟɧɧɵɯ ɱɢɫɟɥ ɧɟɥɶɡɹ
ɭɫɬɚɧɨɜɢɬɶ ɮɚɤɬ ɢɯ ɪɚ-
fɜɟɧɫɬɜɚ ɜ ɫɢɥɭ ɬɨɝɨ, ɱɬɨ
ɩɪɨɰɟɞɭɪɭ ɩɨɫɥɟɞɨɜɚ-
ɬɟɥɶɧɨɝɨ ɫɪɚɜɧɟɧɢɹ ɰɢɮɪ X ar ar 1 a0.a 1 a i 1 a i a m 1 a m ɜ ɨɞɧɨɢɦɟɧɧɵɯ ɪɚɡɪɹɞɚɯ
ɡɚɩɢɫɟɣ ɡɚɜɟɪɲɢɬɶ ɧɟ-
|
|
z |
|
ɜɨɡɦɨɠɧɨ. Ɂɚɬɨ |
ɩɭɬɟɦ |
|
|
|
|
|
|||
|
|
|
|
ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɝɨ |
ɫɪɚɜ- |
|
x br br 1 |
b0.b 1 |
b i 1 b i |
b m 1 b m |
|||
ɧɟɧɢɹ ɰɢɮɪ ɜ ɨɞɧɨɢɦɟɧ- |
||||||
|
|
|
|
ɧɵɯ ɪɚɡɪɹɞɚɯ ɷɬɢɯ |
ɡɚɩɢ- |
|
ɫɟɣ ɦɨɠɧɨ ɭɫɬɚɧɨɜɢɬɶ ɮɚɤɬ ajzbj (ɫɦ. ɫɥɟɜɚ), ɚ ɡɧɚɱɢɬ, ɢ ɮɚɤɬ Xzx. ɇɚ ɷɬɨɦ ɩɪɨɰɟɞɭɪɚ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɝɨ ɫɪɚɜɧɟɧɢɹ ɰɢɮɪ ɜ ɨɞɧɨɢɦɟɧɧɵɯ ɪɚɡɪɹɞɚɯ ɡɚɩɢɫɟɣ X ɢ x ɡɚɜɟɪɲɚɟɬɫɹ.
ɉɪɢ ɩɨɫɬɪɨɟɧɢɢ ɡɚɤɨɧɚ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɧɟɩɪɟɪɵɜɧɨɣ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ X ɨɩɟɪɢɪɭɸɬ ɫ ɫɨɛɵɬɢɟɦ X x. ɗɬɨ ɧɟɪɚɜɟɧɫɬɜɨ ɦɨɠɧɨ ɡɚɮɢɤɫɢɪɨɜɚɬɶ ɩɭɬɟɦ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɝɨ ɫɪɚɜɧɟɧɢɹ ɰɢɮɪ ɜ ɨɞɧɨɢɦɟɧɧɵɯ ɪɚɡɪɹɞɚɯ ɡɚɩɢɫɟɣ X ɢ x. ɇɚɩɨɦɧɢɦ, ɱɬɨ ɡɞɟɫɶ X – ɪɟɡɭɥɶɬɚɬ ɫɥɭɱɚɣɧɨɝɨ ɷɤɫɩɟɪɢɦɟɧɬɚ, ɚ x – ɥɸɛɚɹ ɬɨɱɤɚ ɧɚ ɱɢɫɥɨɜɨɣ ɩɪɹɦɨɣ, ɬɨ ɟɫɬɶ x ɹɜɥɹɟɬɫɹ ɧɟɡɚɜɢɫɢɦɨɣ ɩɟɪɟɦɟɧɧɨɣ. Ɂɧɚɱɢɬ, ɜɟɪɨɹɬɧɨɫɬɶ ɫɨɛɵɬɢɹ X x ɟɫɬɶ ɧɟɤɨɬɨɪɚɹ ɮɭɧɤɰɢɹ ɩɟɪɟɦɟɧɧɨɣ x. ɗɬɭ ɮɭɧɤɰɢɸ ɢ ɧɚɡɵɜɚɸɬ
ɮ ɭ ɧ ɤ ɰ ɢ ɟ ɣ ɪ ɚ ɫ ɩ ɪ ɟ ɞ ɟ ɥ ɟ ɧ ɢ ɹ |
ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ X ɢ ɨɛɨ- |
|
ɡɧɚɱɚɸɬ ɤɚɤ F(x): |
|
|
F(x) P(X x). |
(8.1) |
|
ɉɪɟɠɞɟ ɱɟɦ ɞɜɢɝɚɬɶɫɹ ɞɚɥɶɲɟ, ɨɬɦɟɬɢɦ ɝɥɭɛɨɤɢɣ ɮɢɥɨɫɨɮ- |
||
ɫɤɢɣ ɫɦɵɫɥ |
ɷɬɨɝɨ ɨɩɪɟɞɟɥɟɧɢɹ. ȼ |
ɥɟɜɨɣ ɱɚɫɬɢ (8.1) ɡɚɩɢɫɚɧɚ |
ɮ ɭ ɧ ɤ ɰ ɢ ɹ |
ɞɟɣɫɬɜɢɬɟɥɶɧɨɝɨ ɚɪɝɭɦɟɧɬɚ, ɚ ɜ ɩɪɚɜɨɣ – ɜ ɟ ɪ ɨ ɹ ɬ - |
|
ɧ ɨ ɫ ɬ ɶ ɧɟɤɨɬɨɪɨɝɨ ɫɨɛɵɬɢɹ. Ɏɭɧɤɰɢɹ ɹɜɥɹɟɬɫɹ ɨɞɧɢɦ ɢɡ ɮɭɧɞɚɦɟɧɬɚɥɶɧɵɯ ɩɨɧɹɬɢɣ ɦɚɬɟɦɚɬɢɱɟɫɤɨɝɨ ɚɧɚɥɢɡɚ, ɬɨɣ ɨɛɥɚɫɬɢ ɦɚɬɟɦɚɬɢɤɢ, ɝɞɟ ɢɡɭɱɚɸɬɫɹ ɠɟɫɬɤɨ ɨɩɪɟɞɟɥɟɧɧɵɟ ɡɚɤɨɧɨɦɟɪɧɨɫɬɢ. ȼɟɪɨɹɬɧɨɫɬɶ – ɮɭɧɞɚɦɟɧɬɚɥɶɧɨɟ ɩɨɧɹɬɢɟ ɬɟɨɪɢɢ ɜɟɪɨɹɬɧɨɫɬɟɣ, ɤɨɬɨɪɚɹ ɢɡɭɱɚɟɬ ɡɚɤɨɧɨɦɟɪɧɨɫɬɢ ɜ ɦɢɪɟ ɫɥɭɱɚɣɧɨɝɨ. Ɏɨɪɦɭɥɚ (8.1) ɩɟɪɟɛɪɚɫɵɜɚɟɬ ɦɨɫɬ ɦɟɠɞɭ ɦɚɬɟɦɚɬɢɱɟɫɤɢɦ ɚɧɚɥɢɡɨɦ ɢ ɬɟɨɪɢɟɣ ɜɟɪɨɹɬɧɨɫɬɟɣ. Ɍɟɦ ɫɚɦɵɦ ɫɬɪɨɝɢɣ, ɯɨɪɨɲɨ ɪɚɡɪɚɛɨɬɚɧɧɵɣ ɚɩɩɚɪɚɬ ɦɚɬɟɦɚɬɢɱɟɫɤɨɝɨ ɚɧɚɥɢɡɚ ɫɬɚɧɨɜɢɬɫɹ ɦɨɳɧɵɦ ɢɧɫɬɪɭɦɟɧɬɨɦ ɢɫɫɥɟɞɨɜɚɧɢɹ ɫɥɭɱɚɣɧɵɯ ɜɟɥɢɱɢɧ ɜ ɬɟɨɪɢɢ ɜɟɪɨɹɬɧɨɫɬɟɣ.
ɉɟɪɟɱɢɫɥɢɦ ɨɛɳɢɟ ɫɜɨɣɫɬɜɚ ɮɭɧɤɰɢɢ ɪɚɫɩɪɟɞɟɥɟɧɢɹ.
1.Ɏɭɧɤɰɢɹ F(x) – ɧɟɭɛɵɜɚɸɳɚɹ ɮɭɧɤɰɢɹ ɫɜɨɟɝɨ ɚɪɝɭɦɟɧɬɚ,
ɬɨ ɟɫɬɶ ɩɪɢ x2!x1 ɢ F(x2)tF(x1).
2.F( f) 1.
117
|
|
|
|
|
3. |
F(f) |
0. |
|
|
|
|
|
|
|
|
|
Ʉ ɷɬɢɦ ɫɜɨɣɫɬɜɚɦ ɩɪɢɜɟɞɟɦ ɝɟɨɦɟɬɪɢ- |
||||||
|
|
|
|
ɱɟɫɤɢɟ ɩɨɹɫɧɟɧɢɹ (ɪɢɫ. 8.2). ɉɭɫɬɶ x – ɬɨɱɤɚ |
|||||||
X |
x |
|
ɧɚ ɨɫɢ 0x. ɋɥɭɱɚɣɧɚɹ ɜɟɥɢɱɢɧɚ X ɜ ɪɟɡɭɥɶ- |
||||||||
|
ɬɚɬɟ ɨɩɵɬɚ ɦɨɠɟɬ ɡɚɧɹɬɶ ɧɚ ɷɬɨɣ ɠɟ ɨɫɢ ɬɨ |
||||||||||
|
Ɋɢɫ. 8.2 |
|
ɢɥɢ |
ɢɧɨɟ |
ɩɨɥɨɠɟɧɢɟ. Ɍɨɝɞɚ F(x) P(X x) – |
||||||
|
|
|
|
ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ X ɩɨɩɚɞɟɬ ɜ ɡɨɧɭ ɧɚ |
|||||||
ɨɫɢ ɥɟɜɟɟ ɬɨɱɤɢ x (ɜ ɡɚɲɬɪɢɯɨɜɚɧɧɭɸ ɡɨɧɭ). ɉɪɢ ɭɜɟɥɢɱɟɧɢɢ x ɭɜɟɥɢ- |
|||||||||||
ɱɢɜɚɟɬɫɹ ɡɚɲɬɪɢɯɨɜɚɧɧɚɹ ɨɛɥɚɫɬɶ ɥɟɜɟɟ ɧɟɝɨ. ɉɨɷɬɨɦɭ ɜɟɪɨɹɬɧɨɫɬɶ |
|||||||||||
P(X x) ɭɦɟɧɶɲɢɬɶɫɹ ɧɟ ɦɨɠɟɬ. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, F(x) ɫ ɪɨɫɬɨɦ x ɧɟ |
|||||||||||
ɭɛɵɜɚɟɬ (ɫɜɨɣɫɬɜɨ 1). |
|
|
|
|
|
|
|
|
|||
Ɉɱɟɜɢɞɧɨ, ɱɬɨ ɩɪɢ xo f ɡɚɲɬɪɢɯɨɜɚɧɧɚɹ ɨɛɥɚɫɬɶ ɥɟɜɟɟ x ɫɬɚ- |
|||||||||||
ɧɨɜɢɬɫɹ ɛɟɫɤɨɧɟɱɧɨ ɛɨɥɶɲɨɣ, ɢ ɩɨɩɚɞɚɧɢɟ ɜ ɧɟɟ X ɨɤɚɡɵɜɚɟɬɫɹ ɫɨ- |
|||||||||||
ɛɵɬɢɟɦ |
|
ɞɨɫɬɨɜɟɪɧɵɦ. |
ɉɨɷɬɨɦɭ |
|
F(w) |
|
|
|
|
||
F(f) P(Xf) 1 |
(ɫɜɨɣɫɬɜɨ |
2). |
1 |
|
|
|
|
||||
Ɍɨɱɧɨ ɬɚɤ, ɩɪɢ xo f ɩɨɩɚɞɚɧɢɟ X |
|
|
|
|
|
||||||
ɥɟɜɟɟ x ɫɬɚɧɨɜɢɬɫɹ ɧɟɜɨɡɦɨɠɧɵɦ, |
|
|
|
|
|
P(1 W 3) |
|||||
ɢ F(f) |
P(Xf) |
0 (ɫɜɨɣɫɬɜɨ 3). |
|
|
|
|
|
||||
|
|
|
|
|
|
||||||
ɉɪɢɦɟɪ. Ɏɭɧɤɰɢɹ ɪɚɫɩɪɟɞɟ- |
|
|
|
|
|
|
|||||
ɥɟɧɢɹ |
ɧɟɩɪɟɪɵɜɧɨɣ |
ɫɥɭɱɚɣɧɨɣ |
|
|
|
F(3) |
|
||||
ɜɟɥɢɱɢɧɵ W ɡɚɞɚɧɚ ɮɨɪɦɭɥɨɣ: |
|
|
|
|
|||||||
|
F(1) |
|
|
|
|||||||
|
|
F(w) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
0 |
|
ɩɪɢ w 0, |
|
|
|
|
|
|
|
w |
|
®1 e w |
|
ɩɪɢ w t 0. |
|
|
0 |
1 |
2 |
3 |
4 |
(8.2) |
|
¯ |
|
|
|
|
|
5 |
|||||
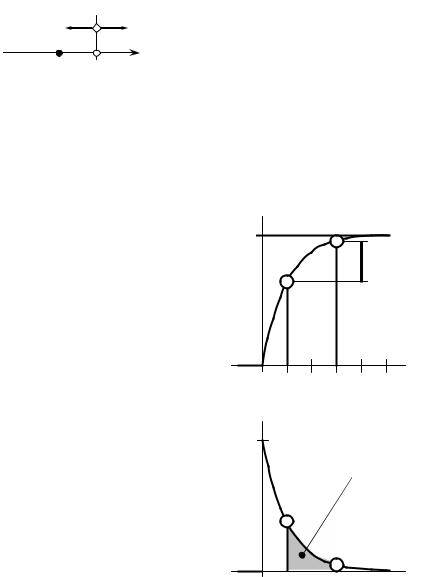
Ƚɪɚɮɢɤ ɷɬɨɣ ɮɭɧɤɰɢɢ ɩɨɤɚɡɚɧ ɧɚ |
|
|
Ɋɢɫ. 8.3 |
|
|
||||||
ɪɢɫ. 8.3. Ʉɚɤ ɜɢɞɢɦ, F(x) ɨɛɥɚɞɚɟɬ |
|
f(w) |
|
|
|
|
|||||
ɜɫɟɦɢ ɭɤɚɡɚɧɧɵɦɢ ɫɜɨɣɫɬɜɚɦɢ. |
1 |
|
|
|
|
||||||
|
|
|
|
|
|||||||
ɉɥɨɬɧɨɫɬɶ |
ɪɚɫɩɪɟɞɟɥɟɧɢɹ. |
|
|
|
|
|
|||||
|
P(1 W 3) |
|
|
||||||||
Ⱦɥɹ ɧɟɩɪɟɪɵɜɧɨɣ ɫɥɭɱɚɣɧɨɣ ɜɟ- |
|
|
|
||||||||
ɥɢɱɢɧɵ X ɮɭɧɤɰɢɹ ɪɚɫɩɪɟɞɟɥɟɧɢɹ |
|
|
|
|
|
|
|||||
F(x) ɧɟɩɪɟɪɵɜɧɚ, ɚ ɡɧɚɱɢɬ, ɢ ɞɢɮ- |
|
|
|
|
|
|
|||||
ɮɟɪɟɧɰɢɪɭɟɦɚ ɧɚ ɜɫɟɣ ɱɢɫɥɨɜɨɣ |
|
|
|
|
|
|
|||||
ɨɫɢ. ɉɪɨɞɢɮɮɟɪɟɧɰɢɪɨɜɚɜ |
F(x), |
|
|
|
|
|
|
||||
ɩɨɥɭɱɢɦ ɮɭɧɤɰɢɸ |
|
|
|
|
|
|
|
|
|||
|
f(x) F’(x), |
|
|
|
|
|
|
(8.3) |
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
w |
ɤɨɬɨɪɚɹ |
ɧɚɡɵɜɚɟɬɫɹ ɩ ɥ ɨ ɬ ɧ ɨ - |
0 |
|
1 |
2 3 4 5 |
|
||||
|
||||||||||
ɫ ɬ ɶ ɸ |
ɪ ɚ ɫ ɩ ɪ ɟ ɞ ɟ ɥ ɟ ɧ ɢ ɹ ɢɥɢ |
|
|
Ɋɢɫ. 8.4 |
||||||
ɩɥɨɬɧɨɫɬɶɸ ɜɟɪɨɹɬɧɨɫɬɢ (ɩɨ ɚɧɚ- |
|
|
|
|
|
|
|
|
||
ɥɨɝɢɢ ɫ ɩɥɨɬɧɨɫɬɶɸ ɜɟɳɟɫɬɜɚ).
118

ɉɪɢɦɟɪ. Ɏɭɧɤɰɢɹ ɪɚɫɩɪɟɞɟɥɟɧɢɹ f(w) ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ, ɭ ɤɨɬɨɪɨɣ F(w) ɡɚɞɚɧɚ ɮɨɪɦɭɥɨɣ (8.2):
f(w) |
0 |
w |
ɩɪɢ w 0, |
® |
(8.4) |
||
|
¯e |
|
ɩɪɢ w t 0. |
ɇɚ ɪɢɫ. 8.4 ɩɨɤɚɡɚɧ ɝɪɚɮɢɤ ɩɥɨɬɧɨɫɬɢ ɪɚɫɩɪɟɞɟɥɟɧɢɹ (8.4). ȿɝɨ ɧɚɡɵɜɚɸɬ ɤɪɢɜɨɣ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɧɟɩɪɟɪɵɜɧɨɣ ɋȼ.
Ɋɚɫɫɦɨɬɪɢɦ ɫɜɨɣɫɬɜɚ ɩɥɨɬɧɨɫɬɢ ɪɚɫɩɪɟɞɟɥɟɧɢɹ.
1.ɉɥɨɬɧɨɫɬɶ ɪɚɫɩɪɟɞɟɥɟɧɢɹ – ɮɭɧɤɰɢɹ ɧɟɨɬɪɢɰɚɬɟɥɶɧɚɹ: f(x)t0 ɞɥɹ fxf
2.ɉɨɥɧɚɹɩɥɨɳɚɞɶɩɨɞɤɪɢɜɨɣɪɚɫɩɪɟɞɟɥɟɧɢɹɪɚɜɧɚɟɞɢɧɢɰɟ:
f
³f(x)udx 1
f
(ɫɨɛɵɬɢɟ fXf ɞɨɫɬɨɜɟɪɧɨ, ɟɝɨ ɜɟɪɨɹɬɧɨɫɬɶ ɪɚɜɧɚ ɟɞɢɧɢɰɟ).
Ɉɬɦɟɬɢɦ ɜɚɠɧɨɟ ɨɛɫɬɨɹɬɟɥɶɫɬɜɨ. ɋɥɭɱɚɣɧɚɹ ɜɟɥɢɱɢɧɚ X ɨɛɵɱɧɨ ɢɦɟɟɬ ɪɚɡɦɟɪɧɨɫɬɶ. Ɉɬɫɱɟɬɵ ɮɭɧɤɰɢɢ F(x) ɪɚɡɦɟɪɧɨɫɬɢ ɧɟ ɢɦɟɸɬ. Ⱥ ɜɨɬ ɨɬɫɱɟɬɵ f(x) ɢɦɟɸɬ ɪɚɡɦɟɪɧɨɫɬɶ, ɨɛɪɚɬɧɭɸ ɪɚɡɦɟɪɧɨɫɬɢ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ X.
Ʉɨɝɞɚ ɡɚɞɚɧɚ ɮɭɧɤɰɢɹ ɪɚɫɩɪɟɞɟɥɟɧɢɹ F(x), ɩɥɨɬɧɨɫɬɶ ɜɟɪɨɹɬɧɨɫɬɢ f(x) ɜɵɱɢɫɥɹɸɬ ɩɨ ɮɨɪɦɭɥɟ (8.3). Ⱥ ɟɫɥɢ ɡɚɞɚɧɚ ɩɥɨɬɧɨɫɬɶ ɪɚɫɩɪɟɞɟɥɟɧɢɹ f(x), ɬɨ ɮɭɧɤɰɢɸ ɪɚɫɩɪɟɞɟɥɟɧɢɹ F(x) ɜɵɱɢɫɥɹɸɬ ɬɚɤ:
x |
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
||
F(x) ³f(s)uds |
(8.5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f |
|
|
|
|
b |
|
||
ɉɨɷɬɨɦɭ ɮɭɧɤɰɢɸ F(x) ɧɚɡɵɜɚɸɬ ɢɧɬɟɝɪɚɥɶɧɵɦ |
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|||
ɡɚɤɨɧɨɦ ɪɚɫɩɪɟɞɟɥɟɧɢɹ, ɚ ɮɭɧɤɰɢɸ f(x) ɧɚɡɵɜɚ- |
|
|
|
|
|
|
|
|
ɸɬ ɞɢɮɮɟɪɟɧɰɢɚɥɶɧɵɦ ɡɚɤɨɧɨɦ ɪɚɫɩɪɟɞɟɥɟɧɢɹ |
a |
|
|
|
|
|
||
ɧɟɩɪɟɪɵɜɧɨɣ ɋȼ. |
|
|
|
|
|
|
|
C |
|
|
|
|
|
||||
ȼɟɪɨɹɬɧɨɫɬɶ ɩɨɩɚɞɚɧɢɹ ɫɥɭɱɚɣɧɨɣ ɜɟ- |
|
|
|
|
|
|
|
|
ɥɢɱɢɧɵ ɜ ɡɚɞɚɧɧɵɣ ɞɢɚɩɚɡɨɧ. Ɂɚɞɚɞɢɦ ɧɚ ɨɫɢ |
a |
|
b |
|
||||
0x ɞɜɟ ɬɨɱɤɢ a, b ɢ ɜɵɱɢɫɥɢɦ ɜɟɪɨɹɬɧɨɫɬɶ ɬɚɤɨɝɨ |
Ɋɢɫ. 8.5 |
|||||||
ɫɨɛɵɬɢɹ adX b, ɚ ɢɦɟɧɧɨ, ɜɟɪɨɹɬɧɨɫɬɶ ɬɨɝɨ, ɱɬɨ
ɫɥɭɱɚɣɧɚɹ ɜɟɥɢɱɢɧɚ X ɜ ɪɟɡɭɥɶɬɚɬɟ ɨɩɵɬɚ ɩɨɩɚɞɟɬ ɜ ɞɢɚɩɚɡɨɧ, ɨɝɪɚ-
ɧɢɱɟɧɧɵɣ ɬɨɱɤɚɦɢ a ɢ b. Ⱦɥɹ ɷɬɨɝɨ ɪɚɫɫɦɨɬɪɢɦ ɬɚɤɢɟ ɫɨɛɵɬɢɹ (ɪɢɫ. 8.5):
A:X b,
B:X a,
119
C: adX b.
ɋɨɛɵɬɢɹ B ɢ C ɧɟɫɨɜɦɟɫɬɧɵ, ɬɚɤ ɤɚɤ X ɧɟ ɦɨɠɟɬ ɨɤɚɡɚɬɶɫɹ ɨɞɧɨɜɪɟɦɟɧɧɨ ɢ ɫɥɟɜɚ, ɢ ɫɩɪɚɜɚ ɨɬ ɬɨɱɤɢ a. ɋɨɛɵɬɢɟ A – ɫɭɦɦɚ ɫɨɛɵɬɢɣ B ɢ C: A B C (ɪɢɫ. 8.5). ɉɨ ɮɨɪɦɭɥɟ ɫɥɨɠɟɧɢɹ ɜɟɪɨɹɬɧɨɫɬɟɣ ɞɥɹ ɧɟɫɨɜɦɟɫɬɧɵɯ ɫɥɭɱɚɣɧɵɯ ɫɨɛɵɬɢɣ ɢɦɟɟɦ:
P(X b) P(X a) P(adX b)
ɢɥɢ ɫ ɭɱɟɬɨɦ ɨɩɪɟɞɟɥɟɧɢɹ (8.1)
F(b) F(a) P(adX b).
Ɉɬɤɭɞɚ ɫɥɟɞɭɟɬ, ɱɬɨ
P(adX b) F(b) F(a). |
(8.6) |
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɜɟɪɨɹɬɧɨɫɬɶ ɩɨɩɚɞɚɧɢɹ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ ɜ ɡɚɞɚɧɧɵɣ ɞɢɚɩɚɡɨɧ ɪɚɜɧɚ ɩɪɢɪɚɳɟɧɢɸ ɟɟ ɮɭɧɤɰɢɢ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɧɚ ɷɬɨɦ ɞɢɚɩɚɡɨɧɟ.
ɍɤɚɠɟɦ ɧɚ ɥɸɛɨɩɵɬɧɨɟ ɫɥɟɞɫɬɜɢɟ ɢɡ ɮɨɪɦɭɥɵ (8.3). ɉɭɫɬɶ X – ɧɟɩɪɟɪɵɜɧɚɹ ɫɥɭɱɚɣɧɚɹ ɜɟɥɢɱɢɧɚ. Ȼɭɞɟɦ ɧɟɨɝɪɚɧɢɱɟɧɧɨ ɭɦɟɧɶɲɚɬɶ ɪɚɡɦɟɪ ɞɢɚɩɚɡɨɧɚ ɩɭɬɟɦ boa. ȼ ɪɟɡɭɥɶɬɚɬɟ ɩɨɥɭɱɢɦ ɫɨɛɵɬɢɟ X a, ɜɟɪɨɹɬɧɨɫɬɶ ɤɨɬɨɪɨɝɨ ɟɫɬɶ
P(x a) lim P a d X b |
lim F b F(a) 0. |
boa |
boa |
Ʉɚɤ ɜɢɞɢɦ, ɜɟɪɨɹɬɧɨɫɬɶ ɨɬɞɟɥɶɧɨɝɨ ɬɨɱɟɱɧɨɝɨ ɡɧɚɱɟɧɢɹ ɧɟɩɪɟɪɵɜɧɨɣ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ ɪɚɜɧɚ ɧɭɥɸ! Ⱦɪɭɝɢɦɢ ɫɥɨɜɚɦɢ, ɞɥɹ ɧɟɩɪɟɪɵɜɧɨɣ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ ɜɟɪɨɹɬɧɨɫɬɶ ɫɨɛɵɬɢɹ X a ɪɚɜɧɚ ɧɭɥɸ, ɧɨ ɫɨɛɵɬɢɟ ɷɬɨ ɜɨɡɦɨɠɧɨ (ɪɟɡɭɥɶɬɚɬ ɫɥɭɱɚɣɧɨɝɨ ɷɤɫɩɟɪɢɦɟɧɬɚ X ɦɨɠɟɬ ɩɨɩɚɫɬɶ ɜ ɬɨɱɤɭ a ɧɚ ɱɢɫɥɨɜɨɣ ɩɪɹɦɨɣ). ɉɨɫɤɨɥɶɤɭ P(X a) 0, ɧɟɪɚɜɟɧɫɬɜɚ adX b ɷɤɜɢɜɚɥɟɧɬɧɵ ɧɟɪɚɜɟɧɫɬɜɚɦ a X b. ɗɬɢ ɫɬɪɨɝɢɟ ɧɟɪɚɜɟɧɫɬɜɚ ɢ ɢɫɩɨɥɶɡɭɸɬ ɩɪɢ ɜɵɱɢɫɥɟɧɢɢ ɜɟɪɨɹɬɧɨɫɬɢ ɩɨɩɚɞɚɧɢɹ ɫɥɭɱɚɣɧɨɣ ɜɟɥɢɱɢɧɵ ɜ ɡɚɞɚɧɧɵɣ ɞɢɚɩɚɡɨɧ (ɜ ɢɧɬɟɪɜɚɥ ]a,b[).
ɉɪɢɦɟɪ. ȼɵɱɢɫɥɢɬɶ ɜɟɪɨɹɬɧɨɫɬɶ ɩɨɩɚɞɚɧɢɹ ɋȼ W ɜ ɞɢɚɩɚɡɨɧ ɨɬ a 1 b 3.
Ʉɨɝɞɚ ɡɚɞɚɧɚ F(x), ɞɟɣɫɬɜɭɟɦ ɩɨ ɮɨɪɦɭɥɟ (8.6), ɜ ɤɨɬɨɪɨɣ ɧɟɫɬɪɨɝɨɟ ɧɟɪɚɜɟɧɫɬɜɨ adX ɡɚɦɟɧɢɦ ɫɬɪɨɝɢɦ a X:
P(1 W 3) F(3) F(1) 0.95 0.63 0.32.
ɉɪɢɪɚɳɟɧɢɟ ɮɭɧɤɰɢɢ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɧɚ ɢɧɬɟɪɜɚɥɟ ]1,3[, ɚ ɢɦɟɧɧɨ,
ɱɢɫɥɨ F(3) F(1) P(1 W 3) 0.32, ɩɨɤɚɡɚɧɨ ɧɚ ɪɢɫ. 8.3.
Ʉɨɝɞɚ ɡɚɞɚɧɚ ɩɥɨɬɧɨɫɬɶ ɪɚɫɩɪɟɞɟɥɟɧɢɹ f(x), ɜɟɪɨɹɬɧɨɫɬɶ ɫɨɛɵɬɢɹ a X b ɜɵɱɢɫɥɹɟɬɫɹ ɬɚɤ:
120
