
Математика для юристов - Д.А. Ловцова
.pdfɧɚɧɟɫ ɭɳɟɪɛ ɟɝɨ ɞɟɥɨɜɨɣ ɪɟɩɭɬɚɰɢɢ. Ɍɨɝɞɚ x1 x0 – ɷɬɨ ɢɥɢ ɞɟɣɫɬɜɢɟ x1, ɢɥɢ ɞɟɣɫɬɜɢɟ x0, ɢɥɢ ɢ ɬɨ ɢ ɞɪɭɝɨɟ ɜɦɟɫɬɟ (ɢ ɜɫɟ ɨɧɢ ɪɟɝɭɥɢɪɭɸɬɫɹ ɫɬ. 4 Ɂɚɤɨɧɚ ɨ ɤɨɧɤɭɪɟɧɰɢɢ).
Ⱦɢɡɴɸɧɤɰɢɹ n ɩɟɪɟɦɟɧɧɵɯ ɡɚɩɢɫɵɜɚɟɬɫɹ ɬɚɤ:
y xn-1 xn-2 x0.
Ɋɟɡɭɥɶɬɚɬɨɦ ɥɸɛɨɣ ɢɡ ɪɚɫɫɦɨɬɪɟɧɧɵɯ ɥɨɝɢɱɟɫɤɢɯ ɨɩɟɪɚɰɢɣ ɦɨɠɟɬ ɛɵɬɶ ɢɥɢ 0, ɢɥɢ 1. Ɂɧɚɱɢɬ, ɪɟɡɭɥɶɬɚɬ ɨɞɧɨɣ ɥɨɝɢɱɟɫɤɨɣ ɨɩɟɪɚɰɢɢ ɦɨɠɟɬ ɜɵɫɬɭɩɚɬɶ ɨɩɟɪɚɧɞɨɦ ɜ ɞɪɭɝɨɣ. Ɍɚɤ ɦɨɠɧɨ ɫɨɫɬɚɜɢɬɶ ɫɭɩɟɪɩɨɡɢɰɢɢ ɥɨɝɢɱɟɫɤɢɯ ɨɩɟɪɚɰɢɣ (ɥɨɝɢɱɟɫɤɢɟ ɮɨɪɦɭɥɵ) ɢ ɢɡ ɩɪɨɫɬɵɯ ɜɵɫɤɚɡɵɜɚɧɢɣ ɫɨɫɬɚɜɥɹɬɶ ɫɥɨɠɧɵɟ. ɉɪɢ ɷɬɨɦ ɫɥɟɞɭɟɬ ɪɭɤɨɜɨɞɫɬɜɨɜɚɬɶɫɹ ɩɪɚɜɢɥɨɦ ɨ ɩɪɢɨɪɢɬɟɬɚɯ ɥɨɝɢɱɟɫɤɢɯ ɨɩɟɪɚɰɢɣ. ɗɬɢ ɩɪɢɨɪɢɬɟɬɵ ɭɛɵɜɚɸɬ ɜ ɬɚɤɨɦ ɩɨɪɹɞɤɟ: ɇȿ, ɂ, ɂɅɂ, ɚ ɬɪɟɛɭɟɦɵɣ ɩɨɪɹɞɨɤ ɜɵɱɢɫɥɟɧɢɣ, ɧɚɪɭɲɚɸɳɢɣ ɩɪɚɜɢɥɨ ɨ ɩɪɢɨɪɢɬɟɬɚɯ, ɡɚɞɚɸɬ ɫɤɨɛɤɚɦɢ. ɇɚɩɪɢɦɟɪ,
y º((x1ºx0) (ºx1 x0)).
Ɋɚɡɪɚɛɨɬɚɟɦ ɬɚɛɥɢɰɭ ɢɫɬɢɧɧɨɫɬɢ ɞɥɹ ɷɬɨɣ ɮɨɪɦɭɥɵ (ɬɚɛɥ.2.4), ɜ ɤɨɬɨɪɨɣ ɫɧɚɱɚɥɚ ɜɵɱɢɫɥɢɦ ɡɧɚɱɟɧɢɹ ɞɜɭɯ ɞɢɡɴɸɧɤɰɢɣ (x1ºx0) ɢ (ºx1 x0), ɩɨɬɨɦ ɢɯ ɤɨɧɴɸɧɤɰɢɸ ɢ, ɧɚɤɨɧɟɰ, ɢɧɜɟɪɫɢɸ ɷɬɨɣ ɤɨɧɴɸɧɤɰɢɢ. Ɍɚɤ ɩɨɥɭɱɢɦ ɡɧɚɱɟɧɢɹ ɫɥɨɠɧɨɝɨ ɜɵɫɤɚɡɵɜɚɧɢɹ y ɞɥɹ ɩɨɥɧɨɝɨ ɧɚɛɨɪɚ ɜɫɟɯ ɡɧɚɱɟɧɢɣ ɜɵɫɤɚɡɵɜɚɧɢɣ-ɚɪɝɭɦɟɧɬɨɜ x1 ɢ x0.
|
|
|
|
|
Ɍɚɛɥɢɰɚ 2.4 |
x1 |
x0 |
x1ºx0 |
ºx1 x0 |
(x1ºx0) (ºx1 x0) |
º((x1ºx0) (ºx1 x0)) |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
Ɉɬɪɢɰɚɧɢɟ, ɤɨɧɴɸɧɤɰɢɹ ɢ ɞɢɡɴɸɧɤɰɢɹ ɨɛɪɚɡɭɸɬ ɮɭɧɤɰɢɨɧɚɥɶɧɨ ɩɨɥɧɭɸ ɫɢɫɬɟɦɭ ɨɩɟɪɚɰɢɣ ɦɚɬɟɦɚɬɢɱɟɫɤɨɣ ɥɨɝɢɤɢ.
Ʌɸɛɭɸ ɞɪɭɝɭɸ ɥɨɝɢɱɟɫɤɭɸ ɨɩɟɪɚɰɢɸ ɦɨɠɧɨ ɩɪɟɞɫɬɚɜɢɬɶ ɫɭɩɟɪɩɨɡɢɰɢɟɣ ɷɬɢɯ ɨɩɟɪɚɰɢɣ. Ɍɟɦ ɧɟ ɦɟɧɟɟ ɩɪɢɜɟɞɟɦ ɟɳɟ ɞɜɟ ɥɨɝɢɱɟɫɤɢɟ ɨɩɟɪɚɰɢɢ, ɤɨɬɨɪɵɟ ɢɦɟɸɬ ɫɚɦɨɫɬɨɹɬɟɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɜ ɚɥɝɟɛɪɟ ɜɵɫɤɚɡɵɜɚɧɢɣ.
ɂɦɩɥɢɤɚɰɢɹ – ɞɜɭɦɟɫɬɧɚɹ ɨɩɟɪɚɰɢɹ. Ɉɧɚ ɡɚɞɚɟɬɫɹ ɬɚɛɥ.2.5, ɚ ɡɚɩɢɫɵɜɚɟɬɫɹ ɤɚɤ
y x1ox0.
21
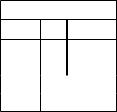
ɉɪɚɜɚɹ ɱɚɫɬɶ ɷɬɨɣ ɡɚɩɢɫɢ ɱɢɬɚɟɬɫɹ ɬɚɤ: ɟɫɥɢ x1, ɬɨ x0, ɯɨɬɹ ɜ ɢɦɩɥɢɤɚɰɢɢ ɦɟɠɞɭ x1 ɢ x0 ɧɢɤɚɤɨɣ ɩɪɢɱɢɧ- ɧɨ-ɫɥɟɞɫɬɜɟɧɧɨɣ ɢɥɢ ɫɦɵɫɥɨɜɨɣ ɫɜɹɡɢ ɧɟɬ. ɉɪɨɫɬɨ ɢɡ ɞɜɭɯ ɜɵɫɤɚɡɵɜɚɧɢɣ x1 ɢ x0 ɫɨɫɬɚɜɥɹɟɬɫɹ ɧɨɜɨɟ ɜɵɫɤɚɡɵɜɚɧɢɟ y ɩɨ ɩɪɚɜɢɥɚɦ, ɤɨɬɨɪɵɟ ɡɚɞɚɧɵ ɬɚɛɥ.2.5. ȼ ɢɦɩɥɢɤɚɰɢɢ ɩɟɪɟɦɟɧɧɚɹ x1 ɧɚɡɵɜɚɟɬɫɹ ɩɨɫɵɥɤɨɣ, ɚ x0 – ɡɚɤɥɸɱɟɧɢɟɦ. ɂɡ ɬɚɛɥ.2.5 ɜɢɞɧɨ, ɱɬɨ ɢɦɩɥɢɤɚɰɢɹ ɩɪɢɧɢɦɚɟɬ ɡɧɚɱɟɧɢɟ 0 (ɥɨɠɶ)
Ɍɚɛɥɢɰɚ 2.5
x1 |
x0 |
|
y |
0 |
0 |
1 |
ɞɚ |
0 |
1 |
1 |
ɞɚ |
1 |
0 |
0 |
ɧɟɬ |
1 |
1 |
1 |
ɞɚ |
ɬɨɥɶɤɨ ɧɚ ɨɞɧɨɦ ɧɚɛɨɪɟ, ɚ ɢɦɟɧɧɨ ɤɨɝɞɚ x1 1 (ɩɨ-
ɫɵɥɤɚ ɢɫɬɢɧɧɚ), ɚ x0 0 (ɡɚɤɥɸɱɟɧɢɟ ɥɨɠɧɨ). ɇɚ ɨɫɬɚɥɶɧɵɯ ɧɚɛɨɪɚɯ ɟɟ ɡɧɚɱɟɧɢɟ ɪɚɜɧɨ 1 (ɢɫɬɢɧɚ). ɗɬɨ ɩɪɨɳɟ ɡɚɩɨɦɢɧɚɟɬɫɹ, ɟɫɥɢ ɡɧɚɱɟɧɢɹ ɢɦɩɥɢɤɚɰɢɢ 1 ɢ 0 ɡɚɦɟɧɢɬɶ ɧɚ ɢɯ ɷɤɜɢɜɚɥɟɧɬɵ: ɧɟɬ ɢ ɞɚ (ɬɚɛɥ. 2.5).
Ʌɨɝɢɱɟɫɤɭɸ ɤɨɧɫɬɪɭɤɰɢɸ ɢɦɩɥɢɤɚɰɢɢ ɢɦɟɸɬ ɦɚɬɟɦɚɬɢɱɟɫɤɢɟ ɬɟɨɪɟɦɵ. ɇɚɩɪɢɦɟɪ,
«ȿɫɥɢ ɞɜɚ ɭɝɥɚ ɜɟɪɬɢɤɚɥɶɧɵ, ɬɨ ɨɧɢ ɪɚɜɧɵ».
Ɂɞɟɫɶ x1 – ɞɜɚ ɭɝɥɚ ɜɟɪɬɢɤɚɥɶɧɵ, x0 – ɨɧɢ ɪɚɜɧɵ. ȼɟɪɧɨɫɬɢ ɬɟɨɪɟɦɵ ɨɬɜɟɱɚɟɬ ɩɨɫɥɟɞɧɹɹ ɫɬɪɨɤɚ ɬɚɛɥ.2.5. ɍɬɜɟɪɠɞɟɧɢɟ «ȿɫɥɢ ɞɜɚ ɭɝɥɚ ɜɟɪɬɢɤɚɥɶɧɵ, ɬɨ ɨɧɢ ɧɟ ɪɚɜɧɵ» – ɥɨɠɧɨ, ɚ ɷɬɨ – ɬɪɟɬɶɹ ɫɬɪɨɤɚ ɬɚɛɥ.2.5. ɍɬɜɟɪɠɞɟɧɢɹ «ȿɫɥɢ ɞɜɚ ɭɝɥɚ ɧɟ ɜɟɪɬɢɤɚɥɶɧɵ, ɬɨ ɨɧɢ ɪɚɜɧɵ» (ɫɬɪɨɤɚ ɜɬɨɪɚɹ ɬɚɛɥ.2.5) ɢ «ȿɫɥɢ ɞɜɚ ɭɝɥɚ ɧɟ ɜɟɪɬɢɤɚɥɶɧɵ, ɬɨ ɨɧɢ ɧɟ ɪɚɜɧɵ» (ɩɟɪɜɚɹ ɫɬɪɨɤɚ ɬɚɛɥ.2.5) ɦɨɝɭɬ ɛɵɬɶ ɢɫɬɢɧɧɵɦɢ ɢɥɢ ɥɨɠɧɵɦɢ, ɧɨ ɜ ɢɦɩɥɢɤɚɰɢɢ ɩɨɞɨɛɧɵɟ ɭɬɜɟɪɠɞɟɧɢɹ ɨɞɧɨɡɧɚɱɧɨ ɨɩɪɟɞɟɥɟɧɵ ɤɚɤ ɢɫɬɢɧɧɵɟ.
ȼ ɸɪɢɞɢɱɟɫɤɢɯ ɞɨɤɭɦɟɧɬɚɯ ɮɨɪɦɭ ɢɦɩɥɢɤɚɰɢɣ ɢɦɟɸɬ ɩɪɚɜɨɜɵɟ ɩɪɟɞɩɢɫɚɧɢɹ, ɧɚɩɪɢɦɟɪ (ɀɄ ɊɎ, ɫɬ. 79, ɱ.6):
Ɍɚɛɥɢɰɚ 2.6
x1 x0 ºx1 ºx1 x0
0 0 1 1 ɞɚ
0 1 1 1 ɞɚ
1 0 0 
 0 ɧɟɬ
0 ɧɟɬ
1 1 0 
 1 ɞɚ
1 ɞɚ
«ȿɫɥɢ ɞɨɝɨɜɨɪ ɩɨɞɧɚɣɦɚ ɡɚɤɥɸɱɟɧ ɛɟɡ ɭɤɚɡɚɧɢɹ ɫɪɨɤɚ, ɧɚɧɢɦɚɬɟɥɶ ɨɛɹɡɚɧ ɩɪɟɞɭɩɪɟɞɢɬɶ ɩɨɞɧɚɧɢɦɚɬɟɥɹ ɨ ɩɪɟɤɪɚɳɟɧɢɢ ɞɨɝɨɜɨɪɚ ɩɨɞɧɚɣɦɚ ɡɚ ɬɪɢ ɦɟɫɹɰɚ».
Ɂɚɩɢɲɟɦ ɢɦɩɥɢɤɚɰɢɸ ɜ ɬɟɪɦɢɧɚɯ ɮɭɧɤɰɢɨɧɚɥɶɧɨ ɩɨɥɧɨɣ ɫɢɫɬɟɦɵ ɨɩɟɪɚɰɢɣ:
x1ox0 ºx1 x0.
ȼ ɜɟɪɧɨɫɬɢ ɷɬɨɝɨ ɪɚɜɟɧɫɬɜɚ ɭɛɟɞɢɦɫɹ, ɩɨɫɬɪɨɢɜ ɬɚɛɥɢɰɭ ɢɫɬɢɧɧɨɫɬɢ (ɬɚɛɥ.2.6) ɞɥɹ ɩɪɚɜɨɣ ɟɝɨ ɱɚɫɬɢ ɢ ɫɪɚɜɧɢɜ ɟɟ
ɜɵɯɨɞ ɫ ɜɵɯɨɞɨɦ ɬɚɛɥ.2.5. ɉɪɢ ɩɨɫɬɪɨɟɧɢɢ ɬɚɛɥ.2.6 ɦɵ ɢɫɩɨɥɶɡɨɜɚ-
ɥɢ ɬɚɛɥ. 2.1 ɢ ɬɚɛɥ.2.3.
ɗɤɜɢɜɚɥɟɧɬɧɨɫɬɶ – ɦɧɨɝɨɦɟɫɬɧɚɹ ɨɩɟɪɚɰɢɹ. Ⱦɥɹ ɞɜɭɯ ɩɟɪɟɦɟɧɧɵɯ ɨɧɚ ɡɚɞɚɟɬɫɹ ɬɚɛɥ.2.7, ɚ ɡɚɩɢɫɵɜɚɟɬɫɹ ɬɚɤ:
y (x1 x0).
22
ɉɪɚɜɚɹ ɱɚɫɬɶ ɷɬɨɣ ɡɚɩɢɫɢ ɱɢɬɚɟɬɫɹ ɬɚɤ: |
Ɍɚɛɥɢɰɚ 2.7 |
||||
x1 ɬɨɝɞɚ ɢ ɬɨɥɶɤɨ ɬɨɝɞɚ, ɤɨɝɞɚ x0. |
x1 |
x0 |
y |
||
ɋɢɧɨɧɢɦɵ ɞɥɹ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɢ: |
0 |
0 |
1 |
||
x1 |
ɜ ɬɨɦ, ɢ ɬɨɥɶɤɨ ɜ ɬɨɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ |
0 |
1 |
0 |
|
x0; |
|
1 |
0 |
0 |
|
ɟɫɬɶ ɧɟɨɛɯɨɞɢɦɨɟ ɢ ɞɨɫɬɚɬɨɱɧɨɟ ɭɫ- |
1 |
1 |
1 |
||
x1 |
|||||
ɥɨɜɢɟ ɞɥɹ x0; |
|
|
|
|
|
x0 ɟɫɬɶ ɧɟɨɛɯɨɞɢɦɨɟ ɢ ɞɨɫɬɚɬɨɱɧɨɟ ɭɫɥɨɜɢɟ ɞɥɹ x1. ɟɫɥɢ x1, ɬɨ x0, ɂ ɟɫɥɢ x0, ɬɨ x1;
Ʉɚɤ ɜɢɞɢɦ, ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɶ ɪɚɜɧɚ 1 (ɢɫɬɢɧɧɚ) ɬɨɝɞɚ, ɤɨɝɞɚ ɟɟ ɚɪɝɭɦɟɧɬɵ ɩɪɢɧɢɦɚɸɬ ɨɞɢɧɚɤɨɜɵɟ ɡɧɚɱɟɧɢɹ – ɢɥɢ ɜɫɟ ɪɚɜɧɵ 0 (ɥɨɠɧɵ), ɢɥɢ ɜɫɟ ɪɚɜɧɵ 1 (ɢɫɬɢɧɧɵ). ɉɨɷɬɨɦɭ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɶ ɧɚɡɵɜɚɸɬ ɟɳɟ ɪɚɜɧɨɡɧɚɱɧɨɫɬɶɸ ɢ ɨɛɨɡɧɚɱɚɸɬ ɫɢɦɜɨɥɨɦ .
Ʌɸɛɨɟ ɪɚɜɟɧɫɬɜɨ, ɟɫɥɢ ɟɝɨ ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɤɚɤ ɨɞɧɨ ɜɵɫɤɚɡɵɜɚɧɢɟ, ɹɜɥɹɟɬɫɹ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɶɸ. ɇɚɩɪɢɦɟɪ, «ȼɫɟ ɟɞɢɧɨ, ɱɬɨ ɜ ɥɨɛ, ɱɬɨ ɩɨ ɥɛɭ».
ɗɤɜɢɜɚɥɟɧɬɧɨɫɬɶ n ɩɟɪɟɦɟɧɧɵɯ ɡɚɩɢɫɵɜɚɟɬɫɹ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚ-
ɡɨɦ:
y (xn-1 xn-2 |
x0). |
ȼ ɬɟɪɦɢɧɚɯ ɮɭɧɤɰɢɨɧɚɥɶɧɨ ɩɨɥɧɨɣ ɫɢɫɬɟɦɵ ɨɩɟɪɚɰɢɣ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɶ ɞɜɭɯ ɩɟɪɟɦɟɧɧɵɯ ɡɚɩɢɫɵɜɚɟɬɫɹ ɬɚɤ:
(x1 x0) ºx1ºx0 x1 x0.
ɋɨɫɬɚɜɢɦ ɬɚɛɥɢɰɭ ɢɫɬɢɧɧɨɫɬɢ ɞɥɹ ɩɪɚɜɨɣ ɱɚɫɬɢ ɷɬɨɣ ɮɨɪɦɭɥɵ (ɬɚɛɥ.2.8), ɫɪɚɜɧɢɦ ɟɟ ɜɵɯɨɞ ɫ ɜɵɯɨɞɨɦ ɬɚɛɥ.2.7 ɢ ɭɛɟɞɢɦɫɹ ɜ ɜɟɪɧɨɫɬɢ ɩɪɢɜɟɞɟɧɧɨɣ ɮɨɪɦɭɥɵ.
Ɍɚɛɥɢɰɚ 2.8
x1 x0 |
ºx1ºx0 |
x1 x0 |
ºx1ºx0 x1 x0 |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
ɉɨɫɥɟɞɧɢɣ ɢɡ ɫɢɧɨɧɢɦɨɜ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɢ (ɟɫɥɢ x1, ɬɨ x0, ɂ ɟɫɥɢ x0, ɬɨ x1) ɩɨɡɜɨɥɹɟɬ ɫɨɫɬɚɜɢɬɶ ɞɥɹ ɧɟɟ ɟɳɟ ɢ ɬɚɤɨɟ ɜɵɪɚɠɟɧɢɟ:
(x1 x0) (x1ox0) (x0ox1).
ɑɢɬɚɬɟɥɸ ɩɪɟɞɥɚɝɚɟɬɫɹ ɩɪɨɜɟɪɢɬɶ ɜɟɪɧɨɫɬɶ ɷɬɨɣ ɮɨɪɦɭɥɵ ɫɚɦɨɫɬɨɹɬɟɥɶɧɨ.
23
ɉɨɥɟɡɧɨ ɛɵɜɚɟɬ ɩɪɨɢɡɜɟɫɬɢ ɚɧɚɥɢɡ ɩɪɚɜɨɜɵɯ ɧɨɪɦ ɫɪɟɞɫɬɜɚɦɢ ɚɥɝɟɛɪɵ ɥɨɝɢɤɢ ɞɥɹ ɨɛɧɚɪɭɠɟɧɢɹ ɢ ɭɫɬɪɚɧɟɧɢɹ ɜ ɧɢɯ ɧɟɹɫɧɨɫɬɟɣ, ɧɟɨɞɧɨɡɧɚɱɧɨɫɬɟɣ. ȼɨɡɶɦɟɦ, ɤ ɩɪɢɦɟɪɭ, ɬɚɤɨɟ ɜɵɫɤɚɡɵɜɚɧɢɟ:
«ɍɦɵɲɥɟɧɧɨɟ ɩɪɢɱɢɧɟɧɢɟ ɬɟɥɟɫɧɨɝɨ ɩɨɜɪɟɠɞɟɧɢɹ (x0) ɢɥɢ ɧɚɧɟɫɟɧɢɟ ɩɨɛɨɟɜ (x1), ɩɨɜɥɟɤɲɟɟ ɡɚ ɫɨɛɨɣ ɤɪɚɬɤɨɜɪɟɦɟɧɧɨɟ ɪɚɫɫɬɪɨɣɫɬɜɨ ɡɞɨɪɨɜɶɹ (x2) ɢɥɢ ɧɟɡɧɚɱɢɬɟɥɶɧɭɸ ɫɬɨɣɤɭɸ ɭɬɪɚɬɭ ɬɪɭɞɨɫɩɨɫɨɛɧɨɫɬɢ (x3), – ɧɚɤɚɡɵɜɚɟɬɫɹ ɥɢɲɟɧɢɟɦ ɫɜɨɛɨɞɵ ɧɚ ɫɪɨɤ ɞɨ ɨɞɧɨɝɨ ɝɨɞɚ (x4) ɢɥɢ ɢɫɩɪɚɜɢɬɟɥɶɧɵɦɢ ɪɚɛɨɬɚɦɢ ɧɚ ɬɨɬ ɠɟ ɫɪɨɤ (x5)».
ȼ ɬɟɤɫɬɟ ɷɬɨɝɨ ɭɬɜɟɪɠɞɟɧɢɹ ɤɚɠɞɨɟ ɩɪɨɫɬɨɟ ɜɵɫɤɚɡɵɜɚɧɢɟ ɦɵ ɨɛɨɡɧɚɱɢɥɢ ɫɜɨɟɣ ɥɨɝɢɱɟɫɤɨɣ ɩɟɪɟɦɟɧɧɨɣ. Ⱦɜɚ ɩɟɪɜɵɯ ɫɨɸɡɚ «ɢɥɢ» ɨɛɪɚɡɭɸɬ ɬɚɤɢɟ ɞɢɡɴɸɧɤɰɢɢ: x0 x1, x2 x3. Ⱥ ɜɨɬ ɬɪɟɬɢɣ ɫɨɸɡ «ɢɥɢ» ɫɥɟɞɨɜɚɥɨ ɛɵ ɡɚɦɟɧɢɬɶ ɪɚɡɞɟɥɢɬɟɥɶɧɵɦ ɫɨɸɡɨɦ «ɥɢɛɨ», ɩɨɫɤɨɥɶɤɭ ɨɞɧɨɜɪɟɦɟɧɧɨ ɞɜɚ ɧɚɤɚɡɚɧɢɹ ɧɚɡɧɚɱɟɧɵ ɛɵɬɶ ɧɟ ɦɨɝɭɬ. ɏɨɬɹ ɢ ɫɨɸɡ «ɢɥɢ» ɢɦɟɟɬ ɡɧɚɱɟɧɢɟ ɪɚɡɞɟɥɢɬɟɥɶɧɨɝɨ: «ɂɥɢ ɫɨ ɳɢɬɨɦ, ɢɥɢ ɧɚ ɳɢɬɟ!». (Ɉɬɦɟɬɢɦ ɩɨɩɭɬɧɨ, ɱɬɨ ɜ ɚɥɝɟɛɪɟ ɥɨɝɢɤɢ ɟɫɬɶ ɬɚɤɚɹ ɥɨɝɢɱɟɫɤɚɹ ɨɩɟɪɚɰɢɹ, ɤɚɤ ɢɫɤɥɸɱɚɸɳɟɟ ɂɅɂ. ȿɟ ɪɟɡɭɥɶɬɚɬ ɪɚɜɟɧ 1 ɬɨɥɶɤɨ ɬɨɝɞɚ, ɤɨɝɞɚ ɥɢɲɶ ɨɞɧɚ ɢɡ ɥɨɝɢɱɟɫɤɢɯ ɩɟɪɟɦɟɧɧɵɯ, ɧɚɞ ɤɨɬɨɪɵɦɢ ɜɵɩɨɥɧɹɟɬɫɹ ɷɬɚ ɨɩɟɪɚɰɢɹ, ɪɚɜɧɚ 1, ɚ ɜɫɟ ɨɫɬɚɥɶɧɵɟ ɢɦɟɸɬ ɡɧɚɱɟɧɢɟ 0.) Ⱦɚɥɟɟ, ɫɥɨɜɨ «ɩɨɜɥɟɤɲɟɟ» ɩɨ ɩɪɚɜɢɥɚɦ ɫɨɝɥɚɫɨɜɚɧɢɹ ɨɬɧɨɫɢɬɫɹ ɬɨɥɶɤɨ ɤ ɜɵɫɤɚɡɵɜɚɧɢɸ x1, ɚ ɩɨ ɫɦɵɫɥɭ ɨɧɨ ɨɬɧɨɫɢɬɫɹ ɤ ɨɛɨɢɦ ɩɪɟɫɬɭɩɧɵɦ ɞɟɣɫɬɜɢɹɦ x0 ɢ x1. ɇɟ ɭɥɭɱɲɚɟɬ ɫɢɬɭɚɰɢɸ ɢ ɦɧɨɠɟɫɬɜɟɧɧɨɟ ɱɢɫɥɨ «ɩɨɜɥɟɤɲɢɟ», ɩɨɫɤɨɥɶɤɭ x1 – «ɩɨɛɨɢ» ɬɨɠɟ ɫɬɨɢɬ ɜɨ ɦɧɨɠɟɫɬɜɟɧɧɨɦ ɱɢɫɥɟ. ȿɫɥɢ ɩɨɦɟɧɹɬɶ ɦɟɫɬɚɦɢ x0 ɢ x1, ɡɚɦɟɧɢɬɶ «ɩɨɜɥɟɤɲɟɟ» ɧɚ «ɩɨɜɥɟɤɲɢɟ», ɬɨ ɨɬɦɟɱɟɧɧɚɹ ɧɟɬɨɱɧɨɫɬɶ ɜ ɮɨɪɦɭɥɢɪɨɜɤɟ ɜɵɫɤɚɡɵɜɚɧɢɹ ɛɭɞɟɬ ɭɫɬɪɚɧɟɧɚ. Ɍɨɝɞɚ ɫɨɨɬɧɨɲɟɧɢɹ ɦɟɠɞɭ ɥɨɝɢɱɟɫɤɢɦɢ ɩɟɪɟɦɟɧɧɵɦɢ ɜ ɢɫɩɪɚɜɥɟɧɧɨɦ ɜɵɫɤɚɡɵɜɚɧɢɢ ɦɨɠɧɨ ɡɚɞɚɬɶ ɬɚɤɨɣ ɮɨɪɦɭɥɨɣ:
((x1 x0) (x2 x3))o((x4ºx5) (ºx4 x5)).
ɉɪɢɜɟɞɟɧɧɨɟ ɜɵɫɤɚɡɵɜɚɧɢɟ – ɫɭɬɶ ɫɬ. 112 ɭɬɪɚɬɢɜɲɟɝɨ ɫɢɥɭ ɍɄ ɊɋɎɋɊ. ȼ ɞɟɣɫɬɜɭɸɳɟɦ ɍɄ ɊɎ ɷɬɢɯ ɩɨɝɪɟɲɧɨɫɬɟɣ ɭɠɟ ɧɟɬ.
Ɉɬɦɟɬɢɦ, ɱɬɨ ɜ ɩɨɫɥɟɞɧɟɣ ɮɨɪɦɭɥɟ ɲɟɫɬɶ ɥɨɝɢɱɟɫɤɢɯ ɩɟɪɟɦɟɧɧɵɯ, ɢ ɩɨɫɬɪɨɢɬɶ ɞɥɹ ɧɟɟ ɬɚɛɥɢɰɭ ɢɫɬɢɧɧɨɫɬɢ ɧɟɩɪɨɫɬɨ. Ⱦɟɥɨ ɜ ɬɨɦ, ɱɬɨ ɬɚɛɥɢɰɚ ɢɫɬɢɧɧɨɫɬɢ ɞɥɹ n ɩɟɪɟɦɟɧɧɵɯ ɛɭɞɟɬ ɢɦɟɬɶ 2n ɫɬɪɨɤ ɞɥɹ ɜɫɟɯ ɤɨɦɛɢɧɚɰɢɣ (ɧɚɛɨɪɨɜ), ɫɨɫɬɚɜɥɹɸɳɢɯ ɡɧɚɱɟɧɢɹ ɷɬɢɯ ɩɟɪɟɦɟɧɧɵɯ (ɨɬ ɧɚɛɨɪɚ «ɜɫɟ – ɧɭɥɢ» ɞɨ ɧɚɛɨɪɚ «ɜɫɟ – ɟɞɢɧɢɰɵ»). ɉɪɢ n 6 ɜ ɬɚɛɥɢɰɟ ɛɭɞɟɬ 64 ɫɬɪɨɤɢ. ɉɪɢ ɟɟ ɡɚɩɨɥɧɟɧɢɢ ɧɭɠɧɨ ɧɟ ɩɪɨɩɭɫɬɢɬɶ ɧɢ ɨɞɧɨɝɨ ɢɡ ɧɚɛɨɪɨɜ, ɚ ɤɚɤɢɟ-ɬɨ ɢɡ ɧɚɛɨɪɨɜ – ɧɟ ɩɨɜɬɨɪɢɬɶ. ɉɪɚɜɞɚ, ɫɭɳɟɫɬɜɭɟɬ ɩɪɨɫɬɨɟ ɩɪɚɜɢɥɨ ɡɚɩɨɥɧɟɧɢɹ ɬɚɛɥɢɰɵ ɧɚɛɨɪɚɦɢ ɡɧɚɱɟɧɢɣ ɩɟɪɟɦɟɧɧɵɯ. Ɉɧɨ ɨɫɧɨɜɚɧɨ ɧɚ ɬɨɦ ɮɚɤɬɟ, ɱɬɨ ɥɸɛɚɹ ɢɡ ɥɨɝɢɱɟɫɤɢɯ ɩɟɪɟɦɟɧɧɵɯ ɧɚ ɩɨɥɨɜɢɧɟ ɢɡ 2n ɧɚɛɨɪɨɜ ɢɦɟɟɬ ɡɧɚɱɟɧɢɟ 0, ɚ ɧɚ ɞɪɭɝɨɣ ɩɨɥɨɜɢɧɟ – ɡɧɚɱɟɧɢɟ 1. Ɋɚɫɩɪɟɞɟɥɢɦ ɥɨɝɢɱɟɫɤɢɟ ɩɟɪɟɦɟɧɧɵɟ ɩɨ ɤɨ-
24
ɥɨɧɤɚɦ ɫɥɟɜɚ ɧɚɩɪɚɜɨ ɜ ɩɨɪɹɞɤɟ ɭɛɵɜɚɧɢɹ ɢɯ ɢɧɞɟɤɫɨɜ: x5 x4 x3 x2 x1 x0. ɉɪɚɜɭɸ ɤɨɥɨɧɤɭ ɞɥɹ x0 ɡɚɩɨɥɧɹɟɦ ɫɜɟɪɯɭ ɜɧɢɡ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɫɬɶɸ ɧɭɥɶ, ɨɞɢɧ, ɧɭɥɶ, ɨɞɢɧ ɢ ɬ.ɞ. ɞɨ ɩɨɫɥɟɞɧɟɣ ɫɬɪɨɤɢ ɬɚɛɥɢɰɵ. Ʉɨɥɨɧɤɭ ɞɥɹ x1 ɡɚɩɨɥɧɹɟɦ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɫɬɶɸ ɞɜɚ ɧɭɥɹ ɞɜɟ ɟɞɢɧɢɰɵ, ɤɨɥɨɧɤɭ ɞɥɹ x2 – ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɫɬɶ ɱɟɬɵɪɟ ɧɭɥɹ, ɱɟɬɵɪɟ ɟɞɢɧɢɰɵ. ɉɪɨɞɨɥɠɚɟɦ ɷɬɭ ɩɪɨɰɟɞɭɪɭ: ɱɚɫɬɨɬɚ ɫɦɟɧɵ ɧɭɥɟɣ ɢ ɟɞɢɧɢɰ ɜ ɤɚɠɞɨɣ ɫɥɟɞɭɸɳɟɣ ɤɨɥɨɧɤɟ ɜɞɜɨɟ ɦɟɧɶɲɟ, ɱɟɦ ɜ ɩɪɟɞɵɞɭɳɟɣ. ȼ ɫɚɦɨɣ ɥɟɜɨɣ ɤɨɥɨɧɤɟ ɞɥɹ x5 ɩɟɪɜɵɟ 32 ɫɬɪɨɤɢ ɛɭɞɭɬ ɡɚɩɨɥɧɟɧɵ ɧɭɥɹɦɢ, ɚ ɨɫɬɚɥɶɧɵɟ 32 ɫɬɪɨɤɢ – ɟɞɢɧɢɰɚɦɢ. ɂɦɟɧɧɨ ɩɨ ɷɬɨɦɭ ɩɪɚɜɢɥɭ ɦɵ ɡɚɩɨɥɧɹɥɢ ɬɚɛɥɢɰɵ ɢɫɬɢɧɧɨɫɬɢ ɞɨ ɫɢɯ ɩɨɪ ɢ ɛɭɞɟɦ ɢɯ ɡɚɩɨɥɧɹɬɶ ɜ ɩɨɫɥɟɞɭɸɳɟɦ.
2.2.Аксиомы и теоремы алгебры логики
ȼɛɭɥɟɜɨɣ ɚɥɝɟɛɪɟ ɞɥɹ ɥɸɛɵɯ ɜɵɫɤɚɡɵɜɚɧɢɣ A, B ɢ C ɫɩɪɚɜɟɞ-
ɥɢɜɵ ɫɥɟɞɭɸɳɢɟ ɚɤɫɢɨɦɵ 1..5 ɢ 1’..5’, ɚ ɬɚɤɠɟ ɢ ɬɟɨɪɟɦɵ 6..12 ɢ 6’..11’ (ɬɚɛɥ. 2.9). Ⱦɥɹ ɞɢɡɴɸɧɤɰɢɢ ɢ ɤɨɧɴɸɧɤɰɢɢ ɜ ɛɭɥɟɜɨɣ ɚɥɝɟɛɪɟ ɞɟɣɫɬɜɭɸɬ ɡɚɤɨɧɵ ɤɨɦɦɭɬɚɬɢɜɧɵɟ 1, 1’, ɚɫɫɨɰɢɚɬɢɜɧɵɟ 2, 2’ ɢ ɞɢɫɬɪɢɛɭɬɢɜɧɵɟ 3, 3’. Ʉɨɦɦɭɬɚɬɢɜɧɨɫɬɶ ɨɩɟɪɚɰɢɢ ɩɨɡɜɨɥɹɟɬ ɪɚɫɩɨɥɚɝɚɬɶ ɨɩɟɪɚɧɞɵ ɜ ɧɟɣ ɜ ɩɪɨɢɡɜɨɥɶɧɨɦ ɩɨɪɹɞɤɟ. Ⱥɫɫɨɰɢɚɬɢɜɧɨɫɬɶ ɩɨɡɜɨɥɹɟɬ ɫɜɟɫɬɢ ɦɧɨɝɨɦɟɫɬɧɭɸ ɨɩɟɪɚɰɢɸ ɤ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɫɬɢ ɞɜɭɦɟɫɬɧɵɯ. Ⱦɢɫɬɪɢɛɭɬɢɜɧɨɫɬɶ ɩɨɡɜɨɥɹɟɬ ɜɵɧɨɫɢɬɶ ɡɚ ɫɤɨɛɤɢ ɨɞɧɨɪɨɞɧɵɟ ɱɥɟɧɵ ɢɥɢ ɡɚɞɚɟɬ ɩɪɚɜɢɥɨ ɪɚɫɤɪɵɬɢɹ ɫɤɨɛɨɤ.
Ʉɚɤ ɜɢɞɢɦ, ɩɪɢɜɟɞɟɧɧɚɹ ɫɢɫɬɟɦɚ ɚɤɫɢɨɦ ɢ ɬɟɨɪɟɦ ɚɥɝɟɛɪɵ ɥɨɝɢɤɢ ɨɬɜɟɱɚɟɬ ɩɪɢɧɰɢɩɭ ɞɜɨɣɫɬɜɟɧɧɨɫɬɢ.
Ɍɚɛɥɢɰɵ, ɤɨɬɨɪɵɟ ɡɚɞɚɸɬ ɨɩɟɪɚɰɢɢ ɚɥɝɟɛɪɵ ɥɨɝɢɤɢ, ɬɨɠɟ ɩɨ ɫɭɬɢ ɫɜɨɟɣ ɚɤɫɢɨɦɵ. Ɂɚɦɟɧɢɦ ɜ ɷɬɢɯ ɬɚɛɥɢɰɚɯ ɥɨɝɢɱɟɫɤɢɟ ɩɟɪɟɦɟɧɧɵɟ ɩɪɨ-
ɢɡɜɨɥɶɧɵɦɢ ɜɵɫɤɚɡɵɜɚɧɢɹɦɢ A ɢ B ɢ ɫɜɟɞɟɦ ɢɯ ɜ ɨɞɧɭ ɨɛɳɭɸ ɬɚɛɥ.2.10. ɉɪɢɨɪɢɬɟɬɵ ɷɬɢɯ ɨɩɟɪɚɰɢɣ ɭɛɵɜɚɸɬ ɜ ɬɚɤɨɦ ɩɨɪɹɞɤɟ: ɨɬɪɢɰɚɧɢɟ, ɤɨɧɴɸɧɤɰɢɹ, ɞɢɡɴɸɧɤɰɢɹ, ɢɦɩɥɢɤɚɰɢɹ, ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɶ.
ɇɚɤɨɧɟɰ, ɩɪɢɜɟɞɟɦ ɮɨɪɦɭɥɵ (2.1) ɢ (2.2), ɤɨɬɨɪɵɟ ɩɨɡɜɨɥɹɸɬ ɩɪɟɞɫɬɚɜɢɬɶ ɢɦɩɥɢɤɚɰɢɸ ɢ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɶ ɞɥɹ ɜɵɫɤɚɡɵɜɚɧɢɣ A ɢ B ɜ ɬɟɪɦɢɧɚɯ ɮɭɧɤɰɢɨɧɚɥɶɧɨ ɩɨɥɧɨɣ ɫɢɫɬɟɦɵ ɨɩɟɪɚɰɢɣ ɚɥɝɟɛɪɵ ɥɨɝɢɤɢ.
|
Ɍɚɛɥɢɰɚ 2.11 |
Ʉɚɠɞɚɹ ɢɡ ɬɟɨɪɟɦ ɥɟɝɤɨ ɞɨɤɚɡɵɜɚɟɬɫɹ ɫ |
|||
|
ɩɨɦɨɳɶɸ ɬɚɛɥ.2.9 ɢ ɬɚɛɥ. 2.10. Ɍɚɤ, ɭɬɜɟɪ- |
||||
A |
B ºA |
C ºB ººA |
ɠɞɟɧɢɟ 12, ɤɨɬɨɪɨɟ ɧɚɡɵɜɚɟɬɫɹ ɡɚɤɨɧɨɦ |
||
|
|
|
ɞɜɨɣɧɨɝɨ ɨɬɪɢɰɚɧɢɹ, |
ɞɨɤɚɡɵɜɚɟɬɫɹ |
|
0 |
1 |
0 |
|||
ɧɟɩɨɫɪɟɞɫɬɜɟɧɧɨɣ ɩɪɨɜɟɪɤɨɣ |
(ɬɚɛɥ.2.11). |
||||
1 |
0 |
1 |
|||
ɇɚɩɪɢɦɟɪ, ɜɵɫɤɚɡɵɜɚɧɢɟ |
|
||||
«ɇɟɩɪɚɜɞɚ, ɱɬɨ ɦɚɬɟɦɚɬɢɤɚ ɸɪɢɫɬɭ ɧɟ ɧɭɠɧɚ» — ɧɟ ɱɬɨ ɢɧɨɟ, ɤɚɤ ɞɜɨɣɧɨɟ ɨɬɪɢɰɚɧɢɟ ɢɫɯɨɞɧɨɝɨ ɭɬɜɟɪɠɞɟɧɢɹ
«Ɇɚɬɟɦɚɬɢɤɚ ɸɪɢɫɬɭ ɧɭɠɧɚ».
25

ɍɬɜɟɪɠɞɟɧɢɹ 9 ɢ 9’ ɧɚɡɵɜɚɸɬɫɹ ɡɚɤɨɧɚɦɢ ɫɤɥɟɢɜɚɧɢɹ. Ⱦɨɤɚɠɟɦ ɜɬɨɪɨɟ ɢɡ ɷɬɢɯ ɭɬɜɟɪɠɞɟɧɢɣ:
(A B) (AºB) ¢3² A (BºB) ¢5’² A 0 ¢4² A.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍɚɛɥɢɰɚ 2.9 |
|
1 |
|
|
A B B A |
|
|
|
5 |
|
AºA 1 |
|
|
9 |
(A B) (AºB) A |
||||
|
1’ |
|
A B B A |
|
|
|
|
5’ |
AºA 0 |
|
|
9’ |
(A B) (AºB) A |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
A B C (A B) C |
|
|
6 |
|
A 1 1 |
|
|
10 |
º(A B) ºAºB |
|||||
|
2’ |
|
A B C (A B) C |
|
|
|
6’ |
A 0 0 |
|
|
10’ |
º(A B) ºAºB |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
A (B C) (A B) (A C) |
|
7 |
|
A A A |
|
|
11 |
º0 1 |
|
|||||
|
3’ |
|
A (B C) (A B) (A C) |
|
|
7’ |
A A A |
|
|
11’ |
º1 0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4 |
|
|
A 0 A |
|
|
|
|
8 |
|
A (A B) A |
|
12 |
ººA A |
|
|||
|
4’ |
|
A 1 A |
|
|
|
|
|
8’ |
A (A B) A |
|
|
|
|
|||
|
|
|
|
|
|
|
Ɍɚɛɥɢɰɚ 2.10 |
|
|
|
|
|
|||||
A B |
ºA |
A B |
A B |
AoB |
(A B) |
|
|
|
|
|
|
||||||
0 |
0 |
|
1 |
|
0 |
0 |
1 |
|
|
1 |
|
|
AoB ºA B |
|
(2.1) |
||
0 |
1 |
|
1 |
|
0 |
1 |
1 |
|
|
0 |
|
|
(A B) ºAºB A B |
(2.2) |
|||
1 |
0 |
|
0 |
|
0 |
1 |
0 |
|
|
0 |
|
|
|
|
|
|
|
1 |
1 |
|
0 |
|
1 |
1 |
1 |
|
|
1 |
|
|
|
|
|
|
|
ɑɢɬɚɬɟɥɸ ɩɪɟɞɥɨɠɢɦ ɫɚɦɨɫɬɨɹɬɟɥɶɧɨ ɞɨɤɚɡɚɬɶ ɭɬɜɟɪɠɞɟɧɢɹ 10 ɢ 10’, ɤɨɬɨɪɵɟ ɧɚɡɵɜɚɸɬɫɹ ɩɪɚɜɢɥɚɦɢ ɞɟ Ɇɨɪɝɚɧɚ (ɩɨ ɢɦɟɧɢ ɲɨɬɥɚɧɞɫɤɨɝɨ ɦɚɬɟɦɚɬɢɤɚ ɢ ɥɨɝɢɤɚ Ɉɝɸɫɬɚ ɞɟ Ɇɨɪɝɚɧɚ, ɩɟɪɜɨɝɨ ɩɪɟɡɢɞɟɧɬɚ Ʌɨɧɞɨɧɫɤɨɝɨ ɦɚɬɟɦɚɬɢɱɟɫɤɨɝɨ ɨɛɳɟɫɬɜɚ). Ɇɵ ɠɟ ɩɪɨɢɥɥɸɫɬɪɢɪɭɟɦ ɨɞɧɨ ɢɡ ɷɬɢɯ ɩɪɚɜɢɥ ɬɚɤɢɦ ɩɪɢɦɟɪɨɦ. ɉɪɨ ɤɨɝɨ-ɬɨ ɝɨɜɨɪɹɬ: «ɇɢ ɪɵɛɚ, ɧɢ ɦɹɫɨ!». ɋɪɟɞɫɬɜɚɦɢ ɥɨɝɢɤɢ ɷɬɚ ɮɪɚɡɚ ɫɬɪɨɢɬɫɹ ɬɚɤ: (ɨɧ ɇȿ ɪɵɛɚ) ɂ (ɨɧ ɇȿ ɦɹɫɨ). Ʌɟɝɤɨ ɜɢɞɟɬɶ, ɱɬɨ ɷɬɨ ɩɪɚɜɚɹ ɱɚɫɬɶ ɬɨɠɞɟɫɬɜɚ 10. Ɍɭ ɠɟ ɦɵɫɥɶ ɦɨɠɧɨ ɫɮɨɪɦɭɥɢɪɨɜɚɬɶ ɢɧɚɱɟ: ɇȿɉɊȺȼȾȺ, ɱɬɨ (ɨɧ ɪɵɛɚ ɂɅɂ ɨɧ ɦɹɫɨ). Ⱥ ɷɬɚ ɤɨɧɫɬɪɭɤɰɢɹ – ɥɟɜɚɹ ɱɚɫɬɶ ɬɨɠɞɟɫɬɜɚ 10.
ɉɪɢɜɟɞɟɧɧɵɟ ɬɨɠɞɟɫɬɜɚ 1..11, 1’..11’ ɢ 12 ɦɨɠɧɨ ɢɫɩɨɥɶɡɨɜɚɬɶ ɞɥɹ ɷɤɜɢɜɚɥɟɧɬɧɵɯ ɩɪɟɨɛɪɚɡɨɜɚɧɢɣ ɚɧɚɥɢɬɢɱɟɫɤɢɯ ɜɵɪɚɠɟɧɢɣ ɢ ɞɥɹ ɞɨɤɚɡɚɬɟɥɶɫɬɜɚ ɥɸɛɵɯ ɞɪɭɝɢɯ ɭɬɜɟɪɠɞɟɧɢɣ ɚɥɝɟɛɪɵ ɥɨɝɢɤɢ.
26
Ɉɞɧɚɤɨ ɜ ɬɚɛɥ.2.9 ɧɟɬ ɨɩɟɪɚɰɢɣ ɢɦɩɥɢɤɚɰɢɢ ɢ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɢ. ɉɨɷɬɨɦɭ ɩɪɟɠɞɟ ɱɟɦ ɜɨɫɩɨɥɶɡɨɜɚɬɶɫɹ ɷɬɢɦɢ ɬɨɠɞɟɫɬɜɚɦɢ, ɜ ɢɫɯɨɞɧɨɦ ɜɵɪɚɠɟɧɢɢ ɧɟɨɛɯɨɞɢɦɨ ɫ ɩɨɦɨɳɶɸ ɮɨɪɦɭɥ (2.1) ɢ (2.2) ɜɵɪɚɡɢɬɶ ɢɦɩɥɢɤɚɰɢɢ ɢ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɢ ɜ ɬɟɪɦɢɧɚɯ ɮɭɧɤɰɢɨɧɚɥɶɧɨ ɩɨɥɧɨɣ ɫɢɫɬɟɦɵ ɨɩɟɪɚɰɢɣ.
Ɋɚɫɫɦɨɬɪɢɦ ɬɚɤɨɣ ɩɪɢɦɟɪ. ɀɸɪɢ ɢɡ ɬɪɟɯ ɱɟɥɨɜɟɤ A, B, C ɩɪɢɧɢɦɚɟɬ ɪɟɲɟɧɢɟ ɛɨɥɶɲɢɧɫɬɜɨɦ ɝɨɥɨɫɨɜ. ɉɪɢ ɷɬɨɦ ɤɚɠɞɵɣ ɱɥɟɧ ɠɸɪɢ ɦɨɠɟɬ ɝɨɥɨɫɨɜɚɬɶ ɥɢɛɨ «ɡɚ», ɥɢɛɨ «ɩɪɨɬɢɜ». Ɉɩɢɲɟɦ ɫɪɟɞɫɬɜɚɦɢ ɚɥɝɟɛɪɵ ɥɨɝɢɤɢ ɜɫɟ ɜɨɡɦɨɠɧɵɟ ɪɟɡɭɥɶɬɚɬɵ ɝɨɥɨɫɨɜɚɧɢɹ. Ⱦɥɹ ɷɬɨɝɨ ɤɚɠɞɨɦɭ ɢɡ ɱɥɟɧɨɜ ɠɸɪɢ ɩɨɫɬɚɜɢɦ ɜ ɫɨɨɬɜɟɬɫɬɜɢɟ ɫɜɨɸ ɥɨɝɢɱɟɫɤɭɸ ɩɟɪɟɦɟɧɧɭɸ D (D {A,B,C}), ɤɨɬɨɪɚɹ ɩɪɢɧɢɦɚɟɬ ɡɧɚɱɟɧɢɟ 0, ɟɫɥɢ ɨɧ ɝɨɥɨɫɭɟɬ «ɩɪɨɬɢɜ», ɢ ɡɧɚɱɟɧɢɟ 1, ɤɨɝɞɚ ɨɧ ɝɨɥɨɫɭɟɬ «ɡɚ». Ʌɨɝɢɱɟɫɤɚɹ ɩɟɪɟɦɟɧɧɚɹ R ɩɪɢɧɢɦɚɟɬ ɡɧɚɱɟɧɢɟ 0, ɟɫɥɢ ɪɟɲɟɧɢɟ ɧɟ ɩɪɢɧɢɦɚɟɬɫɹ, ɢ ɡɧɚɱɟɧɢɟ 1, ɟɫɥɢ ɨɧɨ ɩɪɢɧɢɦɚɟɬɫɹ.
Ⱥɬɟɩɟɪɶ ɫɨɫɬɚɜɢɦ ɬɚɛɥɢɰɭ ɢɫɬɢɧɧɨɫɬɢ
(ɬɚɛɥ.2.12). Ʉɨɥɨɧɤɢ ɞɥɹ C, B ɢ A ɡɚɩɨɥɧɹɟɦ ɩɨ
ɨɩɢɫɚɧɧɨɦɭ ɜɵɲɟ ɩɪɚɜɢɥɭ. Ʉɚɤ ɜɢɞɢɦ, R ɪɚɜɧɨ 1 ɬɨɝɞɚ, ɤɨɝɞɚ ɯɨɬɹ ɛɵ ɞɜɚ ɢɡ ɬɪɟɯ ɚɪɝɭɦɟɧɬɨɜ A, B ɢ C ɪɚɜɧɵ 1 (ɯɨɬɹ ɛɵ ɞɜɚ ɢɡ ɬɪɟɯ ɱɥɟɧɨɜ ɠɸɪɢ ɝɨɥɨɫɭɸɬ «ɡɚ»). ɉɨ ɞɚɧɧɵɦ ɬɚɛɥɢɰɵ ɢɫɬɢɧɧɨɫɬɢ ɦɨɠɧɨ ɩɨɫɬɪɨɢɬɶ ɚɧɚɥɢɬɢɱɟɫɤɨɟ ɜɵɪɚɠɟɧɢɟ ɞɥɹ R. Ɋɚɫɫɦɨɬɪɢɦ ɨɞɢɧ ɢɡ ɜɨɡɦɨɠɧɵɯ ɫɩɨɫɨɛɨɜ ɩɨɥɭɱɢɬɶ ɢɡ ɬɚɛɥɢɰɵ ɢɫɬɢɧɧɨɫɬɢ ɚɧɚɥɢɬɢɱɟɫɤɨɟ ɜɵɪɚɠɟɧɢɟ
ɞɥɹ R, ɚ ɢɦɟɧɧɨ, «ɩɨɫɬɪɨɟɧɢɟ ɮɨɪɦɭɥɵ ɩɨ ɟɞɢɧɢɰɚɦ». Ⱦɥɹ ɷɬɨɝɨ ɜɵɞɟɥɢɦ ɜ ɬɚɛɥ.2.11 ɬɟ
ɫɬɪɨɤɢ, ɜ ɤɨɬɨɪɵɯ R 1, ɢ ɫɨɫɬɚɜɢɦ ɞɥɹ ɤɚɠɞɨɣ ɢɡ ɷɬɢɯ ɫɬɪɨɤ ɤɨɧɴɸɧɤɰɢɸ ɜɫɟɯ ɚɪɝɭɦɟɧɬɨɜ. ɉɪɢ
A |
B |
C |
R |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
ɷɬɨɦ ɩɟɪɟɦɟɧɧɚɹ D (D {A,B,C}) ɜɯɨɞɢɬ ɜ ɬɚɤɭɸ
ɤɨɧɴɸɧɤɰɢɸ ɩɪɹɦɨ, ɟɫɥɢ ɜ ɞɚɧɧɨɣ ɫɬɪɨɤɟ D 1, ɟɫɥɢ ɠɟ ɡɞɟɫɶ D 0, ɬɨ ɨɧɚ ɜɯɨɞɢɬ ɜ ɤɨɧɴɸɧɤɰɢɸ ɩɨɞ ɡɧɚɤɨɦ ɢɧɜɟɪɫɢɢ. ɉɨɥɭɱɟɧɧɵɟ ɤɨɧɴɸɧɤɰɢɢ ɨɛɴɟɞɢɧɢɦ ɨɩɟɪɚɰɢɟɣ ɞɢɡɴɸɧɤɰɢɢ. Ɍɨɝɞɚ:
R (ºA B C) (AºB C) (A BºC) (A B C).
ɉɨɥɶɡɭɹɫɶ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɹɦɢ ɚɥɝɟɛɪɵ ɥɨɝɢɤɢ, ɷɬɨ ɜɵɪɚɠɟɧɢɟ ɦɨɠɧɨ ɭɩɪɨɫɬɢɬɶ:
R ¢7² (ºA B C) (AºB C) (A BºC)
(A B C) (A B C) (A B C) ¢2²
(ºA B C A B C) (AºB C A B C) (A BºC A B C)
¢9, 6’² B C A C A B.
27
ɉɪɢɜɟɞɟɧɧɵɟ ɪɚɧɟɟ ɜɵɪɚɠɟɧɢɹ ɞɥɹ ɢɦɩɥɢɤɚɰɢɢ ɢ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɢ ɜ ɬɟɪɦɢɧɚɯ ɛɭɥɟɜɨɣ ɚɥɝɟɛɪɵ ɛɵɥɢ ɩɨɥɭɱɟɧɵ ɢɦɟɧɧɨ ɬɚɤɢɦ ɫɩɨɫɨɛɨɦ (ɩɨɫɬɪɨɟɧɵ ɩɨ ɟɞɢɧɢɰɚɦ).
ȿɳɟ ɨɞɢɧ ɩɪɢɦɟɪ, ɤɨɬɨɪɵɣ ɧɚɡɵɜɚɸɬ ɡɚɤɨɧɨɦ ɞɨɫɬɚɬɨɱɧɨɝɨ ɨɫɧɨɜɚɧɢɹ. ɘɪɢɞɢɱɟɫɤɚɹ ɢɧɬɟɪɩɪɟɬɚɰɢɹ ɷɬɨɝɨ ɡɚɤɨɧɚ ɦɨɠɟɬ ɛɵɬɶ ɬɚɤɨɣ: ɟɫɥɢ ɫɨɫɬɚɜɥɟɧ ɩɟɪɟɱɟɧɶ ɭɥɢɤ (A), ɞɨɫɬɚɬɨɱɧɵɣ ɞɥɹ ɡɚɤɥɸɱɟɧɢɹ ɨ ɜɢɧɨɜɧɨɫɬɢ (B), ɢ ɷɬɢ ɭɥɢɤɢ ɫɨɛɪɚɧɵ (Ⱥ), ɬɨ ɨɛɜɢɧɹɟɦɵɣ ɜɢɧɨɜɟɧ (ȼ).
ɇɚ ɹɡɵɤɟ ɚɥɝɟɛɪɵ ɜɵɫɤɚɡɵɜɚɧɢɣ ɷɬɨɬ ɡɚɤɨɧ ɦɨɠɧɨ ɜɵɪɚɡɢɬɶ ɬɚɤɨɣ ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɶɸ:
(((AoB) A)oB) 1.
ɉɨɤɚɠɟɦ, ɱɬɨ ɨɛɳɚɹ ɫɯɟɦɚ ɪɚɫɫɭɠɞɟɧɢɣ ɜ ɮɨɪɦɭɥɢɪɨɜɤɟ ɡɚɤɨɧɚ ɜɟɪɧɚ (ɚɪɝɭɦɟɧɬɚɰɢɹ ɨɛɜɢɧɟɧɢɹ ɥɨɝɢɱɟɫɤɢ ɤɨɪɪɟɤɬɧɚ). ɋɧɚɱɚɥɚ ɭɩɪɨɫɬɢɦ ɩɨɫɵɥɤɭ ɜɬɨɪɨɣ ɢɦɩɥɢɤɚɰɢɢ:
(AoB) A ¢(2.1)² (ºA B) A ¢3’² (ºA A) (B A) ¢5’² 0 B A ¢4,1² A B.
ɋɥɟɞɨɜɚɬɟɥɶɧɨ,
(((AoB) A)oB) ((A B)oB) ¢(2.1)² (º(A B) B) ¢10’² ºA
ºB B ¢5,6² 1.
Ɂɧɚɱɢɬ, ɥɨɝɢɱɟɫɤɢ ɮɨɪɦɭɥɢɪɨɜɤɚ ɡɚɤɨɧɚ ɞɨɫɬɚɬɨɱɧɨɝɨ ɨɫɧɨɜɚɧɢɹ ɜɟɪɧɚ.
ɂɬɚɤ, ɦɚɬɟɦɚɬɢɱɟɫɤɚɹ ɥɨɝɢɤɚ ɪɚɡɜɢɜɚɟɬ ɤɭɥɶɬɭɪɭ ɥɨɝɢɱɧɵɯ ɪɚɫɫɭɠɞɟɧɢɣ, ɧɟɨɛɯɨɞɢɦɭɸ ɜ ɥɸɛɨɣ ɨɛɥɚɫɬɢ ɡɧɚɧɢɣ (ɚ ɜ ɸɪɢɫɩɪɭɞɟɧɰɢɢ – ɨɫɨɛɟɧɧɨ). Ɉɞɧɚɤɨ ɧɭɠɧɨ ɡɚɦɟɬɢɬɶ, ɱɬɨ ɩɪɢɦɟɧɢɦɨɫɬɶ ɫɪɟɞɫɬɜ ɚɥɝɟɛɪɵ ɥɨɝɢɤɢ ɨɝɪɚɧɢɱɟɧɚ. Ɍɚɤ, ɭɬɜɟɪɠɞɟɧɢɹ A B ɢ B A ɜ ɚɥɝɟɛɪɟ ɥɨɝɢɤɢ ɚɛɫɨɥɸɬɧɨ ɨɞɢɧɚɤɨɜɵ ɜ ɫɢɥɭ ɚɤɫɢɨɦɵ 1’. Ⱥ ɜɨɬ ɮɪɚɡɵ «ɍ Ⱦɠɟɣɧ ɪɨɞɢɥɫɹ ɪɟɛɟɧɨɤ (A), ɢ ɨɧɚ ɜɵɲɥɚ ɡɚɦɭɠ (B)» ɢ «Ⱦɠɟɣɧ ɜɵɲɥɚ ɡɚɦɭɠ (B), ɢ ɭ ɧɟɟ ɪɨɞɢɥɫɹ ɪɟɛɟɧɨɤ (A)» ɩɨɧɢɦɚɸɬɫɹ ɩɨ-ɪɚɡɧɨɦɭ. ɗɬɨ ɨɛɭɫɥɨɜɥɟɧɨ ɬɟɦ, ɱɬɨ ɷɥɟɦɟɧɬɚɪɧɵɟ ɜɵɫɤɚɡɵɜɚɧɢɹ ɜ ɩɪɢɜɟɞɟɧɧɵɯ ɮɪɚɡɚɯ ɫɥɟɞɭɸɬ ɨɞɧɨ ɡɚ ɞɪɭɝɢɦ ɜɨ ɜɪɟɦɟɧɢ.
Ⱥ ɜ ɚɥɝɟɛɪɟ ɜɵɫɤɚɡɵɜɚɧɢɣ ɜɪɟɦɹ ɧɟ ɹɜɥɹɟɬɫɹ ɚɪɝɭɦɟɧɬɨɦ – ɷɥɟɦɟɧɬɚɪɧɵɟ ɜɵɫɤɚɡɵɜɚɧɢɹ ɧɟ ɪɚɫɩɪɟɞɟɥɹɸɬɫɹ ɜɨ ɜɪɟɦɟɧɢ. Ɂɧɚɱɢɬ, ɫɬɪɟɦɢɬɶɫɹ ɩɟɪɟɜɟɫɬɢ ɪɚɫɫɭɠɞɟɧɢɹ ɧɚ ɹɡɵɤ ɚɥɝɟɛɪɵ ɥɨɝɢɤɢ ɢ ɚɧɚɥɢɡɢɪɨɜɚɬɶ ɷɬɢ ɪɚɫɫɭɠɞɟɧɢɹ ɟɟ ɫɪɟɞɫɬɜɚɦɢ ɧɭɠɧɨ, ɨɞɧɚɤɨ ɩɪɢ ɷɬɨɦ ɫɥɟɞɭɟɬ ɛɵɬɶ ɚɤɤɭɪɚɬɧɵɦ. Ʉ ɬɨɦɭ ɠɟ ɟɫɬɶ ɫɥɭɱɚɢ, ɤɨɝɞɚ ɷɬɨ ɢ ɜɨɜɫɟ ɧɟɜɨɡɦɨɠɧɨ ɫɞɟɥɚɬɶ. ɇɚɩɪɢɦɟɪ, ɭɬɜɟɪɠɞɟɧɢɟ A ºA 0 ɚɛɫɨɥɸɬɧɨ ɜɟɪɧɨ. Ⱥ ɜɨɬ ɫɬɪɨɤɢ ɢɡ ɫɬɢɯɨɬɜɨɪɟɧɢɹ ɫɪɟɞɧɟɜɟɤɨɜɨɣ ɮɪɚɧɰɭɡɫɤɨɣ ɩɨɷɬɟɫɫɵ Ʌ. Ʌɚɛɟ:
Ɉɬ ɫɱɚɫɬɶɹ ɹ ɜ ɬɨɫɤɟ ɫɦɟɪɬɟɥɶɧɨɣ ɩɥɚɱɭ, Ʌɟɝɤɚ ɦɧɟ ɠɢɡɧɶ, ɥɟɝɤɚ ɢ ɬɹɠɟɥɚ.
28
ɧɟɩɨɞɜɥɚɫɬɧɵ ɷɬɨɦɭ ɡɚɤɨɧɭ. ɗɬɨ ɡɧɚɱɢɬ, ɱɬɨ ɨɬɧɸɞɶ ɧɟ ɜɫɹɤɭɸ ɝɚɪɦɨɧɢɸ ɦɨɠɧɨ ɩɪɨɜɟɪɢɬɶ ɚɥɝɟɛɪɨɣ (ɩɭɫɬɶ ɷɬɨ ɞɚɠɟ ɢ ɚɥɝɟɛɪɚ ɥɨɝɢɤɢ).
Вопросы и задачи для самоконтроля
1.Ɉɩɪɟɞɟɥɢɬɶ ɨɫɧɨɜɧɵɟ ɩɨɧɹɬɢɹ ɦɚɬɟɦɚɬɢɱɟɫɤɨɣ ɥɨɝɢɤɢ: «ɜɵɫɤɚɡɵɜɚɧɢɟ», «ɩɪɨɫɬɨɟ ɜɵɫɤɚɡɵɜɚɧɢɟ», «ɫɥɨɠɧɨɟ ɜɵɫɤɚɡɵɜɚɧɢɟ».
2.ɉɪɢɜɟɫɬɢ ɨɩɪɟɞɟɥɟɧɢɹ ɥɨɝɢɱɟɫɤɢɯ ɨɩɟɪɚɰɢɣ: ɨɬɪɢɰɚɧɢɟ, ɤɨɧɴɸɧɤɰɢɹ, ɞɢɡɴɸɧɤɰɢɹ, ɢɦɩɥɢɤɚɰɢɹ, ɷɤɜɢɜɚɥɟɧɬɧɨɫɬɶ.
3.ɉɟɪɟɜɟɫɬɢ ɧɚ ɹɡɵɤ ɚɥɝɟɛɪɵ ɥɨɝɢɤɢ ɫɥɟɞɭɸɳɢɟ ɩɪɟɞɥɨɠɟɧɢɹ:
ɚ) ɍɝɨɥɨɜɧɨɣ ɨɬɜɟɬɫɬɜɟɧɧɨɫɬɢ ɩɨɞɥɟɠɢɬ ɥɢɰɨ, ɞɨɫɬɢɝɲɟɟ ɤɨ ɜɪɟɦɟɧɢ ɫɨɜɟɪɲɟɧɢɹ ɩɪɟɫɬɭɩɥɟɧɢɹ ɲɟɫɬɧɚɞɰɚɬɢɥɟɬɧɟɝɨ ɜɨɡɪɚɫɬɚ.
ɛ) Ʌɢɰɨ ɧɟ ɩɨɞɥɟɠɢɬ ɭɝɨɥɨɜɧɨɣ ɨɬɜɟɬɫɬɜɟɧɧɨɫɬɢ ɡɚ ɩɪɟɫɬɭɩɥɟɧɢɟ, ɟɫɥɢ ɨɧɨ ɞɨɛɪɨɜɨɥɶɧɨ ɢ ɨɤɨɧɱɚɬɟɥɶɧɨ ɨɬɤɚɡɚɥɨɫɶ ɨɬ ɞɨɜɟɞɟɧɢɹ ɷɬɨɝɨ ɩɪɟɫɬɭɩɥɟɧɢɹ ɞɨ ɤɨɧɰɚ.
ɜ) Ⱦɟɡɟɪɬɢɪɫɬɜɨ ɫ ɨɪɭɠɢɟɦ, ɜɜɟɪɟɧɧɵɦ ɩɨ ɫɥɭɠɛɟ, ɚ ɪɚɜɧɨ ɞɟɡɟɪɬɢɪɫɬɜɨ, ɫɨɜɟɪɲɟɧɧɨɟ ɝɪɭɩɩɨɣ ɥɢɰ ɩɨ ɩɪɟɞɜɚɪɢɬɟɥɶɧɨɦɭ ɫɝɨɜɨɪɭ ɢɥɢ ɨɪɝɚɧɢɡɨɜɚɧɧɨɣ ɝɪɭɩɩɨɣ, ɧɚɤɚɡɵɜɚɟɬɫɹ ɥɢɲɟɧɢɟɦ ɫɜɨɛɨɞɵ ɧɚ ɫɪɨɤ ɨɬ ɬɪɟɯ ɞɨ ɞɟɫɹɬɢ ɥɟɬ.
ɝ) x y ɢɥɢ x y;
ɞ) ɟɫɥɢ x!y, ɚ y!z, ɬɨ v w;
4.ɋɨɫɬɚɜɢɬɶɬɚɛɥɢɰɵ ɢɫɬɢɧɧɨɫɬɢ ɞɥɹ ɫɥɟɞɭɸɳɢɯ ɜɵɫɤɚɡɵɜɚɧɢɣ:
ɚ) Po(PoQ); ɛ) Poº(Q R); ɜ) (Po(Q R)) (ºP Q).
5.Ⱦɨɤɚɡɚɬɶ ɢɫɬɢɧɧɨɫɬɶ ɫɥɟɞɭɸɳɢɯ ɭɬɜɟɪɠɞɟɧɢɣ:
ɚ) º(A ºA) 1 – ɡɚɤɨɧ ɩɪɨɬɢɜɨɪɟɱɢɹ,
ɛ) A (AoB)oB – ɩɪɚɜɢɥɨ ɢɡɜɥɟɱɟɧɢɹ ɫɥɟɞɫɬɜɢɹ, ɜ) (AoºA)oºA – ɩɪɢɧɰɢɩ ɩɪɢɜɟɞɟɧɢɹ ɤ ɚɛɫɭɪɞɭ, ɝ) (AoB) (ºBoºA) – ɡɚɤɨɧ ɤɨɧɬɪɚɩɨɡɢɰɢɢ,
ɞ) ((AoB) (BoC))o(AoC) – ɡɚɤɨɧ ɫɢɥɥɨɝɢɡɦɚ.
29
РАЗДЕЛ II.
Основы математического анализа
ȼɪɟɦɹ ɫɨɞɟɪɠɚɧɢɹ ɥɢɰɚ ɩɨɞ ɫɬɪɚɠɟɣ ɞɨ ɫɭɞɟɛɧɨɝɨ ɪɚɡɛɢɪɚɬɟɥɶɫɬɜɚ ɡɚɫɱɢɬɵɜɚɟɬɫɹ ɜ ɫɪɨɤɢ ɥɢɲɟɧɢɹ ɫɜɨɛɨɞɵ, ɫɨɞɟɪɠɚɧɢɹ ɜ ɞɢɫɰɢɩɥɢɧɚɪɧɨɣ ɜɨɢɧɫɤɨɣ ɱɚɫɬɢ ɢ ɚɪɟɫɬɚ ɢɡ ɪɚɫɱɟɬɚ ɨɞɢɧ ɞɟɧɶ ɡɚ ɨɞɢɧ ɞɟɧɶ, ɨɝɪɚɧɢɱɟɧɢɹ ɫɜɨɛɨɞɵ – ɨɞɢɧ ɞɟɧɶ ɡɚ ɞɜɚ ɞɧɹ, ɢɫɩɪɚɜɢɬɟɥɶɧɵɯ ɪɚɛɨɬ ɢ ɨɝɪɚɧɢɱɟɧɢɹ ɩɨ ɜɨɟɧɧɨɣ ɫɥɭɠɛɟ – ɨɞɢɧ ɞɟɧɶ ɡɚ ɬɪɢ ɞɧɹ, ɚ ɜ ɫɪɨɤ ɨɛɹɡɚɬɟɥɶɧɵɯ ɪɚɛɨɬ – ɢɡ ɪɚɫɱɟɬɚ ɨɞɢɧ ɞɟɧɶ ɫɨɞɟɪɠɚɧɢɹ ɩɨɞ
ɫɬɪɚɠɟɣ ɡɚ ɜɨɫɟɦɶ ɱɚɫɨɜ ɨɛɹɡɚɬɟɥɶɧɵɯ ɪɚɛɨɬ.
(ɍɄ ɊɎ, ɋɬ. 72, ɱ.3)
Глава 3. Числа
3.1. Системы счисления
ɑɢɫɥɨ – ɞɪɟɜɧɟɣɲɟɟ ɢɡ ɦɚɬɟɦɚɬɢɱɟɫɤɢɯ ɩɨɧɹɬɢɣ. Ɉɧɨ ɪɨɞɢɥɨɫɶ ɜ ɨɬɜɟɬ ɧɚ ɧɭɠɞɵ ɩɪɚɤɬɢɱɟɫɤɨɣ, ɯɨɡɹɣɫɬɜɟɧɧɨɣ ɞɟɹɬɟɥɶɧɨɫɬɢ ɱɟɥɨɜɟɤɚ. ɇɚɱɚɥɨɫɶ ɜɫɟ ɫ ɧɚɬɭɪɚɥɶɧɵɯ ɱɢɫɟɥ, ɤɨɬɨɪɵɟ ɩɨɹɜɢɥɢɫɶ ɜ ɫɜɹɡɢ ɫ ɧɟɨɛɯɨɞɢɦɨɫɬɶɸ ɩɨɞɫɱɢɬɵɜɚɬɶ ɨɬɞɟɥɶɧɵɟ ɩɪɟɞɦɟɬɵ (ɫɤɨɬ, ɪɚɛɨɜ, ɜɨɢɧɨɜ ɢ ɞɪ.). Ɍɨɪɝɨɜɥɹ, ɩɪɢɛɵɥɶ ɢ ɞɨɥɝɢ ɩɪɢɜɟɥɢ ɤ ɢɫɩɨɥɶɡɨɜɚɧɢɸ ɰɟɥɵɯ ɱɢɫɟɥ (ɩɨɥɨɠɢɬɟɥɶɧɵɯ ɢ ɨɬɪɢɰɚɬɟɥɶɧɵɯ). Ⱦɚɥɶɧɟɣɲɟɟ ɭɫɥɨɠɧɟɧɢɟ ɩɪɨɢɡɜɨɞɫɬɜɚ, ɧɟɨɛɯɨɞɢɦɨɫɬɶ ɢɡɦɟɪɹɬɶ ɢ ɜɵɱɢɫɥɹɬɶ ɞɥɢɧɵ ɩɪɹɦɵɯ, ɩɥɨɳɚɞɢ ɩɪɹɦɨɭɝɨɥɶɧɢɤɨɜ ɢ ɨɤɪɭɠɧɨɫɬɟɣ ɩɨɪɨɞɢɥɢ ɪɚɰɢɨɧɚɥɶɧɵɟ ɢ ɜɟɳɟɫɬɜɟɧɧɵɟ ɱɢɫɥɚ.
ȼɵɞɚɸɳɢɦɫɹ ɦɵɫɥɢɬɟɥɶɧɵɦ ɚɤɬɨɦ, ɧɚɱɚɥɨɦ ɚɛɫɬɪɚɤɬɧɨɝɨ ɦɵɲɥɟɧɢɹ ɛɵɥɨ ɨɬɞɟɥɟɧɢɟ ɱɢɫɥɚ ɨɬ ɩɪɟɞɦɟɬɚ ɫɱɟɬɚ, ɤɨɝɞɚ ɜ ɜɵɱɢɫɥɟɧɢɹɯ ɫɬɚɥɢ ɨɩɟɪɢɪɨɜɚɬɶ ɬɨɥɶɤɨ ɫ ɫɚɦɢɦɢ ɱɢɫɥɚɦɢ. Ⱥ ɷɬɨ ɩɨɬɪɟɛɨɜɚɥɨ ɭɦɟɧɢɹ ɡɚɩɢɫɵɜɚɬɶ ɱɢɫɥɚ.
ɋɨɜɨɤɭɩɧɨɫɬɶ ɩɪɢɟɦɨɜ ɢ ɩɪɚɜɢɥ, ɭɫɬɚɧɚɜɥɢɜɚɸɳɢɯ ɜɡɚɢɦɧɨ ɨɞɧɨɡɧɚɱɧɨɟ ɫɨɨɬɜɟɬɫɬɜɢɟ ɦɟɠɞɭ ɱɢɫɥɨɦ ɢ ɟɝɨ ɡɚɩɢɫɶɸ, ɧɚɡɵɜɚɸɬ ɫɢɫɬɟɦɨɣ ɫɱɢɫɥɟɧɢɹ (ɧɭɦɟɪɚɰɢɟɣ).
Ʉ ɩɪɢɦɟɪɭ, ɧɚ ɪɢɫ. 3.1. ɞɥɹ ɨɞɧɨɝɨ ɢ ɬɨɝɨ ɠɟ ɱɢɫɥɚ ɬɪɢɧɚɞɰɚɬɶ ɩɪɢɜɟɞɟɧɵ ɡɚɩɢɫɢ ɜ ɪɢɦɫɤɨɣ, ɞɟɫɹɬɢɱɧɨɣ ɢ ɞɜɨɢɱɧɨɣ ɧɭɦɟɪɚɰɢɹɯ.
ɋɟɝɨɞɧɹ ɩɪɚɤɬɢɱɟɫɤɢ ɩɨɜɫɟɦɟɫɬɧɨ ɩɪɢɦɟɧɹɸɬ ɞɟɫɹɬɢɱɧɭɸ ɩɨɡɢɰɢɨɧɧɭɸ ɫɢɫɬɟɦɭ ɫɱɢɫɥɟɧɢɹ. ɋɥɨɜɨ ɞɟɫɹɬɢɱɧɚɹ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɫɱɟɬ ɩɪɟɞɦɟɬɨɜ ɜɟɞɭɬ ɞɟɫɹɬɤɚɦɢ, ɚ ɱɢɫɥɨ ɞɟɫɹɬɶ ɧɚ-
ɑɢɫɥɨ ȿɝɨ ɡɚɩɢɫɢ
XIII
13
1101
Ɋɢɫ. 3.1
30
