
Молекулярная физика (11-18)
.pdfФедеральное агентство по образованию РФ Ухтинский государственный технический университет
11
Определение поверхностного натяжения жидкости по методу максимального давления в пузырьке газа
Методические указания к лабораторной работе для студентов всех специальностей дневной и заочной формы обучения
Ухта
2007
УДК |
53(075) |
|
Ш 19 |
ББК |
22.3.Я7 |
Шамбулина, В.Н. Определение поверхностного натяжения жидкости по методу максимального давления в пузырьке газ а. [Текст]: метод. указания/ В.Н. Шамбулина, В.И. Сухарев. – Ухта: УГТУ, 2007. – 9 с.:ил.
Методические указания предназначены для выполнения лабораторной работы по физике по теме “Основы молекулярной физики и термодинамики ” для студентов специальностей 290700, 290300 и направлению 550100.
Методические указания рассмотрены и одобрены кафедрой физики от 19.02.07г., пр. № 5.
Содержание методических указаний соответствует рабочей учебной программе.
Рецензент: |
Филиппов Г.П., старший преподаватель ка федры физики |
|
Ухтинского государственного технического университета. |
Редактор: |
Северова Н.А., доцент кафедры физики Ухтинского |
|
государственного технического университета. |
В методических указаниях учтены предложения рецензента и редакто ра.
План 2007г., позиция 37 . Подписано в печать16.04.2007.
Компьютерный набор Сивенкова А. гр. ИСТ -05.
Объём 9 с. Тираж 50 экз. Заказ № 209 .
Ухтинский государственный технический университет, 2007 169300, г. Ухта, ул. Первомайская, 13.
Отдел оперативной полиграфии УГТУ. 169300, г. Ухта, ул. Октябрьская, 13.
2
ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ ЖИДКОСТИ ПО МЕТОДУ МАКСИМАЛЬНОГО ДАВЛЕНИЯ В ПУЗЫРЬКЕ ГА ЗА
Краткая теория
Жидкость по внешним признакам характеризуется текучестью (легким изменением формы), несжимаемостью и наличием свободной поверхности. В жидкостях среднее расстояние между молекулами значительно меньше, чем в газах. Поэтому силы взаимодействия между молекулами играют в жидкостях существенную роль.
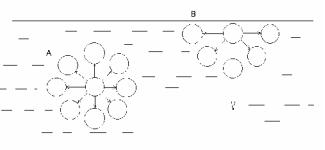
Поверхностный слой жидкости по своим свойствам отличается от внутренних частей жидкости, что обусловлено молекулярными явлениями. Молекула внутри жидкости (А) окружена другими молекулами со всех сторон, их притяжение взаимно уравновешивается, равнодействующая всех сил равна нулю. Для молекулы (В), расположенной у поверхности жидкости, сложение
всех сил дает равнодействующую, направленную внутрь жидкости. Поэтому для того, чтобы перевести молекулу из внутренних слоев в поверхностный слой, надо совершить работу против указанной равнодействующей силы.
Рис. 1 Следовательно, каждая молекула, находящаяся в поверхностном слое
обладает избытком потенциальной энергии по сравнению с молекулами, находящимися внутри жидкости. Чем больше поверхность жидкости, тем большее число молекул обладает этой избыточной потенциальной энергией. Следовательно, при увеличении поверхности некоторой массы жидкости (например, при разбрызгивании воды в мелкую водяную пыль) энергия жидкости увеличивается.
Вследствие стремления молекул уйти внутрь жидкости с ее поверхности принимает такую форму, при которой ее свободная поверхность имеет наименьшую возможную величину.
Рассмотрим такой опыт. Возьмем проволочный каркас с подвижным ребром, изображенный на рис. 2, и окунем его в мыльную воду. При осторожном извлечении каркаса из раствора на нем остается натянутой тончайшая мыльная пленка. Передвинем теперь подвижное ребро на н екоторое расстояние dx. При этом слой жидкости на каркасе растянется и несколько утончится, а его полная поверхность с обеих сторон каркаса увеличится на
dS 2ldx . |
(1) |
3
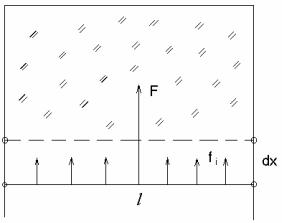
Если обозначить через n0 число
молекул, заполняющих единицу площади поверхности пленки, то при ее растяжении n0dS молекул перейдут из объема жидкого слоя на ее поверхность. Поскольку извлечение одной молекулы на ее поверхность связано с увеличением ее потенциальной энергии на W0, то для растяжения мыльной пленки придется затратить внешнюю работу:
Рис. 2
|
dA W0 n0 dS dS , |
(2) |
Величина называется коэффициентом поверхностного натяжения, или |
||
просто поверхностным натяжением данной жидкости. |
|
|
Из (2) вытекает, что |
dA |
(3) |
и dA при dS 1. |
dS |
|
|
|
|
Следовательно, |
коэффициент поверхностного натяжения |
численно |
равен работе, которую нужно совершить для увеличения поверхности жидкости на единицу площади.
В системе СИ величина измеряется в Дж/м2, в СГС в эрг/см2. Отпустим подвижное ребро каркаса и дадим ему вернуться в исходное
положение.
Тогда молекулы, вышедшие на поверхность, вернутся обратно внутрь жидкости, и внутренние силы сцепления совершат точно такую же работу
dA dS .
Микроскопическая картина сил, действующих на каждую отдельную молекулу, будет весьма сложной. Ма кроскопически это проявится в том, что на свободное ребро каркаса действует по всей линии соприкосновения его с поверхностью жидкости (длиной 2 l) результирующая сила
F fi ,
называемая силой поверхностного натяжения . Эта сила направлена касательно к поверхности жидкости и перпендикулярна к контуру, ограничивающему поверхность жидкости. Эта сила совершает работу
dA Fdx . |
(4) |
4
Сравнивая полученные два выражения (2) и (4) и учитывая (1), найдем
2ldx Fdx ,
откуда |
F |
|
|
|
|
, |
(5) |
||
2l |
||||
|
|
|
т.е. F при 2l =l. Формула (5) дает нам второе определение коэффициента поверхностного натяжения (вытекающее из первого):
коэффициент поверхностного натяжения чис ленно равен силе поверхностного натяжения, действующей на единицу длины контура, ограничивающего поверхность. В системе СИ он измеряется в Н /м, в СГС дн/см.
Измерения поверхностного натяжения показывают, что поверхностное натяжение жидкостей зависит только от природы жидкости и от ее температуры.
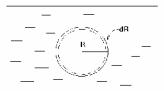
Рассмотрим пузырек воздуха, находящийся на некоторой глубине внутри жидкости. Под действием сил поверхностного натяжения жидкости он примет форму сферы радиуса R. (Рис. 3).
|
Вычислим величину добавочного давления под этой |
|
сферической поверхностью. |
|
Пусть под действием поверхностного натяжения объем |
|
пузырька уменьшился на малую величину dV. Работа |
|
сжатия пузырька будет равна: |
Рис. 3 |
dA pdV pd (4 R3 ) p4 R 2 dR . |
|
3 |
Изменение поверхностной энергии в соответствии с (2) равно работе молекулярных сил, т.е.
dA dS d(4 R2 ) 8 RdR , приравнивая правые части последних двух выражений, получим :
p4 R 2dR 8 RdR ,
откуда |
|
2 |
|
|
|
|
|
|
p |
. |
|
|
(6) |
||||
|
|
|
|
|||||
|
|
|
R |
|
|
|
|
|
Таким образом, мы вывели формулу, которая является частным случаем |
||||||||
формулы Лапласа |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|||
p |
|
|
|
|
, |
|||
|
|
|
||||||
|
R1 |
|
R2 |
|
||||
|
|
|
|
|
|
|||
где -коэффициент поверхностного натяжения жидкости, R1 и R2 – радиусы кривизны поверхности в данной точке.
5
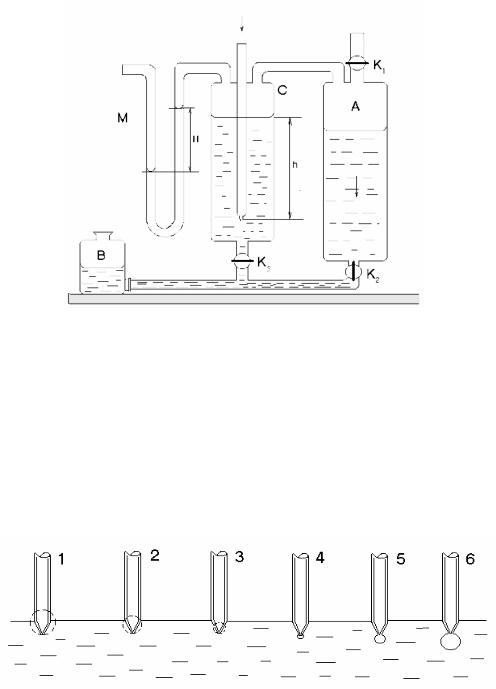
Описание установки и вывод расчетной формулы
Рис. 4
Если при закрытом кране К1 (рис. 4) слегка приоткрыть кран К2 , то вода
из сосуда А начнет медленно перетекать в сосуд В и в верхней части сосуда А, а следовательно, и в соединенных с ним сосуде С и манометре М создаетс я разрежение. При некотором определенном разрежении избыток атмосферного давления проталкивает через оттянутый кончик трубки Е в сосуд С пузырек воздуха. В процессе образования пузырька давление, измеряемое манометром, постепенно повышается, доходит до нек оторого максимального значения, а затем несколько падает. Процесс образования пузырька показан на рис. 5.
Рис. 5 Как видно из рис. 5, по мере увеличения разности давлений радиус
пузырька сначала уменьшается (1 -4), пока не становится равным радиусу кончика трубки, а затем вновь увеличивается (5,6) до тех пор, пока пузырек не отрывается.
Максимальное давление, измеренное манометром, соответствует радиусу пузырька, равному радиусу кончи ка трубки.
Если глубина погружения кончика трубки Е в исследуемую жидкость равна нулю (h=0), то давление в пузырьке согласно формуле (6) равно разности
6
атмосферного давления и давления в сосуде С, которая измеряется манометром М. Таким образом, если h=0, то
2 1 gH ,
R
где 1 - плотность жидкости в манометре,
H – разность уровней жидкости в манометре.
Если глубина, на которой образуется пузырек, не равна нулю (h 0), то давление в пузырьке для его образования должно быть больше на величину
давления исследуемой жидкости на данной глубине, т.е. на величину |
2 gh , |
||
т.е. |
2 |
2 gh 1 gH , |
|
|
R |
|
|
откуда |
|
1 1 gH 2 gh R . |
(7) |
|
|
2 |
|
Если в манометре и в сосуде С находится одна и та же жидкость, т.е. 1 |
2 , то |
формула может быть представлена в виде |
|
1 g H h R . |
(8) |
2 |
|
Полученная формула является расчетной для данной лабораторной работы. Радиус кончика трубки и род жидкости в сосуде С и в манометре М указаны на установке.
Выполнение работы
1.Открыть все краны К1, К2, К3 и, поднимая сосуд В, наполнить водой сосуды А и С.
2.Закрыть все краны К3, К2, К1, сосуд В поставить на стол.
3.Слегка приоткрыть кран К2 так, чтобы в сосуде А создавалось разрежение. Когда в сосуде С начнут образовываться пузырьки, отрегулировать открытие крана К2 так, чтобы один пузырек образовался за 1 -2 секунды.
4.Наблюдая за уровнями жидкости в манометре, записать положение каждого уровня в момент соответствующий максимальному давлению. Полученные значения H и h записать в таблицу.
5.Приоткрыть кран в сосуде С и уменьшить уровень воды в сосуде на 10 мм. Записать новые значения H и h.
6.По результатам измерений вычислить 5 -10 значений разности H и h и найти среднее значение.
7.По среднему значению разности H-h вычислить среднее значение поверхностного натяжения .
7
8. По формуле
|
|
|
2 |
|
g 2 |
|
H h 2 |
|
R 2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
g |
|
|
H h |
|
R |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
вычислить относительную и абсолютную ошибки измерения .
Таблица измерений и вычислений
№ |
H |
h |
H-h |
R |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
Контрольные вопросы
1.Что называется поверхностным натяжением? Дать определение силы поверхностного натяжения, ед. измерения в СИ.
2.Записать условие равновесия давлений для свободного пузырька, находящегося в жидкости на глубине h.
3.От чего зависит коэффициент поверхностного натяжения?
4.Записать формулу коэф. поверхностного натяжения, ед. измерения.
5.Записать формулу Лапласа в общем виде и указать 3 частных случая ее применения.
6.Явление смачивания, несмачивания; мениск, краевой угол. Записать формулу Жюрена и объяснить все величины, входящие в эту формулу. Сделать рисунок.
8
Индивидуальные задания
1.Какую энергию нужно затратить на образование поверхности мыльного пузыря радиусом 6 см при пост. tº. (Ответ: 3,6·10-3Дж)
2.
|
|
капилляр |
1) |
При каких условиях жидкость в капилляре |
|
|
|
|
займет такое положение? |
1 |
|
|
2) |
Показать направление силы поверхностного |
|
|
|||
2 |
жидкость |
|
натяжения в т.1 и в т.2. |
|
|
|
|||
|
|
|
|
|
3.Воздушный пузырек диаметром d = 0,02 мм находится на глубине h = 25 см под поверхностью воды. Определить давление воздуха в этом
пузырьке. Атмосферное давление принять нормальным. Поверхностное натяжение воды σ = 73 мН/м, а ее плотность ρ = 1 г/см3(Отв.118кПа).
4.Ртуть массой З г. помещена между двумя параллельными стеклянными пластинками. Определить силу, которую необходимо приложить, чтобы
расплющить каплю до толщины d = 0,1 мм. Ртуть стекло не смачивает. Плотность ртути ρ = 13,6 г/см3, а ее поверхностное натяжение σ =0,5 Н/м. (Отв.22 Н).
5.Две капли воды радиусом r = 1 мм каждая слились в одну большую каплю. Считая процесс изотермическим, определить уменьшение поверхностной энергии при этом слиянии, если поверхностное натяжение воды σ = 73 мН/м (Отв.378 нДж)
6.Капилляр внутренним радиусом 0,5 мм опущен в жидкость. Определить
массу жидкости, поднявшейся в капилляре, если ее поверхностное натяжение равно 60 мН/м (Отв.1,92∙10-5 кг).
7.В капилляре диаметром d = 100 мкм вода поднимается на высоту h = 30
см. Определить поверхностное натяжение σ воды, если ее плотность ρ = 1 г/см3 (Отв.73мН/м).
Библиографический список
ТрофимоваТ.И.Реальные газы, жидкости и твердые тела. / Т.И. Т.И.Трофимова//Курс физики: Учеб. М.,1998. - гл.10.,§66-69.- С.130-134.
9
Федеральное агентство по образованию РФ Ухтинский государственный технический университет
12
Определение коэффициента вязкости воздуха методом истечения из капилляра
Методические указания к лабораторной работе для студентов всех специальностей дневной и заочной формы обучения
Ухта
2007
