
Молекулярная физика (11-18)
.pdfИЗУЧЕНИЕ РАСПРЕДЕЛЕНИЯ МОЛЕКУЛ ГАЗА ПО СКОРОСТЯМ НА МЕХАНИЧЕСКОЙ МОДЕЛИ
Цель работы. Изучение распределений Гаусса и Максв елла на примере использования механической модели – доски Гальтона.
Краткая теория
В молекулярной физике часто приходится пользоваться понятием математической вероятности и среднего значения физической величины. Знакомство с этими понятиями тем более не обходимо, т.к. научное понятие о вероятности отличается от того, которым пользуются в обыденной жизни. Главное отличие состоит в том, что в науке вероятности событий можно выражать числами и сравнивать их количественно. Как находят такие числа?
1. Математическая вероятность. Рассмотрим пример с газом. Пусть объем
сосуда, в котором находится газ, равен V. Допустим, что одну молекулу газа мы как-то пометили и следим за ее перемещением. Какова же вероятность того, что
эта молекула в данный момент времени наход ится в объеме V, который является
частью объема V? Ответ на этот вопрос можно отыскать двумя способами.
1-й способ. Допустим, что у нас есть двое часов, причем одни часы обыкновенные, а другие имеют ту особенность, что идут, когда отмеченная нами
молекула находится в объеме V и останавливаются, когда она из него выходит. Установив часы на нуль, пустим их в ход на длительное время τ. Это время τ
покажут первые часы, тогда как вторые позволят узнать суммарное время t, |
в |
|
течение которого молекула находится в объеме V. Отношение |
t/τ , когда |
τ |
беспредельно возрастает, есть вероятность w появления данной |
молекулы |
в |
объеме V, т.е. |
|
|
w lim t |
|
. |
(1) |
В формуле (1) предполагается, что предел существует. Существование его несомненно, если внешние условия, в которых находится частица, со временем не изменяются. В противном случае предела быть не может: его нет, например, если газ непрерывно расширяется.
2-й способ. Если время наблюдения τ очень велико, то частица многократно
побывает во всех частях объема V. При равноправности всех частей объема |
V |
общее время пребывания молекулы в объеме V должно быть пропорционально |
|
величине этого объема. Поэтому вероятность появления молекулы в объеме |
V |
можно выразить отношением этого объема к общему объему, т.е. |
|
3
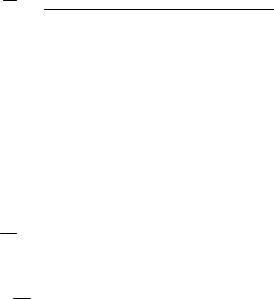
w |
V |
|
|
|
V . |
(2) |
|||
|
||||
Если V = V, то вероятность w = 1. Это значит, что молекула обязательно |
||||
находится где-то |
в объеме |
V. Таким образом, вероятность становится |
||
достоверностью, если математическая вероятность равна 1.
Математическая вероятность события всегда выражается отношением двух чисел и не может быть больше единицы.
Рассмотрим в виде примера такой вопрос. Молекулы газа, двигаясь хаотически, могут иметь всевозможные скорости. Какова вероятность того, что
численное значение скорости u данной молекулы лежит между u1 и (u1 + du)? Пусть n – общее число молекул, а dn – число молекул, скорости которых лежат между u1 и (u1 + du). Тогда искомая вероятность определится по формуле
dw dn . |
(3) |
n |
|
2. Среднее значение переменной величины . Пусть некоторая переменная |
|
величина (например, скорость молекулы) принимает |
n1 раз значение x1, n2 раз |
значение x2 и т.д., а общее число этих значений |
|
n n1 n2 n3 ..... |
(4) |
Тогда среднее значение x этой величины |
|
x n1x1 n2x2 n3x3 ..., n
или
|
|
n1 |
n2 |
n3 |
...... |
|
|
||||
x n x1 |
n |
x2 n x3 |
|||
(5)
(6)
Но n1 / n есть вероятность w1 того, что величина x принимает значение x1;
отношение n2 / n – вероятность того, что она принимает значение x2 и т.д., поэтому равенство (6) можно переписать в виде:
|
x |
w1x1 w2x2 w3x3 ...., |
|
|
|
|
i n |
т.е. |
x |
wi xi . |
|
|
|
|
i 1 |
(7)
(8)
4
Итак, среднее значение переменной величины x равно сумме произведений всех значений этой величины на вероятность того, что она принимает данное значение.
Если какая-либо величина принимает непрерывный ряд значений между 0 и ∞, то среднее значение этой величины выражается интегралом:
x xdw,
(9)
0
где dw есть вероятность того, что значение x лежит в бесконечно малом
интервале между x и (x + dx).
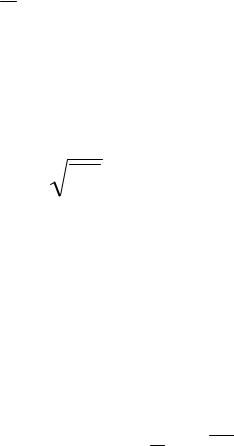
Средним квадратичным данной величины называют корень квадратный из ее
среднего квадрата, т.е. |
|
|
x0 |
x2 . |
(10) |
Для нахождения среднего квадрата можно воспользоваться формулами ( 5) –
(9). Тогда в случае, когда величина x2 принимает непрерывный ряд значений в интервале от 0 до ∞, ее средний квадрат, согласно (9), определяется по формуле:
|
|
|
|
|
x2 |
x2dw. |
(11) |
0 |
|
||
Если, возведя обе части равенства (9) в квадрат, сравнить результат с формулой (11), то станет ясно, что квадрат средней величины не равен среднему
квадрату этой величины, т.е. x 2 x2 .
Понятие о статистическом законе распределения
Нам известно, что молекулы при столкновении меняют свои скорости, но мы не можем предвидеть, с какой скоростью станет двигаться произвольно выбранная молекула в тот или иной момент времени. Мы говорим, что скорость любой молекулы в данный момент времени случайна. Однако и число молекул, скорости которых лежат в том или другом интервале скоростей, подчиняется определенному статистическому закону распределения.
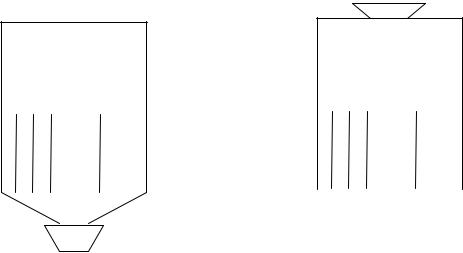
Наглядное представление о случайном явлении и о стати стическом законе дает модельный опыт с доской Гальтона (рис .1, а). В верхней части доски забиты гвоздики в шахматном порядке. Внизу расп оложены желобки одинаковой ширины. Спереди прибор закрыт стеклом. Вверху над гвоздиками укреплена воронка. Будем бросать в воронку по одной дробинке, следя за ее движением.
5
Ударяясь о гвоздики, дробинки меняют направление дв ижения и падают в какойнибудь желобок. Допустим, что первая дробинка упала в жел об 3. Вторая дробинка, конечно, будет двигаться по иной траектории и, вер оятно, упадет в другой желобок. Но может случиться и так, что и она упадет в ж елобок 3. Повторим опыт много раз, записывая, в какой желобок упадет дробинка. Вот начало записи в одном из опытов: 5, 4, 2, 3, 1, 5, 9, 3, 3, 3, 2, 1,…. Есть ли какаялибо закономерность в чередование этих чисел? Не существует ли закона, который позволил бы предсказать, в какой желоб попадет дробинка при том, или ином бросании, например, 101-м? Такого закона нет: и траектория дробинки, и столкновение ее с тем или другим гвоздиком, и попадание в тот или иной желобок – все это явление случайное.
C1
A
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
D |
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
1 2 3 4 5 6 7 8 9 |
|
||||||
1 2 3 4 5 6 7 8 9 |
||||||||||||
|
C2 |
|
|
|
а) |
|
|
|
|
б) |
||
|
|
|
|
|
|
|
|
|
||||
Рис.1. Доска Гальтона (а) и демонстрация статистического закона распределения дробинок по желобкам (б).
Поместим теперь в воронку сразу много дробинок и не станем обращать внимание на то, как при падении дробинки движутся между гвоздиками, а поинтересуемся только результатом – распределением дробинок по желобкам (рис.1, б). Оказывается, что больше всего дробинки падают в средний желобок, а в боковых ячейках, их окажется тем меньше, чем дальше желобок отс тоит от середины. При повторении опыта всякий раз получит ся одно и то же распределение, независимо от общего числа дробинок, но при непременном условии, что это их общее количество достаточно велико.
Проведем еще один опыт. Прежде чем насыпать дробинки в воронку, пронумеруем их тем или иным способом. Когда они распределятся по желобкам, сосчитаем, сколько дробинок попало в желобок 1, записав их номера. Так же поступим с дробинками, попавшими в остальные желобки. Затем перепишем все дробинки и повторим опыт. Номер дробинок в каждом из желобков будет теперь иным, но в каждом желобке окажется почти столько же дробинок, как и раньше.
Таким образом, в опыте попадание д робинки в тот или иной желобок – явление случайное, а распределение дробинок по желобкам подчиняется
6
определенному статистическому закону. Отобразим этот закон графически. Обозначим через N общее число дробинок, через
желобок 1, через N2 число дробинок, оказавшихся в желобке 2 и т.д. Найдем
отношения N1 / N, N2 / N, N3 / N…., а далее отметим, что закономерность состоит в следующем: эти отношения при повторении опытов остаются приблизительно постоянными, если число дробинок в елико.
Желобки имеют одинаковую ширину. Поэтому число дробинок в каждом желобке пропорционально высоте столбика дробинок в этом желобке.
Следовательно, |
|
|
... N1 |
: N2 |
|
N3 ... h :h |
|
|
|
|
|
|||
N |
1 |
:N |
2 |
:N |
: |
2 |
:h |
... |
. |
(12) |
||||
|
|
3 |
N |
N |
|
N |
1 |
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, графически стати стический закон распределения дробинок по желобкам изобразится ломаной линией (рис.1 , б), которую проведем по верхним границам заполненного частицами объема . Но этому графику можно приписать и иной смысл. Будем бросать в воронку одну и ту же дробинку и найдем, сколько раз из общего числа бросаний дробинка попадет в тот или иной
желобок. Пусть n1, n2, n3 и т.д. суть числа попаданий соответственно в желобки 1, 2, 3 и т.д., и пусть общее число бросаний составило n. Тогда вероятность
попадания дробинки в данный желобок будет измерятьс я отношениями n1/n, n2/n, n3/n и т.д.
Построив столбики, высоты которых пропорциональны числам
n3/n и т.д., получим график распределения вероятностей попадания одной дробинки в любой данный желобок. Если этот график сопоставить с тем, кото рый мы до этого получили для распределения множества дробинок по желобкам, то окажется, что эти графики друг от друга не отличаются.
Таким образом, один и тот же график (рис. 1, б) можно истолковать двояко: как изображение статистического закона распределения дробинок по желобкам или как изображение вероятности попадания дробинки в определенный желобок.
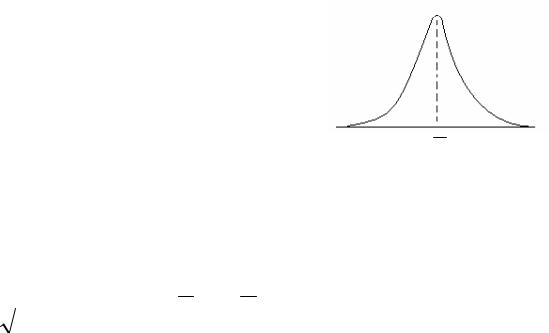
Чем уже желобки, тем более гладкой будет кривая распределения дробинок. Предельно мы получим так называемую кривую Гаусса (рис. 2), поскольку
распределение дробинок по желобкам в рассмотренных опытах описывается функцией Гаусса, которую приближенно можно записать так :
w |
|
1 |
|
ехр( (n |
n |
)2 / 2 |
n |
), |
(13) |
|
|
|
|||||||
|
|||||||||
n |
2 n |
||||||||
|
|
|
|||||||
7
где n – среднее значение величины n (в рассмотренном примере n есть число
дробинок в желобке), ехр – основание натуральных логарифмов, а wn –
вероятность данного значения n.
Кривая изображающая гауссово распределение (ее называют гауссовой или нормальной), имеет колоколообразную форму, симметричную относительно
максимума, который лежит при n n . Такой кривой описывается, например, распределение ошибок измерения, распред еление компонент скорости молекул газа, находящегося в тепловом равновесии, но сами скорости молекул распределяются по иному закону, кот орый называется максвелловским .
Закон Максвелла о распределении по скоростям для молекул идеального газа, находящегося в состоянии равновесия выражается следующей формулой:
dw dn |
4 u2 |
ехр( |
u |
)2du F(u) du, |
|
|||||
|
|
|
|
|
|
(14) |
||||
3 |
||||||||||
n |
|
uвер |
||||||||
|
uвер |
|
|
|||||||
где dw – вероятность того, что молекула имеет скорост ь в интервале между u и (u+du) , n – число молекул в единице объема, dn – среднее число молекул в
единичном объеме со скоростями между u и (u+du) , ехр – основание
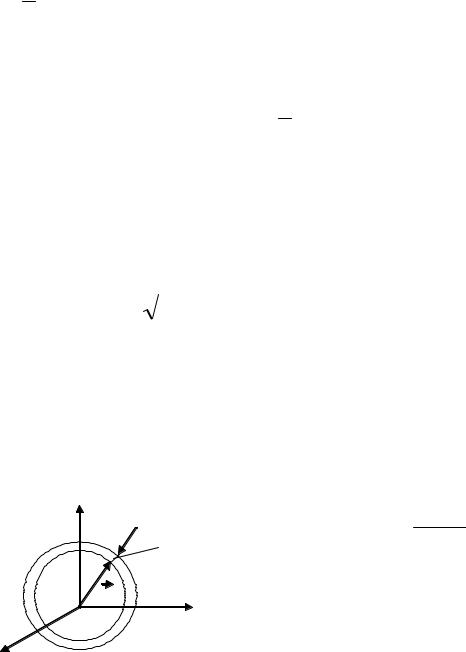
натуральных логарифмов, uвер – наиболее вероятная скорость молекулы, F(u) – максвелловская функция распределения молекул газа по модулям их скоростей .
Как следует из (14), функция распределения, равная
uz |
F(u) dn , |
(15) |
||
|
|
|
||
du |
|
ndu |
|
|
u |
представляет |
собой долю молекул, модули |
||
скоростей которых находятся в шаровом слое |
||||
uy |
||||
единичной толщины, если скорости молекул |
||||
ux |
||||
изображать в виде полярных векторов в |
||||
|
||||
Рис. 3. Трехмерное пространство |
трехмерном |
пространстве |
скоростей, в |
|
котором по взаимно перпендикулярным осям |
||||
скоростей. |
||||
координат отложены компоненты ux, uy, uz |
||||
|
скоростей молекул (рис 3). Чтобы получить |
|||
закон распределения Максвелла по абсолютным значениям скоростей, необходимо проинтегрировать по всем значениям скоростей, лежащим и внутри
тонкого шарового слоя радиусом u и толщиной du. Объем этого слоя равен
4πu2du.
Из физического смысла функции распределения следует условие нормировки для максвелловского распределения:
8
|
|
F(u)du 1. |
(16) |
0 |
|
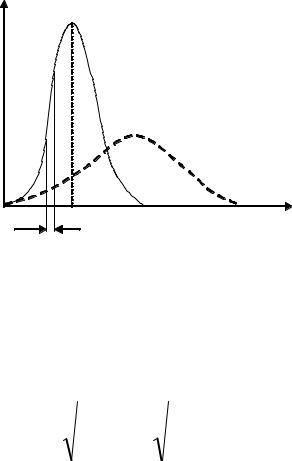
На рис. 4 изображено распределение молекул |
по скоростям для двух |
температур, причем Т1< Т2. По оси абсцисс отложены скорости, а по оси ординат функция распределения F(u). Площадь выделенной фигуры (вертикальной полоски) численно равна доле dn/n от общего числа молекул, которую образуют
молекулы со скоростями между u и (u+du). При меньшей температуре доля молекул, приходящихся на определенный интервал скоростей, больше, чем при более высокой температуре, на величину выступаю щей части узкой выделенной
полоски на рис. 4. Площадь, ограниченная |
всей кривой распределения и осью |
|||||||
абсцисс, равна единице, как при температуре Т1 так и при Т2. |
максвелловского |
|||||||
|
|
|
|
Кривые |
||||
F(u) |
|
|
распределения |
по |
скоростям |
|||
|
|
|
имеют |
следующие |
особенности: |
|||
|
Т1 |
|
они |
проходят |
через |
начало |
||
|
|
|
координат, |
асимптотически |
||||
|
|
|
приближаются к оси абсцисс при |
|||||
|
|
|
бесконечно больших скоростях, |
|||||
|
|
|
имеют максимум, асимметричны |
|||||
|
Т2 |
|
(слева от максимума кривые идут |
|||||
|
|
|
круче, чем справа). |
|
|
|||
|
|
|
То, |
что |
кривая |
максвелловского |
||
du |
uвер |
u |
распределения |
проходит |
через |
|||
начало |
координат, |
означает, что |
||||||
Рис. 4. Кривая распределения |
|
неподвижных молекул в газе нет. |
||||||
|
А |
из |
того, |
что |
кривая |
|||
|
Максвелла. |
|
||||||
|
|
асимптотически |
приближается к |
|||||
|
|
|
||||||
|
|
|
оси |
абсцисс |
при |
бесконечно |
||
больших скоростях, следует, что очень большие скорости молекул маловероятны. Скорость, которая соответствует максимуму кривой распределения, является
наиболее вероятной скоростью uвер и определяется по формуле:
|
|
|
|
|
|
|
|
, |
|
u |
2kT |
|
|
2RT |
|
(17) |
|||
|
|
||||||||
вер |
m |
M |
|||||||
|
|
|
|||||||
где k – постоянная Больцмана, R – универсальная газовая постоянная, T –
температура газа, m – масса одной молекулы, M – молярная масса вещества. Если при графическом представлении закона Максвелла по оси абсцисс
откладывать отношение скорости к наиболее вероятной (некое х = u/uвер), то для всех температур и любых масс молекул получится одна и та же кривая. Поэтому
9

при решении задач на закон распределения молекул по скоростям удобно пользоваться этой кривой, а в ее отсутствии таблицей 1 (См. приложения), в
которой даны значения N /(N u) для различных значений х.
Зная закон статистического распределения молекул по скоростям и, пользуясь предоставленной в начале работы, математической справкой, можно определить основные величины, характеризующие газ – среднюю квадратичную скорость (18) и среднюю скорость молекул (19):
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
3RT |
, |
|
|||
|
|
|
|
|||||||
u2 |
(18) |
|||||||||
|
|
|
||||||||
кв |
|
|
|
|
|
M |
||||
|
|
|
|
|
|
|
||||
|
|
. |
|
u |
8RT |
(19) |
|
cp |
M |
||
|
|
||
Из соотношений (17), (18) и (19) следует, что наиболее вероятная, средняя и средняя квадратичная скорости образуют следующую пропорцию :
uвер :ucp :uкв 1:1,1:1,2. |
(20) |
Экспериментальным подтверждением закона распределения молекул по скоростям могут служить опыт Штерна и опыт Ламмерта [2].
Описание установки
Доска Гальтона, используемая в работе, представлена на рисунке 1. В верхней части доски находятся гвоздики А зафиксированные в шахматном порядке. Внизу расположены желобки (ячейки) В одинаковой ширины (в количестве 47). Спереди прибор закрыт стеклом. Вверху над гвоздиками укреплена воронка С1. Для повторного проведения опыта желобки приемника освобождаются от шариков путем выдвигания вправо и влево горизонтальных пластин D, являющихся подвижным дном для желобков . Шарики ссыпаются в емкость для хранения по воронке С 2.
Во втором опыте используются шарики большей массы примерно в таком же количестве.
10
Порядок выполнения работы
1.Медленно высыпать через воронку шарики и, если они мелкие и в большом количестве, то измерить линейкой их уровни yi последовательно во всех ячейках приемника ( i – номер ячейки), начиная от начальной. Если используются крупные шарики, то принять за yi – их количество в конкретной ячейке. Данные занести в таблицу.
2.Сложить значения уровней шариков во всех ячейках (или их количество в отдельных ячейках). В первом случае величина yi – пропорциональна
общему числу шариков, во втором – определяет их общее количество . Записать суммарную величину в таблицу.
3.Рассчитать и занести в таблицу для каждой ячейки отношение yi / yi ,
пропорциональное вероятности Pi попадания шариков в данную ячейку при ширине ячеек, равной единице.
4.Построить график зависимости yi / yi от номера ячейки для первого опыта.
5.Освободить ячейки, предварительно подставив под нижнюю воронку емкость для шариков.
6.Аналогичные измерения проделать для шариков с большей массой, произвести расчеты по п. 1, 2, 3 и данные расчета занести на тот же график в виде второй кривой.
7.По максимумам двух кривых определить наиболее вероятные скорости
uвер и uвер (в наших условных единицах, т.е. по номеру ячейки, в
которую попало наибольшее количество шариков ) и затем отношение масс шариков:
m /m uвер2 |
/uвер2 . |
(21) |
11
Таблица измерений и вычислений
|
|
|
1 опыт |
|
|
2 опыт |
||
|
|
|
|
|
|
|
|
|
№ |
|
yi |
|
yi / yi |
|
yi |
|
yi / yi |
ячейки |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
46 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
47 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yi |
|
yi |
|
|
|
||
|
u |
2 |
|
|
2 |
|
|
|
|
вер |
|
uвер |
|
|
|||
|
|
|
|
m /m |
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы
1.Поясните, что называют математической вероятностью события.
2.Что называют средним значением переменной величины и как определить среднее значение с использованием понятия вероятность?
3.Что называют средним квадратичным величины?
4.Поясните, как, используя доску Гальтона, можно продемонстрировать статистический закон распределения случайных величин?
5.Нарисуйте кривую распределения Гаусса и поясните ее.
12
