Молекулярная физика (11-18)

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ ГАЗА ПО СКОРОСТИ ЗВУКА В ГАЗЕ

Краткая теория

Вследствие того, что молекулы идеального газа на расстоянии не взаим о- действуют друг с другом, внутренняя энергия такого газа будет складываться из энергии отдельных молекул. След овательно, внутренняя энергия одного моля идеального газа будет равна произведению числа Авогадро на среднюю энергию одной молекулы:

ί – число степеней свободы молекулы

k – постоянная Больцмана, NА – число Авогадро, число молекул в 1 моле. Внутренняя энергия произвольной массы газа m будет равна внутренней энергии одного моля, умноженной на число молей газа, содержащихся в массе

m:

R – молярная газовая постоянная.

Теплоемкостью какого-либо тела называется величина, численно равная количеству теплоты, которое нужно сообщить телу, чтобы повысить его темп е- ратуру на один градус.

большое). Размерность C равна Дж/моль·К.

Теплоемкость единицы массы вещества называется удельной теплоемк о- стью. Ее мы будем обозначать буквой c (c -малое). Размерность c равна

Дж/К··кг.

Между молярной и удельной теплоемкостью вещества имеется очевидное

М – молярная масса газа

3

Величина теплоемкости зависит от условий, при которых происходит н а- гревание тела. Наибольший интерес предс тавляет теплоемкость при постоянном объеме Cv или при постоянном давлении C p , когда нагревание происходит

при постоянном объеме или при постоянном давлении. Согласно первому началу термодинамики количество теплоты, сообщенное газу, идет на приращение внутренней энергии и на работу расширения газа.

dQ = dU + dА

Если нагревание происходит при постоянном объеме, тело не совершает работы над внешними телами и, следовательно, вся теплота идет на приращение внутренней энергии тела:

Следовательно, чтобы получить теплоемкость моля идеального газа при постоянном объеме, нужно продифференцировать по температуре выраж ение

(1) для внутренней энергии газа. Произведя дифференцирование, получим:

Как следует из этого выражения, молярная теплоемкость идеального газа при постоянном объеме оказывается постоянной величино й, не зависящей от параметров состояния газа, в частности от температуры.

Заметим, что с учетом (7) выражение для внутренней энергии 1 моля идеального газа может быть записано в следующем виде:

Uм = Сν · ∆T. (8) Если нагревание газа происходит при постоянном давлении, то газ будет расширяться, совершая над внешними телами положительную работу. Следов а- тельно, для повышения температуры газа на один градус в этом случае понад о- бится больше тепла, чем при нагревани и при постоянном объеме, т.к. допол нительно теплота будет затрачиваться на совершение газом работы. Поэтому те п- лоемкость при постоянном давлении должна быть больше, чем при постоянном

объеме на работу расширения.

4

Напишем уравнение первого начала термодинамики для одного моля га-

за:

Слагаемое dUdTм дает, как мы видим, молярную теплоемкость газа при

постоянном объеме. Поэтому формула (10) может быть записана следующим образом:

Дифференцируя это выражение по T ( p const ), находим:

Таким образом, работа, которую совершает один моль идеального газа при повышении его температуры на один градус при постоянном давлении, оказывается равной молярной газовой постоянной.

Отметим, что соотношение (12) получено с использованием уравнения идеального газа и, следовательно, справедливо только для идеального газа.

С учетом формулы (7) можно получить для C p следующее выражение:

5

Поделив (13) на (12), найдем характерное для каждого газа отношение C p к Cv :

Как следует из (14), величина определяется числом и характером степ е- ней свободы i . При жесткой связи молекул учитываются только поступател ь- ные и вращательные степени свободы. Так ка к, в составе воздуха кислород О2 и азот N2 (2-х атомные газы), принимаются i in iвр 3 2 5

Звуковые волны в газах и жидкостях являются продольными. В твердых телах могут распространятся как продольные, так и поперечные звуковые во л- ны. Скорость их распространения (скорость звука) зависит от упругих свойств среды и плотности и определяется формулой :

где - плотность среды, E - модуль продольной упругости.

Процесс распространения звуковых волн в газах схематически можно представить следующим образом: источник механических колебаний передает эти колебания окружающим его газовым молекулам: в результате изменяется давление газа в данной микрообласти пространства. Так как газ обладает упр у- гими свойствами, то он немедленно расширяется и в данном элементарном объеме газа образуется разрежение, а микрообласть повышенного давления п е- ремещается несколько дальше от источника звука и т.д. Процессы сжатия и разряжения протекают очень быстро, поэтому изменение давления газа прои с- ходит без теплообмена.

Так как для газов модуль продольной упругости связан с давлением соо т- ношением:

Выразив из уравнения Клапейрона – Менделеева:

6

Таким образом, для определения отношения теплоемкостей газа надо и з- мерить температуру газа и определить скорость звука в газе.

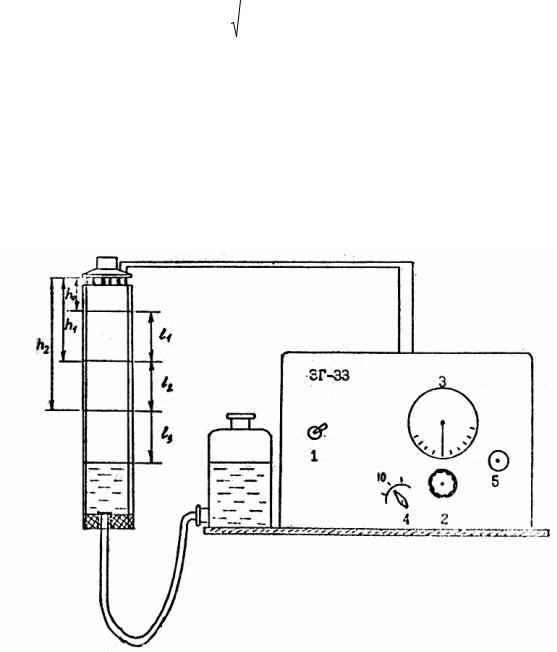
Установка для определения скорости звука в газе (рис. 1) состоит из звукового генератора, динамика и вертикальной трубы с водой, уровень которой можно менять с помощью соединенного с ней сосуда.

Рис. 1.

Звуковой генератор заставляет колебаться мембрану динамика с опред е- ленной фиксированной частотой . В результате возникают звуковые волны определенной длины , которые распространяются во все стороны от динам и- ка.

7

Звуковая волна, отраженная поверхностью воды в трубе возвращается о б- ратно к мембране динамика. В ре зультате амплитуда колебаний мембраны или увеличивается или уменьшается.

Усиление колебаний мембраны произойдет в том случае, если отраженная волна подойдет к плоскости мембраны в той же фазе, в которой находится в данный момент времени сама мембрана. Совп адение фаз сопровождается заметным усилением звука.

Пусть уровень воды в трубе находился в самом верхнем положении. При медленном опускании уровня можно заметить несколько его положений ( h0 , h1, h2 и т.д.), при которых происходит усиление звук а. Очевидно, что расстояние l между ближайшими уровнями усиление звука равно половине длины волны, т.к. усиление колебаний происходит только тогда, когда разность хода 2-х волн равна целому числу длин волн.

Таким образом, для определения длины волны , соответствующей данной частоте , необходимо определить расстояние между двумя ближайшими уровнями воды, дающими усиление звука, и удвоить его, т.е. 2l , где:

l h1 h0 h2 h1 h2 h2 ...

Скорость звука υ может быть определена через частоту и длину волны п о- средством соотношения:

Выполнение работы

Целью работы является определение отношения теплоемкостей для во з-

духа.

Работа выполняется в следующей последовательности:

1.Тумблером 1 «сеть» включить звуковой генератор и подо ж- дать 2-3 минуты, пока он прогреется.

2.Ручкой установки частоты 2 установить на круглой частотной шкале 3 одну из частот, заданных преподавателем в диапазоне 600 -1200

8

Гц. Для этого при положении переключателя множителя 4 в положении 10 установить против неподвижного штриха одно из чисел из инт ервала 60-120. С учетом множителя 10 это и будет заданная частота выну ж- денных колебаний мембраны динамика.

3.После того, как прибор прогреется, ручкой «Регулятор вых.» 5 установить минимальную громкость звука с тем, чтобы не мешать о с- тальным работающим в лаборатории.

4.Изменяя уровень воды в трубе от самого низкого до самого высокого и наоборот, найти и записать в таблицу высоту воздушного столба ( h0 , h1, h2 ), при которой громкость звука заметно возрастает. З а-

пись высот производить начиная с наибольшей высоты.

Т.к. для измерения длины волны берется абсолютное значение разности высот h1 h0 , h2 h1 и т.д., то не имеет значения где находится нулевая отметка шкалы. Отсчет можено вести как от динамика так и от любого конца трубы.

5.Закончив измерения с одной частотой, перейти на следу ю- щую и повторить измерения высот в той же последовательности.

6.Проведя все измерения, выключить звуковой генератор тумблером «сеть».

7.Измерить и записать в таблицу температуру воздуха вблизи установки.

8.По данным таблицы найти отрезки l1,l2 ,l3... и вычислить их

среднее значение.

9.По формуле (21) вычислить для каждого опыта. Найти среднее значение .

10.По формуле:

вычислить относительную погрешность δ затем и абсолютнуюср по результатам одного из опытов.

9

Контрольные вопросы

1.Дайте определение теплоемкости тела и удельной теплоемкости вещества.

2.Как связаны удельная и молярная теплоемкости?

3.Что такое Cp иCv ?

4.Почему всегда больше единицы?

10

5.Каково ожидаемое значение для воздуха, если считать, что

воздух представляет собой смесь двухатомных газов?

6.К какому типу волн относятся звуковые волны?

7.Объясните назначение воды в данной работе.

Индивидуальные задания

1.Вычислить удельные теплоёмкости cp и cv газов: 1) гелия; 2) водорода; 3) углекислого газа. Ответ : 1) 3,12 кДж / ( кг · К ), 5,29 кДж / ( кг · К ); 2) 10,4 кДж / ( кг · К ), 14,6 кДж / ( кг · К ); 3) 567 Дж / ( кг · К ), 756 Дж / ( кг · К ).

2.Разность удельных теплоёмкостей cp - cv некоторого двухатомного газа равна 266 Дж / ( кг · К ). Найти молярную массу М газа. Ответ : 0,032 кг / моль.

3.Каковы удельные теплоёмкости cp и cv смеси газов , содержащей ки-

. Найти : 1) количество теплоты Q , сообщенное газу; 2) изменение ∆U внутренней энергии ; 3) совершённую газом работу А . Ответ: 67 кДж, 0

6.При изохорном нагревании кислорода объёмом V = 50 л давление газа изменилось на ∆р = 0,5 МПа. Найти количество теплоты Q , сообщенное газу. Ответ : 62,5 кДж.

7.Воздух массой m = 29 г нагрели на ∆Т = 200 К, причем газу было передано количество теплоты Q = 10 кДж. Найти изменение ∆U внутренней энергии газа и совершенную им работу А . Ответ : 4,2 кДж; 6,8 кДж.

Библиографический список

Трофимова Т.И. Курс физики: – M.: Высшая шк. 2000. – Гл.9., § 50-54.

11