49. Как определить напряжения при действии равномерно распределённой нагрузки под центром прямоугольника? Напишите формулы.

Рис. Сжимающие напряжения под центром и под углом прямоугольника с равномерно распределённой нагрузкой.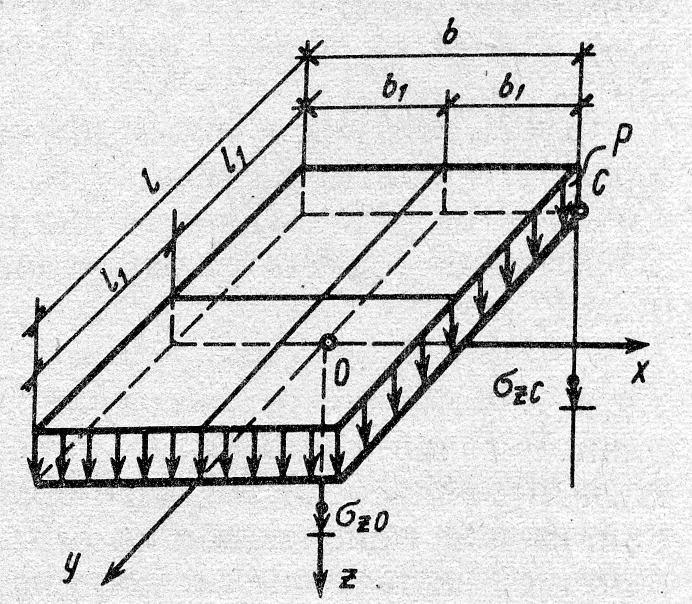

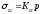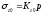; , (6.26)

где K_zс и K_z0 - соответственно коэффициенты влияния для угловых и центральных напряжений, зависящие от соотношения сторон загруженного прямоугольника и относительной глубины точка, в которой определяются напряжения.

;

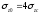
Коэффициент α зависит от безразмерных параметров т и п. Параметр 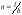для обоих случаев является одинаковым. При определении углового напряженияσ_zс параметр m=z/b; при определении напряжения под центром прямоугольника σ_z0 параметр m=2z/b. Значения коэффициентов α приведены в табл.

50. Как определить напряжения при действии равномерно распределённой нагрузки под углом прямоугольника? Напишите формулы.

51.Какие безразмерные координаты приняты в нормах (СНиП) для расчёта напряжений?

Для расчета напряжений в нормах (СНиП) приняты две относительные координаты x и h , причем и,где b - ширина (наименьшая сторона) подошвы прямоугольного фундамента, l - его длина (всегда l³ b).

52. Начертите схему эллипсов главных напряжений при полосовой нагрузке.

Рис. 6.11. Линии равных напряжений (изобары) σ_z , (распоры) σ_x , (сдвиги) τ_xz при действии равномерно распределённой полосовой нагрузки.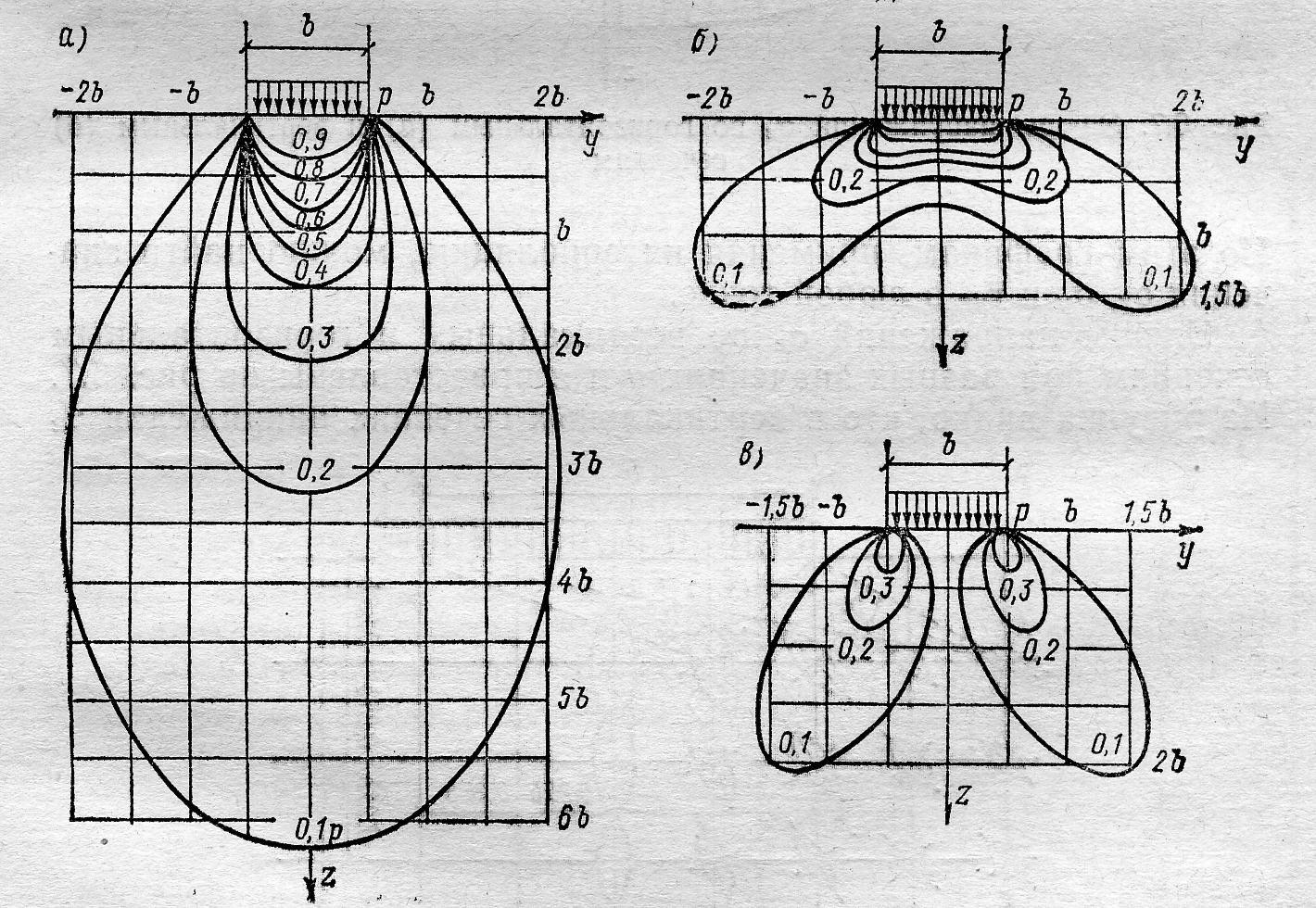

53. Каким образом, зная эпюру напряжений σz вдоль оси zпри равномерно распределённой полосовой нагрузке, действующей на участке шириной b, построить эпюру σz, если нагрузка будет действовать в пределах участка шириной 2b? Как будет трансформироваться эпюра σz при дальнейшем увеличении ширины участка, в пределах которого она расположена?

Если имеется эпюра напряжений σ_z при ширине загруженного участка b, то, зная ординату σ_z на глубине z, нужно эту же ординату для случая ширины 2b отложить на глубине 2z и т.д. (рис.М.8.9).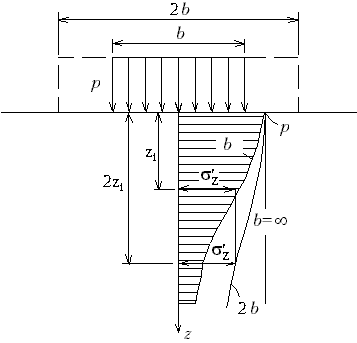

При дальнейшем росте ширины загруженного участка напряжения будут все медленнее рассеиваться и при увеличении b до бесконечности эпюра σ_z будет иметь постоянную ординату σ_z =p. Все эти эпюры имеют верхнюю ординату, равную p, и выходят поэтому из одной точки.

54. Каким образом будет трансформироваться эпюра вертикальных напряжений σz в случае, если одна и та же равномерно распределённая нагрузка на поверхности приложена в пределах квадрата, прямоугольника, ленты при одной и той же ширине b?

Чем больше длина l (наименьшая сторона называется шириной b, поэтому всегда l³ b), тем "полнее" эпюра напряжений σ_z (рис.М.8.10).

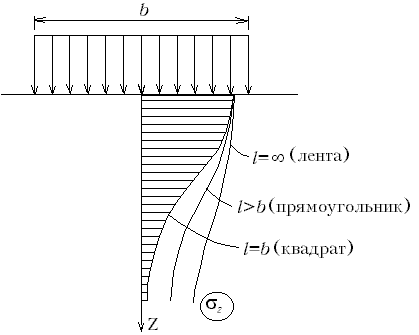
55. Как определить напряжения методом угловых точек? Основные схемы. Формулы.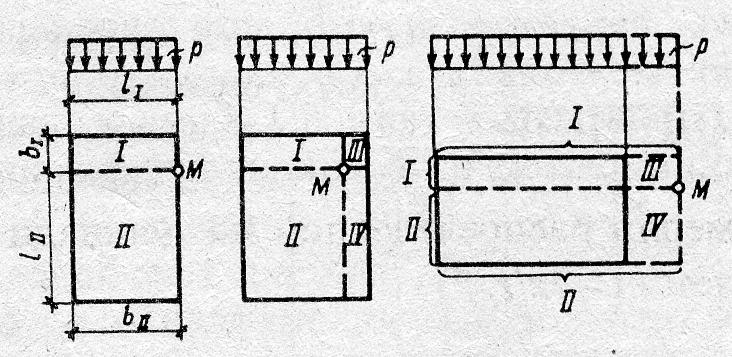

Здесь возможны три варианта решения (рис. 6.14).

Пусть вертикаль проходит через точку М, лежащую на контуре прямоугольника. Разделив этот прямоугольник на два так, чтобы точка М являлась угловой для каждого из них, можно представить напряжения σ_zM как сумму угловых напряжений I и II прямоугольников, т. е. .

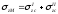Рис. 6.14. Схема для расчёта напряжений методом угловых точек.

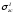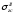Соответственно значения напряжения иопределяются п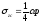о. Коэффициентыα^I и α^II находятся из табл. по значениям безразмерных параметров l_I/b_I, z/b_I и l_II/b_II, z/b_II, где, l_I, b_I, l_II, b_II - размеры сторон соответствующих прямоугольников. При этом всегда принимается, что .

Если точка М лежит внутри контура прямоугольника, то его следует разделить на четыре части так, чтобы эта точка являлась угловой для каждого составляющего прямоугольника. Тогда

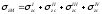. (6.30)

Наконец, если точка М лежит вне контура загруженного прямоугольника, то его нужно достроить так, чтобы эта точка вновь оказалась угловой. Тогда, полагая, что напряжения в точке М возникают от действия нагрузки, распределенной по площади прямоугольников I и II, необходимо вычесть напряжения от действия той же фиктивной нагрузки, распределенной по площади прямоугольников III и IV, т. е. действительное напряжение определится выражением

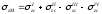. (6.31)