Глава 8 НЕЛІНІЙНІ СИСТЕМИ АВТОМАТИЧНОГО КЕРУВАННЯ
И-.(0) = " ' - « " ;
І+ <г,0 (Дм,Ео )И',(0)
Жя . ( 0 ) - передаточна функція частини системи між точками прикла-
дання сигналів є0 і Р0.
Для гармонічної складової система рівнянь повністю збігається з (8.81), (8.82). Отже, і в цьому разі для визначення трьох невідомих Д со, є0 є три рівняння (8.81), (8.82) і (8.84).
Якщо характеристика нелінійної ланки несиметрична, то рівнян-
ня (8.84) слід замінити |
рівнянням |
|
є0 = - |
Ж л (0)Л(Л 0), Єр)+ |
(8.85) |
Вимушені рухи, зумовлені гармонічними вхідними сигналами. При гармонічних вхідних сигналах можливі два варіанти поведінки системи. У першому припускається, що автоколивання в системі відсутні, тобто вони або принципово неможливі, або зовнішні дії такі, що режим автоколивань не виникає. У цьому разі для аналізу динаміки системи можна користуватися гармонічно лінеаризованими передаточними функціями нелінійних ланок.
Якщо ж у системі існують автоколивання і до неї прикладена зовнішня гармонічна дія, то або відбудеться «захоплювання», тобто автоколивання будуть придушені і в системі встановиться рух з частотою зовнішньої дії, або одночасно існуватимуть два види рухів: автоколивання і вимушені коливання.
Розглянемо спочатку вимушені рухи за відсутності автоколивань. Нехай структурна схема системи має вигляд, зображений на рис. 8.29, причому гармонічно лінеаризована передаточна функція
IVИЛ (А) нелінійної ланки |
є |
функцією тільки амплітуди А. Вхідний |
сигнал /(/) = А 8 іп |
Де |
|
шо |
~~ |
амплітуда і |
частота зовнішньої |
гармонічної дії. |
|
|
|
|
|
|
|
Відповідно до структурної схеми, зображеної на рис. 8.29, сигнал |
на вході нелінійної ланки |
|
|
|
|
|
|
|
£(0= |
, |
н / |
' |
н . 7 Г |
№. |
(8-86) |
|
|
І |
+ Жнл (А)1УЯ (р) |
|
Складність визначення вимушеного руху є(/)за рівнянням (8.86) полягає в тому, що для його визначення треба знати передаточну функцію И/ІШ (А), а вона, своєю чергою, залежить від А, де А = |є|.
8.10. Дослідження автоколивань методом гармонічної лінеаризації
Розглянемо ОДИН ІЗ МОЖЛИВИХ ІЄ''
і рафічних способів розв'язування рівняння (8.86). Задаючи різні значення амплітуди А і викорисювуючи формулу гармонічної чи іеаризації конкретного непнійного елемента, за формулою (8.86) при р= усо0 розраховуємо іалежність | є | = /{(А) (рис. 8.37). Гочка перетину графіка цієї залежності з бісектрисою | є | = /4 визначає амплітуду вимушених коливань Аа.
Фазу сигналу є можна знайти гак само, як і для лінійних сис-
іем, попередньо визначивши \¥НЛ(А) при
|
1 |
£/(а)0) + уГ(со0) |
|
і + ^ К Г Л л ) |
|
|
Ф = агсі£
г / К ) "
Отже, сигнал 8 визначається повністю: є(ґ) = А а 8ІП (со0/ + ф).
Розглянемо тепер вимушені рухи в системі з автоколиваннями. Нехай, як і раніше, структурна схема системи має вигляд, зображений на рис. 8.29, причому
|
|
\уя{р)= |
(р)- |
|
^„л |
= |
^нл (Аг ,р)=К2 (Аг, |
р)Ю2 |
(А£, р), |
де А£ — амплітуда вимушених коливань, яку треба визначити. |
Зовнішня дія |
має |
вигляд /(ґ) = А0 $іп со0/. |
Знаходимо розв'язок |
для 8(/)у формі |
|
|
|
|
|
|
є(ґ) = А£ 8Іп (а>пґ - |
ф£ ) . |
(8.87) |
Подамо зовнішню дію /(/) у такому вигляді: |
ДО = А0 |
8іп со0ґ - А0 зіп [(со0ґ - фЕ) + фе ] = |
Глава 8 НЕЛІНІЙНІ СИСТЕМИ АВТОМАТИЧНОГО КЕРУВАННЯ
|
= А0 |
8Іп (со0/ - фЕ)соз фе + А0 С08 (оо0/ - фь.)8Іп фЕ. |
(8.88) |
З рівняння |
(8.87) дістанемо |
|
|
|
|
|
|
|
|
8іп ( ш 0 ґ - ф е ) = є ( 0 / Л є . |
|
|
(8.89) |
Здиференціювавши |
(8.89), визначимо |
|
|
|
|
|
со8 (со0ґ - Ф£ ) = рг/А^щ. |
|
|
(8.90) |
Підставимо значення 8Іп (оо0/ - фЕ) і С08 (со0ї - Фе ) в (8.88), тоді |
|
ДО = (АО соз фе)Є(/)/у4е |
+ (А0 8Іп Фе)/?8/ЛеСО{) . |
(8.91) |
Згідно зі структурною схемою, наведеною на рис. 8.29, |
|
е(0_ |
|
1 |
_ |
|
|
0,Ш2(4,Р) |
|
/(() |
1 |
+ К (р)№нл (Ае, р) |
о, |
Ш2 {А, ,р)+Яі (р) |
К2 (Ае, |
р)' |
звідки |
|
|
|
|
|
|
|
|
|
|
|
КЛР)Я2(АЄ, |
р)]- |
/ Ш І р Ш А , , |
р)= 0. |
(8.92) |
Після підстановки в це рівняння значення /(/) за формулою |
(8.91) отримаємо |
|
|
|
|
|
|
|
|
є(ґ) ( /?, |
(р) Я2 (Ас ,р) |
+ 0І |
Шг (А - |
Р) х |
|
|
|
|
1 - |
А0 соз фЕ |
рАа |
зіп фЕ |
= 0. |
|
(8.93) |
|
|
|
Д. |
Аеш0 |
|
|
|
Рівняння (8.93) є однорідним диференціальним рівнянням, коефіцієнти якого залежать від невідомих величин Ае і <ре, а також відомих величин Ап, о)0 і параметрів системи.
Характеристичне рівняння має вигляд
Д(Ае ,р)= Я, (р) К2 (Ае ,р)+0І Шг (А, Р) х
1 А0 соз фЕ |
рАи зіп фс = 0. |
|
Аею„ |
У системі встановлюються коливання з частотою со(), якщо це рівняння справедливе при р= уа>0, тобто якщо виконується умова
Я, (М>) Я2 (/1,, у'со0) + £>, (усо0 )02 (Ае, > 0 ) х
Контрольні запитання та завдання
1 _ А0 соз ф£ _ Л0 зіп фе = 0. |
(8.94) |
Рівність (8.94) можлива, якщо дорівнюють нулю її дійсна і уявна частини. Тому, подавши цю рівність у вигляді
Х(А0, ш0 , ЛЕ, <ре) + у'У(А0, о)0, Д,, <ре) = 0,
дістанемо два рівняння з двома невідомими АЕ |
і фє: |
Х(А0,ш0,АЕ,(рЕ)=0; |
(8.95) |
Г(Л0,(о0,Ае,(Ре)=0. |
(8.96) |
Якщо система рівнянь (8.95) і (8.96) має дійсні додатні розв'язки, і о умови захоплення виконуються і автоколивання у системі будуть придушені.
З рівнянь (8.95) і (8.96) можна знайти залежності АЕ і ф£ від ампмі іуди А0 і частоти со0 вхідного сигналу, а також від параметрів системи. Найбільший інтерес становить залежність мінімального значення амплітуди А0тіп, за якого ще виконується умова захоплення, від частоти со0. Залежність Л0тіп = /(ш0 ) називається пороговою частот-
ною характеристикою.
Умови захоплення дають змогу визначити, якими зовнішніми діями можна придушити небажані автоколивання і вибрати такі з них, за яких у системі встановлюються вимушені коливання з допустимими амплітудою і частотою.
Контрольні запитання та завдання
1.Що розуміють під нелінійною системою? У чому полягає принципова різниця між лінійними і нелінійними системами?
2.Перелічіть основні типові нелінійні характеристики і наведіть їх математичний опис.
3.Яка структурна схема нелінійної системи називається найпростішою? Як привести до найпрос-
тішої структурну схему будь-якої замкнутої нелінійної САК, що містить одну нелінійну ланку?
4.Дайте визначення таким поняттям: фазовий простір, зображуюча точка, фазова траєкторія.
5.Що таке автоколивання?
6.Як побудувати фазовий портрет нелінійної системи другого порядку?
Глава оцінка якості,
п корекція і синтез * нелінійних систем
а в т о м а т и ч н о г о керування
9.1
Оцінка якості нелінійних САК
Для оцінки якості перехідних процесів у нелінійних САК можна використовувати показники, аналогічні показникам якості лінійних систем, а саме тривалість перехід-
ного процесу (тривалість регулювання), перерегулювання або максимальне відхилення в перехідний період, коливальність перехідного процесу. Особливість нелінійних систем виявляється в тому, що показники якості залежать від величини зовнішньої дії. Тому для повної оцінки якості необхідно виконати розрахунки перехідних процесів для всіх можливих реальних значень вхідних сигналів і збурюючих дій. Крім того, важливим є визначення умов виникнення автоколивань і обчислення їхніх параметрів.
Наближену, але досить точну оцінку якості нелінійної системи можна дістати без розрахунків перехідних процесів. Для цього, зокрема, використовується показник коливальності.
Розглянемо нелінійну систему, структурна схема якої зведена до найпростішої (див. рис. 8.2). Вона складається з лінійної частини, що має частотну передаточну функцію \¥я (уш), і нелінійної ланки з нелінійною статичною характеристикою ф(є). Застосувавши гармонічну лінеаризацію, запишемо передаточну функцію нелінійної ланки у вигляді
Жнл {а) = кТ{а) + ]к'Т{а).
Як і у лінійних системах, показником коливальності для гармонічно лінеаризованої системи є максимальне значення ординати амплітудної характеристики замкнутої системи Мт а х за початкової ординати, що дорівнює одиниці, тобто
М = |І^з(Уш,а)|тах,
Глава 9 |
ОЦІНКА ЯКОСТІ, КОРЕКЦІЯ І СИНТЕЗ |
|
НЕЛІНІЙНИХ СИСТЕМ АВТОМАТИЧНОГО КЕРУВАННЯ |
де І¥:і(уоо, а) — частотна передаточна функція замкнутої системи. При гармонічній лінеаризації використовуються так звані нормо-
вані коефіцієнти кг(ос) і к[{ос), де а = а/с —відносна амплітуда; с — характерне значення є на статичній характеристиці нелінійної ланки (див. рис. 8.1).
Значення нормованих коефіцієнтів гармонічної лінеаризації для типових нелінійних ланок, статичні характеристики яких зображено на рис. 8.1, визначаються за такими формулами:
характеристика із зоною нечутливості (див. рис. 8.1, а)
/сг(ос)=0 |
при а < 1; |
|
|
при |
а > 1; |
кн |
=1§а; |
( 9 . 1 ) |
характеристика із зоною насичення (див. рис. 8.1, б)
кг(ос) = кі{ |
п р и |
а < 1; |
|
|
при ос > 1; |
ки |
=18 ос; |
( 9 . 2 ) |
релейна характеристика (див. рис. 8.1, в)
( 9 . 3 )
характеристика з люфтом (див. рис. 8.1, г)
кГ( а) = — |
— + агсзіп (і - |
2 |
• |
|
ті |
2 |
а |
осу а |
у г |
/ |
2 ' |
|
( 9 . 4 ) |
|
|
71 ОС |
|
|
кн |
а; |
|
|
|
9.1.Оцінка якості нелінійних САК
релейна характеристика із зоною нечутливості (див. рис. |
І, д) |
кг(ос) = 0 |
при |
а < 1; |
|
к'М) = кп |
2Ла |
- |
при ос > 1; |
(9.5) |
|
ос |
|
|
|
кн = 2Ь/пс |
при |
а > |
1; |
|
характеристика реального релейного елемента (див. рис. 8.1, є)
кг(а) |
= кп |
л / а ^ ї , |
|
|
а |
к'г(а)=-ки/а2; |
(9.6) |
кИ |
=4Ь/пс. |
Передаточна функція нелінійної ланки при використанні нормованих коефіцієнтів гармонічної лінеаризації
ИГт(а) = кг(а) + ]к'г(а). |
(9.7) |
Відповідно до структурної схеми, наведеної на рис. 8.2, запишемо
Жл(усо)Жнл(ос) Ж3(усо,ос) = 1 + ^ л ( > ) ^ н л ( о с )
Якщо ввести поняття оберненої передаточної функції нелінійної ланки
2(а)= 1 / Г н л ( а ) , |
(9.8) |
го вираз для ИК,(/со, а) можна записати так:
|
а) |
К І М ) |
|
|
= 2 ( а ) + ІУЛ ( » |
|
Передаточні функції |
Осо) і І(а) подамо у вигляді суми дійсної |
та уявної частин: |
|
|
|
|
О а ) ) = £ / ( ш ) + у Г ( с о ) ; |
|
|
2(а) = г + у/"(а). |
(9.9) |
Глава 9 |
ОЦІНКА ЯКОСТІ, КОРЕКЦІЯ І СИНТЕЗ |
|
НЕЛІНІЙНИХ СИСТЕМ АВТОМАТИЧНОГО КЕРУВАННЯ |
Тоді показник коливальності М записуємо у вигляді
М = ГзС/со, а)|= Щ ї С =.
+ <V)2 + V' + У)
Піднесемо в квадрат ліву і праву частини цієї рівності:
|
М2(г + И)2 |
+ М2(г' + V)2 |
= II2 + У2; |
|
|
(.М2 - 1)£/2 |
+ ( М 2 |
- 1 )У2 |
+ М2г2 + 2М2 гІІ + М2г'2 |
+ 2М2г'У = 0. |
Поділимо всі члени останньої рівності на М2 - 1, а також додамо |
і віднімемо член М4/(М2 - |
І)2. Тоді |
після деяких математичних пе- |
ретворень дістанемо |
|
|
|
|
|
|
|
гМ2 |
|
ҐМ_ |
2 Л |
(г2 + г У ) М 2 |
|
V |
+ М2 |
- 1 |
V + М2 |
- 1 |
( М 2 - |
І)2 |
(9.10) |
або |
|
( і / - ( / 0 ) 2 + ( У - У 0 ) 2 |
|
|
(9.11) |
|
|
Я2. |
|
Звідси випливає, що для заданих сталих значень М і а рівнянню (9.11) у комплексній площині відповідає коло з радіусом Я і координатами центра (1/0, і:У0). Координати центра і радіуса дістають безпосередньо з порівняння виразів (9.10) і (9.11). їх можна також знайти як функції нормованих коефіцієнтів гармонічної лінеаризації, визначивши г і г' через к і к'г за допомогою виразів (9.7), (9.8) і (9.9). У результаті
|
гМ2 |
кг |
М2 |
|
М2 - 1 |
к2 + к'2 М2 - Г |
|
г'М2 |
К |
М2 |
|
М2 - 1 |
к2г + к'2 М2 - 1 |
|
М |
1 |
м |
к = 472 |
+г'2 м2 |
1 ф<2 + к ; 2 |
М2 і |
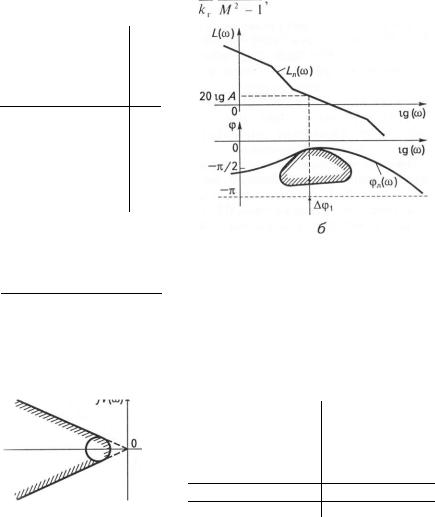
Якщо прийняти показник коливальності незмінним (М = сопзї), то для різних значень відносної амплітуди дістанемо сім'ю кіл. Заборонена зона, що відповідає бажаному показнику коливальності, створюється лініями, дотичними до цих кіл (рис. 9.1, а).
У найпростішому випадку, коли нелінійна характеристика однозначна і симетрична відносно початку координат (непарна), кое-
9.1.Оцінка якості нелінійних САК
фіцієнт к[ дорівнює нулю, отже, Г' = 0\У0 =0. Тоді радіус кола, що відповідає М = с о т і , обчислюється за формулою
'м
уУ(со)
0
| о ,
V |
№ © ) ' |
|
Ф |
|
|
|
|
|
|
и2 |
0 |
і д И |
|
|
|
|
|
ятЩтяя. |
|
|
|
|
|
|
|
Ф;
. ' / / / V / / / / / / / / / / / / / / / / / / / / / ,
Афтах]
—п
Рис. 9.1