
Teoriya avtomatichnogo keruvannya
.pdf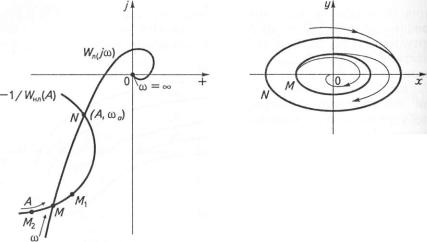
Глава 8 |
НЕЛІНІЙНІ СИСТЕМИ АВТОМАТИЧНОГО КЕРУВАННЯ |
а |
б |
|
Рис. 8.31 |
фазовій площині (рис. 8.31, |
б). Цикл М має меншу амплітуду, цикл |
N — більшу. |
|
Для перевірки стійкості граничних циклів можна скористатися критерієм Найквіста. Лінійна система перебуває на межі стійкості, якщо АФХ розімкнутої системи проходить через критичну точку з координатами (-1, у'О), тобто рівняння, що відповідає незатухаючим
коливанням, |
|
1 + |
= 0. |
Для нелінійної системи це рівняння має вигляд 1 +Жл Ош)^н л (А) = 0,
тому критичними точками для АФХ будуть точки -1 /Жил (.А), які належать від'ємній зворотній характеристиці нелінійної ланки. Охоплення чи неохоплення цих точок амплітудно-фазовою характеристикою свідчитиме про стійкість або нестійкість руху, що відповідає граничному циклу.
Розглянемо граничний цикл, що відповідає точці перетину М. Припустимо, що амплітуда трохи більша, ніж у точці А/, і значення
440
8.10.Дослідження автоколивань
~методом гармонічної лінеаризації
функції -1 /)¥1{Л(А) визначається точкою М{. АФХ лінійної частини
• • -плює цю точку, отже, рух нестійкий і амплітуда зростатиме. Якщо амплітуда стане трохи меншою, ніж у точці М(точка М2), то АФХ не ич<шлюватиме цю точку, рух буде стійким, амплітуда зменшуватиметься. Це означає, що граничний цикл М нестійкий, оскільки в шюх випадках фазові траєкторії віддаляються від нього. Якщо так са- і«> розглянути точку IV, то можна дійти висновку, що вона відповідає
і і ііікому граничному циклові. Отже, можна сформулювати таке пра-
ж ц ю |
в и з н а ч е н н я |
стійкості |
к о л и в а н ь : |
якщо |
тонка на |
кривій -1 /]¥ил (А), |
|
иіо |
відповідає |
зростаючій амплітуді, |
не охоплюється |
АФХ лінійної час- |
|||
тини |
системи, |
то |
коливання |
стійкі, а |
якщо |
охоплюється — то нестій- |
|
кі 5а цим правилом точка М відповідає нестійким коливанням, а іичка N — стійким. Знайшовши точку N1 визначимо параметри авто- і олпвань: амплітуду А (за характеристикою нелінійного елемента) і частоту соа (за АФХ лінійної частини системи). Після знаходження параметрів автоколивань слід перевірити гіпотезу фільтра (див. п. 8.9).
Якщо характеристики \¥л (уоо) і - 1 /ИКнл (А) не перетинаються, то
аіноколивання неможливі, |
а система може бути стійкою або нестій- |
і ою. Якщо АФХ лінійної |
частини не охоплює характеристику не- |
пнійного елемента, то система стійка, якщо охоплює — нестійка. Використовуючи графіки У/л (усо) і -1 /\¥нл (А), досліджуємо вплив
на частоту і амплітуду можливих автоколивань параметрів нелінійної і піки і лінійної частини системи. Зміна параметрів лінійної частини ісформує частотну характеристику ]¥л (уоо), а нелінійної ланки — харак і еристику -1 /]¥ИЛ (А).
и П р и к л а д 8.5. |
Визначити методом Гольдфарба амплітуду та частоту |
автоколивань вихідної координати слідкувального електропривода, |
|
розглянутого в |
прикладі 8.2. Структурну схему системи зображено на |
рис. 8.11. Параметри електропривода: кл = 1,5 1 /В • с; Тм = 0,1 с; = 0,1. Характеристика Ф(Є)Є характеристикою реального релейного елемента (див. рис. 8.1, б-) з такими параметрами Ь = 100 В; с = 0,25 рад.
Р о з в ' я з а н н я . Передаточна функція лінійної частини системи відповідно до структурної схеми, наведеної на рис. 8.11,
яКЮ Р(Т„Р+1) р(0,1р+1)
Передаточна функція гармонічно лінеаризованого нелінійного елемента
441

Глава 8 |
НЕЛІНІЙНІ СИСТЕМИ АВТОМАТИЧНОГО КЕРУВАННЯ |
|
|
\ут(А) = кг + |
к;Р, |
|
|
Ш |
де згідно з табл. 8.2
= 4Ь_ 1- пА
к ' = -
4Ьс пА2
Підставивши р = у'ш в передаточну функцію, дістанемо
АЬ
|
|
. 4Ьс |
4Ьс |
- 1 - у |
||
яА |
А1 |
] лА2 |
я А2 |
|||
|
||||||
|
|
пс |
|
|
|
|
|
|
"4Ь |
|
|
|
|
|
кп1 |
_ |
К&Е* |
|
|
|
|
>(/ш Тм + |
1) |
ту + |
1 ] ту + Ш |
||
= і/л(со)+уГл(ш).
|
0 |
|
СО = ОО |
|
|
+ |
|
- і / и и и ) |
/ |
|
М — с~ 0,25 |
. — |
/4=0,51 |
|
|
^/со0= 18,01
1/ ^л(усо)
со//
Рис. 8.32
+
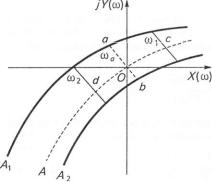
Графіки функцій -1 / Ц г т ( А ) \ И^С/со) зображено на рис. 8.32. Уявна частина
характеристики |
|
/]Ут(А) не |
залежить |
||||
від |
амплітуди, |
тому |
характеристика |
||||
А = с = 0,25 |
|
|
|
|
|
||
|
|
" І |
/К,(А) |
= |
- ^ Ь . |
|
|
|
У точці |
перетину |
характеристик |
||||
-1 /Жнп{А) |
і РУЛ(усо) |
їхні |
уявні |
частини |
|||
однакові, |
тобто |
|
|
|
|
||
|
|
|
У^лЮ^Уту |
|
|||
|
|
|
|
|
|
4Ь |
|
або |
|
|
|
|
|
пс |
|
|
|
|
2 а |
|
л |
|
|
|
|
Т У |
+ со |
4/?' |
|
||
звідки |
|
|
|
|
|
|
|
= |
4Ькдд/пс. |
|
|
|
|
(8.68) |
|
442
8.10.Дослідження автоколивань
~методом гармонічної лінеаризації
Після підстановки значень параметрів дістанемо рівняння
0,0 Іо^ + |
- 76,4 = 0, |
розв'язавши яке визначимо частоту автоколивань. Це рівняння має один дійсний додатний корінь 18,01, отже, сой = 18,01 с 1 .
Амплітуду автоколивань А визначимо з умови, що при ш = соа дійсні частини характеристик -1 /ІУІІЛ(А) і И^(усо) однакові, тобто
|
|
= |
Кят* |
4 |
ь\г |
|
г>2а + г |
Після підстановки |
значень |
параметрів дістанемо рівняння |
|
0,00196Л/І6у42 |
- 1 |
= 0,00353, |
|
звідки А = 0,51 рад.
Коливання в системі стійкі, оскільки при зростанні амплітуди точки па характеристиці -1 / І У ^ А ) кривою Жл(уш) не охоплюються.
Для перевірки умови фільтра не обов'язково будувати амплітуд- по-частотну характеристику лінійної частини. Достатньо визначити модуль характеристики
|Жл(усо)|
при со = со„ = 18,01 с"1 і со = Зсой = 54,03 с"1.
Найближчою вищою гармонікою є третя, оскільки характеристика нелінійного елемента симетрична відносно початку координат і, отже, парні гармоніки відсутні.
При со = (о„ = 18,01 с"1 | Ж л ( > Л = 0,00404, а при ш = Зсод | Жл (/3шв )| = 0,000505.
Амплітуда третьої гармоніки становить 12,5 % від амплітуди першої гармоніки, тому результат розрахунку є наближеним. Його точність можна оцінити, порівнявши з результатами прикладу 8.2.
Знайдені значення А і — це амплітуда і частота коливань на вході нелінійної ланки. Частота автоколивань однакова для всіх координат систем, включаючи 0ВПХ (див. рис. 8.12). Амплітуда коливань вихідної координати згідно зі структурною схемою також дорівнює амплітуді сигналу на вході нелінійної ланки, тому що Д01ШХ(О = - є ( / ) . Отже, частота і амплітуда коливань вихідної координати дорівнюють відповідно 18,01 с"1 і 0,51 рад.
Метод Гольдфарба можна поширити й на випадок, коли система ї й кілька нелінійних ланок. Нехай, наприклад, структурна схема ні іеми має вигляд, зображений на рис. 8.33, де передаточні функції
443

Г л а в а 8 |
НЕЛІНІЙНІ СИСТЕМИ АВТОМАТИЧНОГО КЕРУВАННЯ |
Рис. 8.33
IVип] (Д ) і Жнл 2 (А2) нелінійних ланок залежать лише від амплітуд А1 і А2 сигналів на їх входах.
Відповідно до структурної схеми
Звідси випливає, що амплітуда А2 залежить від амплітуди А1 і частоти со, тобто А2 = А2(А1, со). У цьому разі рівняння (8.66) набуває вигляду
|
Жл, С/со)Жнл, (А, )ЖЛ2 (»И/1 Ш 2 (Л,, со) = -1. |
(8.69) |
|
Позначивши |
|
і |
|
|
|
о)=1Гнл(АІ,ю), |
|
з |
(8.69) дістанемо рівняння |
|
|
^ л ( » = -1/И/и л і (Д,со), |
(8.70) |
яке відрізняється від (8.67) тим, що IVИЛ є функцією двох параметрів |
||
Д |
і со. |
|
Рівняння (8.70), як і (8.67), можна розв'язати графічно. Проте розв'язування ускладнюється, оскільки Жнл1 (Д, со) залежить від двох параметрів. Тому крім характеристики IVл (у'со) слід побудувати сім'ю характеристик -1 /И^нл1 (А)для різних частот со, (рис. 8.34, я) або сім'ю характеристик -1/Й^ил1 (у'со) для різних значень амплітуди Д (рис. 8.34, 6). Параметри можливих автоколивань визначаються точками перетину тих кривих, у яких збігаються точки з однаковими частотами.
Таким самим методом можна дослідити систему з одним нелінійним елементом, лінеаризована передаточна функція IVнл (А, оо) якого залежить від амплітуди та частоти.
444
8.10.Дослідження автоколивань
~ методом гармонічної лінеаризації
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
с°2 |
чс°1)с |
0 |
(В = 0 0 + |
|
/ |
0 |
со =оо 4- |
С 0 |
3 \ Х / \ |
|
|
|
|
|
|
|
|
|
|
А ч |
^ |
|
|
« Т І |
|
|
|
|
<0 П |
|
|
|
|
О |
|
|
б |
||
|
|
|
Рис. |
834 |
|
|
|
Метод Попова. В основу цього методу покладено кри- н'ріїі Михайлова, що дає змогу досліджувати системи з нелінійними і,піками, лінеаризовані передаточні функції яких IVИЯ (у'оо, А) зале- і ІІТЬ не тільки від амплітуди, а й від частоти. Крім того, цим методом можна досліджувати нелінійні системи з кількома нелінійними і.піками, що розділяються лінійними інерційними ланками (див.
рис. 8.33).
Розглянемо структурну схему, наведену на рис. 8.29. Прийняв-
ши, що |
Я(р)/0(р) і IVШ1 = 1¥НЛ(А, /?), в и з н а ч и м о передаточну |
функцію замкнутої системи
У . С Р ) - |
< * |
> > = |
т}КЛАр) |
|
і + Ш і у ( а о ) |
о ( р ) + т ^ ( А , Р ) |
|
|
Оір) |
" |
|
і і; і пишемо характеристичний поліном
0(р)=<2(р)+ К р ) ^ (А, р).
( 8 . 7 1 )
(8.72)
Межа коливальної стійкості визначається умовою (8.65), тобто
<2(М + К(МІУнп (А, М = 0. |
(8.73) |
445
Глава 8 НЕЛІНІЙНІ СИСТЕМИ АВТОМАТИЧНОГО КЕРУВАННЯ
Виділивши у виразі (8.73) дійсну і уявну частини, дістанемо
Х(А,и)+ у У ( Д ш ) = 0 . |
(8.74) |
Ця рівність можлива, якщо дійсна і уявна частини дорівнюють нулю, тому рівняння (8.74) можна записати у вигляді двох рівнянь з двома невідомими:
т с о ) = 0 ;
Г(Л, со)= 0.
Розв'язавши ці рівняння, знайдемо параметри автоколивань А і Амплітуда і частота є додатними дійсними числами. Тому якщо в результаті розв'язування рівнянь (8.75) обидва невідомих будуть додатними дійсними числами, то автоколивання можливі. Якщо ж будь-яке невідоме буде від'ємним або уявним, то автоколивань у
системі не існує.
Якщо вирази для коефіцієнтів гармонічної лінеаризації кг і к[ нескладні і лінійна частина системи має невисокий порядок, то систе-
му рівнянь можна розв'язати аналітично і визначити А і |
в явному |
||||
вигляді. |
|
|
|
|
|
Після визначення параметрів автоколивань необхідно перевірити |
|||||
їхню стійкість за допомогою нерівності |
|
|
|||
дХ] |
(дГ\ |
_ ґдХЛ (дУ_ |
> 0. |
(8.76) |
|
дА |
ЛЗсоЛ, |
І З с о І Л М |
|||
|
|
||||
В цьому виразі частинні похідні обчислюються для режиму автоколивань, тобто після визначення частинних похідних від дійсної та уявної частин Дусо) замість А і СДА треба підставити їхні значення. Якщо при цьому нерівність (8.76) виконується, то автоколивання стійкі, в противному разі — нестійкі.
•Приклад 8.6. Визначити методом Попова частоту і амплітуду автоколивань вихідної осі слід кувального електропривода, розглянутого в прикладі 8.5.
Р о з в ' я з а н н я . Передаточна функція лінійної частини системи
К (р)" |
М |
К(Р) |
р(ТиР+ і) |
0(Р) |
446
8.10.Дослідження автоколивань
методом гармонічної лінеаризації
а гармонічно лінеаризованої нелінійної ланки
К М Р) = пА4 Ь |
(?_ 4Ьс р |
Характеристичний поліном згідно з формулою (8.72) запишемо
гак:
П(р) = ТМІ? + р+клд |
46 |
1 - |
4Ьс р |
|
пА |
|
А* " |
Підставивши в цей вираз р = усо, визначимо дійсну і уявну частини полінома Душ) і складемо систему рівнянь вигляду (8.75):
|
|
|
4Ь_ |
с2 |
.46с |
|
м 2 |
д |
|
пА 1 - |
|
|
|
А» = -Г ш |
+ УШ+/:<7 |
|
|
|
||
со) |
= - 7 > 2 |
+ |
^ЩіЖ^г |
= |
0; |
(8.77) |
|
|
71/1 |
|
|
|
|
|
|
|
я/ґ |
|
|
(8.78) |
|
|
|
|
|
|
|
З виразу (8.78) визначимо |
|
|
|
|
|
|
|
= |
4к^Ьс |
|
|
(8.79) |
|
|
|
|
|
|
|
|
іпідставимо в (8.77). Після перетворень дістанемо рівняння
Г> 3 + со - 4клдЬ/пс = 0,
яке збігається з (8.68), знайденим у прикладі 8.5 при розв'язуванні задачі методом Гольдфарба. Розв'язок цього рівняння дає частоту автоколивань = 18,01 с_ | . Амплітуду автоколивань визначимо з виразу (8.79) при со= 18,01 с~!:
А = |
4кядЬс |
= |
14 • 1,5- 0,1 • 100- 0,25 = 0 ^ |
|
V яш |
^ |
тс-18,01 |
||
Стійкість знайденого періодичного розв'язку перевіримо за допомогою нерівності (8.76). Знайдемо частинні похідні
дХ_ |
_ 4кадЬ |
2с2 - А2 |
|
дХ_ |
дА |
П |
АЧА1-г |
' |
= - 2 7 > ; |
|
||||
|
аХ = |
8к^фс. |
д¥_ |
1. |
|
дА |
пА3 |
Зш |
|
|
|
4 4 7
Глава 8 |
НЕЛІНІЙНІ СИСТЕМИ АВТОМАТИЧНОГО КЕРУВАННЯ |
При А = 0,51 і со = 18,01
Умова (8.76)
(-43,73)-1 - (-3,602)- 72,02 = 215,7 > 0
виконується, отже, автоколивання в системі існують.
Параметри коливань вихідної осі визначають так само, як і в при кладі 8.5.
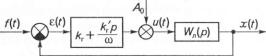
Якщо вирази для коефіцієнтів гармонічної лінеаризації досип, складні, а лінійна частина системи має високий порядок, то розв'я зок системи рівнянь (8.75) можна знайти графоаналітичним спосо бом. При цьому Х\ У розглядають як прямокутні координати і буду ють годографи вектора Михайлова Душ), змінюючи частоту у межах 0 < ш< оо для різних значень амплітуди А. Годограф вектора Михай лова, що проходить через початок координат комплексної площини, задовольняє системі рівнянь (8.75). Значення частоти, за якого годо граф проходить через початок координат, дорівнює частоті автоко ливань, а амплітуда Д для якої побудовано цей годограф, — ампліту ді автоколивань.
Практично для визначення А і о)„ немає потреби будувати сім'ю годографів для великої кількості амплітуд. Звичайно достатньо побу дувати два годографи для таких амплітуд А{ і А2, щоб один із годогра фів охоплював, а інший не охоплював початок координат (рис. 8.35).
Значення А |
і со„ визначаються |
||
з криволінійного |
чотирикутника |
||
(за умови, що А{ |
> А2) за форму |
||
лами |
ьо/А -А2у9 |
||
|
А = А- |
||
|
= со, |
сО, |
|
|
|
- М|). |
|
|
|
ССІ |
|
Стійкість |
автоколивань пере |
||
віряється так. Якщо за додатного |
|||
приросту амплітуди годограф век |
|||
тора |
Михайлова |
відповідає стій |
|
кій |
системі, |
то й |
автоколивання |
Рис. 8.35 |
стійкі. |
|
448
8.10. Дослідження автоколивань методом гармонічної лінеаризації
Системи з нелінійними елементами, що мають несиме-
тричні характеристики. Структурна схема системи у цьому разі має вигляд, зображений на рис. 8.36 (структуру нелінійної ланки подано відповідно до рис. 8.27, б). У спектрі вихідного сигналу нелінійного елемента навіть за відсутності зовнішньої дії (/(/)= 0)буде постійна ( кладова А0, яку зображено на структурній схемі у вигляді зовнішньої дії. Величина Ац визначається за формулою (8.50).
Рівняння для постійної складової у цьому разі
X о = Л ^ л ( 0 ) = - е 0
або |
|
є0 = -А0ЦҐЛ (0). |
(8.80) |
Для гармонічної складової залишається справедливою передаточна функція (8.71) і умова (8.73). Різниця полягає у тому, що в зв'яз-
ку з наявністю постійної |
|
||
складової значення А0, кГ |
|
||
і к\ |
будуть |
функціями |
|
трьох |
параметрів: в0 = |
|
|
-х0, |
А і со, тобто рів- |
|
|
ня ння |
(8.75) |
матимуть |
Рис. 8.36 |
вигляд |
со, |
є 0 ) = |
0; |
(8.81) |
Х(А, |
||||
У(А, |
со, |
є 0 ) = |
0, |
(8.82) |
а рівняння (8.80) — |
|
|
|
|
80 = —А0(А, ш, Є0 )УУл (І)). |
(8.83) |
|||
Отже, для визначення трьох невідомих А, со, є0 є система трьох рівнянь (8.81), (8.82), (8.83).
Системи з постійною зовнішньою дією. Якщо у довільній точці нелінійної системи прикладено постійну зовнішню дію то на вході нелінійної ланки з'явиться постійна складова. Якщо ха-
рактеристика нелінійного елемента симетрична відносно початку координат (непарна характеристика), то внаслідок гармонічної лінеаризації нелінійний елемент можна описати рівнянням (8.59), у якому коефіцієнти кг0, кГ і к[ є функціями трьох параметрів А, со, є0 .
Для постійної складової справедливим є рівняння
е0 = ^ з 0 ( 0 ) ^ 0 , |
(8.84) |
1 5 Теорія автоматичного керування |
4 4 9 |
