Если функция f (x) непрерывна на отрезке [a, b], то выполняются сле-
дующие свойства:
1) f (x) ограничена на [a, b], то есть
C > 0 : f (x) ≤ C, x [a, b];
2) f (x) принимает свои наибольшее M и наименьшее m значения на
[a, b];
3) |
f (x) принимает все промежуточные значения μ между |
|||
есть существует такая точка c [a, b], в которой |
f (c)=μ. |
|||
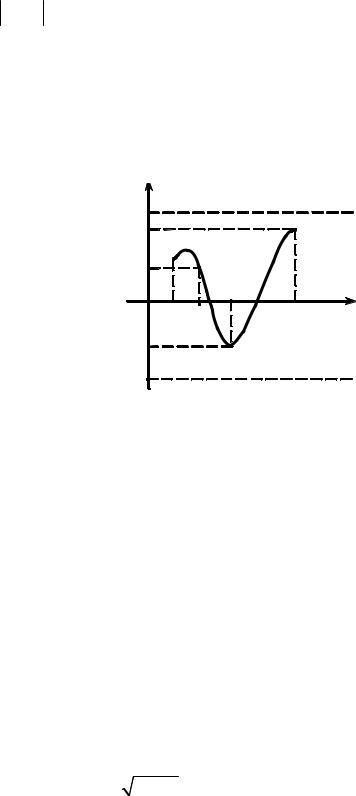
Геометрическая иллюстрация приве- |
y |
|||
дена на рис. 3.1.1. |
|
C |
||
|
M |
|||
1) |
График функции лежит |
в полосе |
μ |
|
(−C,C). |
|
|
x1 |
|
2) |
Изображен случай, когда |
f (x1 )= m , |
O a c |
|
m |
||||
|
|
|
||
f (b)= M . |
−C |
|
m и M , то
y = f (x)
b x
3) f (c)=μ, m <μ < M . |
РИС. 3.1.1 |
3.2.Контрольные вопросы
1)Сформулируйте определение непрерывной в точке функции.
2)Сформулируйте второе определение непрерывной в точке функции.
3)Что называется пределом слева и справа функции f (x) в точке x0 ?
4)Сформулируйте необходимое и достаточное условие непрерывности функции в точке.
5)Что называется точкой разрыва функции?
6)Сформулируйте свойства непрерывных функций.
7)Сформулируйте свойства функции, непрерывной на отрезке.
3.3.Практическое задание для самостоятельной работы
Вычислить пределы.
1) а) lim |
3х2 −5х − 2 |
б) lim |
2х2 −3х +1 |
в) |
|
х2 − 4 |
г) |
|
4х + 3 2х−3 |
||||||
2х |
2 |
− х − 6 |
3х |
2 |
+ х + 4 |
lim |
|
|
lim |
|
|||||
1 − |
4х −3 |
||||||||||||||
x→2 |
|
x→∞ |
|
|
x→−2 |
|
x→∞ |
4х −1 |
|||||||
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
||
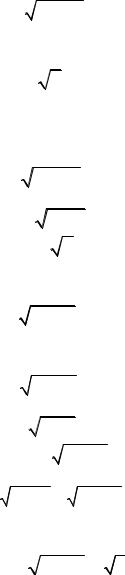
2) а) lim |
4х2 − 7х + 3 |
|
|
б) |
|
|
|
|
5х2 − 2х + 2 |
|
в) lim |
|
|
2x + 3 −3 |
|
г) lim |
5х −1 2x+1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
2х |
+ х −1 |
|
|
|
2х |
|
+ х −3 |
|
|
|
|
х |
2 |
−9 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
x→−1 |
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
x→3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
5х + 4 |
||||||||||||||||||||||||||||||||||||||||||
3) а) |
|
|
2х2 −9х + 9 |
|
б) |
|
|
|
3х2 −5х + 4 |
|
в) lim |
|
|
|
х − 2 |
|
|
|
|
г) |
|
2х − 7 4x+1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
||||||||||||||||||||||||
х |
|
−5х + 6 |
|
|
|
|
|
х |
− х +1 |
|
|
х − |
6х + |
8 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
x→3 |
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
x→4 |
|
|
|
|
|
|
|
|
x→∞ 2х −3 |
|||||||||||||||||||||||||||||||||||||||||||||
4) а) |
|
|
5х − х2 − 4 |
|
б) |
|
|
|
2х2 + х − 4 |
в) |
|
|
|
|
|
|
|
|
|
x +1 |
|
|
|
|
|
|
г) |
|
4х +1 1−2x |
|||||||||||||||||||||||||||||||||||||||||||||
lim |
х |
2 |
|
− 2х −8 |
|
lim |
|
|
|
|
|
|
|
|
|
х − 4x |
2 |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
3 + |
|
|
|
|
3х + 7 − |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x→4 |
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
x→−1 |
|
|
|
|
|
|
x→∞ |
4х − |
3 |
||||||||||||||||||||||||||||||||||||||||||||||||
5) а) |
|
|
|
|
|
|
x2 − 2x −8 |
|
|
|
б) lim |
|
|
3х2 + 5х + 4 |
в) lim |
|
|
|
х + 3 − 2 |
г) lim |
5х − 2 3−2х |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2x |
2 |
+ 5x + 2 |
|
|
|
|
2 |
х |
− х |
+1 |
|
|
|
|
|
|
х −1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
x→−2 |
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
x→1 |
|
|
|
|
|
|
|
x→∞ |
5х + |
3 |
|||||||||||||||||||||||||||||||||||||||||||||||||
6) а) |
|
|
3х2 − 2х −1 |
б) |
|
|
|
2х2 − 2х +1 |
|
в) lim |
|
|
|
|
х2 − х − 2 |
|
|
|
|
г) |
|
6х − 7 3х+2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
lim |
|
|
2 |
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|||||||||||||||||||||||
х |
− 4х + |
3 |
|
3х |
2 |
|
+ 4х + 2 |
|
|
|
|
|
4х +1 − |
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x→1 |
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
x→2 |
|
|
|
|
|
|
|
x→∞ 6х + 4 |
|||||||||||||||||||||||||||||||||||||||||||||||||
7) а) |
|
|
|
|
|
|
6 − х − х2 |
|
|
|
|
б) lim |
|
3х2 + х − 6 |
|
в) lim |
|
|
|
|
|
х2 − 25 |
|
|
|
|
|
г) |
|
2х + 3 х+1 |
||||||||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|||||||||||||||||||||||
|
3х |
2 |
+ 8х |
− 3 |
|
2х |
|
− х + 2 |
|
|
|
|
2х −1 −3 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x→−3 |
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
x→5 |
|
|
|
|
|
|
x→∞ 2х +1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
8) а) lim |
|
|
|
|
|
х2 − 3 |
|
|
|
б) |
|
|
|
х2 − 3х + 4 |
в) |
|
|
|
|
|
|
|
|
1 − x − 2 |
|
|
г) |
|
х +1 |
−х+1 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
− 4х −1 |
2 |
х |
2 |
|
+ 5х −1 |
|
4 − |
|
1 − 5x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
x→1 5х |
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
x→−3 |
|
|
|
|
|
|
x→∞ |
х −1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
9) а) lim |
|
х2 + 2х −8 |
б) lim |
3х2 − 2х −1 |
в) lim |
1+3х − 2х+6 |
г) lim |
х − 2 1−х |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
8 − |
х |
3 |
|
|
|
|
|
2 |
|
− |
|
7 |
|
|
|
|
|
х |
2 |
−5х |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
x→2 |
|
|
|
|
|
|
|
|
|
|
x→∞ 5х |
|
|
|
|
х − 2 |
|
x→5 |
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
х + |
3 |
||||||||||||||||||||||||||||||||||||||||
10) а) lim |
|
|
|
2х2 +5х−3 |
б) lim |
|
|
8х2 − 3х + 9 |
в) lim |
|
|
2х −1 − 5 |
|
г) lim |
х + 5 2х−3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
+11х+ |
6 |
|
|
2х |
2 |
|
+ 2х + |
5 |
|
|
|
|
|
х −3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
x→−3 3х |
|
|
|
x→∞ |
|
|
|
|
|
x→3 |
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ х + |
8 |
|||||||||||||||||||||||||||||||||||||||||||||||||
21