15)Какие виды асимптот существуют?
16)Какой вид имеет уравнение вертикальной асимптоты и как его найти?
17)Какой вид имеет уравнение наклонной асимптоты?
18)Запишите формулы для нахождения наклонной асимптоты.
19)Сформулируйте общую схему исследования функции.
Тема 6. Исследование функций двух переменных
6.1. Вопросы для самостоятельного изучения
6.1.1. Экстремумы функции двух переменных, необходимое условие экстремума
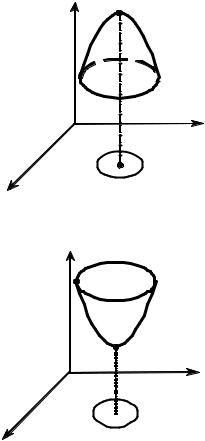
Точка P1 (x1, y1 ) называется точкой мак-
симума функции z = f (x, y), если выполняется неравенство f (P1 ) > f (P) для любой точки
P(x, y) из некоторой окрестности точки
P1 (x1, y1 ) (Рис. 6.1.1).
Точка P2 (x2 , y2 ) называется точкой ми-
нимума функции z = f (x, y), если выполняет-
ся неравенство f (P2 )< f (P) для любой точки
из некоторой окрестности точки
P2 (x2 , y2 ) (Рис. 6.1.2).
z |
zmax |
|
z = f (x, y) |
|
0 |
|
y |
|
|
|
|
|
P ( x , y ) |
||
x |
1 |
1 |
1 |
|
|
|
|
РИС. 6.1.1
z
z = f (x, y)
zmin
0 y x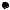 
P2 (x2 , y2 )
РИС. 6.1.2
Точки максимума и минимума называются точками экстремума функции. Значения z(x1, y1 )= z(P1 )= zmax , z(x2 , y2 ) = z(P2 ) = zmin называются соответственно максимальным и минимальным значениями функции.
41
Необходимое условие экстремума. Если точка P0 (x0 , y0 ) является точ-
кой экстремума дифференцируемой функции z = f |
(x, y), то частные производ- |
|||||||||||||||
ные функции в этой точке равны нулю |
∂z (P )= 0, |
∂z (P )= 0 . |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
∂x |
0 |
|
∂y |
0 |
|
|
|
6.1.2. Достаточные условия экстремума |
|
|
|
|
|
|
||||||||||
Рассмотрим функцию |
z = f (x, y) |
|
и пусть точка P0 (x0 , y0 ) |
является кри- |
||||||||||||
тической точкой функции, то есть |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
∂z (P )= 0 , |
∂z (P )= 0 . |
|
|
|
|
|||||||||
|
|
∂x |
|
0 |
|
|
|
|
∂y |
0 |
|
|
|
|
|
|
Предположим, что существуют все вторые частные производные |
|
|
||||||||||||||
|
∂2 z , |
∂2 z |
, |
|
∂2 z |
в точке P (x , y |
). |
|
|
|||||||
|
∂ 2 |
|
∂x ∂y |
|
|
|||||||||||
|
∂ 2 |
|
|
|
|
|
0 |
0 0 |
|
|
|
|||||
|
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составим из вторых производных выражение |
|
|
|
|
|
|||||||||||
|
|
|
|
∂ |
2 z |
|
∂2 z |
|
∂2 z |
2 |
|
|
|
|
||
|
|
= |
|
|
2 |
|
|
2 |
− |
|
. |
|
|
|
||
|
|
∂ |
|
∂ |
∂x ∂y |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
y |
|
|
|
|
|
|
|||
Чтобы ответить на вопрос, |
будет ли критическая точка P0 (x0 , y0 ) точкой |
|||||||||||||||
экстремума, необходимо исследовать знак |
(P0 ). |
|
|
|
|
|||||||||||
Теорема (достаточное условие экстремума) |
|
|
|
|
||||||||||||
Пусть P0 (x0 , y0 ) – критическая точка функции z = f (x, y). Тогда: |
||||||||||||||||
1) если |
(P )> 0 , то P – точка экстремума, причем, если |
∂2 z |
(P )> 0 , то |
|||||||||||||
|
||||||||||||||||
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
∂x2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P – точка минимума, если |
∂2 z |
(P )< 0 , то P – точка максимума; |
|
|||||||||||||
|
|
|||||||||||||||
0 |
|
∂x2 |
|
0 |
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) если |
(P0 )< 0 , то P0 – не является точкой экстремума; |
|
|
|||||||||||||
3) если |
(P0 )= 0 , то имеем неопределенный случай. |
|
|
|||||||||||||
6.1.3.Схема исследования функции z = f (x, y) на экстремум:
1.Найти частные производные ∂∂xz , ∂∂yz , составить и решить систему
42