Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский кооперативный институт (филиал РУК)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

080100Экономика(МатАнализ и ЛинАлгебра) / ЗаданияСР_МА_080100.pdf

Скачиваний:

Добавлен:

26.02.2016

Размер:

690.03 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2221 22 > Следующая >>>

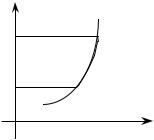
2. Если криволинейная трапеция имеет основание на оси Oy , то есть ограничена прямыми y = a , y =b , x = 0 , x = x(y) и вращается вокруг оси Oy (рис. 8.1.3),

то объем полученного тела вращения находится по формуле

V = π∫x2 ( y)dy .

y b

a	x = x(y)
0	x
	x
	РИС. 8.1.3

8.1.9. Несобственные интегралы с бесконечным верхним пределом интегри-

рования
Пусть функция y = f (x)	непрерывна на бесконечном отрезке [a,∞). Вы-
	t
берем произвольно t [a, ∞) и рассмотрим определенный интеграл ∫ f (x)dx .
	a
Несобственным интегралом от функции y = f (x) на промежутке [a,∞)
называется
∞	t
∫ f (x)dx = tlim→∞ ∫ f (x)dx .
a	a

Если предел существует, то несобственный интеграл называется сходящимся, если не существует, то расходящимся.

Для вычисления несобственного интеграла существует формула НьютонаЛейбница

∞	∞ = F (∞)− F (a),
∞
∫ f (x)dx = F (x)		(9)
a	a
где F (∞)= lim F (x), а F (x) – первообразная функции f (x).
x→∞

8.2.Контрольные вопросы

1)Сформулируйте определение определенного интеграла.

2)Перечислите свойства определенного интеграла.

3)Запишите формулу Ньютона-Лейбница.

4) Какой вид имеет формула интегрирования по частям для определенного интеграла?

5) Запишите формулу замены переменной в определенном интеграле.

6) Что называется криволинейной трапецией?

7) Чему равна площадь криволинейной трапеции?

8) Как найти площадь произвольной фигуры D ?

9) Запишите формулу для вычисления объема тела, полученного от вращения криволинейной трапеции D : y = 0 , x = a , x = b , y = y(x) вокруг оси

Ox .

10) Запишите формулу для вычисления объема тела, полученного от враще-
ния плоской	фигуры	D :	x = a, x =b, y = y1	(x), y = y2 (x),
y1 (x)≤ y2 (x),	x [a,b] вокруг оси Ox .

11)Сформулируйте определение несобственного интеграла с бесконечным верхним пределом интегрирования.

12)Какой вид имеет формула Ньютона-Лейбница для вычисления несобственного интеграла?

8.3.Практическое задание для самостоятельной работы

Задание содержит 4 задачи. Каждая задача имеется в 35 вариантах. Номер задачи состоит из двух чисел: первое число – порядковый номер задачи, второе число – номер варианта.

Студент решает ту задачу, номер варианта которой совпадает с его номером по списку в журнале, подставляя значение параметра k =1, 2, 3, ... – сумма последних двух цифр номера группы.

Задача 1.

Найти интеграл ∫ f (x)dx , используя таблицу интегралов, свойства ли-

нейности интегралов и метод непосредственного интегрирования.

Варианты

2xk+1

3x+k

1.1. ∫

−

+ k+1 x dx

;

1.2. ∫

+ sin 2x −

dx ;

cos

k+1

1.3. ∫(kx3

+ 3 xk

− 4cos5x)dx ;

1.4. ∫(4kx + kx−2k

− 3cos 2kx)dx ;

+ kxk+3

− (k +1)ex

+ x2k+1

1.5. ∫

dx ;

1.6. ∫

−

dx ;

4 + x

sin

+ 3xk+2

+ ke2kx

1.7. ∫

dx ;

cos

+ 2sin 3x − x−k

1.9. ∫

dx ;

+ x

1.11. ∫

−

xk+2 + e(k

1)x dx ;

sin

2kx

1.13. ∫

+ 3 x2k−1 −

dx ;

cos

∫

(k+1)x

k +

1.15.

−

dx ;

k2 − x2

1.17. ∫(2kx3k +

xk − 3sin 2kx)dx ;

1.19. ∫

2kx

−

− k cos 2x dx ;

(x + k )

1.21.

∫

3xk+2 −

+ k+2 x

dx ;

cos2 4x

1.23. ∫

(2kx4 + 3 xk+2 − 5cos 4x)dx ;

1.25.

∫

k +1 −

k + 2

+ x3k

dx ;

9 + x2

∫

+ 3x2k −

1.27.

dx ;

16 − x

1.29. ∫

k + 2

+ 3sin kx − x9−k

dx ;

+ x

1.31. ∫

k + 2

x3k

+ 2ek+x

−

dx ;

sin

1.33. ∫ kxk+2 +

	k +1
1.35. ∫
		2	4x
cos

k +1	− 3sin 2kx dx ;

3 x5k

+ xk3+2 − ke2kx dx .

+ kx3k

∫

1.8.

−

9 − x2

dx ;

1.10. ∫

k − 2cos 2x +

dx ;

1.12. ∫

+ 4k

−

dx ;

k+2

+ x

1.14.

∫

ke−2kx + 2cos

+ 3xk dx ;

1.16. ∫ cos3x − 4

dx ;

sin

∫

xk+1

k + 2

1.18.

− 3e2kx dx

;

k +

1 − x2

− 3 xk +

1.20. ∫ e2kx

dx ;

+ x

1.22. ∫ 5x+2k + sin 4x −

dx ;

k+2

1.24. ∫

+ 3xk+3 − kekx dx ;

sin

k +1

1.26. ∫

+ kxk+3 + 3e3kx dx ;

cos

1.28. ∫(5kx + kx−3k − k cos3kx)dx ;

k +1

1.30.

−3cos kx +

dx ;

k+2

∫

k + 2

1.32. ∫

+ 2k

−

dx ;

k+1

+ x

+ 3x4k

+ e2kx

1.34. ∫

dx ;

sin

Задача 2.

Найти интеграл, применив формулу интегрирования по частям.

2.1. ∫(1 − kx)sin 2xdx ; 2.4. ∫(kx −1)cos 4xdx ; 2.7. ∫(2 − 3x)cos kxdx ; 2.10. ∫(kx −3)cos5xdx;

2.13.∫(x − k )arctg xdx ;

2.15.∫(x − k )ln xdx ;

2.18. ∫xe−kxdx ;

2.21. ∫(2 − kx)e2 dx ; 2.24. ∫xk ln xdx ;

Варианты
2.2. ∫(x + 2)sin kxdx ;	2.3. ∫xcos kxdx ;
2.5. ∫(2 + 3x)sin kxdx ;	2.6. ∫(2x −1)ekxdx ;
2.8. ∫(3 − 4x)sin kxdx ;	2.9. ∫(1 − kx)cos3xdx ;

2.11.∫(kx + 3)cos 2xdx; 2.12. ∫(4 + kx)sin 2xdx ;

2.14.∫(2 − kx)sin 3xdx ;

2.16. ∫(2 − x)cos kxdx ;						2.17. ∫(x + k )ln xdx ;
2.19. ∫(4x −3)sin		x		dx ;		2.20. ∫(kx +1)ln xdx ;

		k
2.22. ∫(1 − 3x)cos		x	dx ;			2.23. ∫(4x + 2)ekxdx ;

	k
2.25. ∫(k −3x)sin		x			dx ;	2.26 ∫(1 − kx)ln xdx ;

5

2.27.∫(5 − kx)e3 dx ;

2.30.∫(1 − 5x)ekxdx ;

2.33. ∫(k − x)e3xdx ;

2.28. ∫(kx +1)sin	x		dx ;		2.29. ∫(kx + 2)ln xdx ;

4
2.31. ∫(1 − kx)cos		x		dx ;	2.32. ∫(kx − 2)ln xdx ;

4					2.35. ∫(1 − kx)cos5xdx
2.34. ∫(x +1)sin kxdx .
Задача 3.

Найти интеграл от рациональной дроби.

3.1.	∫	kx −3				dx ;
		(x +1)(x2 + 4)
3.3.	∫	x2 + k			dx ;
		(x + 2)(x −1)	2

3.5.	∫	x2 + 2x − k		dx ;
		(x +1)(x2 +1)

Варианты

3.2.	∫			7x2 − k				dx ;
		(x		−1)(x +1)			2

3.4.	∫			kx −8					dx ;
		(x −1)(x2 + 4)
3.6.	∫		3x + k		dx	;
		x	2	(x −1)

3.7.	∫		2x2			+ kx − 9			dx ;
				x(x2 + 9)
3.9.	∫					kx +1				dx ;
		(x −3)(x2 +1)
3.11. ∫				kx − 2			dx ;
				2
			x	(	x	)
						+1
3.13. ∫				kx + 2				dx ;
			x	2			3
					− 4x +
3.15. ∫				kx −1				dx ;
			x	2			6
					−5x +


3.17. ∫		x2 +8
			dx ;
	x(x2 + 4)
3.19. ∫		kx − 4		dx ;
	x	2
		− 2x −3

3.21.∫ 3(x2 + k)dx ;

xx2 −1

3.23. ∫( x2 )− k dx ; x2 + 4 (x −3)

3.25.∫ kx2 −1 dx ;

x2 (x + 4)

3.27. ∫	2x2 + kx − 2			dx ;
	(x − 2)	2	(x −1)

3.29. ∫	5x − k			dx ;
	(x2 +1)		(x − 4)
3.31. ∫	x2 − kx − 4			dx ;
	(x −1)(x2 + 4)
3.33. ∫	3x2 − kx +11				dx ;
	(x − 2)	(x2 + 9)

3.8.∫2x2 + x − k dx ;

x(x −1)2

3.10. ∫

x2 − kx + 7

dx;

(x − 2)(x +1)

3.12. ∫

2x − k

dx ;

(x − 3)

3.14. ∫

− kx +1

dx ;

(x2 +1)

3.16. ∫

2x2 + 2x + k

dx ;

(x2 + 9)(x + 2)

3.18. ∫

2x2 + k

dx ;

(x − 2)(x −

3.20. ∫

x2 + kx −1

dx ;

(x −1)(x2 + 4)

3.22. ∫

7x + k

dx ;

(x +1)(x2 + 9)

3.24. ∫

2x2 − kx − 2

dx ;

−3x + 2

3.26. ∫

2x + k

dx ;

(x + 3)(x2 +1)

3.28. ∫

− kx + 3 dx ;

2x2

(x + 5)

3.30. ∫

x2 − kx + 4

dx ;

(x +1)(x2 +1)

3.32. ∫

kx −1

dx ;

(x + 2)(x2 +1)

3.34. ∫

kx2

+ 2x −12

dx ;

x(x2 + 4)

3.35. ∫	2x2 − kx + 3
		dx .
	(x +1)(x2 +1)

Задача 4.

Найти интеграл от иррациональной функции ∫R(n xk , m xl , ...)dx методом

замены переменной.

Варианты

4.1. ∫

xdx

;

x (

x + k 3 x )

4.4. ∫

;

(3 x + k2 )6 x

4.7. ∫

;

4 x (

x + k 4 x )

4.10. ∫

;

4 x (

x + k2 )

4.13.

∫

kdx

;

+ k

4.16. ∫

3 x dx

;

x (

x − k 3 x )

4.19. ∫

;

x +

4.22. ∫

;

4 x (

x − k2 )

4.25. ∫

;

3 x2

+ k

4.28. ∫

;

x (

x − k 4 x )

4.31. ∫

3 xdx

;

x (3 x − k x )

4.2. ∫	dx						dx
			;		4.3. ∫				;
	x (5 x3 + k x )
						k (	x + 3)
4.5. ∫	dx			4.6. ∫		dx
		;						;
	x (3 x + k2 )				x (	x + k 4 x )

4.8. ∫

;

4 x (

x + 4k2 )

4.11. ∫

;

x (4 x + k )

4.14. ∫

;

3 x2

− k

4.17. ∫

;

x (6 x − k )

4.20. ∫

;

− k

4.23. ∫

;

x5 (3 x − k2 )

4.26. ∫

;

4 x (

x − 2k )

4.29. ∫

;

(

x − k )(

x +1)

4.32. ∫

;

x (3 x − k2 )

4.9. ∫

;

4 x −1(

x −1 + k2 )

4.12. ∫

;

+1(x − k )

4.15. ∫

;

x +

4.18. ∫

;

4 x (

x −3k )

4.21. ∫

;

x (k2 4 x +1)

4.24. ∫

;

x −

4.27. ∫

;

x − 3

4.30. ∫

;

6 x (3 x − k2 )

4.33. ∫

;

x (

x − 2k 4 x )

4.34. ∫	4	xdx			(x + k )dx
			;	4.35. ∫	x + 3 .
	x (	4 x − k )

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 2021 / 2221 22 > Следующая >>>

Соседние файлы в папке 080100Экономика(МатАнализ и ЛинАлгебра)

#
26.02.2016483.32 Кб42ЗаданияСР_ЛА_080100.pdf
#
26.02.2016690.03 Кб32ЗаданияСР_МА_080100.pdf
#
26.02.2016516.27 Кб44Лекции_Линейная_алгебра.pdf
#
26.02.20161.35 Mб49Лекции_Математический анализ.pdf
#
26.02.201623.29 Mб199Линейная алгебра_080100_заоч_1_курс_экз_паспорт.pdf
#
26.02.2016753.52 Кб48Математика_Словарь терминов.pdf
#
26.02.201620.68 Mб70Математический анализ_080100_заоч_1_курс_экз_паспорт.pdf