1)Или ;

2) Или ;

3) Или

приводятся к интегралам вида или, где- рациональная функция своих аргументов

Тема 2. Определённый интеграл.

К понятию определённого интеграла можно прийти, решая задачу о вычислении площади криволинейной трапеции, т.е. фигуры, заключённой между прямыми ,,и кривой. Число, равное площади криволинейной трапеции, причём площадь той части, которая лежит выше осиберётся со знаком «+», и ниже её – со знаком «» и называетсяопределённым интегралом от функции на отрезке. Определённый интеграл обозначается, где числа,называютсянижним и верхним пределами интегрирования.

Функция , для которой на отрезкесуществует определённый интеграл, называетсяинтегрируемой на этом отрезке. Достаточным условием интегрируемости функции на отрезкеявляется её непрерывность на данном отрезке.

Если функция интегрируема на, то, по определению, полагают,.

Основные свойства определённого интеграла:

1. .

2. .

3. .

4. Если на , то .

5. Если непрерывна на отрезке,- наименьшее,- наибольшее значенияна, то (теорема об оценке определённого интеграла) .

6. Если непрерывна на отрезке, то существует точкатакая, что справедливо равенство (теорема о среднем значении). Число называется при этомсредним значением функции непрерывной на отрезке.

Понятие определённого интеграла тесно связано с понятием неопределённого интеграла (первообразной).

Если функция непрерывна на отрезкеи- одна из её первообразных, то справедливо равенство:

(формула Ньютона-Лейбница).

Следствиями формулы Ньютона-Лейбница являются формулы замены переменной и интегрирования по частям в определённом интеграле.

Если функции инепрерывно дифференцируемы на, то

(формула интегрирования по частям).

Если функция - непрерывно дифференцируема на отрезкеи функциянепрерывна на отрезке, где,(-образ отрезка, т.е. отрезок для которогопри всех), то

(формула замены переменной).

При замене переменной в определённом интеграле в отличие от вычисления неопределённого не нужно возвращаться к исходному аргументу, так как преобразованный определённый интеграл берётся по тому отрезку, по которому изменяется новый аргумент.

При вычислении неопределённого интеграла по умолчанию предполагалось, что первообразная находится на тех промежутках, на которых выполняемые преобразования подынтегральной функции являются тождественными. При вычислении же определённого интеграла первообразная находится на заданном отрезке, поэтому здесь уже необходимо следить за тождественностью выполняемых преобразований.

Геометрические приложения определённого интеграла.

Площадь фигуры (рис.1) ,равна

.

Площадь фигуры (рис.2) ,равна

.

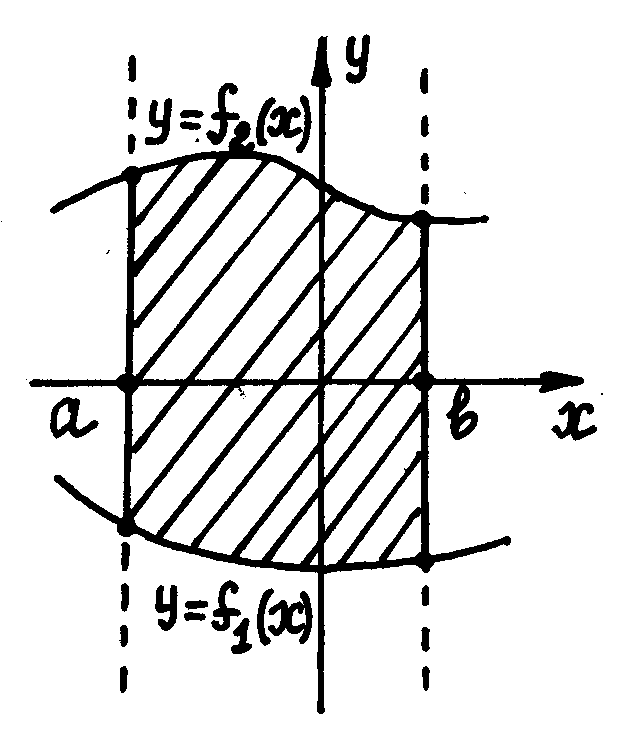
Рис.1 Рис.2

Если фигура (рис.3) ограничена кривой, заданной параметрическими уравнениями ,, прямыми,и осью, то её площадь равна, гдеиопределяются из уравнений,(на отрезке).

Площадь криволинейного сектора (рис.4) ,, где- полярные координаты, равна.

Рис.3 Рис.4

Длина дуги плоской кривой ,равна

.

Длина дуги плоской кривой, заданной параметрическими уравнениями

,,, равна.

Длина дуги пространственной кривой, заданной параметрическими уравнениями ,,,, равна:

.

Длина дуги плоской кривой, заданной в полярных координатах уравнением ,, равна.

Если - площадь сечения тела плоскостью, перпендикулярной к оси, в точке с аппликатой, то объём этого тела равен, гдеи- аппликаты крайних сечений тела.

Объём тела, образованного вращением вокруг оси плоской фигуры (рис.5),равен.

Объём тела, образованного вращением вокруг оси плоской фигуры (рис.6),, равен.

Объём тела, образованного вращением вокруг оси фигуры (рис.7),, равен.

Рис.5 Рис.6 Рис.7