5. Краткие теоретические сведения.

Тема 1. Неопределённый интеграл.

Функция называетсяпервообразной для функции на промежутке, еслидля всех. Функцияможет иметь различные первообразные, но все они отличаются друг от друга только постоянными слагаемыми. Поэтому все первообразные длясодержатся в выражении, где- произвольная постоянная, которое и называетсянеопределённым интегралом от функции и обозначается. Таким образом, по определению.

Операция нахождения первообразной или неопределённого интеграла от функции называетсяинтегрированием этой функции. Функция для которой на промежуткесуществует первообразная или неопределённый интеграл называетсяинтегрируемой на этом промежутке. Первообразная и неопределённый интеграл на промежутке существуют у любой непрерывной на этом промежутке функции. Нахождение неопределённого интеграла состоит в таком преобразовании подынтегрального выражения, чтобы получить интегралы из таблицы основных интегралов (приложение 6.3).

Основные свойства неопределённого интеграла:

1. . 2..

3. ().

4. .

5. Если , то,.

Основными методами интегрирования являются: непосредственное интегрирование, интегрирование заменой переменной и по частям.

Непосредственным интегрированием (интегрированием методом разложения) функции называют отыскание неопределённого интегралас помощью тождественных преобразований подынтегральной функции, свойств3-4 неопределённого интеграла и таблицы основных интегралов.

Часто, заменой переменной интегрирования , удаётся свести нахождение интегралак нахождению более простого интегралас последующей заменой.

Существуют два варианта замены переменной интегрирования:

1) Метод подведения функции под знак дифференциала.

Если подынтегральное выражение может быть записано в виде

, где - дифференцируемая функция, то осуществляется замена. Тогда

.

При подведении функций под знак дифференциала широко используются свойства дифференциалов и таблица дифференциалов основных элементарных функций (приложение 6.3), в частности, преобразования:

; ;

, .

2) Метод подстановки.

Если функция дифференцируема и имеет обратнуюна соответствующем промежутке, то справедливо равенство

.

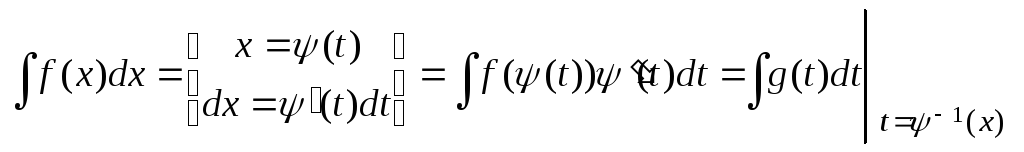Функция подбирается таким образом, чтобы подынтегральное выражение приняло более удобный для интегрирования вид. Выбор её определяется конкретным видом подынтегрального выражения.

Если и- дифференцируемые функции, то справедливаформула интегрирования по частям:

или кратко .

Эта формула используется в тех случаях для вычисления , когда подынтегральное выражениеможно так представить в виде, что интегралможет оказаться проще интеграла.

Этим методом вычисляются: 1) интегралы вида ,

, ,, причём в качествевыбирается;2) интегралы, подынтегральная функция которых содержит в качестве множителя одну из следующих функций: ,,,,,, причём в качествевыбирается одна из указанных выше функций. Указанные группы интегралов не исчерпывают всех без исключения интегралов, берущихся методом интегрирования по частям.