4. Образец решения типовых задач.

1. Найти неопределенные интегралы:

а) ; б); в);

г) ; д); е).

Нахождение неопределённого интеграла состоит в таком преобразовании подынтегрального выражения, чтобы получить интегралы (возможно по новой переменной интегрирования) из таблицы основных интегралов (приложение 6.3).

Решение.

а) Интеграл вычислим непосредственным интегрированием. Получим:

.

б) Интеграл вычислим методом замены переменной интегрирования. Замену переменной интегрирования выполним методом подведения функции под знак дифференциала, используя для этого таблицу дифференциалов основных элементарных функций (Приложение 6.3). Получим:

.

Замечание. Замену переменной интегрирования в данном интеграле можно выполнить и следующим образом. Положим . Тогда, откуда. Подставив все это в интеграл, получим:

Ответ: .

в) Интеграл вычислим методом интегрирования по частям, используя формулу .

Положим: ,. Найдём,

.

Интеграл в формуле интегрирования по частям вычисляется с точностью до постоянной, т.е. в качестве функциивыбирается одна из первообразных для функции.

Для вычисления интеграла можно использовать и следующее свойство неопределённого интеграла: если, то, где- табличный интеграл. В данном случае, так как, то.

Тогда, получим:

Ответ: .

г) Интеграл относится к интегралам вида . Для его вычисления сначала выделим полный квадрат в знаменателе подынтегральной функции, затем сделаем замену переменной интегрирования. Получим:

=[представляем интеграл в виде суммы интегралов].

Вычислим каждый из интегралов в отдельности: 1)

.

Одним из часто выполняемых преобразований является преобразование: , где- некоторые числа.

2)

Тогда:

.

Ответ: .

Конечное выражение для неопределённого интеграла записывают, указывая одну из первообразных и добавляя к ней произвольную постоянную .

д) Интеграл относится к интегралам от рациональных дробей. В данном случае подынтегральная функция является правильной рациональной дробью.

Для вычисления интеграла, сначала разложим дробь на простые дроби: , где неизвестные постоянныенайдем методом неопределенных коэффициентов. Для этого выражение в правой части разложения приведем к общему знаменателю:

и приравняем числители правой и левой дробей. Получим:

Два многочлена одинакового порядка равны, тогда и только тогда, когда равны их коэффициенты при одинаковых степенях .

Приравняв соответствующие коэффициенты этих многочленов, получим систему линейных уравнений относительно :.

Решив систему (например, методоми Гаусса или Крамера), найдем ,,. Тогда.

Затем подставим это разложение в исходный интеграл и используем свойство линейности интегралов.

, где -некоторые числа.

Получим: .

Вычислим теперь каждый из интегралов в отдельности:

1) .

2) .

3) .

Тогда получим: .

Ответ: .

е) Интеграл относится к интегралам вида . Вычисление интеграла сводим методом замены переменной интегрирования к вычислению табличных интегралов от новой переменной, с последующей обратной заменой переменной.

Так как для подынтегральной функции выполняется условие, то сделаем подстановку. Получим:

.

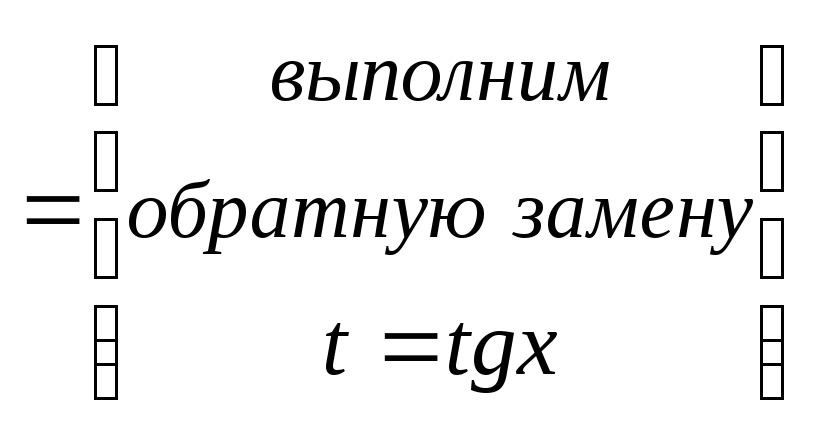
2. Вычислить определённые интегралы: а) б)

Определённый интеграл для функции , непрерывной на отрезке, вычисляют по формуле Ньютона-Лейбница:, где-одна из её первообразных, используя для нахождениявсе приёмы и методы вычисления неопределённых интегралов.

Следствиями формулы Ньютона-Лейбница являются:

1) формула интегрирования по частям , где функцииинепрерывно дифференцируемы на;

2) формула замены переменной интегрирования

, где функция - непрерывно дифференцируема на отрезке. Часто замена переменной в определённом интеграле выполняется с помощью подстановкипо формуле:, где функция- непрерывно дифференцируема на отрезке.

Решение.

а) Первообразная для подынтегральной функции принадлежит к классу первообразных вида. С помощью подстановки(в нашем случае) и формулы замены переменной в определенном интеграле получим:

.

Для вычисления последнего интеграла используем формулу понижения степени: . Тогда

.

б) Первообразная для подынтегральной функции относится к первообразным вида, где- целые числа. С помощью подстановки, где- наименьший общий знаменатель дробей(в нашем случае – подстановки), данный интеграл сводим к интегралу от рациональной функции новой переменной:

.

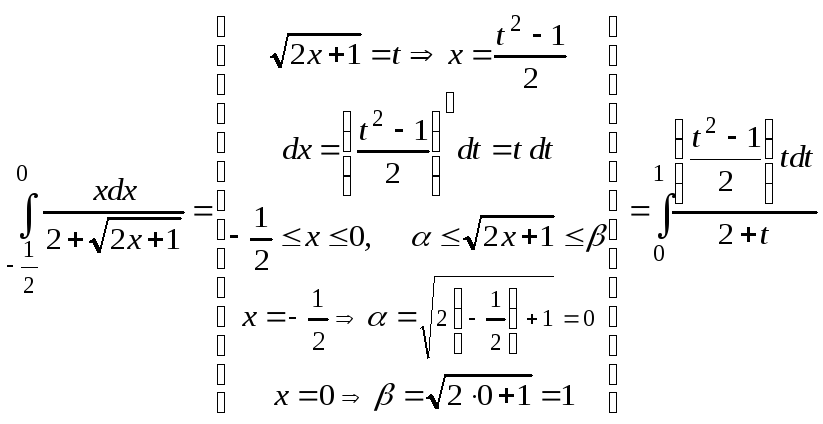
Последний интеграл является интегралом от неправильной рациональной дроби. Для его вычисления, разделим «уголком» числитель на знаменатель и представим подынтегральную функцию в виде:

.

Тогда

.

Для нахождения первообразной вида , где- многочлен порядка, можно использовать также подстановку.

Ответ: а);б) .

3. Вычислить несобственный интеграл I-ого рода или установить его расходимость.

Решение.

По определению несобственного интеграла имеем . Определенный интеграл, стоящий под знаком предела, вычислим методом замены переменной:Тогда.

Ответ: Несобственный интеграл сходится и равен .

4. Вычислить площадь фигуры , ограниченной линиями: ,,,.

Площадь фигуры , где-непрерывные на отрезкефункции, задаваемые одним аналитическим выражением, вычисляется по формуле:.

Площадь фигуры где-непрерывные на отрезкефункции, задаваемые одним аналитическим выражением, вычисляется по формуле:.

Решение.

1) Изобразим фигуру :

2) Представим в виде.

Если или, то фигурупрямыми, параллельными осям координат, разбивают на части, такие, чтобы они имели видили. При этом площадь фигурынаходят как сумму площадей её частей.

3) Вычислим площадь:

.

Ответ: .

5. Вычислить длину дуги кривой, заданной уравнением: ,.

Длина дуги кривой, заданной уравнением ,вычисляется по формуле.

Решение.

1) Сначала найдём: . Тогда

.

2) Вычислим длину: . Последний интеграл является интегралом от неправильной рациональной дроби. Для его вычисления, разделим «уголком» числитель на знаменатель и представим подынтегральную функциюв виде:. Тогда:

.

Ответ: .

6. Вычислить объём тела, образованного вращением вокруг оси фигуры, ограниченной линиями: ,,,.

Объем тела, образованного вращением вокруг оси фигуры, где- непрерывные на отрезкефункции, задаваемые одним аналитическим выражением, вычисляется по формуле:.

Решение.

1) Изобразим фигуру :

2) Представим в виде.

Если , то фигурупрямыми, параллельными оси, разбиваем на части, такие, чтобы они имели вид. При этом объём тела, образованного вращением фигурынаходим как сумму объёмов тел, образованных вращением её частей.

Так как это сделать невозможно, то фигуру разобьём прямыми,на три части,,, такие чтои представим их в виде:,,. При этом.

3) Вычислим объём тела вращения: . Так как

,

,

то: .

Ответ: .

7. Изменить порядок интегрирования в повторных интегралах (изобразить область интегрирования):

.

Повторным интегралом называют: 1) интеграл вида 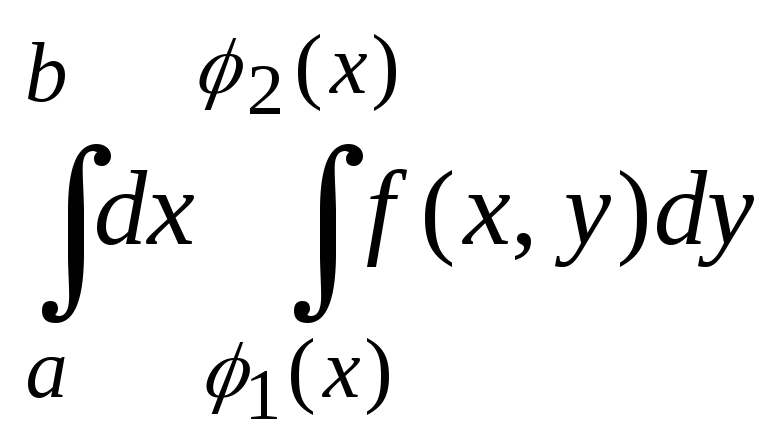по области, называемой элементарной в направлении оси, где-непрерывные на отрезкефункции, задаваемые одним аналитическим выражением;2) интеграл вида по области, называемой элементарной в направлении оси, где-непрерывные на отрезкефункции, задаваемые одним аналитическим выражением.

При изменении порядка интегрирования в повторных интегралах:

1) Если и, то областьпрямыми, параллельными оси, разбивают на части, такие, чтобы. При этом повторный интеграл по областипредставляют в виде суммы повторных интегралов по областям.

2) Если и, то областьпрямыми, параллельными оси, разбивают на части, такие, чтобы. При этом повторный интеграл по областипредставляют в виде суммы повторных интегралов по областям.

Решение.

1) Представим области интегрирования и, являющиеся элементарными в направлении осидля каждого из данных повторных интегралов, в видеи:

, .

2) Изобразим на одном рисунке области интегрирования и.

Очевидно, что .

3) Представим в виде- элементарной области в направлении оси:.

4) Запишем повторный интеграл для функциипо области:

.

Таким образом, изменив порядок интегрирования, получим:

.

Ответ: .

Неявное уравнение окружности с центром в точкеи радиусомпредставляют явными уравнениями:

8. Вычислить двойной интеграл по области , ограниченной линиями:

Если , где- непрерывные на отрезкефункции, задаваемые одним аналитическим выражением, то двойной интеграл вычисляется по формуле. Еслигде-непрерывные на отрезкефункции, задаваемые одним аналитическим выражением, то двойной интеграл вычисляется по формуле.

Решение.

1) Изобразим область интегрирования :

2) Представим в виде:.

Если или, то областьпрямыми, параллельными осям координат, разбивают на части, такие, чтобы они имели видили. При этом двойной интеграл по областинаходят как сумму двойных интегралов по её элементарным частям.

3) Вычислим двойной интеграл:

В повторном интеграле сначала вычислим внутренний интеграл по переменной , считая переменнуюпостоянной величиной:

.

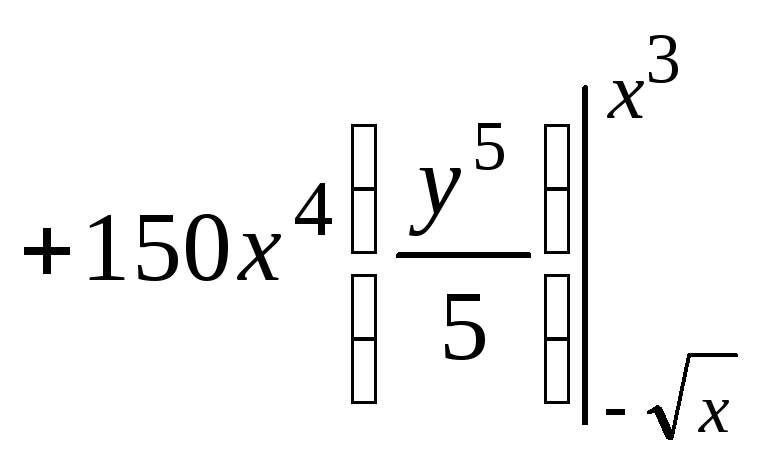
Теперь вычислим внешний интеграл по переменной :

Ответ: 11.

9. Найти среднее значение непрерывной функции в области, ограниченной линиями:.

Среднее значение функциинепрерывной в областинаходится по формуле:, где- площадь области.

Решение.

1) Изобразим область :

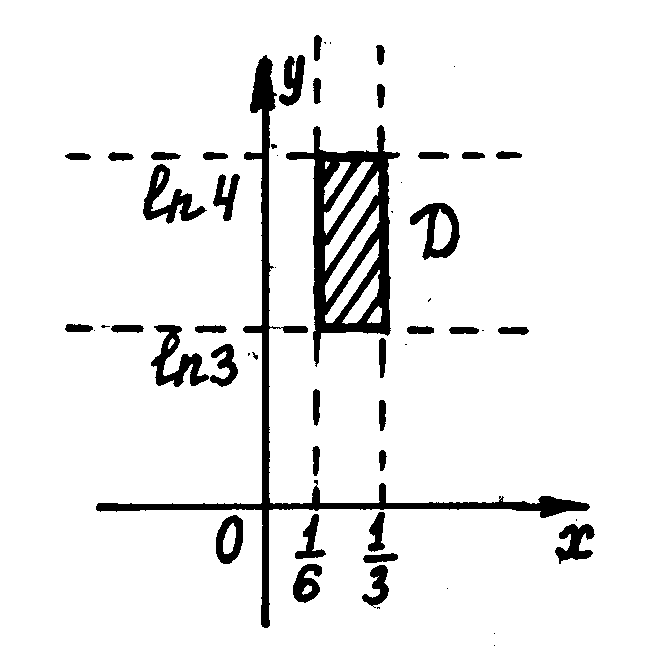
2) Представим в виде:.

Если и, то при выборе формулы для вычисления двойного интеграла через повторный интеграл, следует учитывать вид подынтегральной функциии выбирать такую формулу, для которой вычисления будут наиболее простыми. В данном случае следует выбрать формулу, в которой повторный интеграл записывается для области.

3) Вычислим двойной интеграл :

.

В повторном интеграле сначала вычислим внутренний интеграл по переменной , считая переменнуюпостоянной величиной:

.

Затем вычислим внешний интеграл по переменной :

.

4) Вычислим площадь области :. В повторном интеграле сначала вычислим внутренний интеграл по переменной, считая переменнуюпостоянной величиной: . Затем вычислим внешний интеграл по переменной : Таким образом .

Если область представляет собой классическую фигуру (прямоугольник, треугольник, круг,…), то её площадь можно найти по известным для таких фигур формулам. В данном примере- прямоугольник, площадь которого.

5) Найдём среднее значение функции:

Ответ: .

10. Найти площадь (с помощью двойного интеграла) фигуры , ограниченной линиями: .

Решение.

1) Изобразим фигуру :

2) Представим в виде.

В направлении оси областьэлементарной не является, т.е..

Если и, то фигурупрямыми, параллельными осям координат, разбивают на части, такие, чтобы они имели видили. При этом площадь фигурынаходят как сумму площадей её частей.

С этой целью составим систему уравнений: и найдем ординаты точек пересечения окружности с параболой. Для этого, исключив переменную, получим уравнение относительно переменной:. Решив данное уравнение, найдём. Таким образом:,- ординаты точек пересечения окружности с параболой. Тогда.

3) Вычислим площадь фигуры :.

В повторном интеграле сначала вычислим внутренний интеграл по переменной , считая переменнуюпостоянной величиной:

.

Затем вычислим внешний интеграл по переменной :

.

Так как

;

, то

. Тогда .

Ответ: .

11. Исследовать на сходимость ряды и указать применяемые признаки:

а) ; б); в).

Если общий член числового рядапредставляет собой отношение многочленов или алгебраических функций относительно аргумента, то исследование его на сходимость следует начинать с проверки необходимого признака сходимости. Если он не выполняется, то ряд расходится, в противном случае проводят дополнительное исследование на сходимость, используя предельный признак сравнения, где в качестве ряда сравнения выбирают обобщённый гармонический ряд.

Если в выражение общего члена числового ряда входят:,, то для исследования его на сходимость следует применить признак Даламбера. Если выражение дляможно представить в виде, то для исследования ряда на сходимость следует применить радикальный признак Коши.

Решение.

а) Для данного ряда проверим сначала выполнение необходимого признака сходимости: (если он не выполняется, то ряд расходится). Получим

. Так как необходимый признак сходимости выполняется, то требуется дополнительное исследование ряда на сходимость.

Используем для исследования на сходимость предельный признак сравнения. В качестве ряда сравнения выберем ряд , который сходится, как обобщённый гармонический рядс показателем степени.

При выборе в качестве ряда сравнения обобщённого гармонического ряда руководствуются следующим, если, где- некоторое число, то ряд сравнения имеет вид.

Тогда, по предельному признаку сравнения, так как , то рядыиили одновременно сходятся, или одновременно расходятся. Поскольку рядсходится, то рядтакже сходится.

Ответ: Ряд сходится по предельному признаку сравнения.

При исследовании рядов на сходимость следует иметь в виду следующие предельные значения функций: ,,,,,, а также известные пределы:(),,,,.

б) Данный ряд исследуем на сходимость по признаку Даламбера. Для этого вычислим предел , гдеВ полученном длявыражении выполним преобразование с факториаломи сократим числитель и знаменатель на общие множители. Получим.

Так как , то по признаку Даламбера ряд сходится.

Ответ: Ряд сходится по признаку Даламбера..

в) Данный ряд исследуем на сходимость по радикальному признаку Коши. Для этого вычислим предел , где. С учётом известного предела, получим

. Так как , то по радикальному признаку Коши ряд сходится.

Ответ: Ряд сходится по радикальному признаку Коши.

12. Найти интервал, радиус и область сходимости степенного ряда .

Интервал сходимости степенного рядаобычно находят решая неравенство, где,,- радиус сходимости.

Областью сходимости степенного ряда является интервал сходимости , к которому присоединяются точки, если в них ряд сходится. Для исследования сходимости ряда на концах интервала сходимости обычно применяют признаки сравнения (для рядов с положительными членами) и признак Лейбница (для знакочередующихся рядов).

Решение.

1) Найдём интервал сходимости степенного ряда. Для

этого сначала вычислим предел

. Затем решим неравенство . Полученное неравенство равносильно системе неравенств, откуда:. Таким образом, интервалом сходимости данного ряда является интервал.

2) Радиус сходимости степенного ряда найдём, учитывая, что интервалом его сходимости, где, является интервал, т.е. из условияили. Откуда.

3) Для нахождения области сходимости степенного ряда исследуем его сходимость на концах интервала сходимости , т.е. в точкахи.

При получим знакочередующийся числовой ряд. Исследуем его на сходимость по признаку Лейбница.

Признак Лейбница. Знакочередующийся ряд , где, сходится, если: 1); 2)(может выполняться начиная с номера).

Для этого проверим выполнение условий признака Лейбница:

1) ; 2). Оба условия выполняются и, следовательно, знакочередующийся рядсходится по признаку Лейбница.

При получим числовой ряд, являющийся обобщенным гармоническим рядом с показателем степени. Так как, то этот ряд сходится.

Таким образом, в точках истепенной рядсходится и тогда областью его сходимости является промежуток.

Ответ: Для степенного ряда:- интервал сходимости;- радиус сходимости;- область сходимости.

13. Найти первые три отличные от нуля члена разложения функции в ряд Тейлора в окрестности точки.

Рядом Тейлора функции в точкеназывается степенной ряд

.

Решение.

Найдём сначала первые три отличные от нуля производные функции в точке:,,,. Получим:

;

;

.

Теперь подставим найденные ненулевые значения производных в ряд Тейлора функции в окрестности точкии получим:

.

Ответ: .

14. Разложить в ряд Фурье -периодическую функциюопределённую следующим образом:(в ответе указать первые пять отличные от нуля члена ряда). Построить график функции.

Разложение в ряд Фурье -периодической функции- кусочно-монотонной и непрерывной на промежутке, за исключением конечного числа точек разрыва первого рода, во всякой точке её непрерывности имеет вид:,

где коэффициенты иопределяются формулами:

,;,.

Решение:

1) Найдём коэффициенты ряда Фурье: и:

[для вычисления интегралов применим метод интегрирования по частям]

;

[для вычисления интегралов применим метод интегрирования по частям]

.

Таким образом, получили, что:

, ,.

2) Запишем разложение -периодической функциив ряд Фурье:.

Полученное равенство имеет смысл во всех точках.

Если -периодическая функция имеет точки разрыва 1-го рода, то:

полученное равенство имеет смысл во всех точках, кроме точек её разрыва.

3) Запишем разложение, указав в нём первые пять ненулевых членов ряда Фурье. Для этого вычислим первые пять ненулевых коэффициента ряда Фурье: :,,,,,,,,,,,,,. Таким образом, первыми пятью ненулевыми коэффициентами ряда Фурье являются коэффициенты,,,,и разложение-периодической функциив ряд Фурье имеет вид:.

4) Построим график -периодической функции:

Ответ:

15. Установить тип ДУ первого порядка и найти его общее решение.

а) б)

Решение.

Тип ДУ первого порядка устанавливают по форме его записи.

а) Данное уравнение является дифференциальным уравнением с разделяющимися переменными, так как его можно записать в виде

.

Действительно, осуществив в исходном уравнении замену и умножив его затем на, получим:, т.е. уравнение с разделяющимися переменными.

Нахождение общего решения уравнения, путём деления обеих его частей на, сводится к интегрированию уравнения с разделёнными переменными, где,, общее решение которого записывается в виде.

Разделим обе части уравнения на множитель, получим ДУ с разделёнными переменными:.

Общее решение последнего уравнения найдём интегрированием каждого слагаемого по своей переменной и запишем в виде:

, где - произвольная постоянная.

Общее решение дифференциального уравнения первого порядка должно обязательно содержать одну произвольную постоянную.

Вычислим интегралы (с точностью до постоянного слагаемого):

,

Тогда общее решение дифференциального уравнения запишется в виде:

.

Ответ: , где- произвольная постоянная.

б) Данное уравнение является однородным дифференциальным уравнением первого порядка, так как его можно записать в виде . Действительно, выполнив преобразования:, получим.

При выполнении преобразований однородного ДУ первого порядка к виду следует учесть, что.

Нахождение общего решения однородного ДУ первого порядка с помощью подстановки ,или, где- новая неизвестная функция, сводится к нахождению общего решения ДУ с разделяющимися переменными относительно функциис последующей заменой.

С помощью подстановки ,уравнениеилиприведём к ДУ с разделяющимися переменными видаотносительно новой неизвестной функции. Получим:

.

Последнее уравнение есть уравнение с разделяющимися переменными. Сведём его, разделив обе части уравнения на множитель к уравнению с разделёнными переменными. Получим:

.

Общее решение последнего уравнения найдём интегрированием каждого слагаемого по своей переменной и запишем в виде:

, где - произвольная постоянная.

Вычислим интегралы (с точностью до постоянного слагаемого):

;

.

Тогда общее решение последнего дифференциального уравнения запишется в виде: илив виде:, где- новая произвольная постоянная.

Теперь в найденном решении вернёмся к старой неизвестной функции , выполнив обратную замену. В итоге получим:

или .

Ответ: , где- произвольная постоянная.

16. Установить тип ДУ, найти его общее и частное решения, если:

, .

Решение.

Данное уравнение является линейным дифференциальным уравнением (ЛДУ) первого порядка, так как его можно записать в виде , где,.

Общее решение ЛДУ первого порядка находится с помощью подстановки , где,- новые неизвестные функции. Одну из них, например, находят в виде, где- какая-нибудь первообразная для функции, тогда другую неизвестную функциюнаходят в виде общего решения ДУ:. В итоге будет найдено и общее решение исходного уравнения в виде

Частное решение ДУ, удовлетворяющее начальному условию получают из общего решения данного уравнения при конкретном значении произвольной постоянной. Находяткак решение уравнения, получаемого подстановкой в общее решение начального условия.

Сначала найдем общее решение линейного ДУ первого порядка. Его ищем в виде , гдеи- новые неизвестные функции.

Функцию найдём в виде, где- какая-нибудь первообразная для функции. Вычислив интеграл, получим. Тогда.

Простейшим ДУ первого порядка называется уравнение вида . Общее решение такого уравнения находится интегрированием и записывается в виде.

Функцию найдём как общее решение ДУ:, где,. Данное уравнениеявляется простейшим ДУ первого порядка. Его общее решение найдём интегрированием и запишем в виде. Вычислив интеграл (с точностью до постоянной), получим:

.

Таким образом .

Тогда общее решение исходного уравнения запишется в виде:

.

Теперь найдём частное решение, удовлетворяющее начальному условию .Его получим из общего решения при конкретном значении произвольной постоянной, которое найдём из уравнения, полученного подстановкой начального условия в общее решение. В результате получим: . Тогда частное решение исходного дифференциального уравнения, удовлетворяющее начальному условию, запишется в виде:

.

Ответ: - общее решение;частное решение.

17. Требуется найти:

а) общее решение простейшего ДУ порядка : ;

б) общее и частное решения однородного линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами:

, ,.

Решение.

Общее решение простейшего ДУ -го порядканаходят, выполняя последовательноинтегрирований, и записывают в виде:

.

Общее решение дифференциального уравнения порядка должно обязательно содержатьразных произвольных постоянных.

а) Данное уравнение дважды проинтегрируем.

После первого интегрирования получим: . Интеграл вычислим (с точностью до постоянного слагаемого) методом интегрирования по частям. Получим:

. Тогда .

После второго интегрирования получим: .

Вычислим интегралы (с точностью до постоянного слагаемого). Получим:

;

; .

Тогда

.

Ответ: .

Общее решение однородного линейного ДУ второго порядка с постоянными коэффициентами имеет вид, где- фундаментальная система его частных решений;-произвольные постоянные.

Фундаментальная система решений строится на основе характера корней характеристического уравнения . А именно:1) если - пара различных действительных корней характеристического уравнения, то ФСР имеет вид;2) если - пара одинаковыхдействительных корней, то ФСР имеет вид;3) если - пара комплексно-сопряжённых корней, то ФСР имеет вид.

Корни характеристического уравнения , являющегося квадратным, находят на множестве комплексных чисел по формулам:

1) если дискриминант уравнения , то;

2) если дискриминант уравнения , то.

б) Сначала найдём общее решение ДУ в виде: , где- фундаментальная система его частных решений.

Для нахождения ФСР, составим характеристическое уравнение для данного дифференциального уравнения и найдём его корни на множестве комплексных чисел. Так как дискриминант, то,, т.е. характеристическое уравнение имеет два различных действительных корня. Следовательно, ФСР имеет вид.

Тогда общее решение данного ДУ запишется в виде:.

Теперь найдём частное решение данного ДУ, удовлетворяющее начальным условиям: ,. Для этого сначала найдём производнуюобщего решения:. Затем подставим начальные данные в выражения для общего решения и его производной, получим систему линейных алгебраических уравнений для определения значений произвольных постоянныхи:

.

Решив систему, найдём: ,. Тогда частное решение данного ДУ запишется в виде:.

Ответ:

Общее решение: ; частное решение:.

18. Требуется найти:

а) общее решение линейного ДУ 2-го порядка с постоянными коэффициентами и правой частью специального вида: ;

б) общее решение ДУ 2-го порядка с постоянными коэффициентами и правой частью специального вида (с точностью до неизвестных постоянных в частном решении): .

Общее решение неоднородного ЛДУ 2-го порядка имеет вид, где- общее решение соответствующего однородного уравнения,- какое-нибудь частное решение данного неоднородного уравнения.

Частное решение уравнения с правой частью специального видаищетсяметодом неопределённых коэффициентов в виде , где, если числоне является корнем характеристического уравнения, иравно кратности корняв противном случае;и- полные многочлены степенис неопределёнными коэффициентами. Примерами полных многочленов с неопределёнными коэффициентами степенисоответственно являются:,,,,…. Для нахождения коэффициентов многочленови, надо подставить решениев неоднородное дифференциальное уравнение и приравнять коэффициенты при подобных членах в левой и правой частях полученного равенства. В результате получим систему уравнений, решив которую, найдём значения коэффициентов.

Частное решение неоднородного ЛДУ с правой частьюравно сумме частных решенийнеоднородных уравнений с той же левой частью и правыми частями(принцип наложения решений).

Решение.

а) Общее решение данного ДУ найдём в виде: , где- фундаментальная система частных решений соответствующего ему однородного ДУ: ;- какое-нибудь частное решение данного неоднородного дифференциального уравнения.

Сначала найдём ФСР соответствующего однородного ДУ . Для этого составим характеристическое уравнение для данного однородного дифференциального уравнения и найдём его корни на множестве комплексных чисел. Так как дискриминант, то,, т.е. характеристическое уравнение имеет два одинаковых действительных корня. Следовательно, ФСР имеет вид.

Затем найдём частное решение неоднородного уравнения ,имеющего правую часть специального вида , где,,,. Частное решение найдём в виде, где, если числоне является корнем характеристического уравнения, иравно кратности корняв противном случае;и- полные многочлены степенис неопределёнными коэффициентами. В данном случае: 1) числоне является корнем характеристического уравнения, поэтому; 2), поэтому,, где- неизвестные постоянные, подлежащие определению. Таким образом, частное решение с неизвестными постоянными запишется в виде:

.

Для определения значений постоянных и, найдём производныеи подставим выражения длявместов неоднородное уравнение .Учитывая, что:

, ,

получим:

.

Приравняв, в правой и левой части полученного равенства, постоянные коэффициенты, стоящие при одинаковых функциях, получим систему линейных алгебраических уравнений относительно неизвестных и:. Решив систему, найдём:,. Частное решениезапишется тогда в виде:.

Теперь запишем общее решение исходного уравнения в виде:

.

Ответ: .

б) Общее решение данного ДУ найдём в виде: , где- фундаментальная система частных решений соответствующего ему однородного ДУ: ; -какое-нибудь частное решение данного неоднородного дифференциального уравнения.

Сначала найдём ФСР соответствующего однородного ДУ . Для этого составим характеристическое уравнение для данного однородного дифференциального уравнения и найдём его корни на множестве комплексных чисел. Так как дискриминант, то, т.е. характеристическое уравнение имеет два комплексно-сопряжённых корня, где,. Следовательно, ФСР имеет вид.

Затем найдём частное решение неоднородного уравнения с правой частью .В данном случае функция не является функцией специального вида, но представляет собой сумму функций и, каждая из которых уже имеет специальный вид. Поэтому, используя принцип наложения решений, частное решениенеоднородного ДУ с правой частьюнайдём в виде суммы частных решенийнеоднородных уравнений с той же левой частью и правыми частями.

Сначала найдём частное решение неоднородного уравнения ,имеющего правую часть специального вида , где,,,. Частное решениенайдём тогда в виде, где, если числоне является корнем характеристического уравнения, иравно кратности корняв противном случае;и- полные многочлены степенис неопределёнными коэффициентами. В данном случае: 1) числоявляется корнем характеристического уравнения кратности 1, поэтому; 2), поэтому,, где- некоторые постоянные. Таким образом, частное решениес неизвестными постоянными запишется в виде:.

.

Теперь найдём частное решение неоднородного уравнения ,имеющего правую часть специального вида , где,,,. Частное решениенайдём тогда в виде, где, если числоне является корнем характеристического уравнения, иравно кратности корняв противном случае;и- полные многочлены степенис неопределёнными коэффициентами. В данном случае: 1) числоне является корнем характеристического уравнения, поэтому; 2), поэтому,, где- некоторые постоянные. Таким образом, частное решениес неизвестными постоянными запишется в виде:

.

Общее решение исходного уравнения запишется тогда (с точностью до неизвестных постоянных в частном решении) в виде:

.

Ответ:

.

19. Найти общее решение разностного уравнения:

Общее решение неоднородного разностного уравнения 2-го порядка имеет вид, где- общее решение соответствующего однородного уравнения;- какое-нибудь частное решение данного неоднородного уравнения;- фундаментальная система частных решений (ФСР) однородного уравнения;- произвольные постоянные.

Фундаментальная система решений строится на основе характера корней характеристического уравнения . А именно:1) если - пара различных действительных корней характеристического уравнения, то ФСР имеет вид;2) если - пара одинаковыхдействительных корней, то ФСР имеет вид;3) если -пара комплексно-сопряжённых корней, то ФСР имеет вид, где;.

Частное решение разностного уравнения с правой частью специального видаищется в виде, где, если число, для которогои, не является корнем характеристического уравнения, иравно кратности корняв противном случае;и- полные многочлены степенис неопределёнными коэффициентами. Примерами полных многочленов с неопределёнными коэффициентами степенисоответственно являются:,,….. Для нахождения коэффициентов многочленови, надо подставить решениев неоднородное разностное уравнение и приравнять коэффициенты при подобных членах в левой и правой частях полученного равенства. В результате получим систему уравнений, решив которую, найдём значения коэффициентов.

Решение.

а) Общее решение данного разностного уравнения найдём в виде: , где- фундаментальная система частных решений соответствующего ему однородного разностного уравнения ;- какое-нибудь частное решение данного неоднородного разностного уравнения.

Сначала найдём ФСР соответствующего однородного РУ . Для этого составим характеристическое уравнение для данного однородного разностного уравнения и найдём его корни на множестве комплексных чисел. Так как дискриминант, то,, т.е. характеристическое уравнение имеет два различных действительных корня. Следовательно, ФСР имеет вид.

Затем найдём частное решение неоднородного уравнения ,имеющего правую часть специального вида , где,,,. Частное решение найдём в виде, где, если число, для которогои, не является корнем характеристического уравнения, иравно кратности корняв противном случае;и- полные многочлены степенис неопределёнными коэффициентами. В данном случае: 1) число, для которогои, является корнем характеристического уравнения кратности 1 (это число совпадает с корнем характеристического уравнения кратности 1:, для которого,), поэтому; 2) , поэтому ,, где- неизвестные постоянные, подлежащие определению. Таким образом, частное решение с неизвестными постоянными запишется в виде:.

Для определения значения постоянной , найдёми подставим выражения длявместов неоднородное разностное уравнение .Учитывая, что: ,

,

получим:.

Приравняв, в правой и левой части полученного равенства, постоянные коэффициенты, стоящие при одинаковых функциях, получим уравнение относительно неизвестной :. Решив уравнение, найдём:. Частное решениезапишется тогда в виде:.

Теперь запишем общее решение исходного уравнения в виде:

.

Ответ:.

20. Для заданных функций спроса и предложения на некоторый товар, найти зависимость равновесной цены от времени, если в начальный момент временицена. Является ли равновесная цена устойчивой?

Равновесной ценой на некоторый товар называют цену для которой спрос и предложение на данный товар равны, т.е.. Равновесная цена является устойчивой, если существует.

Решение.

1) Найдём зависимость , такую что. Для этого приравняеми. Получим:

.

Таким образом, равновесная цена , такая что, является частным решением дифференциального уравнения при начальном условии .

Полученное дифференциальное уравнение является ДУ первого порядка с разделяющимися переменными, так как его можно записать, с учётом того, что , в виде.

Сначала найдём общее решение данного ДУ, как уравнения с разделяющимися переменными. Получим:

, где -произвольные постоянные.

Теперь найдём для данного ДУ частное решение, удовлетворяющее начальному условию: . Для этого подставим начальные данные в общее решение и получим уравнение для определения:

Решив последнее уравнение, найдём:. Тогда частное решение ДУ, удовлетворяющее начальному условию:, запишется в виде:

. Полученное решение и является равновесной ценой, такой, что .

2) Выясним, является ли равновесная цена устойчивой? Для этого вычислим предел . Получим: . Так как выполняется условие, то равновесная цена является устойчивой.

Ответ:-устойчивая равновесная цена, такая, что.

21. Для заданных функций спроса и предложения на некоторый товар, найти зависимость равновесной цены от времени, если в начальный момент времени:,. Является ли равновесная ценаустойчивой?

Решение.

1) Найдём зависимость , такую что,. Для этого приравняеми. Получим:

.

Таким образом, равновесная цена , такая что,, является частным решением дифференциального уравнения при начальных условиях ,.

Полученное дифференциальное уравнение является неоднородным линейным ДУ 2-го порядка с постоянными коэффициентами.

Сначала найдём общее решение данного ДУ в виде: , где- фундаментальная система частных решений соответствующего ему однородного ДУ:; -какое-нибудь частное решение данного неоднородного уравнения.

Для нахождения ФСР , составим характеристическое уравнениедля данного однородного дифференциального уравнения и найдём его корни на множестве комплексных чисел. Так как дискриминант, то ,, т.е. характеристическое уравнение имеет два различных действительных корня. Следовательно, ФСР имеет вид.

Частное решение неоднородного уравнения ,имеющего правую часть специального вида (здесь,,,), найдём в виде, где, если числоне является корнем характеристического уравнения, иравно кратности корняв противном случае;и- полные многочлены степенис неопределёнными коэффициентами. В данном случае: 1) числоне является корнем характеристического уравнения, поэтому; 2), поэтому,, где- неизвестные постоянные, подлежащие определению. Таким образом, частное решение с неизвестными постоянными запишется в виде:

.

Для определения значения постоянной , найдём производныеи подставим выражения длявместов неоднородное уравнение .Учитывая, что: ,, получим:. Откуда.

Частное решение запишется тогда в виде:, а общее решение исходного дифференциального уравнения в виде:

.

Теперь найдём частное решение данного ДУ, удовлетворяющее начальным условиям: ,. Для этого сначала найдём производнуюобщего решения:. Затем подставим начальные данные в выражения для общего решения и его производной, получим систему линейных алгебраических уравнений для определения значений произвольных постоянныхи:

.

Решив систему, найдём: ,. Тогда частное решение данного ДУ, удовлетворяющее начальным условиям:,, запишется в виде:. Полученное решение и является равновесной ценой, такой, что,.

2) Выясним, является ли равновесная цена устойчивой? Для этого вычислим предел . Получим: . Так как, то равновесная цена является устойчивой.

Ответ: - устойчивая равновесная цена, такая, что,.