18.7. Производная по направлению. Градиент

Производной функции в точке по направлению называется предел

где

если предел существует.

Если функция дифференцируема, то производная по направлению вычисляется по формуле

(18.31)

где – направляющие косинусы вектора

В частности, если – функция двух переменных, то формула (18.31) производной по направлению примет вид:

(18.32)

где – угол между вектороми осьюОх.

Градиентомфункциив точкеназывается вектор

(18.33)

или, то же самое,

Связь между градиентом функции и производной по направлению устанавливает формула

где – угол между векторамии

Градиент функции указывает направление наибыстрейшего возрастания функции. Наибольшее значение производной достигаемое в направление градиента, равно

В частности, если – функция двух переменных, то

Пример 1. Найти производную функции в точкепо направлению вектораобразующего с положительным направлением осиОх угол

Решение. Используя формулу (18.32), вычислим частные производные функции z в точке A:

Так как то

Пример 2. Найти производную функции в точкепо направлению к точке

Решение. Найдем вектор

Его направляющие косинусы равны:

Найдем значения частных производных функции u в точке

Тогда по формуле (18.31) получим:

Пример 3. Найти длину и направление (указать направляющие косинусы) градиента функции в точке

Решение. Вычислим частные производные функции u в точке М.

Используем формулу (18.33) при условии, что частные производные вычисляем в заданной точке

Тогда

Вычисляем длину полученного вектора:

Используем тот факт, что направляющие косинуса равны координатам единичного вектора направления, определяемого вектором дроби. Поэтому

Задания

I уровень

1.1.Найдите производную функциив точкепо направлению вектора

1)

2)

3)

4)

1.2.Найдите производную функциив точкепо направлению вектора

1.3.Найдите величину и направление градиента функциив точке

1)

2)

3)

4)

5)

II уровень

2.1.Найдите производную указанной функции в точкепо направлению к точке

1)

2)

3)

4)

2.2.Найдите величину и направление градиента функциизаданной неявно, в точке

1)

2)

3)

4)

2.3.Найдите угол между градиентами функциив точкахи

2.4.Найдите производную функциив точкев направленииперпендикулярном к линии уровня, проходящей через эту точку.

III уровень

3.1. Найдите градиент функциив точкахи

3.2.Определите, в каких точках градиент функцииудовлетворяет условию:

1) параллелен оси Оу;

2) перпендикулярен оси Оу;

3) равен нулю.

3.3.Выясните, в каких точках градиент функцииудовлетворяет условию:

1) перпендикулярен прямой 2) равен нулю.

3.4.Определите, в каких точках выполнено равенствоесли

3.5.Найдите градиент функциизаданной неявно уравнением:

1) 2)3)

3.6.Определите направление наибыстрейшего возрастания функции:

1) 2)

3) 4)

18.8. Экстремумы функций двух переменных

Функция имеет в точкелокальный максимум (минимум), если существует такая-окрестность точкиМ₀, что для всех точекиз этой окрестности (отличных отМ₀) выполняется неравенство

Максимум и минимум функции называются ее экстремумами(локальными), а точкаМ₀, в которой достигается экстремум, называетсяточкой экстремума.

Необходимое условие экстремума: если в точке дифференцируемая функцияимеет экстремум, то ее частные производные в этой точке равны нулю:

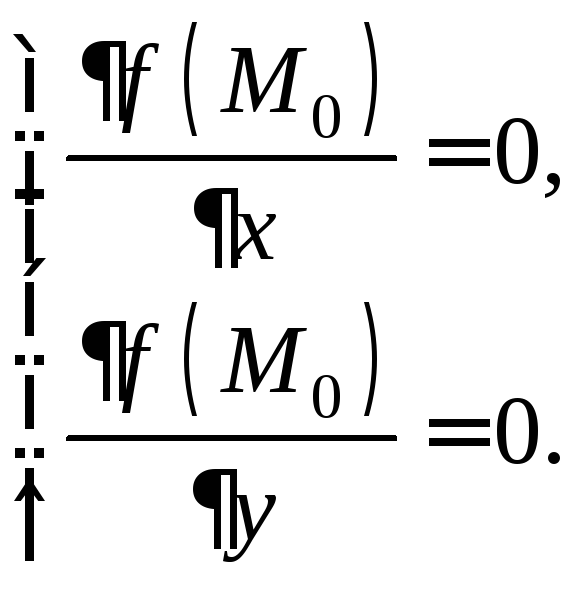(18.34)

Точки, в которых частные производные существуют и равны нулю, называются стационарными.

Точки из области определения функции, в которых частные производные равны нулю или не существуют, называются критическими точками.

Не всякая критическая точка является точкой экстремума.

Достаточное условие экстремума. Пусть– стационарная точка дважды непрерывно дифференцируемой функцииОбозначим:

Тогда:

1) если то функция имеет в точкеМ₀локальный экстремум (максимум прии минимум при);

2) если то в точкеМ₀функция не имеет экстремума;

3) если то в точкеМ₀функция может иметь локальный экстремум, а может и не иметь его (нужны дополнительные исследования).

Допустим, что функция f(x;y) определена на некотором множестве

Число Сназываютнаибольшим значением функции(глобальный максимум) на множестве D, если

записывают так:

Число сназываютнаименьшим значением функции(глобальным минимумом) на множествеD, если

записывают так:

Теорема Вейерштрасса. Непрерывная на замкнутом ограниченном множествефункциядостигает на этом множестве своего наибольшего и наименьшего значений.

Для нахождения наибольшего и наименьшего значений функции в области нужно:

1) найти критические точки функции, принадлежащие D, и вычислить значение функции в них;

2) найти наибольшее и наименьшее значения функции на границах области

3) сравнить все полученные значения функции и выбрать из них наибольшее и наименьшее.

Если область определения функции не является замкнутой, то для нахождения наибольшего и наименьшего значений функции необходимо:

1) найти критические точки функции, принадлежащие D;

2) исследовать найденные критические точки на экстремум (локальный);

3) вычислить значения функции в точках локального максимума (минимума) и отобрать среди них наибольшее (наименьшее).

Пример 1. Исследовать на экстремум функцию

Решение. Находим частные производные первого порядка:

Приравниваем их к нулю, чтобы найти стационарные точки:

Решая систему уравнений, получим: т. е.

Вычисляем значения частных производных второго порядка в точке М₀:

Тогда Следовательно, в точкеэкстремума нет.

Пример 2. Найти экстремум функции

Решение. Частные производные первого порядка:

Стационарные точки:

Частные производные второго порядка:

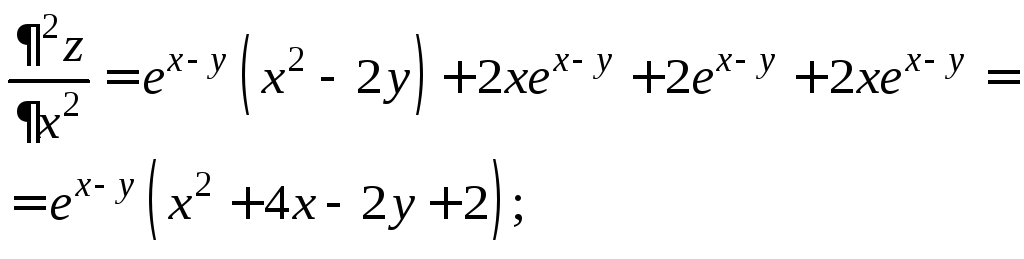
Тогда

Получаем:

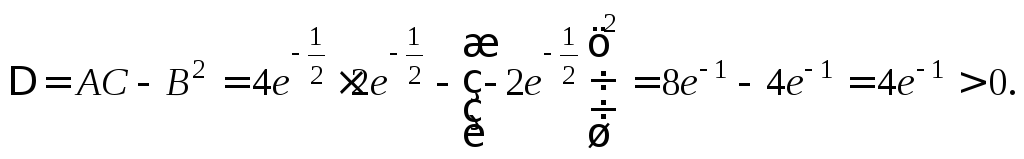
Поскольку то в точкефункция имеет минимум:

Пример 3. Найти наибольшее и наименьшее значения функции в областиограниченной прямыми

Решение. 1) Вычислим частные производные и найдем критические точки:

Получим: – критическая точка, принадлежащая области

Вычислим в ней значение функции:

2) Исследуем функцию z на границе области (рис. 18.4).

Рис. 18.4

Уравнение границы AB: Подставляем число –3 вместох в аналитическое задание функции: где

Исследуем полученную функцию, как функцию одной переменной, на наибольшее значение.

Найдем критические точки:

Получаем – критическая точка, при этом

Вычисляем значение функции в точке и на концах отрезка:

Уравнение границы BC: На этом участке уравнение функции имеет вид:где

Поскольку то дляполучаем критическую точкуТогда

Уравнение границы AC: ТогдагдеКритическая точкапринадлежащая

Вычисляем значение функции для

3) Из всех полученных значений z выбираем наименьшее и наибольшее:

Задания