Предисловие

Особенностью образовательной системы Республики Беларусь является становление и развитие учебных заведений различного типа, в том числе колледжей и высших колледжей. В условиях многоуровневого образования в системе учебных заведений колледж–университет актуальна реализация принципов непрерывности и преемственности в обучении.

Предлагаемое учебное пособие «Математика в примерах и задачах» в 6-ти частях призвано обеспечить процесс изучения математики в высших колледжах и колледжах технического профиля. Оно может быть использовано учащимися на практических занятиях, а также при самостоятельном изучении математики.

При создании настоящего пособия авторы ставили перед собой несколько целей: во-первых, дать значительное количество задач (типовых и оригинальных), которые бы достаточно полно отображали суть основных математических понятий; во-вторых, обеспечить необходимой теоретической информацией для их решений; в-третьих, по каждой теме привести решение основных типов задач; в-четвертых, предлагаемый для решения набор задач распределить по трем уровням сложности. Все эти цели и определили структуру учебного пособия, которое делится на главы, главы – на параграфы. В начале каждого параграфа содержится необходимый справочный материал, затем – решение нескольких задач и набор заданий трех уровней сложности.

Предлагаемая структура учебного пособия, по мнению авторов, делает возможным самостоятельное изучение математики. Его использование позволяет реализовать дифференцированный подход в обучении – каждый учащийся может решать задания доступного ему уровня сложности.

Пособие разработано и прошло апробацию в УО «Минский государственный высший радиотехнический колледж» (МГВРК) в процессе обучения учащихся после базовой школы.

Характерной особенностью методического подхода к изучению математики в МГВРК является построение интегрированного курса математических дисциплин. Этим объясняется то обстоятельство, что определенные темы высшей математики введены в контекст элементарной математики. Поскольку на практике широко реализуется непрерывное образование в системе учебных заведений колледж–университет (в том числе МГВРК интегрирован с Белорусским государственным университетом информатики и радиоэлектроники), то при разработке данного учебного пособия авторы использовали (как и в реальном учебном процессе) в качестве типовых программу изучения математики в средних школах Беларуси и программу изучения высшей математики для высших учебных заведений по специальностям электро-, радиотехники и информатики.

Таким образом реализуются основы непрерывного продолжения обучения в университете. Кроме того, предлагаемое учебное пособие может быть использовано в колледжах при изучении математики по различным базовым и рабочим программам – менее или более полным.

«Математика в примерах и задачах. Часть 3» является непосредственным продолжением учебного пособия «Математика в примерах и задачах. Части 1–2». В этих изданиях принята единая нумерация глав. Предлагаемое пособие (третья часть) состоит из шести глав (гл. 13–18). В отношении авторства отметим, что они подготовлены следующим образом:

М. А. Калугина – гл. 13 «Линейная алгебра», гл. 14 «Векторная алгебра», гл. 15 «Аналитическая геометрия в пространстве»;

Е. В. Уласевич – гл. 16 «Предел и непрерывность функции», гл. 17 «Дифференциальное исчисление»;

Н. В. Михайлова – гл. 18 «Функции многих переменных».

Научно-методическое редактирование осуществила Л. И. Майсеня, она является соавтором всего пособия.

Авторы благодарны рецензентам учебного пособия – доктору физ.-мат. наук, профессору А. В. Метельскому и сотрудникам кафедры высшей математики БГУИР, особенно зав. кафедрой, доктору физ.-мат. наук В. В. Цегельнику и профессору А. А. Карпуку, за очень внимательное прочтение рукописи и ряд ценных замечаний, устранение которых улучшило наше издание.

Надеемся, что предлагаемое издание будет содействовать активизации мыслительной деятельности учащихся и повышению эффективности учебного процесса при изучении математики.

13. Линейная алгебра

13.1. Матрицы и операции над ними

Матрицей называется прямоугольная таблица, составленная из элементов некоторого множества. Горизонтальные ряды такой таблицы называются строками матрицы, а вертикальные – ее столбцами. Матрицы обозначают A, B, C, X… . Запись a_ij используют для указания местоположения элемента матрицы (i – номер строки, j – номер столбца). Числовую матрицу размеров (т. е. состоящую изm строк и n столбцов чисел) в общем случае записывают в виде

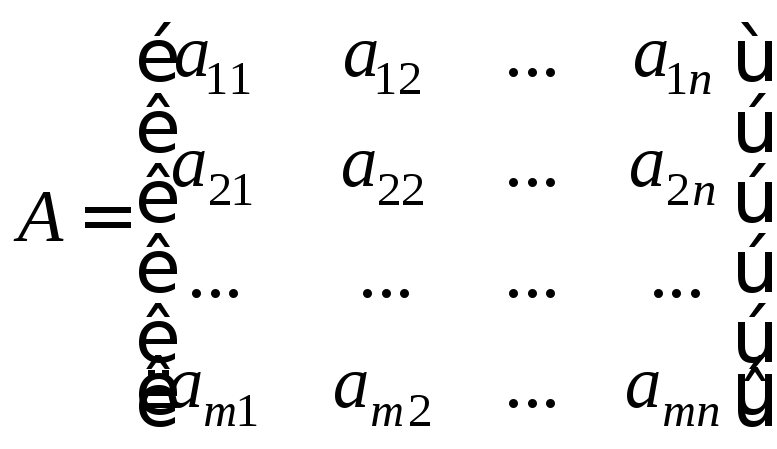
или в более компактной форме

Ее обозначают также

Если m = n матрицу называют квадратной порядка n и обычно обозначают A_n. Элементы a_ii, такой матрицы образуют ее главную диагональ.

Квадратная матрица вида

(13.1)

где называется диагональной. Если для любогото матрица (13.1) называетсяединичной и обозначается E_n.

Верхней и нижней треугольными матрицами называются квадратные матрицы вида

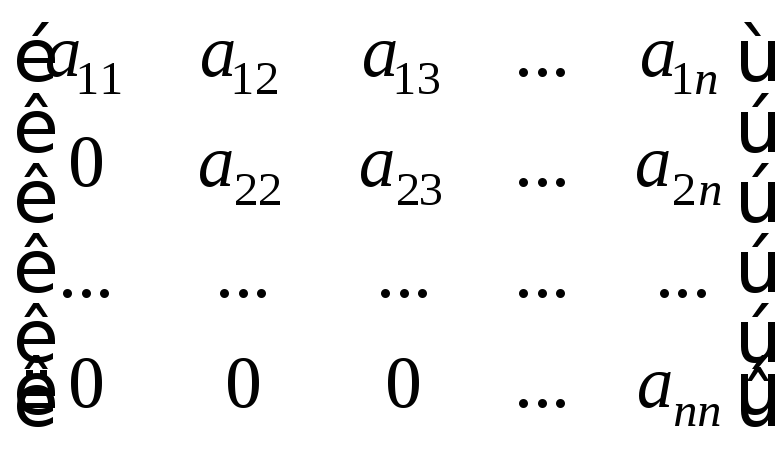и соответственно.

Трапециевидной матрицей называется матрица вида

где числа a₁₁, a₁₂, …, a_kk отличны от нуля.

Нулевой матрицей называется матрица, все элементы которой равны нулю. Обозначают такую матрицу буквой O.

Две матрицы одинакового размера

и (13.2)

называются равными, если для всех

Суммой матриц (13.2) называется матрица A + B размеров m × n, состоящая из элементов где

Произведением матрицы A_m×n на число α называется матрица

Разностью матриц (13.2) называется матрица A – B = A + (–1)B.

Противоположной к В называется матрица –В, такая что

Свойства операций сложения матриц и умножения

на число:

1. 

2. 

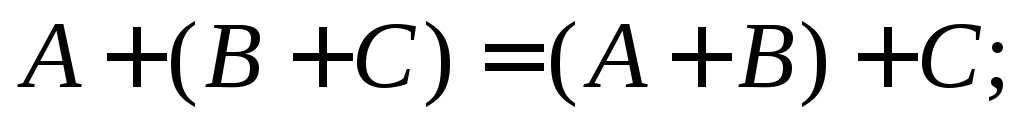
3. A + 0 = А;

4. А + (–А) = 0;

5. 

6. 

7. 

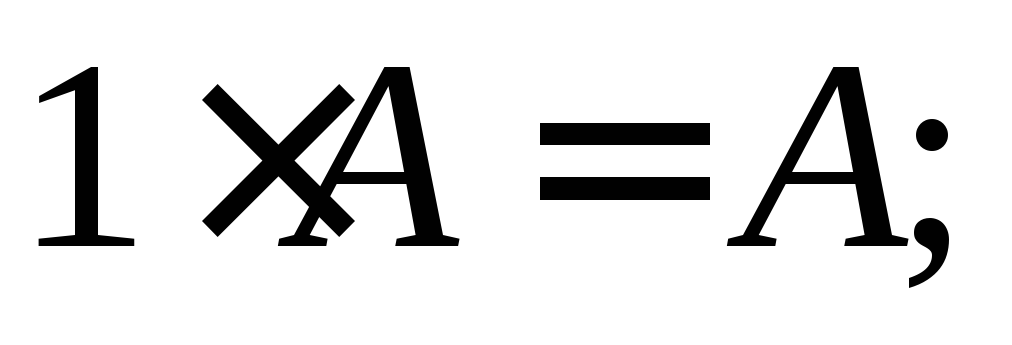
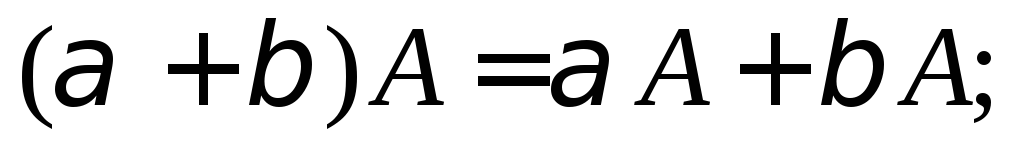
8. а матрицы A, B и С – одинакового размера.

Для матриц A и B может быть введена операция умножения A·B при условии, что матрицы согласованы, т. е. количество столбцов матрицы A равно количеству строк матрицы B.

Произведением матрицы A_l×m на матрицу B_m×n называется матрица элементы которой

Для получения элемента с_ij матрицы С умножают последовательно каждый элемент i-й строки матрицы А на соответствующий элемент j-го столбца матрицы B и находят сумму этих произведений.

Свойства операции умножения матриц

1. 

2. 

3. 

4. 

5. 

6. 

В общем случае из существования AB не следует существование BA. Даже если оба эти произведения определены, они не всегда равны. Матрицы, для которых называютсякоммутативными или перестановочными.

Пусть A – квадратная матрица. Тогда k-я степень () матрицыA определяется равенством По определению принимаютпри условии

Матрица A^T, полученная из матрицы A заменой столбцов строками с теми же номерами, называется транспонированной к матрице A, т. е.

Свойства операции транспонирования матриц

1. 

2. 

3. 

4. 

Если для квадратной матрицы A выполняется соотношение то матрицаA называется симметрической матрицей, а если – токососимметрической.

Элементарными преобразованиями над строками матрицы A называют следующие операции:

1. перестановку строк;

2. умножение строки на ненулевое число;

3. прибавление к элементам строки соответствующих элементов другой строки, умноженных на ненулевое число.

Говорят, что матрица A эквивалентна матрице B (пишут: A~B), если матрица B получена из A при помощи элементарных преобразований строк.

Пример 1. Найти 2A – 3B, если

Решение. Прежде всего следует заметить, что матрицы A и B имеют одинаковый размер 2×3. Поэтому по определению линейных операций над матрицами имеем:

Пример 2. Если возможно, вычислить соответствующие произведения и проверить справедливость равенства AB = BA для следующих пар матриц:

1) 2)

3) 4)

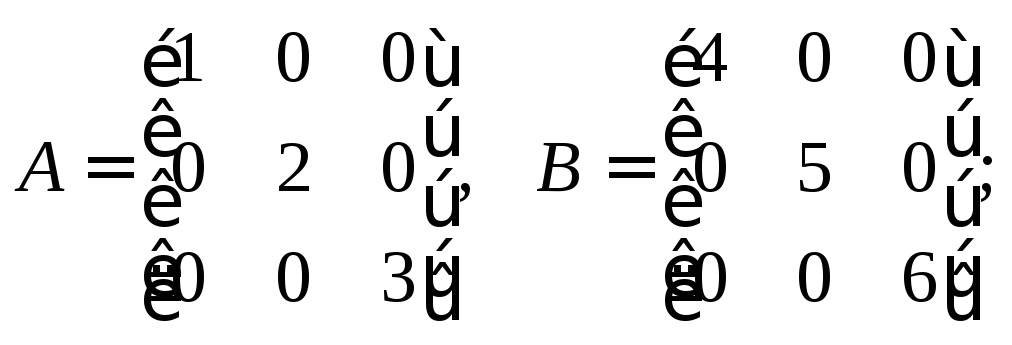
5)

Решение. 1) Матрицы A и B согласованные, так как матрица A имеет размер 2×2, а матрица B – размер 2×3, т. е. количество столбцов матрицы А совпадает с числом строк матрицы B.

Умножение матрицы B на матрицу A невозможно, так как матрицы не согласованы (число 3 столбцов матрицы B не равно числу 2 строк матрицы A).

2) Произведения AB и BA могут быть найдены, так как в обоих случаях матрицы согласованы:

.

Приходим к выводу, что

Приведенный пример иллюстрирует не только отсутствие свойства коммутативности операции умножения для многих согласованных для этого действия матриц, но и показывает, что при умножении двух ненулевых матриц может быть получена нулевая.

3) Матрицы A и B согласованы для умножения, но произведения AB и BA имеют разные размеры и элементы:

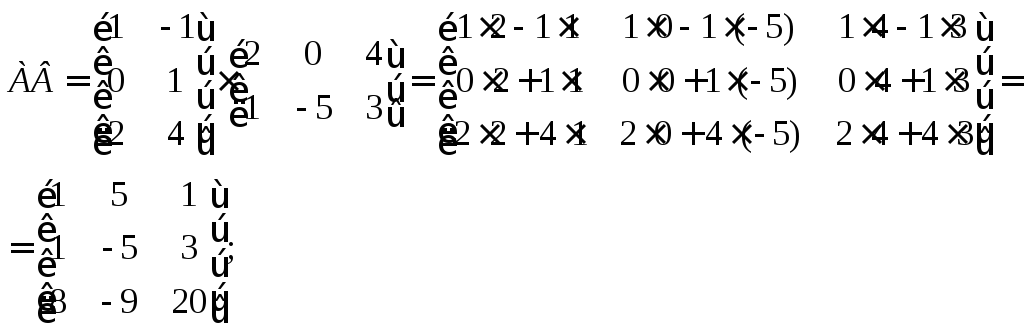
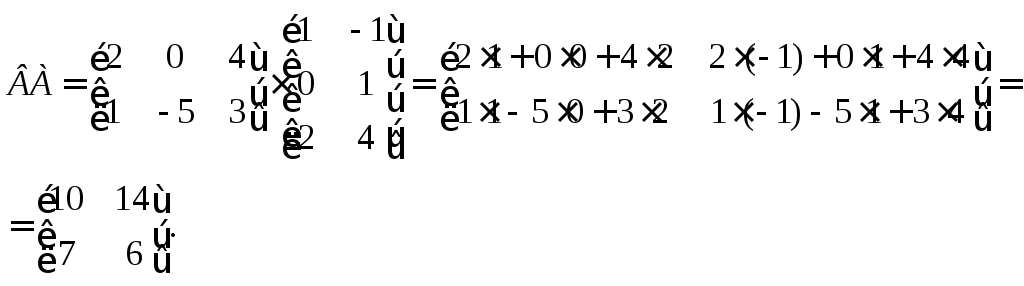
AB и BA – квадратные матрицы размеров 3×3 и 2×2 соответственно,

4)

Приходим к заключению, что

Очевидно, что условие будет соблюдаться для любых диагональных матриц одного размера.

5) Матрицы A и B согласованы для умножения:

при соблюдении условий: т. е. при Таким образом, матрица A является коммутативной с матрицей или где a, b, с – любые действительные числа.

Пример 3. Найти матрицу X, удовлетворяющую условию если известна матрица

Решение. Запишем равенство в видеа затеми, наконец,Посколькуто

Пример 4. Найти значение матричного многочлена f(A), если

Решение. По условию задачи

Пример 5. Привести матрицу А к треугольному виду с помощью элементарных преобразований строк, если

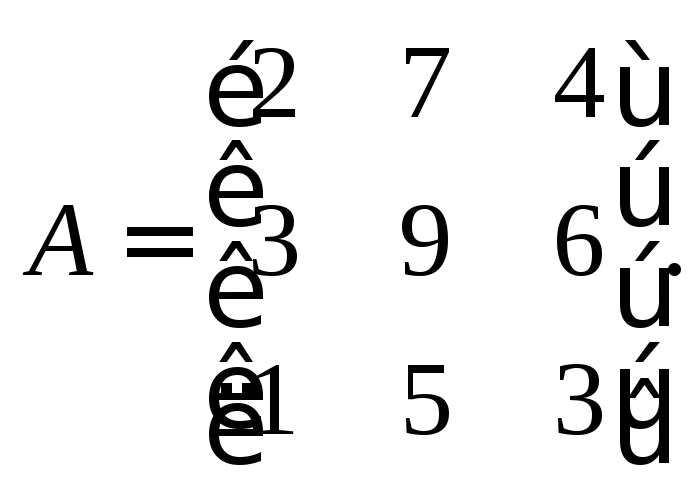
Решение. Поменяв строки местами, получим матрицу, эквивалентную исходной:

Затем запишем вместо второй строки сумму первой, умноженной на (–2), и второй, а вместо третьей – результат сложения первой, умноженной на (–3), и третьей:

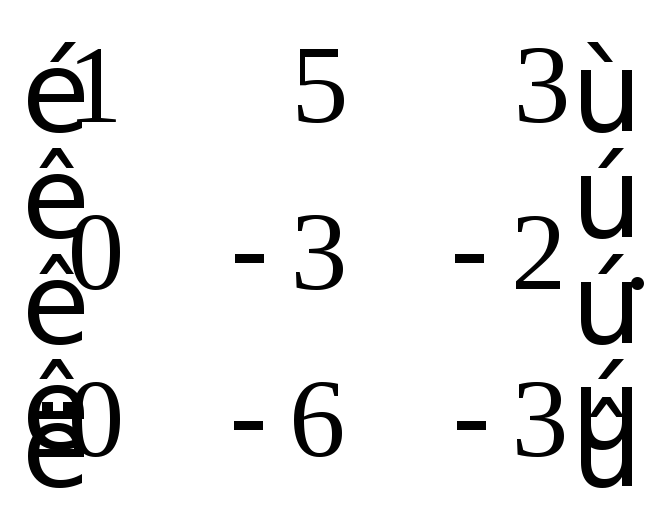
Осталось прибавить к третьей строке вторую, умноженную на (–2):

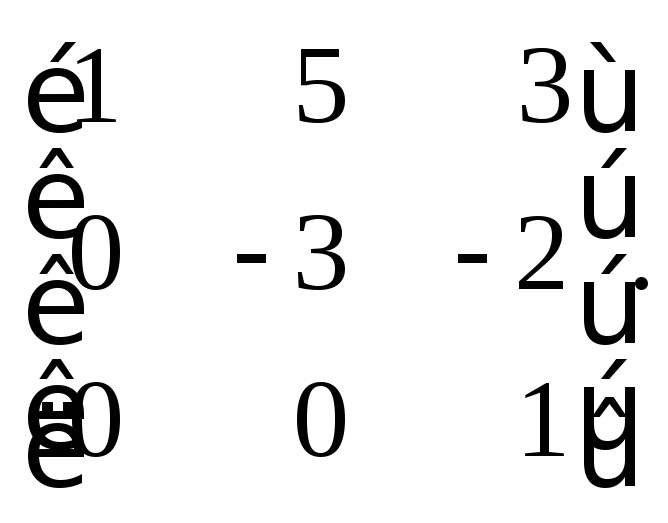
В результате получена треугольная матрица, эквивалентная матрице A.

Эти преобразования (без комментария) записывают в виде

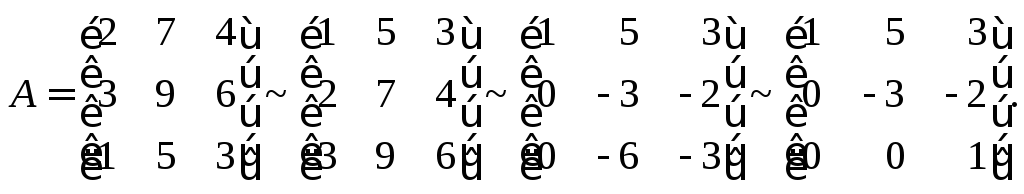
Задания